11.3　重复性和再现性

对于测量系统的分析，最终要得出测量系统是否合格的结论。对于偏倚及稳定性方面的问题，前面两节已分别进行了分析。相对而言，偏倚及稳定性方面的问题比较简单，也容易解决。测量系统不满足要求更容易出问题的地方常常在于精度方面。而提高精度的问题要复杂得多，下面对构成精度的组成部分，即测量系统的重复性与再现性进行仔细分析。

本节中最重要的公式是构成精度的组成公式：

式中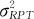，代表重复性方差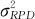；代表再现性方差。

11.3.1　重复性

整个测量系统指的是在测量过程中，由人员、仪器或量具、测量对象、操作方法和环境所构成的整体。测量系统中的各环节都可能出现误差，测量系统的总误差是由各方面误差综合而成。重复性误差指的是同一个操作者使用同一套测量设备，对同一个测量部件的同一特性在较短的时间间隔内进行多次测量，所得结果的一致性。重复性强调所有的测量都是在尽可能相同的条件下完成的，这时误差的产生全部是由测量设备本身的固有波动引起，这部分误差一般是不可能再降低的。因此，重复性又称为设备波动（equipment variation，EV）。如果重复性误差过大，则测量系统无法改进，只能彻底更换。

重复性作为研究测量系统固有波动的度量，除了选用其方差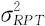作为绝对量的度量指标，也常选用设备波动与过程总波动（total variation，TV）的比值作为其相对量的度量指标，即是重复性标准差与过程总体标准差的比值（这是个无量纲的比率），即

11.3.2　再现性

测量系统的误差不仅包含重复性误差，人员、仪器或量具、操作方法和环境的变化等也都可能形成误差。所谓再现性是指在各种可能变化的测量条件下，对同一个测量部件的同一特性进行多次测量，所得结果的一致性。可能改变的测量条件包括操作者、操作方法、测量设备、测量地点、使用条件和测量时间等。其中相当普遍的情况是，误差主要由不同的操作人员引起。因此，再现性又称为人员波动（appraiser variation，AV）。

再现性作为研究具有多个波动源的测量系统波动的度量，除了选用其方差作为绝对量的度量，也常选用人员波动与过程总波动的比值作为其相对量的度量指标，即是再现性标准差与过程总体标准差的比值（这是个无量纲的比率），即

当然也有这种情况，即在测量系统中不存在人员波动（例如数字式测量仪器）或人员波动小到可以忽略不计。这时，导致误差的应该是另外一些原因，例如不同的测量设备、不同的设置、不同的班次或不同的环境条件等，我们根据测量系统的真实运行状况分析哪些是最主要的再现性误差原因，并以此代替人员波动作为再现性误差的主体。

11.3.3　精确度分析

重复性和再现性分析一同构成了测量系统精确度分析的主要内容，二者应该同时评估，这是测量系统分析的重点。

当重复性方差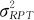以及再现性方差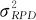都求出后，可以将二者求和，用式（11—8）求出测量系统的精度的平方，然后求出其平方根即为测量结果波动的标准差：

求出σ_MS后，可以进一步求出评价测量系统精确度的两项重要指标：％GageR&R和％P/T。由于重复性和再现性两个英文字皆以R开头，所以习惯上也用R&R表示精度，即R&R＝6σM_S。评估指标％GageR&R是测量系统波动占过程整体波动的百分比，其数学定义公式为：

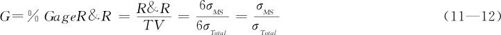
另一个评估指标％P/T则是指测量系统精度占公差的百分比，其数学定义公式为：

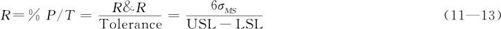
％P/T着重评估测量系统针对相关产品规格的测量效果，强调测量系统对公差界限的分析性能（判断产品是否合格）能否测量得足够精确。％GageR&R着重评估测量系统对整体过程变异的测量效果，强调测量系统对生产过程改进分析性能（过程是否已有改进）能否测量得足够精确。％P/T和％GageR&R是评估测量系统性能的两个不同方面，缺少其中任何一个都将是不全面的。一个好的测量系统，必须同时使这两项指标都足够小。表11—2归纳了这两个度量指标的判断标准。

表11—2　测量系统的合格标志

对于表11—2的理解应该是：

（1）若％GageR&R及％P/T两项指标皆小于10％，则测量系统良好。

（2）若％GageR&R或％P/T两项指标有一项大于30％，则测量系统不合格，不可接受，测量系统必须改进后才能使用。

（3）若处在（1）与（2）之间的情况，则测量系统性能属于边缘状况。当测量系统测量的指标并非产品的关键性能指标，且更换测量系统在经济上不可行时，则测量系统可以勉强使用；否则测量系统也应加以改进才能使用。

对于测量系统精确度的分析还可以从另一个指标“可区分类别数（ndc）”来体现。为此，我们先从统计学角度说明式（11—3）的来源，然后补充说明GageR&R与ndc的关系，对ndc要求的含义，以及GageR&R与P/T两个指标间的联系，并讨论它们与过程能力指数C_p的关系。这段内容中用到数学推导较多，初学者可以先略去不看，只要直接学习测量系统分析的实现方法就够了。

在最开始提出“可区分类别数（ndc）”概念的一本测量分析手册（参见参考文献［24］）中，引用了惠勒和里达伊（Wheeler and Lyday）的专著《评估测量过程》（参见参考文献［31］）的结果。那里先引入判别比（discrimination ratio，DR），然后根据理论上的推导得到作为近似公式的定义（参看参考文献［32］），即可区分类别数（number of distinct categories，ndc）。

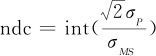
我们希望从统计意义上直接说明此定义的来源。为此，我们先要介绍一个预备知识，即分析两个正态总体均值间有显著差异需要什么条件。下面我们给出重要结论：

预备1：两个有相等方差σ²的均值分别为μ₁和μ₂的正态总体，对于检验问题：

H₀：μ₁＝μ₂H₁：μ₁≠μ₂

假设各抽取相同的样本量n的样本，记二者的样本均值分别为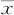和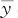，取第一类风险α＝0.0027，则当

时，将拒绝原假设，从而可得出结论，认为两总体均值不相等。

事实上，由本书5.3.2.1节双正态总体均值检验的式（5—13）可知，当两组样本量相等（皆为n）时，式（5—13）变成

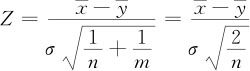
拒绝原假设的区域应该是：

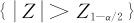
当α＝0.0027，上式右端就是Z_0.99865＝3，拒绝域就简化为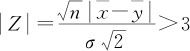，也就是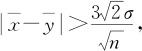预备1证明完毕。

对于通常使用的检验水平α＝0.05，式（11—14）改为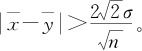

我们下面回到测量系统的可区分类别数的讨论。设生产过程的标准差为σ_P，整个生产过程的波动可以用6σ_P表示，测量系统的精度为σ_MS，当从生产过程中任意抽取能够代表整个变异范围的若干样品（例如100个），用我们现有的测量系统只测量一次，平均说来，能将这些数据分成几组（置信水平99.73％）？

显然，能够分成的组数等于

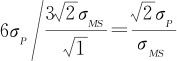
因为此数只能为整数，所以我们得到式（11—3），这里可区分类别数（ndc）为：

式中取整应该是“下取整”（MINITAB用Floor来表示），这就是式（11—3）的由来。

通常的六西格玛教材中都认为：可区分类别数ndc小于5时，测量系统不具备足够的分辨力；当可区分类别数ndc大于等于5时，测量系统具备足够的分辨力；当可区分类别数ndc大于等于10时，测量系统具备优良的分辨力。表11—3对此做了进一步的说明（详细结果可参看MINITAB数据文件“ndc.MTW”，那里分别计算了四舍五入取整和下取整两种方法）。

表11—3　分辨力对过程控制与分析的影响

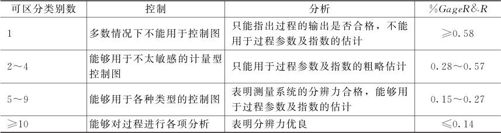
其实，如果坚持“％GageR&R小于0.1测量系统可判优”的标准，换用ndc的结果，标准不应该是“ndc超过10可判优”，而应该是“ndc超过14可判优”才更合理。

例11—2介绍了计算可区分类别数的软件实现方法。

在表11—3中这些对于ndc的要求是怎样得来的？下面给出定量的回答。我们在式（11—12）中已介绍了测量系统精度指标％GageR&R的定义（以下此值用G来表示），即

式中，σ_T是σ_Total的缩写。

下面我们给出可区分类别数ndc与测量系统精度指标％GageR&R的关系式：

式（11—17）的证明：

因为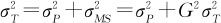，故（1－G²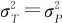），因此，σ_P＝σ_T，将此式代入ndc的定义式（11—15）即可得

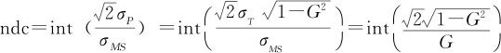
由式（11—17）可见，ndc与％GageR&R与二者完全是一一对应的函数关系，它们完全是一回事，只不过表达方式不同罢了。可区分类别数表11—4列出几个常用的对应关系。

表11—4　ndc与％GageR& R对应关系表

很明显，可区分类别数ndc与％GageR&R二者完全是一回事；而ndc与真正的“分辨力”（仪器仪表的最小刻度）反而完全是两码事。所谓ndc代表“分辨力”，其实是指从测量系统的精确度角度来说明对于描述生产过程变化的分辨能力。

具体实现测量系统分析有两类方法：一类是将测量系统的分析与生产过程的波动结合在一起分析，常称为传统方法；另一类是先不考虑生产过程的波动，只使用标准件或固定件，这可以对测量系统分析得更细致，但只能直接计算％P/T指标，为了计算％GageR&R必须由其他方法获得过程的波动才行，因为这个指标在计算上的关键是要确保对于过程总波动（TV）的度量要准确，要真的能够涵盖整个过程范围。两种方法都很有用，在此先介绍常用的第一类方法。

所谓传统分析方法，是指在过程实际变化范围内选择若干部件（大约10件），再随机选择若干操作员（大约3人），让每个操作员按随机顺序对所有部件重复测量几遍（通常重复2～3次）。收集并整理好所有的测量记录后，可以有三种计算方法：极差法、均值极差法和方差分析法。三者各有特点，其中以方差分析法为最准确，极差法及均值极差法都是早期以手工计算为主时所采用的为了计算简单而使用的，现在已很少使用。这里关键是要理解整个分析的整体思路，特别是重复性和再现性的计算思路，其示意见图11—8。

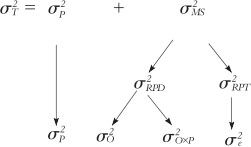
图11—8　测量系统精确度分析的传统方法示意图

事实上，由式（11—1）得知：

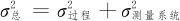
用英文字母表达，则可以写成：

这里观测到的全体波动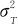，包括了过程实际的波动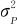和测量系统的波动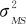。而测量系统的波动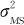又可以写为（见式（11—8））：

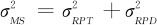
在传统的测量系统分析方法中，同一个测量者测量同一个部件的波动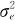本身就构成重复性方差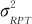，测量者的波动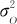以及测量者与部件交互作用的波动构成了再现性波动。因此，最后归纳出下列公式：

如果求出各个方差分量，就可以最终计算出评估测量系统的两项指标。

实际操作时，首先应在过程实际变化范围内选择S个部件，再随机选择R个操作员，让每个操作员按随机顺序对所有部件重复测量T遍，将第r个操作者对第s个部件进行第t次测量的结果记为Xr_st。收集并整理好所有的测量记录，为整个测量系统的计算分析做好准备。容易看出，两个因子（测量员与部件）之间是交叉关系，而且二者都是随机效应因子。根据第10章介绍的方法，应该先计算出方差分析表，然后求出方差分量。

这里，数学模型是：

式中，μ是总均值；O_r，P_s，（OP）r_s和er_st分别是操作者、部件、操作者与部件交互作用和测量误差的随机变量，假设O_r～N（0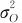，），P_s～N（0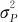，），（OP）_rs～N（0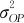，），e_rst～N（0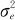，），且四者相互独立。

然后，将离差的总平方和SS_T进行分解，先得到方差分析表（见表11—5）。

表11—5　测量系统的方差分析表

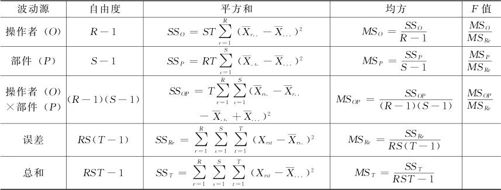
以表11—5为基础，可以根据下列公式进一步计算出各个波动源的方差分量：

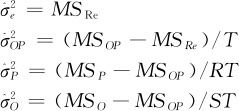
已知σ²_e代表重复性的方差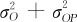，代表再现性的方差，因此测量系统重复性和再现性的标准差为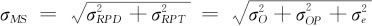，而过程总波动的标准差为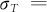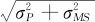，将σ_MS及σ_T以其估计量代入，再加上已知的公差界限Tolerance，就可以分别计算出％GageR&R和％P/T值。

下面用例11—2对测量系统的重复性和再现性的计算过程加以说明。

例11—2

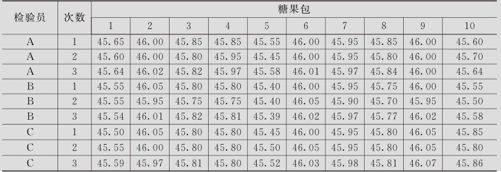
某食品厂生产袋装糖果，用秤测量其重量（单位：千克）。已知公差要求为45.5±0.5。为进行测量系统分析，在总装线终端有代表性地抽取10包成品糖果编好号，随机挑选3位检验员用同一台秤测量每包重量，将糖果包顺序打乱后再测一次，再打乱后测第3次。试做测量系统的精确度分析（数据列在表11—6中，数据文件：QT_MSA重复性与再现性.MTW）。

表11—6　糖果重量的测量结果

解　计算机MINITAB软件对于这种传统数据格式有专门的窗口实现计算：

1．从“统计＞质量工具＞量具研究＞量具R&R研究（交叉）（Stat＞Quality Tools＞Gage Study＞GageR&RStudy（Crossed））”进入。

2．指定“部件号（Part numbers）”为“糖果包”，“操作员（Operators）”为“检验员”，“测量数据（Measurementdata）”为“测量值”，保持“Method of Analysis（分析方法）”为“ANOVA（方差分析）”。

3．选择“选项（Option）”，在“过程公差（Processtolerance）”中的“规格上限—规格下限（Upper spec-Lower spec）”中输入“1.0”。

运行命令后可以得到如图11—9所示的会话窗口输出和如图11—10所示的分析图形。

图11—9　重复性与再现性的分析结果

图11—9显示的主要是波动源方差分析和测量系统能力的计算结果。容易看到重复性方差为0.0010622；检验员方差为0.0008105；检验员与糖果包交互作用方差为0.0026965；后两项求和得到再现性方差为0.0035070；重复性方差与再现性方差求和为0.0045693（此即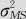）；过程方差为0.0360033；这最后两项求和得到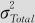＝0.0405726。再经过一些简单运算可得％GageR&R＝33.56％＞30％，％P/T＝40.56％＞30％，可见重复性和再现性的水平都不高。ndc＝3＜5，可见分辨力较弱。总之，测量系统是不合格的，我们必须切实改进该测量系统进行再次评估，然后才能使用。

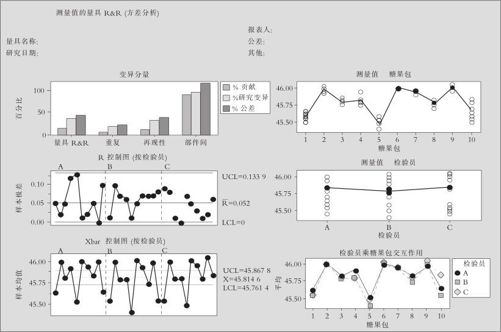
图11—10　重复性与再现性分析图

图11—10是一张六合一的图形。其中左上图是波动源各分量大小的条形图，生动地展示了会话窗口中的计算结果。

百分比贡献条形表示各波动分量的方差与总体波动分量的方差之比，即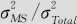；百分比研究变异条形表示各波动分量的标准差与总体波动分量的标准差之比，即σ_MS/σ_Total；百分比公差条形表示各波动分量的标准差的6倍数与公差之比，即6σ_MS/Tolerance。由于％GageR&R指标要小于0.1才合格，分子分母同时平方后可以看出，量具R&R的百分比贡献条形高度要小于1％才合格，也就是说，量具R&R的百分比贡献条形高度与部件间的百分比贡献条形高度之比小于1/99才行。本例中，虽然部件间的百分比贡献条形已经很高大了，但仍然不够。

左中图、左下图显示的是以同一个检验员检验同一个部件为分组变量的Xbar-R“控制图”（严格讲这并不是控制图）。左中图是以每个测量员测量同一个部件的极差形成的R图，数据点绝大多数应该落在控制限之内。本例中虽然所有数据点都落在控制限之内，说明各部件测量结果的极差并无特异者，但此控制限范围太宽，说明重复性误差太大；左下图是以所有部件的总平均值为中心，以重复观测的标准差为标准差绘制的常规控制图，正常情况应该是绝大多数平均值点落在控制域外，因为越多的数据点超出Xbar图的控制限，表明过程实际的波动越大，同时表明测量系统能力越高。左中图、左下图在分析测量系统性能上其实不是十分准确有效的，只能供参考。

右上图是按部件分组的测量结果运行图，一般地，均值连线的变化越大，表明过程实际的波动越大；均值周围的多个散点分布越集中，表明重复性与再现性的波动越小。右下图重叠地显示了三个人员按部件分组的测量结果均值运行图，一般地，连线的变化越大，表明过程实际的波动越大；三条连线越接近平行，表明人员与部件的交互作用越小。这两张图对于改进测量系统的工作是有指导意义的：如果人员与部件有明显的交互作用，则可以通过右下图找出是哪几个部件使得测量员间“分歧”较大（本例中4，5，10号糖果包的测量结果相差悬殊），测量培训中对于这几个部件的深入讨论就可以缩小再现性误差，提高测量的精度。

右中图是按人员分组的测量结果运行图，这条均值的连线的变化越小，表明再现性的波动越小。由于各部件相差悬殊，将每个测量员的全部结果平均之后，一般都看不出显著差异，此图没有什么参考价值。

对于此例，我们可以自己动手直接计算出方差分量，一方面验证上述计算结果，另一方面使我们明白测量数据属于其他结构时的计算步骤。

数据结构是糖果包与测量员二因子间的交叉类型，用第10章学习的计算方差分量方法即可得到相应结果。计算机MINITAB软件对于这种传统数据格式有专门的窗口实现计算：

1．从“统计＞方差分析＞一般线性模型（Stat＞ANOVA＞General Linier Model）”进入。

2．指定“响应（Response）”为“‘测量值’”，“模型（Model）”为“‘糖果包’‘检验员’‘糖果包’× ‘检验员’”，“随机因子（Random Factors）”为“‘糖果包’‘检验员’”。

3．选择“结果（Results）”，勾选“显示期望均方和方差分量（Display Mean Squareand Variance Component）”。

运行命令后可以得到下列结果：

方差分量，使用调整的SS

可以看出，我们自己用直接计算方法所得结果与用上述MINITAB专用模块计算方法完全相同，当然直接计算时还要接着自行求和，并分别求出重复性方差和再现性方差，将二者求和，然后求出总方差，最后计算出两项评价指标。

关于重复性和再现性，这里还有两点需要特别强调。

一是再现性这个概念。重温它的定义，再现性是指在各种可能变化的测量条件下，对同一个测量部件的同一特性进行多次测量，所得结果的一致性。在传统的分析中，常常将再现性的变异来源默认为“测量人员”。现在很多生产环境使用的都是数字式测量仪器，测量人员之间几乎没有差别，我们千万不能认为不需要考虑再现性了，或是生搬硬套地执行重复性与再现性实验。这时候，再现性到底体现在哪里？一定要从实际出发，例如可以从测量仪器、设定初始值、工作班次或其他可能变化的测量条件来考虑可能出现误差的原因，从而设定再现性包括的范围。

二是测量系统变异源分析的问题。在MINITAB的量具R&R研究和例11—2中，只计算和分析了人员和部件两个变异因素，切不可因此认为进行重复性与再现性的分析时所需考虑的变异因素全都如此简单。其实在实际工作中，影响测量系统的因素可能有很多，在没有足够的把握之前，不能轻易地排除其中的任何一个。对此，比较成熟的方法是先进行变异源分析，然后选择最具显著影响的因素进行重复性与再现性分析。关于“变异源分析”的内容，请参阅本书的第10章，在此不再重复。

在测量系统精度分析中，％GageR&R及％P/T两项指标都非常重要，都要满足相应的要求，测量系统的精度才算符合要求。那么两者之间的关系是什么？它们与过程能力指数C_p（其定义及分析见12.6.1节）又是什么关系？

回顾％GageR&R及％P/T两项指标的定义式（11—12）及式（11—13），％GageR&R为：

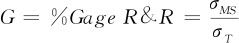
另一个评估指标％P/T为：

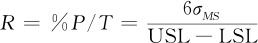
下面就是％GageR&R及％P/T两项指标与过程能力指数C_p的关系式：

事实上，由C_p的定义式（12—6）及式（11—17）的证明中可得

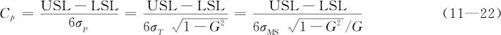
再由式（11—13）可得

将式（11—23）代入式（11—22），则可得式（11—21）：

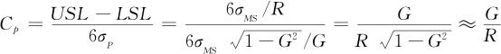
式中的近似号是由于通常G不会太大（例如不超过0.3）而成立的，最大误差率不超过5％。

由式（11—21）容易看出，当测量系统两项精度％GageR&R及％P/T两项指标近似相等时，说明过程能力指数C_p大体上是1；当％GageR&R＞％P/T时，C_p＞1，说明过程能力较好，且％GageR&R及％P/T差别越大，则说明过程能力指数越好；当％ GageR&R ＜％ P/T时，C_p＜1，说明过程能力较差，且％ GageR&R及％P/T差别越大，则说明过程能力指数越差。因此，如果％GageR&R满足要求，而％P/T较大不满足要求（例如％GageR&R＝0.1，％P/T＝0.4），则说明过程能力指数太差了，％GageR&R表面上是合格的，但实际上测量系统的精度还是非常差的，基本上是不符合要求的。反之，如果％P/T满足要求，而％GageR&R较大，不满足要求（例如％GageR&R＝0.4，％P/T＝0.1），则说明测量系统的精度基本上是可用的，只是由于过程能力指数太好，过程的波动太小，必须要求好得多的测量系统才能满足检测过程改进生产水平的状况。总之，％GageR&R及％P/T这两项指标的具体比较非常重要，它反映了测量系统的精度究竟是测量系统精度本身不合乎要求，还是由于过程太好而使测量系统精度未能达到要求，这两种“不合格”的含义是不相同的。

下面介绍另一类测量系统分析方法，主要是先不考虑生产过程的波动，只使用标准件或固定件，这可以对测量系统分析得更细致。

例11—3

某半导体芯片厂对芯片镀膜，公差限是1000±50A，平时生产过程实际标准差σ_P＝15A。我们使用的是光电干涉法测厚仪测量镀膜的厚度，现在要进行测量系统分析。由于是数字显示，测量员差别基本上不用考虑。现在考虑可能造成测量误差的两方面原因：一是不同的测量时刻是否会造成测量误差；二是每次将样件装置于测量底架时的装上卸下的循环是否会造成测量误差。现选用一片固定的芯片，在6时、14时、22时三个不同时刻，各进行装上卸下的3次循环，每次循环中重复测量2次膜厚。试分析本测量系统是否合格（数据列在表11—7中，数据文件：QT_MSA固定件.MTW）。

表11—7　测厚仪测量固定芯片镀膜厚度数据表

解　先画出多变异图获得直观印象。

1．从“统计＞质量工具＞多变异图（Stat＞Quality Tools＞Multi-vari Chart）”进入。

2．指定“响应（Response）”为“‘厚度’”，“因子1（Factor1）”为“‘循环’”，“因子2（Factor 2）”为“‘时间’”。

3．打开“选项（Options）”，勾选“显示单个数据点（Display Individual Data Point）”。

运行后可以得到如图11—11所示图形结果。

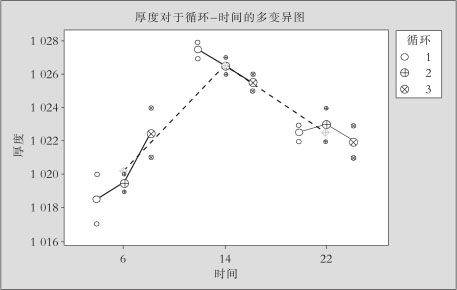
图11—11　测量系统分析固定件多变异图

可以看出，“循环”影响似乎不太大，但“时间”影响显著。

由于两因子“时间”与“循环”是嵌套结构，我们为了计算方差分量可以采用“完全嵌套方差分析”（详见10.5.3节）。

从“统计＞方差分析＞完全嵌套方差分析（Stat＞ANOVA＞Fully Nested ANOVA）”入口：

在打开的界面中，在“响应（Response）”中填写“‘厚度’”，在“因子（Factor）”中填写“‘时间’‘循环’”，则可以得到下列结果，见表11—8。

表11—8　方差分量

这里，同时间、同循环下的波动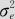就是重复性方差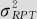，所以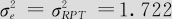是重复性方差；时间的方差及循环的方差两个原因构成了再现性波动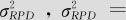9.639＋1.000＝10.639。因此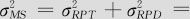，10.639＋1.722＝12.361，故可得到σ_MS＝＝3.516。由于问题描述中已给定σ_P＝15A，所以

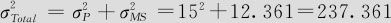
因而σ_Total＝15.4065，由此可以得知％GageR&R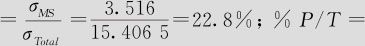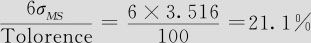。两项指标都没达到合格标准，因为此项指标是过程的关键指标，因而测量系统必须改进。这里“时间”的差异导致测量波动过大的主要部分，必须追究原因。“时间”导致测量结果波动的原因可能有两个：一是虽然测膜厚是在空调室内进行的，但同一天内外界温度变化较大，也可能对测量结果有影响；另一个可能是同一天内不同时刻造成电路上电压不稳定，可能造成误差大。要在深入分析原因后进一步找出解决问题的办法。

本例的因子关系恰好是嵌套结构，因此可以使用MINITAB的“完全嵌套方差分析”窗口，下面介绍应用更为广泛的“一般线性模型”方法。

此问题的模型具体写出来是：

厚度＝时间＋循环（时间）

且二因子皆为随机效应。从“统计＞方差分析＞一般线性模型（Stat＞ANOVA＞General Linear Model）”入口，在“响应（Response）”中填写“‘厚度’”；在“模型（Model）”中填写“‘时间’‘循环（时间）’”；在“随机因子”内填写“‘时间’‘循环’”；选择“结果（Results）”，勾选“显示期望均方和方差分量（Display Mean Square and Variance Component）”，则可以得到最后结果：

方差分量，使用调整的SS

可以看出，本例题用“一般线性模型”计算结果与“完全嵌套方差分析”完全相同。如果实际问题中的模型不是完全嵌套，或者因子更多，或者采集数据不平衡，就可以使用这种应用更广泛的“一般线性模型”计算方法。