4.2　参数的点估计

4.2.1　点估计的概念

假设需要对供应商提供的一批批量为5000个轴承的这个总体的直径进行估计。通常的办法是随机抽取部分比如20个轴承进行测量，而不是测量全部轴承。假设这20个轴承的平均直径是2.12cm，我们就将这批批量为5000个轴承的总体平均直径估计为2.12cm，这种用单个数值对于总体参数给出估计的方法称为点估计。

下面给出点估计的定义：

设θ是总体的一个未知参数，X₁，X₂，…，X_n是从该总体中抽取的样本量为n的一个随机样本，那么用来估计未知参数θ的统计量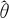（X₁，X₂，…，X_n）称为θ的估计量，或称为θ的点估计。

以后我们总是在参数上方画一个帽子“^”表示该参数的估计量。在工程中经常出现的点估计问题之最好结果是：

对于总体均值μ，；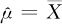

对于总体方差σ²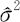，＝S²；

对于比率p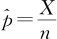，，X是样本量为n的随机样本中我们感兴趣的那类出现的次数；

对于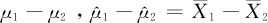（两个独立随机样本均值之差）；

对于p₁－p₂，估计为（两个独立随机样本比率之差）。

常用的点估计值可参见第3章介绍的方法，通过MINITAB软件实现。

4.2.2　点估计的评选标准

点估计量会随着抽取的样本而不同，如果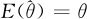，则称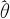是参数θ的无偏估计。由于期望E可以理解为求平均值，因此上式的含义就是，对于θ的估计量具体的一次估计当然可能大些或小些，但取多次的平均值时，应该与原来的参数值相等，不能总是偏大或总是偏小，多次使用时其平均偏差为0。无偏性当然是估计量优良性的一个重要标准，我们应尽量选用无偏估计量或近似无偏估计量。

当有多个无偏估计时，我们希望采用其方差达到最小者。例如在正态总体中，用样本均值来估计总体均值μ，就是所有无偏估计量中方差最小者。

除了上述优良性标准，还有另外一些要考虑的因素。例如对于总体标准差的估计，虽然我们知道样本方差S²是总体方差σ²的最小方差无偏估计，但其平方根则不再是无偏的了。在样本量较小时，其差别非常明显，用S来估计σ总是略偏小一些。为了解决此问题，就要将样本标准差S除以系数c₄，此系数列在本书后附表6中。当样本量n逐渐增大时，此系数将与1非常接近，超过30就可以认为是1了。估计σ的另一类方法是用样本的极差R。如果样本被分成若干组，对于每组都可以先求出组内极差R，对于多组R可以求出其平均值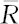，然后将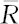除以系数d₂，此系数也列在本书后附表6中。例如，每组只含两个样品时，d₂＝1.128。这样得到的σ的估计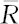/1.128也是无偏的，但这时只考虑了组内的波动。总之，参数估计的方法很多，究竟采用哪一个，要看实际问题的需要，在不同的场合应采用相应的最好的估计量。

采用点估计时，并不能保证在每次估计参数时都是无偏差的，它无法给出对于待估参数的估计的精度和可靠程度的度量，区间估计解决了这一问题。