5.7 样本量的计算
在实际工程应用中,常会出现这样的问题:究竟要采集多大的样本量才能得到我们所需要判断的结论呢?这个问题很复杂,不同的检验问题需要样本量的计算方法是不同的。下面讨论最简单的单样本均值检验问题,原假设是均值为0,备择假设是均值为1的单点情形。检验问题实际上是如何判断一组样本来自哪个总体。假设两个总体的标准差都是σ=1,如果只抽取1个样品,这时它本身就是样本均值,样本均值的分布与原来总体的分布完全一样。我们从图5—27可以看出它们的概率分布图形有很大部分会重叠,当抽取出一个样品后很难判定它是来自哪一个总体。但是,当抽取的样本量超过1个并且将数据取平均值之后,我们知道,这些均值的分布会变得越来越窄,当样本量大到一定程度的时候,比如,取到样本量为25时,从图5—27可以看出,两组样本均值的概率分布图形只有很少部分会重叠,这时就很容易识别两者的差别了。
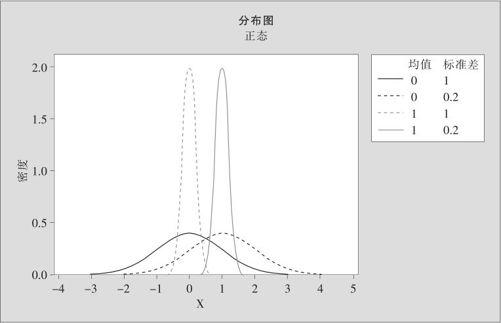
图5—27 不同样本量的样本均值分布对比图
下面的问题是,如果知道两总体确有差别,那么,又该如何确定其样本量保证达到这种分辨开两总体的效果呢?首先引入检验功效的概念。一个检验的检验功效指的是“在原假设不成立的条件下,拒绝原假设的概率”。换言之,由于我们知道,“在原假设不成立的条件下,不拒绝原假设的概率”就是犯第二类错误的概率β,因此“原假设不成立的条件下,拒绝原假设的概率”就应该是1-β。总之,在原假设不成立的条件下,能够拒绝原假设,也就是能够分辨出原假设与备择假设的差别,这就是检验能力的表现,其概率值当然越大越好。我们将侦测到两总体间这种差别的能力称为检验功效,即1-β。
从前几节的内容我们知道,利用抽取的样本情况对总体进行估计或检验时都可能会犯两类错误,样本量的大小取决于决策错误的风险、总体标准差大小、拟检查的差异大小这三方面的因素:通常,如果希望降低犯错误的风险,那么必须增大样本量;随着总体变异性的增大,即总体标准差变大,为了保持原有的风险,样本量必须增大;随着拟检查之差异的变小,样本量必须增大。对于像例5—1那样的右单侧检验问题,其假设是如下简单原假设和简单备择假设的检验问题:
H0:μ=μ0
H1:μ=μ1>μ0
我们记两总体均值的差异为Δ,在本例中,Δ=μ1-μ0,可以结合图5—28看到两类错误的概念,也可以具体得到计算样本量的公式,见表5—17第1行。至于其他类型的检验功效与样本量的计算要更加复杂,此处不再进行公式推导,直接给出了结论。大家只要学会解决下面例5—18类型的问题就很好了。
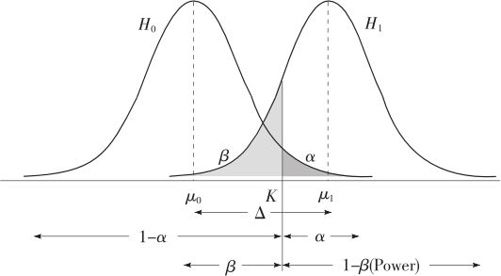
图5—28 两类错误概率及检验功效示意图
表5—17 样本量确定公式一览表
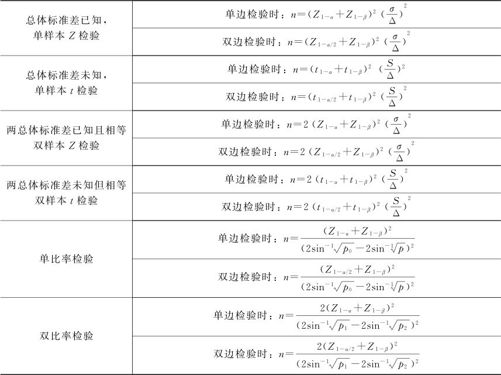
注:由于t分布分位数的数值依赖于自由度,因此使用t检验的样本量计算公式时并不能直接给出结果,实际计算时的最终结果是由迭代法得到的。
例5—18
某钢铁公司项目团队在参数调整后,希望评估冷拉钢筋生产线上的钢筋平均抗拉强度是否能比2000kg有所提高,假定生产线制程的标准差为300kg。经检验,钢筋平均抗拉强度已变为2150kg。问:如果我们选定α=0.05,还要求检验功效达到90%(也就是说,对于平均抗拉强度已提高为2150kg的钢筋样本,被误判为“没有提高”的概率要小于10%),项目团队对于“钢筋生产线上的钢筋平均抗拉强度是否从2000kg有所提高”的检验,需要抽取多少根钢筋才能同时达到这两类风险的要求?
解 根据公式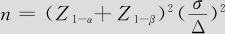 来计算:
来计算:

向上取整为35。即需要抽取35根钢筋才能达到检验功效为90%。在例5—1中,已抽取了25根(这时第一类风险肯定是按原来要求达到5%,但第二类风险则毫无把握),需要再补抽10根,则可以保证第二类风险降到10%。
利用MINITAB计算可以直接得到上述结果:
(1)选择“统计>功效和样本数量>单样本Z(Stat>Powerand Sample Size>1-Sample Z)”;
(2)输入差值“150”,检验功效“0.9”及已知的标准差“300”,保留待计算的“样本数量”为空白,再点击“选项(Options)”后,在“备择(Alternative)”选项中要输入“大于”,如图5—29所示:
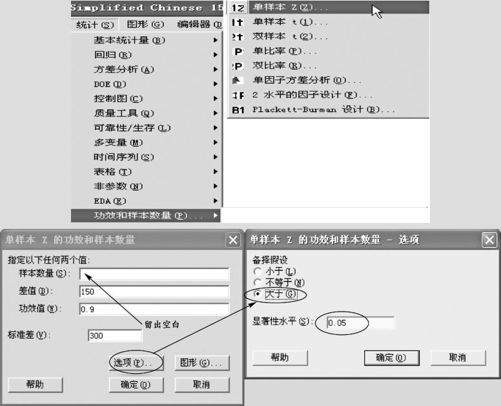
图5—29 求样本量的计算操作图
(3)点击“确定”后,得到以下输出结果及图5—30。
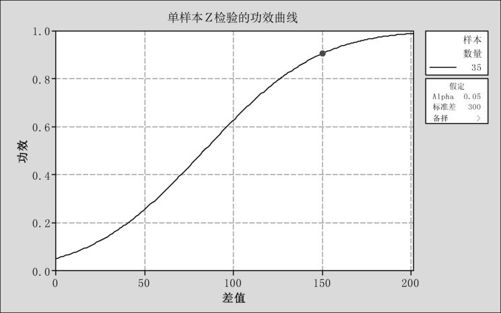
图5—30 检验的功效曲线图
功效和样本数量
单样本Z检验
检验均值=零(与>零)
计算功效的均值=零+差值

(4)输出结果的解释。从计算结果中可以看出,如果要求检验功效为0.9(即第二类错误小于0.1),则样本量至少要35个(其实准确结果是34.3,向上取整才变为35),这时,准确的功效为0.9054,略高于0.9。
如果希望了解例5—1中,抽取不同样本量(如:25,30,35,50,100)时功效状况如何,只要将图5—29的输入方式换成图5—31就行了(输入已知的样本数量,留下待求的“功效值”为空白)。
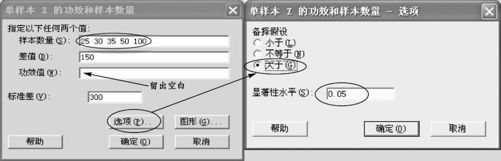
图5—31 求功效的计算操作图
点击“确定”后,得到以下输出结果及图形(见图5—32):
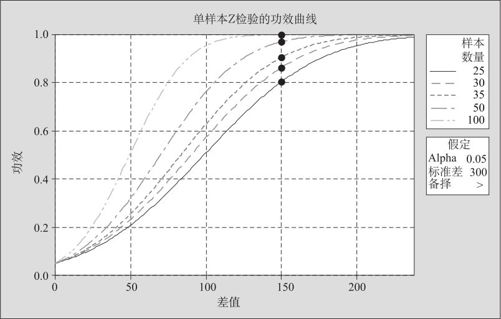
图5—32 检验的功效曲线图
单样本Z检验的功效曲线
功效和样本数量
单样本Z检验
检验均值=零(与>零)
计算功效的均值=零+差值
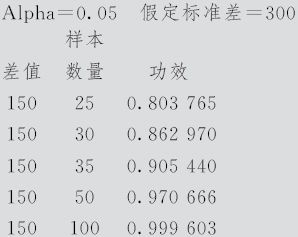
从输出结果可以看出,在例5—1中,抽取25根,犯第二类错误的概率大约为20%,要保证第二类风险为10%,需要补抽10根,即抽取35根方可。
从检验功效曲线图可以看出,在同等条件下侦测相同的差值,样本量越大,其检验功效就越高。
其他类型检验样本量确定的问题,包括检验是单侧或双侧,单样本t检验,双样本t检验,单因子ANOVA等,计算过程大同小异。读者比照例5—18,自己就可以进行计算了,在此不再赘述。
