10.4 变异源分析的数值方法
在本节中,我们将仔细分析各种情况下的数据结构,并给出具体的分析方法。为此,先介绍有关概念,特别是方差分量的概念,然后介绍有关单因子变异源分析的计算公式,并对其含义给予解释。至于10.1节中提出的三个问题,属于两因子或更复杂模型,我们将在10.5节分别加以叙述。
为了理解有关理论,先介绍有关两因子间关系和有关效应的几个概念。
10.4.1 因子间的交叉及嵌套关系
在进行SOV分析时,通常要面对多个因子的状况。由于要同时处理多个因子的效应分析问题,因此首先要搞清楚这些因子间的关系。多个因子间通常都是分层的,在画树状图的时候已经有所体现。而对于相邻层的两个因子,根据它们的不同关系状况,可分为嵌套或交叉关系。在绘制多变异图时,并不需要区分两种关系的不同,但对于变异源的数值分析而言,两种关系就有很大的不同,必须区分清楚。
回顾一下例10—1。在此例中考虑车工车间在生产标准螺钉时的直径波动过大问题。随机选取3名工人,各自分别加工出4颗螺钉,然后在每颗螺钉的根部随机选取两个相互垂直的方向,分别测量其直径,共得到24个数据。将“工人”这个因子记为因子A,将“螺钉”这个因子记为因子B,那么,A与B两个因子间是什么样的关系呢?由于各工人生产的4颗螺钉,是分别附属于相应的工人的,即使我们将这些螺钉都编号为1,2,3,4,但是很明显,工人A和工人B之下的编号皆为1的两颗螺钉并不是同一件东西。这时,称因子B“螺钉”是被因子A“工人”所嵌套着的(Factor B is nested with factor A)。很明显,此种情况下的两个因子所处的地位是不能颠倒过来的。然而,在实际情况中,两个因子间还可能存在另一种关系。例如,3名工人轮流使用共同的4台编了号的车床,每个工人都使用了车床1,2,3,4,这时,工人A和工人B之下的编号都为1的两台车床是同一件东西。而且可以反过来说,每台车床都被3名工人使用过。这时,称因子B“车床”是与因子A“工人”相交叉(Factor B is crossed with factor A)。很明显,如果这时候说因子A“工人”与因子B“车床”相交叉也是同样的,它们的位置是可以颠倒过来的。这里要注意,单从树状图上是不能区分两个因子的关系是交叉还是嵌套的,只能从实际意义判断之。
在例10—2中轴杆长度问题中,选取3个工人,让他们轮流使用固定的编好号的4台车床,按随机顺序各自分别加工出3根轴杆。若将与因子A(工人)及搭配的因子B(车床)的每台车床编好号,则可以发现,因子A(工人)与因子B(车床)间的关系是交叉关系。注意,它们两因子间可以颠倒顺序,即可以反过来说,因子B(车床)的每个值也都与因子A(工人)的每个值搭配过。如果车床不是固定的编号的车床,而是每个工人各自有自己固有的4台车床,这时因子A(工人)与因子B(车床)间的关系就不再是交叉关系,而是嵌套关系了。
例10—3讨论的是三因子问题。由于不能将轴棒之间的变异看成随机误差,因而要求将轴棒之间的变异也看作因子,即形成三因子问题。这里3个工人(因子A),分别使用已选好并编了号的4台车床(因子B),各自分别加工出3根轴棒(因子C),然后对每根轴棒测两次直径(误差)。由于因子B的4台车床是固定的,所以工人(因子A)与车床(因子B)之间是交叉关系,而轴棒(因子C)则是被A与B所嵌套的,即三因子是先交叉后嵌套的关系。
如果将例10—3的安排稍加调整:3个工人(因子A),分别使用自己固定的4台车床(因子B),各自分别加工出3根轴棒(因子C),这时因子间的关系就会发生变化。这时B被A所嵌套,C被A,B所嵌套,这种关系也称为完全嵌套关系(fully nested)。
实际问题中可能有多种结构,但仔细分析它们的数据就可以发现,因子间的关系无非是嵌套或交叉这两种基本类型。有时在实际问题中可能遇到的是因子个数较多,关系较复杂,这时需要仔细分析处理之。
10.4.2 固定效应与随机效应
下面讨论每个因子本身的效应问题。一个因子可以取若干个不同的数值,这些数值称为该因子的水平(level)。对于此因子所取的每个水平下响应变量取值的均值的算术平均值,称为此因子的因子总均值。如果对于此因子所取的各个水平,响应变量取值的各水平均值与此因子的总均值有差别,则称这个差别(因子所取的各个水平下响应变量取值的均值减去此因子的总均值)为此因子在该水平上的效应(effect),即因子取此水平时会使响应变量取值的均值在本因子的总均值上产生多大改变。
这种效应有两种不同的情形:固定效应和随机效应。如果对于每个特定的水平,其效应是一个固定的数,称此种效应为固定效应(fixed effect),此因子称为固定效应因子(factor with fixed effect)。比如在比较多个总体均值是否相等时使用的方差分析方法,所遇到的都是设各因子的效应是固定效应的例子。但实际生活中还有另一种类型,各因子在各水平上的效应不再是固定的数值,而是一个随机变量。此种效应称为随机效应(random effect),此因子称为随机效应因子(factor with random effect)。本章中所讨论的变异源问题一般都将各因子考虑为随机效应因子。比如例10—1,因子A(工人)有A,B,C共3个水平,这3个水平是从这个因子A(工人)所有可能取值的集合中随机抽取的,它们的效应不再是固定的数值,而是个随机变量。这时,我们所感兴趣的焦点,不是具体分析出各自的效应是多少,而是希望得知这种效应的变化有多大,此种效应属于随机效应,因而因子A(工人)是随机效应因子。我们对此的处理方法是,将此因子所有各个水平(总计为nA个)的效应值看成是个总体,而因子第i个水平的效应αi是来自此总体的一次抽样(i=1,2,…,nA)。显然此总体的均值应为0,而我们感兴趣且又非常重要的常量是该因子的方差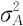 ,此常数与i无关,而仅与因子A有关,称为因子A的方差分量(variance component)。因此,有
,此常数与i无关,而仅与因子A有关,称为因子A的方差分量(variance component)。因此,有

式中,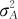 未知。在SOV中,最重要的任务就是估计这个参数
未知。在SOV中,最重要的任务就是估计这个参数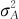 。
。
对于其他各因子我们也采用同样的处理方法。而SOV的最终目的是将各个因子的方差分量按照由大到小的顺序排列出来,这就是它们对总变差的贡献。将它们换算为百分数,就是各个因子对于总变差的贡献率,而按贡献率由大到小的排序就是进行“变异源分析”的最主要目标。
分析随机效应因子与固定效应因子是很不同的。由于以前介绍过的ANOVA中处理的都是固定效应因子,因此我们必须在ANOVA的基础上,经过进一步计算才能得到方差分量的值。显然,求方差分量的工作要远比ANOVA难得多。
另外一点值得注意的是,因子之间的关系是嵌套或是交叉,与这些因子本身有固定效应还是随机效应是没有关系的。换言之,两个皆为固定效应因子(或皆为随机效应因子)之间,或一个随机效应因子与一个固定效应因子之间,既可以是嵌套关系,也可以是交叉关系。
当然,这里也要注意到另一件事:两个是交叉关系的随机效应因子,除了考虑它们每个因子的主效应方差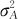 及
及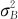 外,还应该考虑到它们之间可能存在的交互效应方差
外,还应该考虑到它们之间可能存在的交互效应方差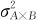 。而对于两个是嵌套关系的随机效应因子,它们之间则不可能存在交互效应方差项。这是因为,如果因子B被因子A所嵌套,因子B不可能取固定的各个水平,因子B所取的各个水平将依因子A的不同水平而不同,这时,它们之间是没有交互作用可言的。我们将只考虑因子A的效应方差
。而对于两个是嵌套关系的随机效应因子,它们之间则不可能存在交互效应方差项。这是因为,如果因子B被因子A所嵌套,因子B不可能取固定的各个水平,因子B所取的各个水平将依因子A的不同水平而不同,这时,它们之间是没有交互作用可言的。我们将只考虑因子A的效应方差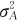 和因子B被A所决定的各个水平效应的方差
和因子B被A所决定的各个水平效应的方差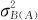 。根据固定效应与随机效应的定义,可以得知,在两因子为交叉关系时,只有两者皆为固定效应时,其交互作用才是固定效应的;只要有一个因子是随机效应的,则交互效应肯定是随机效应的,都要考虑计算方差分量。至于有交叉关系的两个因子间,是否一定存在交互作用呢?两因子间确实可能并没有交互作用存在。对于这种情况,通常是先假设它们存在交互作用,然后通过假设检验的方法,给出它们之间是否有交互作用的判断。如果它们的交互效应真的不显著,则可以把它们的交互效应再从模型中剔除出去。
。根据固定效应与随机效应的定义,可以得知,在两因子为交叉关系时,只有两者皆为固定效应时,其交互作用才是固定效应的;只要有一个因子是随机效应的,则交互效应肯定是随机效应的,都要考虑计算方差分量。至于有交叉关系的两个因子间,是否一定存在交互作用呢?两因子间确实可能并没有交互作用存在。对于这种情况,通常是先假设它们存在交互作用,然后通过假设检验的方法,给出它们之间是否有交互作用的判断。如果它们的交互效应真的不显著,则可以把它们的交互效应再从模型中剔除出去。
10.4.3 单因子方差分量计算公式
在因子个数不同或因子间关系不同(嵌套还是交叉)时,方差分量的计算公式是很不相同的。本段将只介绍最简单的单因子方差分量的计算。
设Yij为因子A在其第i个水平时所得到的第j个观测值,则可以假定下列模型:
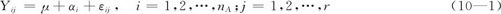
式中,μ为总平均值,是非随机参数;αi是总体Ai的随机效应,是随机变量;εij是随机误差。对于各随机项有下列假定:
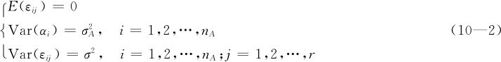
这里εij与αi皆不相关。
模型(10—1)与模型(10—2)就是所要讨论的单因子方差分量模型。在此模型中,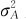 及σ2称为方差分量。对这个模型研究的重点放在方差分量的估计上,对于这两个参数的假设检验(这时还要增加它们都是正态分布的假定)就不进行讨论了。
及σ2称为方差分量。对这个模型研究的重点放在方差分量的估计上,对于这两个参数的假设检验(这时还要增加它们都是正态分布的假定)就不进行讨论了。
我们注意到,这种问题的分析方法与普通的方差分析法是非常不同的。在得到方差分析的表格ANOVA后,已经可以算出各分量的离差平方和SS,相应的自由度df,从而可以得到各分量的平均平方和(简称为均方)MS,包括MSA和MSE。但这里计算的SS只是根据观测到的数据直接计算其离差平方和得来的,这对于固定效应的模型足够了。然而,如果A因子是随机效应因子,各水平下观测值的离差平方和既包含A因子方差的影响,还包含随机误差的影响,为了求出单纯的A因子的方差必须在扣除随机误差的波动影响之后才有可能。因此,求方差分量的估计还要以ANOVA计算出的MS为基础,再进行下一步计算才行。可以证明有下列公式(参见参考文献[15]蒙哥马利:《实验设计与分析》,92页):

其中各项MS是ANOVA表中的均方,我们在式(10—3)中给出的是它们的期望值,对这些期望值用对应的均方的观测值来估计,可得到下列方程组:

解此方程组,就可以得到方差分量的估计:

10.4.4 单因子方差分量计算举例
为了演示上面各项计算的含义,举一个单因子方差分量例子。
例10—4
某瓷砖厂每天烧制一炉瓷砖,每炉随机抽取5块,分别测量其平面度(flatness)。连续抽取了7天,共记录了35个数据,如表10—4所示(数据文件:QT_SOV1瓷砖.MTW)。试分析其平面度变异的成因。
表10—4 瓷砖平面度数据表

经由MINITAB软件,绘制出多变异图(绘制方法见10.3节,操作参见图10—2及图10—3),结果如图10—5所示。从图10—5中可以看到,尽管每天的5块瓷砖平面度间有差异,但很明显的是7天之间瓷砖平面度间的差异似乎要大得多。
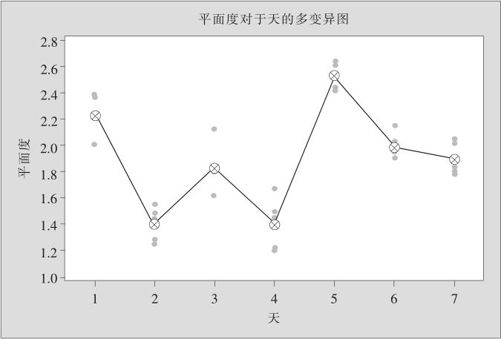
图10—5 瓷砖平面度数据的多变异图
为了获得更准确的两个方差分量的数值结果,我们使用MINITAB具体计算两个方差分量。其操作步骤如图10—6所示。
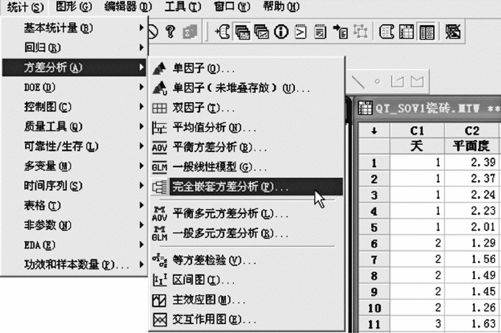
图10—6 完全嵌套方差分量计算操作(1)
从“统计>方差分析>完全嵌套方差分析(Stat>ANOVA>Fully Nested ANOVA)”入口(见图10—6)。
在如图10—7所示界面中,在“响应(Response)”中填写“‘平面度’”,在“因子(Factor)”中填写“‘天’”,则可以得到结果。
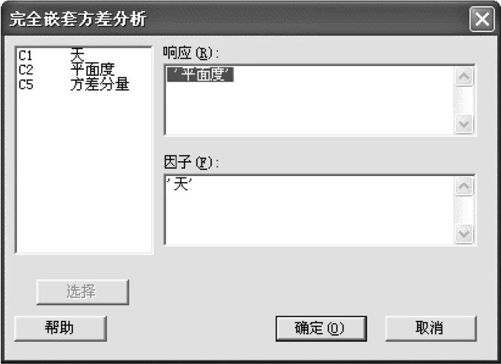
图10—7 完全嵌套方差分量计算操作(2)
注意:本操作窗口能计算的是所有因子是完全嵌套时的随机效应模型,由于本例只有一个因子,当然也可以借用此窗口功能,以后我们还会使用此窗口来计算更复杂的例子。在打开的窗口中填写相应信息即可(见图10—7)。
计算结果如下所示:
嵌套ANOVA:平面度与天
对于平面度的方差分析

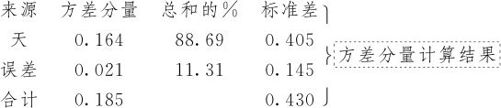
方差分量
期望均方
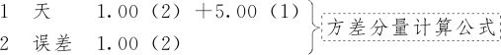
我们要对此表进行仔细分析,搞懂每个输出的结果。
首先看方差分析表,本例中只有一个因子A“天”,其余完全是随机误差。将因子A及误差两项的离差平方和除以相应自由度,可以得到相应于A的均方MSA=0.8403及误差均方MSE=0.0209。但是要注意这里的因子A的均方是将A因子各水平当作固定效应来计算的,而实际上,A是随机效应因子,它的几个水平间(也就是几天平均值间)的差异,并不是固定数值间的差异(那时就根本不存在“方差”的概念),它们的波动之成因除了A因子自身的方差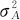 之外,还有随机误差的σ2在起作用,因此不能把MSA完全归因于A因子自身的变异原因
之外,还有随机误差的σ2在起作用,因此不能把MSA完全归因于A因子自身的变异原因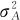 。在MINITAB输出结果中的最后一段“方差分量计算公式”内,还附带给出了具体计算公式:
。在MINITAB输出结果中的最后一段“方差分量计算公式”内,还附带给出了具体计算公式:
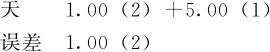
这是代入式(10—4)的具体结果,写成真正的公式是:

在方差分量计算公式中,用“(1)”代表最高层的方差(本处是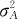 ),用“(2)”代表最基层的随机误差(本处是σ2),方差分量计算公式主要是给出了相应系数。如果把具体数值代入式(10—6)就可以得到下列方程:
),用“(2)”代表最基层的随机误差(本处是σ2),方差分量计算公式主要是给出了相应系数。如果把具体数值代入式(10—6)就可以得到下列方程:
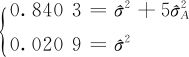
由此容易解出(直接代入式(10—5)也一样):
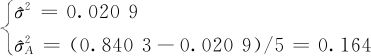
这就是方差分量计算的最终结果。
在方差分量结果段中,还给出了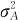 和σ2各自所占的百分比,
和σ2各自所占的百分比,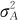 占总和高达88.69%,而σ2只占总和的11.31%。这就从数值上定量地给出了各项方差在总方差中所占的比率。
占总和高达88.69%,而σ2只占总和的11.31%。这就从数值上定量地给出了各项方差在总方差中所占的比率。
将方差分量结果中的前2列粘贴入原数据工作表QT_SOV1瓷砖.MTW中第4,5列(见图10—8),然后绘制Pareto图。从“统计>质量工具>Pareto图(Stat>Quality Tools>Pareto Chart)”入口(见图10—8中下图),在“缺陷或属性数据在”中填写“‘来源’”,在“频率位于”中填写“‘方差分量’”。
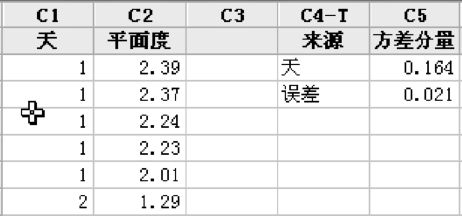
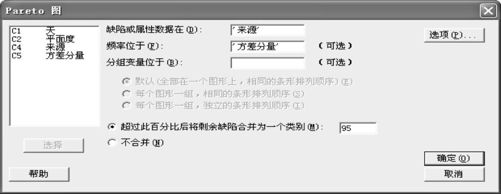
图10—8 由方差分量画Pareto图的操作
经MINITAB处理后可以得到Pareto图如图10—9所示。

图10—9 瓷砖平面度变异源的Pareto图
从此图中可以看出,天与天之间的差异确实是非常显著的,它对于总变异的贡献率高达88.6%。
这里要注意,上述计算方差分量的方法有时可能得到负的方差分量估计。此时通常可以认定该方差分量为0就行了。另外,如果需要考察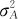 到底有多大,可以考虑用更精确的公式求出比值
到底有多大,可以考虑用更精确的公式求出比值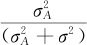 的置信区间,详细内容请参见参考文献[15](蒙哥马利:《实验设计与分析》,97页)。
的置信区间,详细内容请参见参考文献[15](蒙哥马利:《实验设计与分析》,97页)。
