2.5　中心极限定理

为了给今后研究统计学问题打下好的基础，我们要在概率基础的最后一节介绍中心极限定理。从严格的数学意义上来讲，中心极限定理内容非常丰富，但我们只介绍今后研究统计问题时会遇到的最重要的两个结论。而且准确地说，第一个结论算不上是中心极限定理的内容，这里只不过按照一般六西格玛教材中的普遍说法加以陈述罢了。

2.5.1　样本平均值的标准差性质

我们通常会讲到随机变量的独立性。我们说“两个随机变量X₁与X₂是相互独立的”，指的就是：其中一个随机变量的取值不会影响另一个变量的取值。对于多个随机变量也是一样的意思。我们研究统计学的时候，各样本间就是相互独立取值的有相同分布的随机变量。对于这种类型的问题，在本章的2.2.2节中曾讨论过。在讲述方差的性质时，讲到了下述性质（见式（2—10）及式（2—11））：

如果有多个随机变量，它们相互独立，而且方差都相等（记为σ²），则

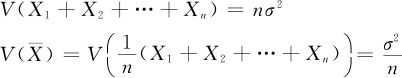
这个性质就是说，的方差与原来X的方差相比，的方差是原来X的方差的n分之一。将此式更明确地写出，就是

或者写成标准差的形式：

要注意的是，式（2—68）和式（2—69）的成立并未要求原来分布为正态，这两个公式对于任何分布都是正确的。

2.5.2　样本平均值的分布性质

大家容易理解，两个随机变量的分布类型不同，那么各自抽取10个样本（也就是10个独立同分布的随机变量），两个随机变量各自形成的分布当然也会不同。但是，大量实践表明，它们都与正态分布接近。概率论的理论证明了这样一个重要定理，我们称之为中心极限定理，通俗的描述就是：

随着样本量的无限增长，无论原来的分布是什么（离散分布或连续分布，正态分布或非正态分布），的分布总会趋向于正态分布。

实际工作中，只要n较大时，我们就可以认为，的分布近似于正态分布。当分布对称时，n＝5已经近似得很好；当分布严重偏斜时，n＝30也会近似得很好。

此定理的严格证明不再给出，但我们给出几个例子加深理解其含义。

我们选“凹三角”分布和“均匀分布”作为对称分布的代表。n＝1代表原分布；n＝2代表两个同样随机变量的平均值的分布；n＝5代表5个同样随机变量的平均值的分布。从图2—58中上两排图可以看出，对于对称分布，5个样本的平均值的分布已经与正态分布很接近了。我们选指数分布作为严重偏斜分布的代表，5个样本的平均值的分布形状离正态分布还很远，但是30个样本的平均值的分布则与正态分布很接近了。我们在数据文件BS_中心极限定理.MTW中，给出了示意性的数据供大家参考。如果需要正式进行正态性检验，则要在学习第5章之后才能实行。

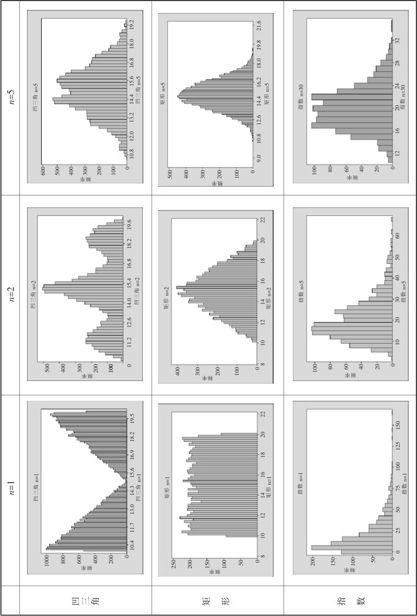
图2—58　中心极限定理示意图