12.1　控制图基础理论

导致质量产生变异的因素很多，根据因素对产品质量影响的大小和性质，可以将其分为两大类：一类是特殊因素；另一类是随机因素。特殊因素很多，如工艺过程的变动、刀具的过度磨损、人员的变动更换等。这些因素对产品质量的影响是显著的，在技术上容易识别并消除。随机因素也有很多，如温湿度的轻微变化、仪器的微小振动、原材料的细微差异等。这些因素对产品质量的影响是细小的，在技术上不易识别，更不可能消除，但如果从根本上改变了过程，则这种波动会大幅减少。休哈特认为，可以以μ±3σ为控制限建立控制图把特殊因素和随机因素区分开来。

控制图是对过程质量特性值进行测定、记录、评估和监测，以判断过程是否处于统计控制状态的一种用统计方法设计的图形。通常控制图的横轴总是时间，而其纵轴则可以有多种选择，例如可以是单值，也可以是小组均值，可以是小组极差，也可以是小组标准差，等等。一般说来，可以用统计量T来代表。对于T的分布，我们认为它们是正态分布或近似为正态分布。实际上，控制图是统计量T的正态分布图在时域上的具体展示，它由T的中心线μ、上下控制限μ±3σ和按时间顺序抽取样本并用其统计量的数据点T这三个基本要素组成。对于服从或近似服从正态分布的统计量T，大约有99.73％的数据点会落在上下控制限之内，数据点落在上下控制限之外的概率约为0.27％。根据假设检验的小概率原则，一旦有界限之外的数据点出现，就可判为异常点，即认为它们是由特殊因素造成的过程变异。SPC控制图的基本原理可用图12—1概括表示。

图12—1　SPC原理示意图

包括“点出界就判异”的准则在内，SPC中共有8条判异准则用来判断过程是否受控。为了便于具体地说明这8条准则，可将控制图分为6个区，每个区的宽度为σ。6个区的标号为A，B，C，C，B，A，两个A区、B区、C区都关于中心线对称（见图12—2）。

图12—2　控制图的分区

根据控制图的分区定义，8条准则可以表达为：

（1）1点落在控制限之外。

（2）连续9点落在中心线同一侧。

（3）连续6点递增或递减。

（4）连续14点中相邻点升降交错。

（5）连续3点中有2点落在中心线同一侧的B区之外。

（6）连续5点中有4点落在中心线同一侧的C区之外。

（7）连续15点落在C区之内。

（8）连续8点落在中心线两侧，但无1点在C区之内。

统计学上可以证明，以上8种现象出现的概率大体都等于或接近于0.27％，小概率事件的发生导致我们判定过程为异常。

这里要注意，在8条判异准则中，前4项其实与分区无关，而后4项判断法则都是在正态条件下，将±3σ区域分成6个子区，按照正态分布在各区中应该出现的概率来制定的法则，因此，后4条只有当监控统计量严格服从正态分布时才有意义，故后4项判断法则只对单值X及小组均值的控制图使用，其他各控制图皆只使用前4项法则。

控制图的类型很多，常用的控制图按数据类型分为两类：对于连续变量用计量控制图；对于离散变量用计数控制图。前者有单值—移动极差图（I-MR Chart）、均值—极差图（Xbar-R Chart）、均值—标准差图（Xbar-S Chart）；后者有不合格品率图（P Chart）、不合格品数图（NP Chart）、单位产品缺陷数图（U Chart）和缺陷数图（C Chart）。

综合考虑数据特点和抽样方法等因素，可以归纳出如图12—3所示的“常用控制图的选择路径图”。

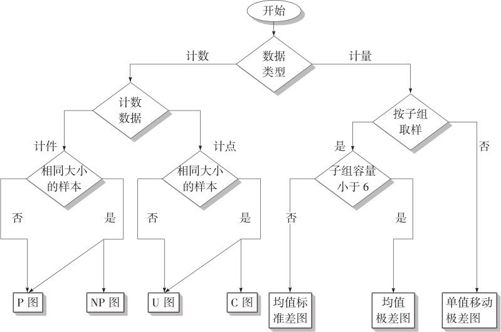
图12—3　常用控制图的选择路径图

根据应用目的不同，控制图又可分为分析用控制图与控制用控制图两个阶段。一个过程开始实施控制图时，通常不会恰巧处于统计控制状态，总会存在些异常波动。如果就以这种状态下的参数来建立控制图，上、下控制限的间隔一定较宽，这会导致判断失误。因此，开始过程控制时，总需要将失控状态调整到统计控制状态，这就是分析用控制图的阶段。

国标中规定，制定分析用控制图时，在合理分组的前提下，至少要采集25组数据，用来计算控制限。如有越界者要根据实际情况判定是否确实出现异常原因，确有异常原因（简称异因）者可以删除此组数据，未发现异因者必须保留此组数据且增大观测组数。分析用控制图阶段要解决的第一个问题是：调整过程，消除异因，以使过程受控；分析用控制图阶段要解决的第二个问题是：在过程受控后，再改进过程，以确保过程能力指数C_p或C_pk等能达到顾客要求。一旦过程实现了上述两点，就可延长控制限作为控制用的控制图，进入控制用控制图阶段，在线使用。在此阶段，一旦判异，应停产检查找出异因，并在消除异因后再恢复生产，以保持过程的统计控制状态。