13.4　部分因子试验

因子试验中最有魅力的内容不是全因子试验，而是大大减少了试验次数的部分因子试验。如果在减少试验次数的条件下仍然能够获得足够的信息，这当然是工程师们求之不得的好方法。

13.4.1　部分因子试验概论

13.4.1.1　部分因子试验的必要性

大家都知道，进行2水平全因子试验设计时，全因子试验的总试验次数将随因子个数的增加而急剧增加。例如，4个因子需要16次试验，6个因子就需要64次试验。但仔细分析所获得的结果可以看出，建立的6因子回归方程包括哪些项呢？除常数项外，估计出来的主效应项有6项，2阶交互项15项，3阶交互项20项，…，6阶交互项1项，详细结果列成表13—15。

表13—15　全因子试验系数分布表（6因子）

容易看出，回归方程中除了常数项、一阶主效应项及二阶交互效应项外，共有42项是3阶及3阶以上的交互作用项，而这些项实际上已无具体的物理意义了。这自然会提出一个问题：能不能少做些试验，但又照样能估计方程中的常数、1阶及2阶项系数呢？如果能够这样，那就有很重要的应用价值了。部分因子试验就是使用这种方法，它可以用在因子个数较多（例如5个以上），但只需要分析各因子和2阶交互效应是否显著，而并不需要考虑高阶交互效应时，这将使试验次数大大减少。

13.4.1.2　部分因子试验的实施原理

下面，用简单例子说明部分因子试验的实施原理。

例13—10

有A，B，C，D共4个可控的试验因子，每个因子都为2水平。如何只进行8次试验，而且使分析效果达到最好？

解　方案1：删节试验方法。我们设想，4个试验因子，每个因子都为2水平，做全因子试验要16次。我们从这16次试验中，选出8次来做，希望照样能分析主效应，是否可行？如何选？

先列出全因子设计的16次试验计划表（如表13—16所示）：

表13—16　4因子全因子试验计划表

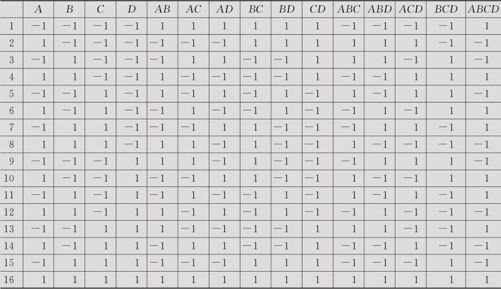
按照表13—16的前4列安排试验，对于最终获得的数据结果可以分析出所有主效应，2阶交互效应，也可以分析出3阶、4阶交互效应。先想：从16次试验中随机挑8次，行吗？显然不行。因为很可能挑成这样：某些因子在8次试验中，取高水平及低水平次数并不恰好相等。这时，原来正交试验的“均衡分散，整齐可比”的优点不复存在，分析方法要另搞一套才行，这当然是我们不希望看到的。我们知道，在上述正交表中，任何一列都与另外一列“正交”，因此，固定将某列（比如最后一列“ABCD”）取“1”的8行予以保留，而删去取“－1”的8行，这样可以保证在保留的8行表中，A，B，C，D这4列中皆有4行取“1”，4行取“－1”，且各列间仍然保持“均衡分散，整齐可比”，即可以保持正交性。设定取ABCD＝1，结果见表13—17。

表13—17　减半实施的4因子全因子试验计划表（ABCD＝1）

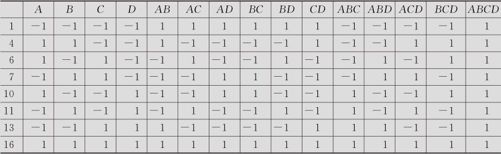
仔细分析可以发现，原来16行的正交表13—16中，15列是完全不同的。但删去8行后（见表13—17），除去一列全为1外，另14列中，每列都有与之成对的另一列是完全相同的。例如，ABCD＝1的表中，D与ABC完全相同，记为D＝ABC。完全相同的两列，在作分析时，计算出的效应或回归系数结果完全相同。这两列的效应就被称作“混杂”（confounded）了。也可以换个说法：这时，D与ABC互为别名（D is the alias of ABC）。

是否可以选别的条件作为删去8行的标准呢？例如，选BCD＝1，也是可以的。这时，由于D＝BC，显然不如D＝ABC好。经比较后，可知ABCD＝1这种安排方法是所有安排中效果最好的。

混杂总是坏事，能否不产生混杂呢？答案是：任何部分因子试验，混杂是不可避免的。我们只是希望混杂安排得更好些，尽量让我们感兴趣的因子或交互作用只与更高阶的交互作用相混杂，而在通常情况下，3阶或更高阶的交互作用项是可以忽略不计的，这时，我们感兴趣的因子或交互作用就都是可以估计的了。

方案2：增补因子方法。我们设想，总计8次试验，由于每个因子都为2水平，做全因子试验可以安排3个因子，假设A，B，C这3个因子已安排在前3列了，现在有4个因子要安排，如何安排这新的第4个因子呢？如何办才好？此问题的描述见表13—18。

表13—18　3因子全因子试验计划表

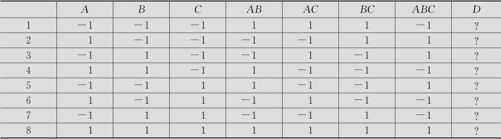
原来的这个表有8行7列，任意两列间是相互正交的。我们希望增加一列来安排因子D，而且希望此列仍然能与前面各列保持正交性。能否找出一个与前7列不同的列，且与前面各列保持正交呢？数学上可以证明，这是不可能的。换言之，D这列必然要与前面第4，5，6，7列中某列完全相同。权衡之下，我们认为，取D＝ABC是最好的安排。将D取值设定与ABC列相同，并将其前移至第4列，可以得到表13—19。

表13—19　减半实施的4因子试验计划表

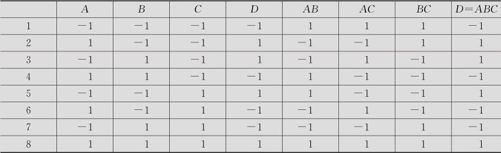
而将ABCD＝1的表13—17重新排序后，将与表13—19完全相同。

很明显，ABCD＝1这个约定非常重要。这将导致A＝BCD，B＝ACD，C＝ABD，AB＝CD，AC＝BD及AD＝BC，即某些主效应将与3阶交互效应相混杂，某些2阶交互效应将与另一些2阶交互效应相混杂。从上述结果很容易发现混杂的规律。我们可以用下列法则来表述：对ABCD＝1这个等式两边都乘以A，由于AA＝1，因此就能得到：BCD＝A。同样，也可以得到D＝ABC及AB＝CD等。这种运算规则简单易用，相当于任何字母在等式两侧可以随意移动，只要不“无中生有”就行。这个法则对2水平的部分因子试验设计总是成立的。

如果约定改为ABC＝1，这将导致，A＝BC，B＝AC，C＝AB，某些主效应将与某些2阶交互效应相混杂，这个设计ABC＝1将比设计ABCD＝1的混杂情况要差很多。在部分因子试验中，要想使混杂情况尽可能地好且照顾到自己的问题的实际需求，则要用到较多的试验设计知识和技巧。20世纪60年代，日本的田口玄一博士提出用“点线图”的方法来计算交互作用法则，现在看来这种方法既烦琐又不够准确；中国的统计学家从70年代起就提出了一整套“表头设计”法则，这套方法很有效，但需要有相当多的实践经验后才能熟练掌握。目前国内很多书籍仍然倡导工程师们用查“交互作用列表”的方法掌握表头设计，而且倡导大家仍然用手算的方法进行试验结果的分析。笔者认为，能够学会表头设计并会自己手算对结果的分析当然很好，但毕竟要花费太多的精力。计算机软件已经提供了更简单的设计及计算功能，不但不需要再学“点线图”，而且可以不再去进行大量的“表头设计”的练习。对于部分因子试验设计的一般需求，计算机已经可以自动提供最佳的设计供人们使用；如果有更高或更灵活的要求，也只要学会下文介绍的简单易懂的“别名运算法则”，再加上计算机的辅助输出，就足以应付一切了。因此，一般使用试验设计的工程师们不必再花力气去掌握“点线图”和“表头设计”这些烦琐的内容。但这里要提醒大家的是：下面介绍的有关概念确实很重要，即使直接使用计算机也要理解好这些概念才行。

13.4.1.3　部分因子试验的关键概念——分辨度

下面通过例13—11介绍部分因子试验的几个关键概念。

在例13—10中，为了在8次试验中安排A，B，C，D共4个因子，在表13—18的3因子8次试验安排中，让D因子与ABC交互作用相混杂，则称D＝ABC为“生成元”（generator）。经过仔细分析后发现，这样的安排其实等价于表13—16内16次试验中保留ABCD＝1的那些试验。称ABCD＝1（或写为I＝ABCD）为“定义关系”（defining relation），简称“字”（word）。在新因子只有一个时，“生成元”与“定义关系”是同一件事的两种表达方式，但用“生成元”来考虑问题会简单些，因为此时是在较少的试验次数下安排更多因子的问题。当新因子个数增多时，“生成元”当然会增加，但“定义关系”的总个数会增加得更多。例13—11将介绍更多“生成元”的情况，并给出“生成元”与“定义关系”间的关系。

例13—11

有A，B，C，D，E，F共6个可控的试验因子，每个因子都为2水平。如何能在16次试验中安排而获得最好的混杂结果？

解　考虑16次试验可以安排4个因子的全因子试验，这4个因子A，B，C，D称为“基本因子”。问题是如何安排另两个因子E和F。比较下列两个方案。

方案1：令“生成元”为：E＝BCD，F＝ABCD。这时立即可以看到的是定义关系I＝BCDE和I＝ABCDF，但注意这两个定义关系的乘积一定也是定义关系，所以有I＝（BCDE）（ABCDF）＝AEF。通常将其写成一整串的形状：I＝BCDE＝ABCDF＝AEF。考虑其混杂情况，我们发现I＝AEF意味着A＝EF，E＝AF和F＝AE，即有些主效应与2阶交互效应相混杂了。

方案2：令“生成元”为：E＝ABC，F＝ABD。这时立即可以看到的是定义关系I＝ABCE和I＝ABDF，且有I＝CDEF，即I＝ABCE＝ABDF＝CDEF。考虑其混杂情况，我们发现这时没有任何主效应与2阶交互作用相混杂的情况，只有某些2阶与2阶交互效应相混杂，例如AB＝CE等。

从上面两个方案的比较容易看出，方案2优于方案1。我们要考虑到底应该用什么指标来作为部分因子试验优劣的评审标准。显然，造成方案1不好的关键是因为有个定义关系I＝AEF所含字母只有3个，它的“长度”太短了。为此，我们引入部分因子试验的最关键指标——分辨度。

我们称所有的字中字长最短的那个字的长度为整个设计的分辨度（resolution）。分辨度通常用罗马数字给出（前6个数字是Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ，Ⅵ）。从分辨度定义可以看出，如果一个因子设计中，因子的个数及试验次数给定时，能使分辨度达到最大的当然是最好的设计。

我们进行更一般的讨论，如果一共考虑k个因子，p代表新安排的因子个数（当然这意味着有k－p个因子是设计表中原有的“老因子”或基本因子），这样的试验记作2^k－p（比如例13—11的设计就应记为26^－2）。对这个记号可以有两种解释方法：一方面，将k－p当作一个数来看待，此数恰好是安排进行全因子试验的“老因子”或基本因子的个数，2^k－p作为一个数字来看，它正好是试验进行的次数；另一方面，当然也可以这样解释，比如例13—11的试验2^6－2，可以将其写成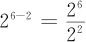，分子为因子个数是6时的全因子试验次数64，分母是2的2次方，表示只实行了1/4，或减半了两次。这两种理解都有意义。因此，2^k－p是部分因子试验设计的很恰当的记号。

设计2^k－p一共有p个生成元（比如例13—11就有2个生成元），一共有2^p－1个定义关系（比如例13—11就有3个定义关系）。在方案1中，3个定义关系中字长最短为3，所以方案1的分辨度为Ⅲ。在方案2中，3个定义关系中字长全是4，所以方案2的分辨度为Ⅳ。又比如例13—10，设计2^4－1的生成元是D＝ABC，定义关系为I＝ABCD，则这是分辨度为Ⅳ的设计。

如果将分辨度标注在因子设计记号的右下角，则我们把例13—10的设计记为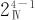；例13—11的设计方案2记为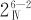。一般地，分辨度为R的部分因子设计记为。

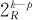我们有必要再详细解释一下分辨度的含义。

分辨度为Ⅲ的设计：各主效应间没有混杂，但某些主效应可能与某些2阶交互效应相混杂。

分辨度为Ⅳ的设计：各主效应间没有混杂，主效应与2阶交互效应间也没有混杂，但主效应可能与某些3阶交互效应相混杂，某些2阶交互效应可能与其他2阶交互效应相混杂。

分辨度为Ⅴ的设计：某些主效应可能与某些4阶交互效应相混杂，但不会与3阶或更低阶交互效应混杂；某些2阶交互效应可能与3阶交互效应相混杂，但各2阶交互效应之间没有混杂。

以下依此类推，但常用的达到分辨度为Ⅴ的设计就可以了。

如果能够认为3阶及3阶以上的交互作用全都可以忽略不计，则与3阶及3阶以上的交互作用相混杂的因子效应或交互效应则称为是可估计的（estimable）（也称是纯净的（clear））。由此可知，分辨度为Ⅳ的设计中各主效应都是可以估计的，所有相互间并未混杂的2阶交互效应也是可估计的；分辨度为Ⅴ的设计中，全部主效应及全部2阶交互效应都是可估计的。

13.4.1.4　部分因子试验的设定

怎样才能根据k和p的数值确定分辨度的数值呢？这是个很难给出一般结论的问题，也没有简单的公式可用。统计学家为便于大家使用，就编制了计算分辨度的表格（见表13—20），学会使用这个表非常重要。下面举例说明计算分辨度及安排试验的方法。

表13—20　部分因子试验分辨度表

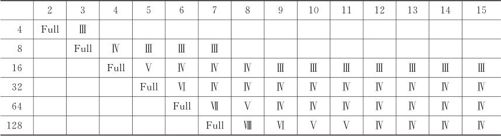
表13—20给出了在因子总数及试验总次数给定情况下所能达到的最大分辨度。表中，第一行代表试验的因子个数，第一列代表试验的总次数（不含中心点），表中所列出的数值就是最佳设计所具有的分辨度值。例如，第一行选因子个数为6，第一列选试验总次数16（安排全因子试验可以安排4个因子），这就是部分因子设计2^6－2。表中所对应的就是最佳设计所具有的分辨度值Ⅳ，也就是说我们可以使用设计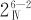。至于如何选定生成元，全部的定义关系（字）是什么，哪些效应间会产生混杂，这些都将由计算机自动给出，详细使用方法见13.4.2节。除非设计者有特别要求，由计算机所给定的设计通常是合用的、最好的。

表13—20还可以有更多的用途。例如，要考察8个因子，做多少次试验可以保证分辨度不低于Ⅳ？从表中对应因子数为8的那列可以看到，做16次或32次试验分辨度都是Ⅳ，做64次试验分辨度才能达到Ⅴ。这样一来，我们就可以决定，做16次试验就够了。再例如，如果条件限定最多做16次试验，如果保证分辨度不低于Ⅳ，最多可以安排多少因子？从表中对应试验次数为16的那行可以看到，安排6，7，8个因子都可以使分辨度为Ⅳ，故最多可以安排8个因子。

13.4.2　部分因子试验的计划

如何安排部分因子试验是很重要也是很细致的工作。过去安排因子时，主要是查有关的统计书籍或专门的正交表，但有了计算机之后，特别是MINITAB等软件给出的方案比一般的资料上所介绍的正交表种类要更多、考虑得更全面，计算机提供了默认生成元的设计方法，使用这种方法比较简单。如果此种办法能够满足要求，当然是最省事的。如果此种办法不能满足要求，则要自己选择生成元，而且事先要计算好设计方案，这就比较麻烦。

13.4.2.1　默认生成元的部分因子试验计划

我们通过一个例题说明如何安排部分因子试验。

例13—12

用自动刨床刨制工作台平面的工艺条件试验。在用刨床刨制工作台平面试验中，考察影响其工作台平面光洁度的因子，并求出使光洁度达到最高的工艺条件。

共考察6个因子：

因子A：进刀速度，低水平1.2，高水平1.4（单位：mm／刀）

因子B：切削角度，低水平10，高水平12（单位：度）

因子C：吃刀深度，低水平0.6，高水平0.8（单位：mm）

因子D：刀背后角，低水平70，高水平76（单位：度）

因子E：刀前槽深度，低水平1.4，高水平1.6（单位：mm）

因子F：润滑油进给量，低水平6，高水平8（单位：毫升／分钟）

要求：连中心点在内，不得超过20次试验，考察各因子主效应和2阶交互效应AB，AC，CF，DE是否显著。

解　由于试验次数的限制，我们在因子点上只能做试验16次，另4次取中心点，这就是2^6－2＋4试验。由表13—20可以查得，这时R＝Ⅳ，可达分辨度为Ⅳ的设计。各主效应间没有混杂，主效应与2阶交互效应间也没有混杂，但某些2阶交互效应可能与其他2阶交互效应相混杂，因此，只要保证所要考察的2阶交互效应AB，AC，CF，DE之间没有相互混杂就行了。

图13—37　部分因子设计的创建设计操作1

下面具体生成试验设计表。从“统计＞DOE＞因子＞创建因子设计（Stat＞DOE＞Factorial＞Create Factorial Design）”入口可得图13—37的左半图所示界面。

单击“显示可用设计（Display Available Design）”就可以看到图13—37右半图的界面。从图中的右半部分中的显示可以看出，这就是表13—20的内容，可以确认：用16次试验（不包含中心点）能够达到分辨度为Ⅳ的设计。

在图13—37左半部分，打开“设计（Design）”，可以得到图13—38右半图所示界面。

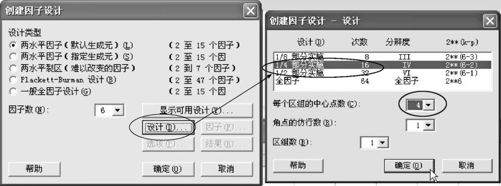
图13—38　部分因子设计的创建设计操作2

选中试验次数为16，再选中“中心点”为4个，点击“确定”，则可回到图13—39左半图所示界面，这时各选项如“因子”、“选项”“结果”等皆由灰色转为黑色了（见图13—39左）。

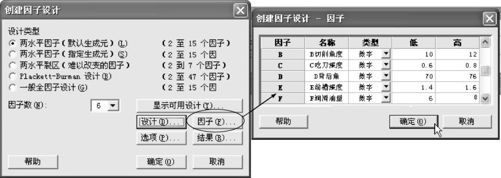
图13—39　部分因子设计的创建设计操作3

打开“因子（Factors）”，可以得到图13—39右半图界面，设定各因子名称，并设定其“高”、“低”水平值。点击“确定”后，回到图13—39左半图界面，再点击“确定”便可完成设计，得到试验计划表（见表13—21）。

表13—21　刨床工艺条件部分因子设计计划表

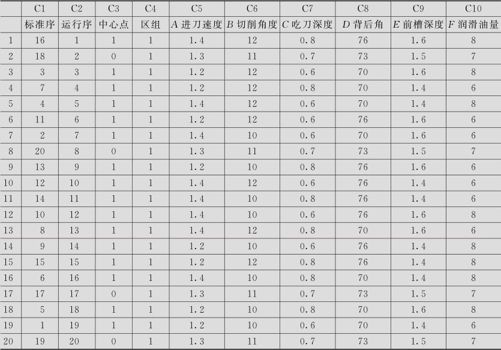
与全因子设计不同的是，我们不能肯定这个试验计划表一定能满足要求，因为部分因子试验中一定会出现混杂，这些混杂如果破坏了试验要求，则必须重新设计，而全因子设计则没有这个问题。从运行窗中可以看到下列结果：

设计生成元：E＝ABC，F＝BCD

别名结构

此表告诉我们，计算机自己选择的生成元（Design Generators）是：E＝ABC，F＝BCD。后面的“别名结构（Alias Structure）”中列出了交互作用项的混杂状况，即每列中互为别名的因子有哪些。在此结构表中的每一行，实际在正交表中相当于每一列，例如因子A所在列，由于表中显示：A＋BCE＋DEF＋ABCDF，这说明A所在的列，其实不仅A在起作用，同时起作用的还有BCE，DEF和ABCDF。有时也可将此式写成A＝BCE＝DEF＝ABCDF，表明这些项是互为别名的，或说它们是相互混杂的。当然，在这项中，除了因子A外，其他3项都是3阶或更高阶的交互效应，都可以忽略不计。如果此项效应显著，则可以断定是因子A效应显著，因此本列的混杂对我们分析因子A效应不会产生任何实质性影响。对于分辨度为Ⅳ的设计，关键是要检查一下我们所感兴趣的2阶交互作用的混杂情况。将3阶以上交互作用忽略不计，这里混杂的有：AB＝CE，AC＝BE，AD＝EF，AF＝DE，AE＝BC＝DF，BD＝CF，BF＝CD。本问题所要求估计的4个2阶交互作用是AB，AC，CF和DE，从别名结构表中可以看见这4项恰好没有重叠在同行。因此表13—21的试验计划是可行的。

万一出现“所要求的可以估计的2阶交互作用间在给定设计中出现混杂”，那该如何处理？这里有两种情况可能出现。一种是试验计划者可以自行解决的，其办法有两条：（1）将因子名称相互交换就可以自动解决；（2）自行选定设计生成元（这时就要改变计算机给出的缺省的生成元，自己另行指定）。还有另一种可能，那就是该问题所要求的那么多2阶交互作用不能与别的项混杂是根本办不到的。如何区分这两种情况比较复杂，通常可能需要向统计学家咨询。但是，不管遇到哪种情况，只要增加试验次数总是可以解决的。

13.4.2.2　指定生成元的部分因子试验计划

例13—13（续例13—12）

用自动刨床刨制工作台平面的工艺条件试验，6因子设定条件同上。要求是：连中心点在内，不得超过20次试验，考察各因子主效应和2阶交互效应AB，AC，CE及DE是否显著。

解　由于试验次数的限制，我们只能使用2^6－2＋4设计。但是从例13—12中的别名结构表中可以看出，AB与CE是混杂的，因此用默认的生成元来构造如表13—21这样的部分因子设计不能满足例13—13的需求。

我们先介绍一个运算性质：在解代数方程时，可以对等式进行变形处理，能使用的是各种“移项法则”，例如“等式左右两侧可以同乘相同的常数”等。这些法则对于带“≠”的式子同样成立。用这个法则实现生成元的设定是很有效的。

由要求条件可知，AB，AC，CE及DE不混杂，这相当于AB≠CE，AB≠DE，AC≠DE。

变形后可知，此即E≠ABC，E≠ABD，E≠ACD。从例13—11的方案比较中我们发现，分辨度为Ⅳ的设计生成元中，只能含3个字母（含4个字母就会像方案1那样变成分辨度为Ⅲ的设计）。而试验次数为16的各列中，字母个数为3的项只有4个：ABC，ABD，ACD及BCD。既然给定条件中有3个选择不可接受，因此，生成元只能选择E＝BCD。试验计划中对于F没有要求，因此F可以任选，我们取F＝ABC。

设定好了生成元，就可以使用自定义生成元形成试验计划表。其操作是：

从“统计＞DOE＞因子＞创建因子设计（Stat＞DOE＞Factorial＞Create Factorial Design）”入口（见图13—40左上）。这时要选“2水平因子（指定生成元）”，因子的个数填写“4”（这是基本设计的因子数，而不是总因子数“6”）。点击“设计”，打开后（见图13—40右上），选“全因子”；“生成元”项打开后（见图13—40下方），填写生成元的设定：E＝BCDF＝ABC。全部点“确定”后，就可以得到设计结果。

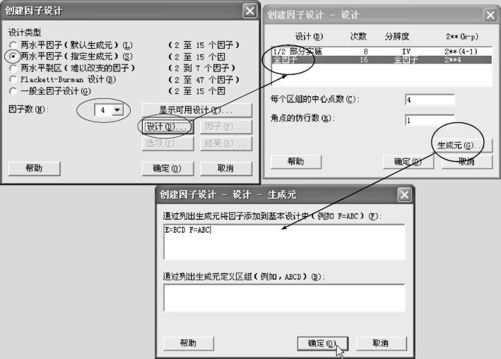
图13—40　指定生成元的部分因子设计操作

设计结果中的别名结构表如下：

设计生成元：E＝BCD，F＝ABC

别名结构

可以看出，AB，AC，CE及DE分别位于不同的列上，此设计满足了原定要求。总之，在计算机的帮助下，可以从别名结构表中验证选定的生成元是否能满足需求。

13.4.3　部分因子试验的实例分析

部分因子试验设计也是试验设计的一种，其分析方法当然应该与一般的试验设计的分析步骤相同，其流程图已列在13.3.3节。

由于部分因子试验分析方法与全因子试验分析方法基本相同，就不系统解释了。以下给出一个例子着重说明其与全因子设计的不同之处。

例13—14

降低微型变压器耗电量问题。在微型变压器生产的六西格玛改进中，经过头脑风暴发现，影响变压器耗电量的原因有很多，至少有4个因子要考虑：绕线速度、矽钢厚度、漆包厚度和密封剂量。由于绕线速度与密封剂量毫无关系，因而可以认为绕线速度与密封剂量间无交互作用。由于试验成本很高，研究经费只够安排12次试验。试验安排如下：

因子A：绕线速度，低水平取2，高水平取3（单位：圈／秒）

因子B：矽钢厚度，低水平取0.2，高水平取0.3（单位：mm）

因子C：漆包厚度，低水平取0.6，高水平取0.8（单位：mm）

因子D：密封剂量，低水平取25，高水平取35（单位：mg）

试验安排及试验结果列在表13—22中，响应变量是耗电量（单位：毫瓦）（数据文件：DOE_变压器（部分）.MTW）。

表13—22　变压器耗电量试验数据表

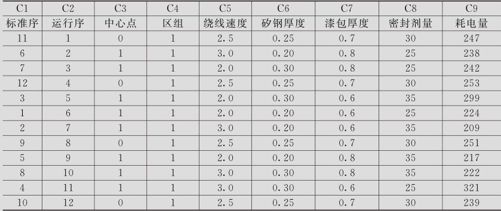
由于试验次数的限制，本例只能采用2^4－1＋4设计。由部分因子试验分辨度表（见表13—20）可以看出，8次试验（不包含中心点）可以实现分辨度为Ⅳ的计划。这时候，计算机自动取生成元D＝ABC，同时可知：AB＝CD，AC＝BD，AD＝BC，总计将有3对2阶因子效应相混杂。

对部分因子试验的数据进行分析，其方法与全因子试验设计的五步分析法完全相同。具体步骤及结果如下。

第一步：拟合选定模型

在MINITAB软件中，同样从“统计＞DOE＞因子＞分析因子设计（Stat＞DOE＞Factorial＞Analyze Factorial Design）”窗口进入，点击“项（Terms）”后，界面如图13—41右半部分所示。

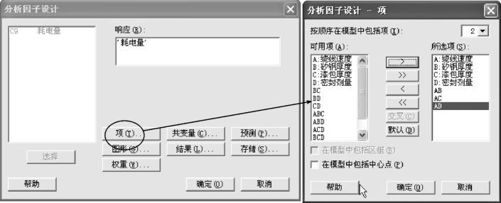
图13—41　部分因子设计的分析操作

由于现在是部分因子试验，“全模型”已不是包含全部交互作用项了。

点击“图形（Graphs）”后，在“效应图（Effects Plots）”中选“正态（Normal）”和“Pareto”；在“图中的残差（Residual for Plots）”中选“正规（Regular）”；在“残差图”中选“四合一（Four in one）”，在“残差与变量（Residual versus variables）”中，填写全部4个自变量名称。

点击“存储（Storage）”，在“拟合值与残差（Fits and Residual）”中选定“拟合值（Fits）”、“残差（Residuals）”及“标准化残差（Standardized residuals）”；在“模型信息（Model Information）”中选定“设计矩阵（Design matrix）”。

运算之后，从运行窗中可得到如下计算结果：

结果：DOE_变压器（部分）.MTW

拟合因子：耗电量与绕线速度，矽钢厚度，漆包厚度，密封剂量

耗电量的效应和系数的估计（已编码单位）

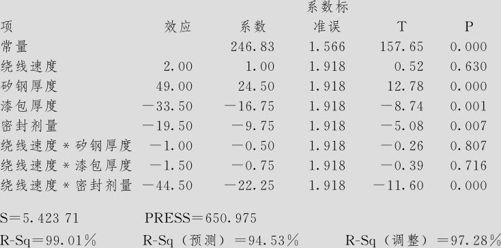
耗电量的方差分析（已编码单位）

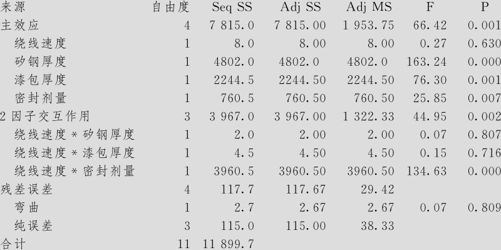
从ANOVA表中可以看出：模型总效应是显著的（主效应项p值＝0.001，2因子交互效应项p值＝0.002）；数据无弯曲（p值＝0.809）。回归效果的度量也很好，R-Sq＝99.01％，R-Sq（调整）＝97.28％。

从单个因子效应的检验可以看出：主效应中，因子A（绕线速度）效应不显著（p值＝0.630），因子B（矽钢厚度）效应显著（p值＝0.000），因子C（漆包厚度）效应显著（p值＝0.001），因子D（密封剂量）效应显著（p值＝0.007）。

分析交互效应要特别小心，计算结果显示A（绕线速度）与D（密封剂量）的交互效应显著（p值＝0.000）。但由于这里是部分因子试验，此项交互作用是由AD＝BC得到的，实际上可能交互作用AD显著，但也可能交互作用BC显著。根据例题的背景说明，实际上A与D不可能有交互作用，因此这项应该是BC的交互作用。当然，如果这一项效应是不显著的，则可以断言这二者都没有显著作用。

MINITAB计算中输出了效应的Pareto图（见图13—42），从图形窗中还可得到其他效应图、残差图等，此处从略。

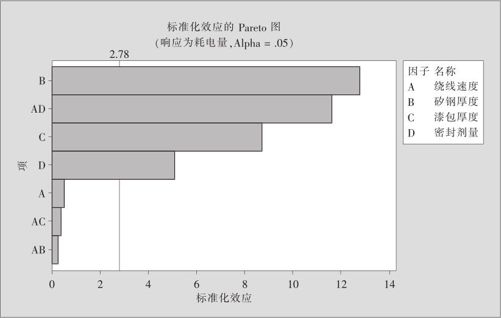
图13—42　部分因子设计效应的Pareto图

图形上同样显示是B，C，D及AD显著，但实际上应该是B，C，D及BC显著。部分因子试验的数据分析与全因子试验设计的数据分析相比较，其差别只在这里。即当数据分析结果中有某些2阶交互作用效应显著时，不能仅从表面上的结果来决定取舍，要仔细分析混杂结构，查看在别名结构表中，此显著项是与哪个（或哪些）2阶交互作用效应相混杂的，再根据背景材料予以判断，最终决定谁入选。如果没有相关背景材料提供，这时判断确实可能有困难，只好再做进一步的试验来区分这些混杂的交互作用。

第二步：进行残差诊断

残差诊断分析法与全因子试验设计完全相同。本例残差诊断中未发现任何问题，此处从略。

第三步：判断模型是否要改进

从残差诊断中看出，模型基本上是好的。从残差对响应变量预测值的图上也没看见非齐性状况，画出Box-Cox变换图也说明对y不用进行变换，也不需要增加x的高阶项。改进模型主要是删除不显著项。因此，实际上，又要返回第一步。

新第一步：拟合选定模型

结果：DOE_变压器（部分）.MTW

拟合因子：耗电量与矽钢厚度，漆包厚度，密封剂量

耗电量的估计效应和系数（已编码单位）

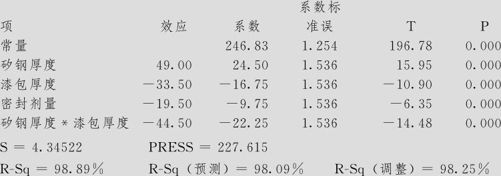
耗电量的方差分析（已编码单位）

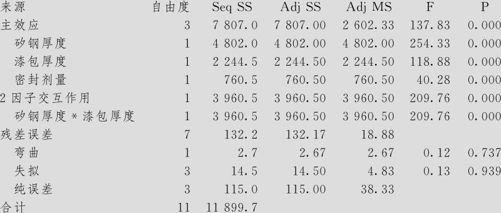
比较全模型与缩减模型的回归效果，各回归效果的度量见表13—23。

表13—23　部分因子试验模型拟合比较表

表13—23结果显示，删去不显著项后，模型确实得到了改进。

新第二步：残差诊断

从残差图上看，各残差图都正常，没有异常现象。

新第三步：判断模型是否要改进

已不需要改进了。

第四步：对选定模型进行分析解释

（1）检查是否有异常点。我们仔细查看原模型标准化残差的输出值，未看到有绝对值超过2的。

（2）输出各因子的主效应图和交互效应图。

从“统计＞DOE＞因子＞因子图（Stat＞DOE＞Factorial＞Factorial Plot）”进入，设置后即可得到主效应图和交互效应图。

主效应图见图13—43。

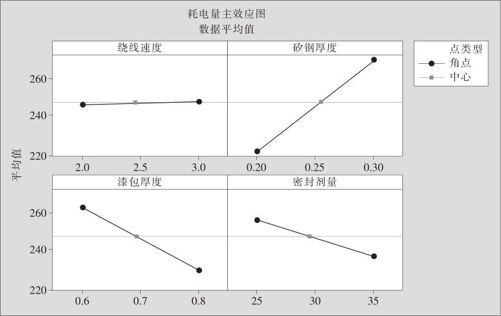
图13—43　变压器耗电量主效应图

交互效应图见图13—44。

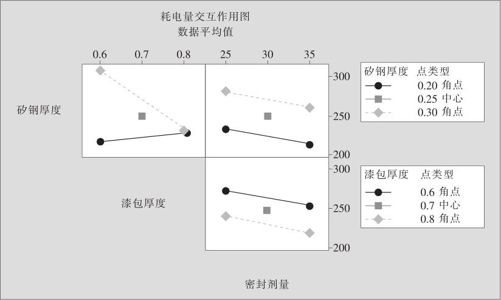
图13—44　变压器耗电量交互效应图

从图13—43主效应图中可以看出，因子B，C，D对于响应变量耗电量的影响确实是很显著的，而因子A的影响确实是不显著的。还可以看出，为使耗电量达到最小，应该让B尽可能小，C，D应尽可能大。

从图13—44中可以看出，因子B与因子C的交互作用对于响应变量耗电量的影响确实是很显著的（两条线非常不平行），而其他交互效应对于响应变量耗电量的影响确实是不显著的（两条线几乎平行）。由于B与C交互效应太大，因此要注意，单纯从主效应最优考虑的设置不一定是最好设置，因此还要从等值线图和曲面图来细致分析。

（3）输出等值线图和响应曲面图。

从“统计＞DOE＞因子＞等值线／曲面图（Stat＞DOE＞Factorial＞Counter/Surface Plot）”进入，等值线设置时，应选定密封剂量为35，等值线水平中选定数目为11，计算后即可得到等值线图及曲面图。等值线图见图13—45，曲面图见图13—46。

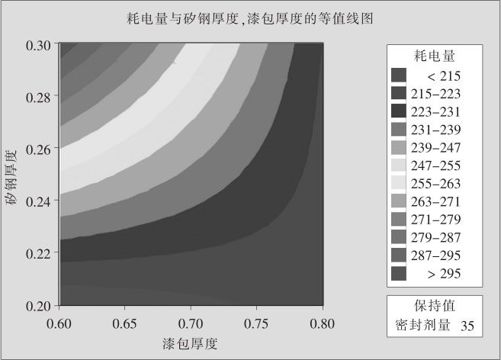
图13—45　耗电量对于B，C二因子的等值线图

图13—46　耗电量对于B，C二因子的曲面图

从图13—45中可以看出，其左下角比右下角更低，即因子B（矽钢厚度）应取最小值，因子C（漆包厚度）也取最小值反而更好些。这说明，仅从主效应图就判断最优值在交互效应强烈时不一定能选对。下面再看曲面图（见图13—46）。

从图13—46中可以看出，交互效应BC对于响应变量耗电量影响确实是太显著了（等高线很弯曲，曲面扭曲严重），为使耗电量取值更小，应该让B和C都取最小，D应取最大。

（4）实现最优化。

本具体问题是属于“望小”型的。从“统计＞DOE＞因子＞响应优化器（Stat＞DOE＞Factorial＞Response Optimizer）”入口。这时，在对最优的“目标（Goal）”选择上，取“望小（Minimize）”，在“设置（Setup）”中，只需填写“上限（Upper）”及“望目（Target）”两项，而“下限（Lower）”留为空白即可。我们取“上限”为“250”（这个值是在做过的试验中已经实现了的），取“望目”为“200”（这个值在做过的试验中未能达到，是较高理想）。计算机自动搜索后，得到最小值计算结果见图13—47。

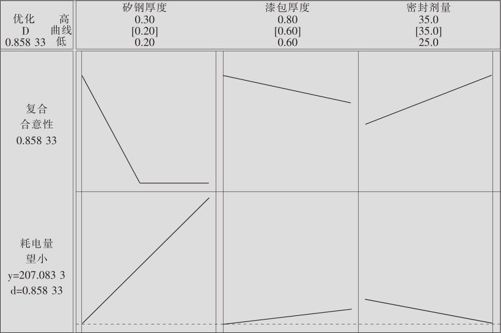
图13—47　耗电量的最优化结果图

从图中可知，当因子B（矽钢厚度）取最小值0.2，因子C（漆包厚度）取最小值0.6，因子D（密封剂量）取最大值35时最好，耗电量可以降至207.083。

大家可以看到，在试验过程中，进行第7号试验（标准序为2号）时，在A＝3，B＝0.2，C＝0.6，D＝35的条件下，曾经达到过耗电量209。在部分因子试验中，能够正巧在最优设置做过一次试验的这种情况（A不显著，取值无关大局）并不一定总能出现。由于是部分实施，有些试验条件的搭配组合并未做过试验。现在通过分析可以看到，即使未在最优设置处做过试验，我们的分析也可以预测到这个最佳设置。这正是试验设计统计分析方法的价值所在，如果只安排试验而不进行统计分析，是无论如何也做不到这一点的。

第五步：判断“目标是否已经达到”

本来，部分实施的因子试验的目的是筛选因子，能够由各因子的主效应图和交互效应图分析出哪些因子或哪些因子间的交互效应是显著的，应予以保留，这就达到目的了。如果目前的结果仍不满足要求，通常是以这些结果为依据，选定因子并确定因子水平，进行下一轮试验。例如，因子B（矽钢厚度）取比现最小值0.2更小些的值，因子C（漆包厚度）取比现最小值0.6更小的值，因子D（密封剂量）取比现最大值35更大的值来安排新一轮试验。如果目前的结果基本能满足要求，我们可以更充分地挖掘信息，进一步求出最佳值，甚至可以求出最佳值的预测值的置信区间。

从“统计＞DOE＞因子＞分析因子设计（Stat＞DOE＞Factorial＞Analyze Factorial Design）”入口，打开“预测（Prediction）”窗口，在因子设置数值中，依次输入“0.2”，“0.6”，“35”即可得到下列计算结果：

如果需要进一步计算m次（例如3次）验证试验平均值的95％置信区间，也与全因子试验设计的相应部分完全相同（参见13.3.3.5节），使用宏指令即可直接得到结果，此处从略。

13.4.4　Plackett-Burman设计

前面介绍的各种部分因子设计在一般情况下已经足够使用了。它的一般理论也比较完整，易理解，易应用。但有时试验经费非常昂贵，节省每一次试验都是有价值的，这时就可以使用试验次数更少些的方法。Plackett-Burman设计就是最常见的一种试验次数最少的另一类筛选因子设计方法。

如前所述，部分因子设计的试验次数n都是2的整方幂：4，8，16，32，…。这些试验计划保证了试验安排的正交性，除中心点外，任一列中正负号出现次数各占一半，任两列中，＋＋，＋－，－＋，－－四种搭配出现的次数都是相等的。这种正交性导致试验结果“均衡分散，整齐可比”。但是，保持正交性的设计其试验次数n是否非要是2的整方幂呢？数学上容易看出，n确实不一定非要是2的整方幂，但它一定得是4的整倍数。 Plackett-Burman设计就是对所有恰为4的整倍数的n的这些情况给出了设计。若此时n又恰为2的整方幂时，其结果与前面介绍的部分因子设计完全一样，因此没有讨论的必要。总之，Plackett-Burman设计最有用的是n＝12，20，24，…。我们常记Ln为试验次数为n的试验设计表，下面就是一个L12表（见表13—24）。

表13—24　Plackett-Burman设计表（n＝12）

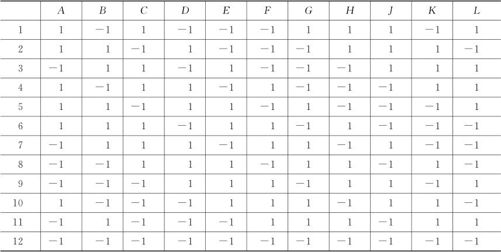
用Plackett-Burman设计来安排试验的最大好处是节省试验次数。例如用L12时，12次试验可以安排最多11个因子。当然，这种方法的分辨度只有Ⅲ，换言之，主效应将与2阶交互效应混杂。若任何一个2阶交互效应是显著的，则将导致不能准确分析主效应。这种设计不像一般的部分因子设计还可能提供别的更多信息，它只能用于筛选因子，因此也专称Plackett-Burman设计为“筛选试验设计”。它的使用范围和条件是：因子个数较多，试验费用昂贵，不必考虑任何交互作用。因此，不到万不得已，此方法通常是不采用的。

创建Plackett-Burman设计可以从“统计＞DOE＞因子＞创建因子设计（Stat＞DOE＞Factorial＞Create Factorial Design）”入口，选中第3行的“Plackett-Burman设计”即可。分析方法与前面介绍的部分实施因子设计完全相同，这里从略。

13.4.5　3水平部分因子试验的分析

对于全因子试验设计，本节前面只考虑了2水平试验的设计与分析。如果实际工作中确实需要考虑3水平或多水平时，可以自行定义一个全因子试验，计算机软件也有相应的设计与分析的功能。由于它与2水平的状况相仿，故不再加以叙述。如果需要进行3水平的部分因子试验时，就要自己动手安排和计算。

本来，高、中、低3水平的代码可以有多种选择方法，选1，2，3可以，选离散的A，B，C也行，但以连续型变量－1，0，1作为代码最好。这时，可以把对因子效应的方差分析和对自变量的回归结合起来进行。

下面举例说明。

例13—15

手机外壳注塑试验。为了提高注塑手机外壳的强度，研究影响强度的各因子的设置。为了考察如何能使其强度达到最大，要进行承载力试验，将外壳放入压力机中将其压碎，以其承载力（kg）为指标y，希望选定最优工艺条件使y达到最大。共有3个因子，选择其水平如下：

因子A（注射压力）（帕），A1＝500，A2＝520，A3＝540

因子B（注射时间）（秒），B1＝1.2，B2＝1.5，B3＝1.8

因子C（模具温度）（摄氏度），C1＝70，C2＝75，C3＝80

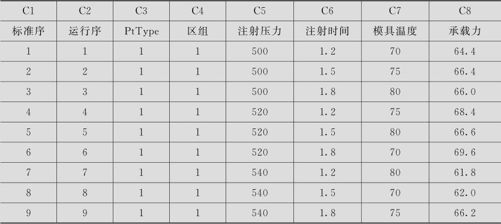
找出重要影响因子及最佳搭配，使承载力y达到最大。数据见表13—25（数据文件：DOE_手机壳（3水平）.MTW）。

表13—25　手机壳承载力数据表

解　3水平设计与2水平有很大差别，下面以本例做代表来说明整个设计及分析的操作过程。

在计划阶段，从“统计＞DOE＞因子＞创建因子设计（Stat＞DOE＞Factorial＞Create Factorial Design）”入口，选用“一般全因子设计（General Full Factorial Design）”，并选定因子个数为2（因为只进行9次试验），在对话窗“设计（Design）”中，填写A，B二因子，且水平数皆为3。在对话窗“因子（Factor）”中，填写A，B二因子各自的实际水平。在对话窗“选项（Options）”中，选中“非随机化”。这样就可以得到含A，B两因子各3水平的正交表。自己在表中再补充一列C，按部分因子3水平正交表的第3列填写，3水平仍取因子C的实际水平。随机化顺序后（本例题省略此步），就得到完整的试验计划表了（见表13—25前7列）。在实际试验后，将数据“承载力”填写在A，B，C因子列之后，就完成了数据的输入，结果见表13—25。

在分析时，不能使用“DOE”窗，而要从“统计＞方差分析＞一般线性模型（Stat-ANOVA-General Linear Model）”入口。这时，3个因子都应当作“固定效应”（因而不要填写入“Random Effect”窗内），得到ANOVA结果如下：

结果：DOE_手机壳（3水平）.MTW

一般线性模型：承载力与注射压力，注射时间，模具温度

承载力的方差分析，在检验中使用调整的SS

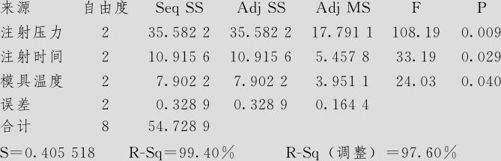
可以得知，3个因子的效应都是显著的（显著性水平取为0.05）。为了得到回归方程，要先在数据表中加上3个因子的平方项A—2，B—2，C—2，然后再进行回归分析。这是因为，因子取3水平后，不单有线性效应（Main Effect），而且包含2阶效应，不加入2阶项所得到的因子效应是不完全、不准确的。从“统计＞回归＞回归（Stat＞Regression＞Regression）”入口，选入A，B，C及它们的平方项共6项，结果如下：

回归分析：承载力与注射压力，注射时间，模具温度，A－2，B－2，C－2

回归方程为

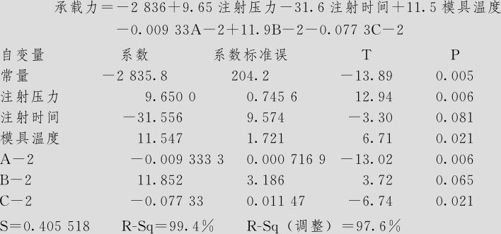
方差分析

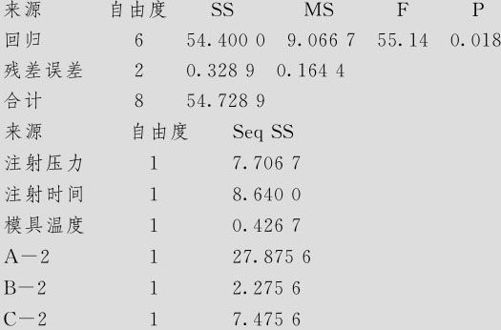
取显著水平为α＝0.10，则6项皆可以认为是显著的。

从“统计＞方差分析＞主效应图（Stat＞ANOVA＞Main Effect Plot）”入口，可以得到下列主效应图（见图13—48）。

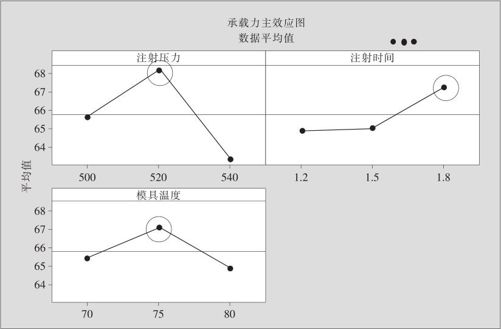
图13—48　承载力的主效应图

由图13—48可以断言，A取中水平520帕，B取高水平1.8秒，C取中水平75摄氏度，将使响应变量y取值最大。最后再从“统计＞回归＞回归（Stat＞Regression＞Regression）”入口，选定“注射压力”，“注射时间”，“模具温度”，“A－2”，“B－2”，“C－2”共6项，以“520”，“1.8”，“75”，“270400”，“3.24”，“5625”代入方程，得到最优值的预测结果如下：

新观测值的预测值

新观测值的自变量值

由上述结果可以看出，A取中水平520帕，B取高水平1.8秒，C取中水平75摄氏度，将使响应变量y取值达到最大值71.044。这个搭配是我们在试验中并未进行的。从方差分析的结果看到，3个因子中贡献最小的因子是C（模具温度），取A为中水平520帕，取B为高水平1.8秒，C只有取低水平70摄氏度的第6号试验，其结果为69.6，这是试验中的最好结果了，但我们的预报结果要优于此结果。可见我们的试验不但比全部搭配所需要的次数要少，而且可以预报出从未得到的好结果，再次证明统计试验方法的巨大威力。当然预报的结果要经过验证试验的确认才能最后判定为最优结果。