14.2　容差设计

产品设计可以分为系统设计、参数设计和容差设计三个阶段，或称三次设计。系统设计主要是用专业技术研制产品（即样品）及其生产工艺；参数设计是确定产品零部件的结构参数和生产过程的工艺参数，选择最佳的参数组合；容差设计是对各种参数寻求最佳的容许误差，使得质量和成本综合起来达到最佳经济效益。

过去，企业偏重于系统设计，对参数设计和容差设计缺乏足够的重视。现在，国内外研究表明，这种观念正逐渐改变，常常通过试验设计等统计技术来实现参数设计和容差设计。系统设计与各行各业的专业知识相关，不在本书的研究范围之内，而参数设计的内容已涵盖在本书的第13章中，本节将主要介绍容差设计（tolerance design）。

容差设计在完成系统设计和由参数设计确定了可控因素的最佳水平组合后进行，此时一般来说，各元件（参数）的质量等级较低，参数波动范围较宽。容差设计的目的是在参数设计阶段确定的最佳条件的基础上，确定各个参数合适的容差。容差设计的基本思想如下：根据各参数的波动对产品质量特性贡献（影响）的大小，从技术的可实现性和经济性角度考虑有无必要对影响大的参数给予较小的容差（例如用较高质量等级的元件替代较低质量等级的元件）。这样做，一方面减少质量特性的波动，提高产品的稳定性，降低质量损失；另一方面，由于提高了元件的质量等级，使产品的成本有所提高。因此，容差设计阶段既要考虑进一步降低在参数设计后产品仍存在的质量损失，又要考虑缩小一些元件的容差将会增加的成本，权衡两者的利弊得失，采取最佳决策。

通过容差设计，确定各参数的最合理容差，使总损失（质量损失与材料成本之和）达到最佳（最小）。我们知道，使若干参数的容差减少需要增加成本，但由此会提高质量，减少功能波动的损失。因此，要寻找使总损失最小的容差设计方案。

容差设计又常常与参数设计相辅相成。按照参数设计的原理，每一层次的产品（系统、子系统、设备、部件、零件），尤其交付顾客的最终产品都应尽可能减少质量波动，缩小容差，以提高产品质量，增强顾客满意度；但另一方面，每一层次产品均应具有很强的承受各种干扰（包括加工误差）影响的能力，即应容许其下属零部件有较大的容差范围。对于下属零部件通过容差设计确定科学合理的容差，作为生产制造阶段符合性控制的依据。虽然容差设计的实施一般晚于参数设计，但有时为了获取总体最佳，容差设计也会影响参数设计的再实施。

怎样才能有效地评估和优化产品的容差设计呢？具备六西格玛水准的容差设计是如何诞生的？下面将结合一个典型的机械系统设计案例，介绍容差设计的基本原理和MINITAB的实现方法。

例14—1

在一个装配环中装入3个零件，如图14—1所示，技术要求间隙（Gap）的目标值T＝0.015，LSL＝0.005，USL＝0.025，也就是Gap的长度要求满足0.015±0.010。加工的零件1，2，3的平均值μ_p＝1.554，标准差σ_p＝0.001，而装配环的平均值μ_e＝4.676，标准差σ_e＝0.002。假设所有部件的参数均已实现六西格玛的目标，试问：该系统此容差设计的能力如何？如果未能达到六西格玛水平，应当如何改进？

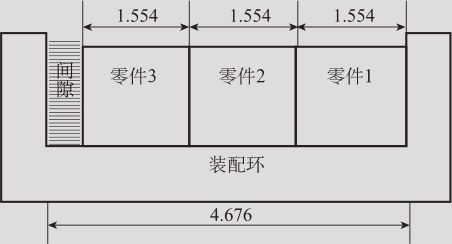
图14—1　机械装配设计实例

容易看出，间隙y与装配环（x₁）和3个零件（x₂₁，x₂₂，x₂₃，）的设计关系是

为了便于下文的分析说明，首先给定几个相关变量：

N_i——各部件数量；

V_i——各部件向量（取值为＋1或－1）；

W_i——各部件优化的分配权重（通常对于容易优化、成本低廉的部件分配权重较高，对于不易优化、成本昂贵的部件分配权重较低，但总和恒定为1，本例中假定装配环的分配权重W_e＝0.6，加工零件的分配权重W_p＝0.4）。

系统的现状为：

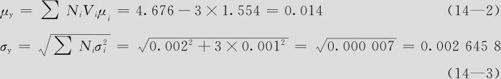
大于公差上限的不良率为：

小于公差下限的不良率为：

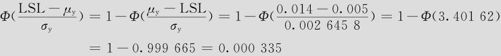
（这里使用了标准正态分布的计算公式Φ（－t）＝1－Φ（t），此公式以后还要用多次。）

总不良率为0.000016＋0.000335＝0.000351，即351ppm。

相应Z值为：

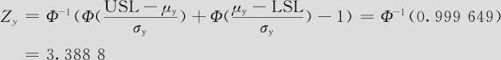
与Z目标值Z_y0＝4.5相比（即总不良率小于3.4ppm），该系统的容差设计能力仍然是不尽如人意的。

我们的设计尚未达到目标的原因有两方面：现在的均值μ_y＝0.014稍偏离公差中心（T＝0.015）；标准差太大。因此改进也有两种途径：调整均值或降低各部件的标准差。下面分别讨论。

1．调整均值μ_y。

从式（14—2）容易看到，要将μ_y＝0.014增大到μ_y0＝0.015，可以有两种途径实现：增加装配环的均值0.001；也可以减小三个零件的每个均值0.001/3。容易看出，这两种增大μ_y达到目标μ_y0的措施其效果是完全相同的。若将μ_y＝0.014增大到μ_y0＝0.015（这时过程均值已与公差中心重合），其标准差仍需降低，但调整均值可以显著改善不良率，且使降低标准差的任务减轻，具体计算见下文。

2．降低标准差σ_y。

如何根据不同的均值状况来确定各零件的标准差以使不良率降低到3.4ppm是容差设计的关键环节。按照六西格玛初始的要求，应该将标准差σ_y降低到半公差限的1/6，即要求σ_y0＝0.01/6＝0.001667。但实际上不用这样苛刻。事实上，由于要求σ_y0满足下述方程

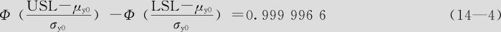
经过变形处理（详细推导见参考文献［29］，徐凌、马逢时的论文《六西格玛设计中的标准差计算》，即将发表），只需要σ_y0满足下列可直接计算的条件：

式中，R为半公差限（即R＝（USL-LSL）/2）；K是过程偏离指数（见本书12.6.1节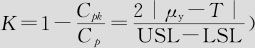，；L（K）的值可以查六西格玛容差设计标准差系数表（见表14—1，表的全文见书末附表13。那里K间隔更小，且有5位小数）。或用近似公式式（14—6）计算。

表14—1　六西格玛标准差系数表

（在式（14—6）中把K写成x）

在本例中，容易看出偏离指数为：

由x＝0.1，查表14—1或用式（14—6），可知，L＝5.0013，因此，σ_y0＝0.01/5.0013＝0.0019995就行了。需减少的方差为：

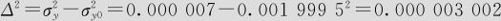
标准差Δ＝0.0017329

对于各部件，可用公式

求出新的符合要求的标准差。例如

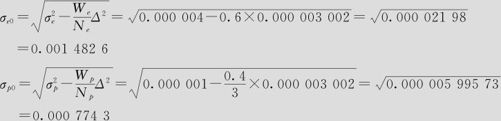
上述计算太烦琐，我们编写的MINITAB的宏指令可以很方便地完成上述计算。在调用宏指令前，我们先要把原始资料存入六西格玛设计的平台文件（数据文件：SS容差设计1.MTW），空白的平台文件见数据文件：SS容差设计.MTW。平台中的前5列是原始数据，C6～C8三列是使用时要先填写提供的；以后各列都是计算结果，在开始时皆为空白。使用时应先填写完成前5列（例14—1填写后的结果见数据文件：SS_容差设计1.MTW），其前5列之界面如下图（见图14—2）。这里，C1与C2两列构成设计目标变量（本例是“间隙”）的表达式（可以看出，本平台只限在目标变量是各零部件的线性函数情况下使用）。C3及C4是各部件原来的均值和标准差，C5给出目标变量（本例是“间隙”）的公差限。

图14—2　机械装配设计例初始数据显示图

下面给出宏指令的使用方法。

调用宏指令是从“编辑＞命令行编辑器（Edit＞Command Line Editor）”入口，在相应窗口中填写宏指令调用命令即可。本宏指令命令为：

％toldesign

本宏指令使用特别简单，输入上述名称后不用填写任何其他信息，然后单击“提交命令”就行了。计算后将给出C9～C17全部结果（见图14—3）。

图14—3　六西格玛设计平台界面图

公差设计平台的功能将根据“方差调整权”是否设定而分为下列两类：

（1）计算绩效功能。平台中的C6，C7是设定的各部件的均值及标准差，一旦C6，C7设定，再将设定方差调整权C8列全部设置为0，则可以根据给定的公差限，计算出目标变量低于下公差限的不良率、高于上公差限的不良率、总不良率及相应的Z值（C10～C14），相应的偏离系数K及标准差系数L。这时，计算机也将给出各部件的均值的调整建议（表达方式详细说明见后）及方差调整权建议（C15～C17）。

（2）计算标准差功能。根据设定的各部件的均值及标准差（C6，C7），加上设定的方差调整权C8，则可以计算出各部件的标准差调整建议。

因此，一般的六西格玛容差设计的使用步骤如下：

（1）研究各部件均值的调整。先将C6，C7设定为原始的各部件的均值及标准差（通常可以将C3，C4两列复制过来即可），将设定方差调整权C8列全部设置为0。这时调用宏指令将计算出目前不良率状况，同时给出各部件的均值的调整建议。

（2）计算出各部件方差调整权。根据（1）得到的均值调整建议，可以设定新的均值（填写入C6），而设定标准差C7及方差调整权C8不变。这时调用宏指令将验算均值是否调整到位；计算出调整均值后的不良率及Z值；同时计算出各部件方差调整权的建议。

（3）计算出各部件标准差应调整到的目标值。根据（2）计算出的各部件方差调整权建议，使用者可以根据各部件的性质、改进标准差需要的成本与难度，尝试给出可接受的各部件方差调整权，这时调用宏指令将根据设定方差调整权计算出各部件标准差调整建议。各部件方差调整权的设定可以逐步调整，不一定一次到位，也不一定要保证完全合适，更不一定满足成本最低原则。计算每次设置之值，计算机都会给出新的建议。

如果调整中出现问题（例如，按设定的方差调整权不可能找到标准差改进方案），计算机会给出出错信息。

（4）计算最终设计方案的效果。根据调整后的均值及标准差计算出最终的不良率及Z值。如果尚未达到满意水平，还可以继续调整均值、标准差，不断重新计算。

下面我们以机械零件装配间隙为例说明容差设计平台的使用方法。首先打开文件SS_容差设计1.MTW。

（1）调整均值。以最初的设计方案参与计算：将C3及C4的值复制到C6及C7，将方差调整权C8全部设置为0。调用宏指令

％ toldesign

这时可得计算结果如图14—3中C9～C17所示。在计算中首先得到了C11中的目前间隙的均值为0.014及C12列中的标准差0.0026458。以此为基础，容易计算出小于公差下界的不良率为0.000335，大于公差上界的不良率为0.000016，合计为0.000351，大约351ppm的不良率，其Z值为3.3888（注：当Z值达到4.5时就是达到6西格玛水平）。从C11列中看到，间隙的均值目前为0.014，而公差中心为0.015，未对准中心必然导致不良率较大，需要调整（增大）均值0.001才行。如何实现这一点？调整一项或多项变量几种方法都可以使目标变量对准中心。但容易理解，在正态分布的假定下，调整一项或同时调整多项变量以使目标变量对准中心，其结果其实是一样的。换言之，在众多项中究竟调整哪些项、不调整哪些项根本不用讨论，只要根据实际问题的状况来确定，任意选择某个（或某几个）变量调整就行。当然，一般来说，只调整一个变量最简单。我们在C15中给出了可能的选择，但要注意，调整时只能选择其中一个。例如我们选第一项装配环宽度，由4.676调整到4.677，其他项则要保持不动。

注意：如果只对某一项调整有困难，可以增加调整的项数。可先任意选择调整一项，不一定达到C15建议的值。这时可以先输入这一项调整结果，再次调用宏指令，计算机会自动计算出下一次需要调整的值（仍然是只能再调一项），以此类推。六西格玛设计的一个最简易原理就是最好要使均值能完全达到目标。众所周知，降低标准差不容易实施，且要增加成本；调整均值则更容易实施且不需增加成本，这当然是最好选择。

（2）下面计算调整均值后的效果。将在C6列内的装配环长度，由4.676调整到4.677，其他项不动，标准差（C7）及方差调整权C8为0维持不变。再次调用宏指令（注意：不改变宏指令内容而调用宏指令，可以使用快捷键Ctrl＋L及Alt＋S直接完成调用），得到下列结果（见图14—4）。

图14—4　六西格玛设计平台第二次计算结果界面图

可以看到，C11中的间隙均值已经调整到位，不良率最终已达到0.0001571，Z值升至3.60338。下一步的任务应该是设法降低方差。C14中的第5项K是过程能力指数中的偏离系数。C12中列出了目标：现在标准差已达到0.0026458，要达到六西格玛水平（即Z值为4.5），标准差应降低到0.0021528。C14中的第6项L是计算此值的依据，它表示的是半公差限相当于新标准差的倍数（本例是满足关系0.0021528＝0.010/4.6452）。当然，要实现这样的任务通常不能靠降低一项变量的方差就能实现。为此，计算机给出了改进建议，即把降低方差的目标按各自原来的方差大小“分配任务”，方差越大、重复数越多者权重越大。这样的建议当然仅供参考，使用者要根据自己的实际情况来考虑，要注意到各变量的实际波动状况，包括降低方差的成本等需要统筹考虑来确定。我们可以不断调试以达到最后目标。例如现在对于这两个变量分别给出建议，现在的权重总和恰好为1，调试中可以让权重取粗略些的值。如果取总和小于1的值，则通常达不到Z值为4.5的要求；如果总和大于1（相当于对Z值要求超过4.5），或某些项降低方差的任务过重，这将导致由于不能实现这样的高目标而由计算机给出“出错信息”。

（3）按调整权系数不断降低方差。降低方差的第一种方法是设定合适的调整方差权。宏指令给出了最初始的各项降低方差的权系数，即是以各项的方差（含系数）在总方差的比率为权。换言之，本项方差在总方差中占多大比率则本项在降方差中承担多大责任。具体写出就是：

在本例中，由于总方差为：

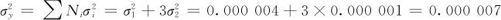
所以

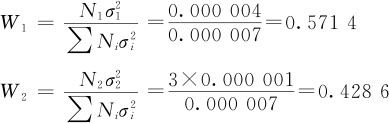
此权重建议列在图14—3中的C16中，二者分别为（0.57，0.43）。当然实际工作部门也可以根据该部件优化难易程度、改进成本等需求，给出生产部门方面的建议，例如本例简化为（0.6，0.4）。以此值（方案1）输入，计算结果如下（见图14—5）：

图14—5　机械零件装配间隙按权重方案1计算结果界面图

从图14—5看出，此权重方案可行，即各标准差可按C17所列各值予以改进。以C17列中各标准差的值回代入C7中，则可以得到最后结果（注意不要忘记将C8列全部设置改回为0），该结果显示于图14—6。

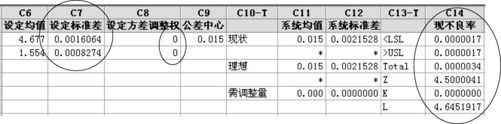
图14—6　机械零件装配间隙按方案1标准差值计算绩效结果图

可以看出，这时已经使Z值达到4.5，实现了六西格玛设计的要求。

（4）如果装配环均值调整有困难，是否可以只调整标准差而达到六西格玛水平？我们可以进行调试，这时假定方差的调整权仍为（0.6，0.4），其计算结果如图14—7所示。

图14—7　机械零件装配间隙按原均值方案2计算标准差结果图

按图14—7中C17的建议，可以计算出其绩效结果，计算时不要忘记将设定方差调整权C8全部设置为0，其结果见图14—8。

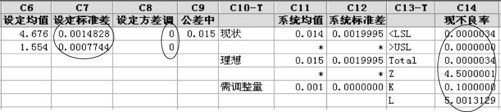
图14—8　机械零件装配间隙按原均值方案2标准差计算绩效结果图

可以看出，这时已经使Z值达到4.5，实现了六西格玛设计的要求。但比较图14—8（均值有偏）与图14—6（均值无偏），可以看出，如果能将均值调整到位，则可以得到图14—6所显示的更经济的方案。例如，将装配环的均值由4.676增加到4.677，则μ_y0＝0.015，这时过程均值已与公差中心重合。对于偏离指数为0的结果有L＝4.6452，因此整个系统的标准差σ_y0＝0.01/4.6452＝0.0021528就行了。同样用宏指令可以得到两个部件的标准差（见图14—5中C17），σ_e0＝0.0016064及σ_p0＝0.0008274，显然比均值未与公差中心重合时（见图14—7中C17）宽松些。

下面我们增加一个更复杂的例子说明六西格玛设计中的容差设计过程。

例14—2　气缸结构的六西格玛设计问题。

某汽车发动机的气缸由缸体、缸盖、活塞、活塞轴承、连杆、杆轴承和机轴装配而成（如图14—9所示）。目前气缸总装车间遇到的问题是，虽然各个零部件的机械尺寸都达到研发部门设计的规格要求，但总装在一起后总会有相当比例的成品装配过松或过紧，一次性通过率远远低于当初预定的目标，而且由此产生的返工造成大量额外的劣质成本损失，还影响出货进度。希望计算出能使总装达到六西格玛水平的各部件之均值及标准差。

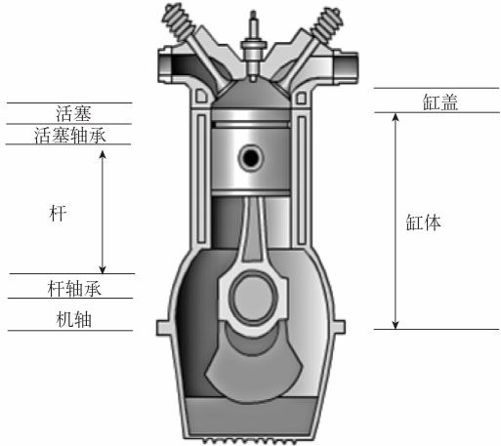
图14—9　发动机气缸的结构简图

在气缸总装的流程中，产品的质量特性是装配间隙，它的实际值可以通过下列公式计算：

装配间隙＝缸体＋缸盖－活塞－活塞轴承－连杆－杆轴承－机轴

最终的装配结果不能太松或太紧，也就是说必须将装配间隙的公差规格界定在一定的范围，如［0.005，0.015］之间。各个零部件的公差规格是这样的：缸体为8.49950±0.00468，缸盖为0.71000±0.00219，活塞为2.00050±0.00330，活塞轴承为0.25013±0.00114，连杆为5.00050±0.00327，杆轴承为0.20000±0.00099，机轴为1.75025±0.00249。

使用MINITAB宏指令，我们先填写完成前5列（例14—2填写后的结果见数据文件：SS_容差设计2.MTW）。其前5列之界面见图14—10，其中标准差是按公差限等于±3σ而计算出来的。

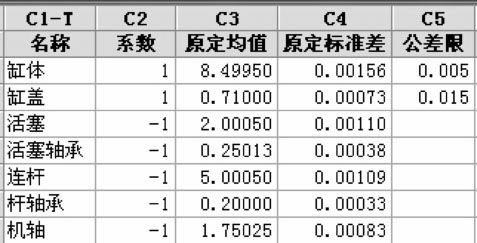
图14—10　气缸结构六西格玛设计平台界面图1

将C3，C4复制到C6，C7，将C8全部设置0，调用宏指令％toldesign后，可得计算结果如图14—11所示。

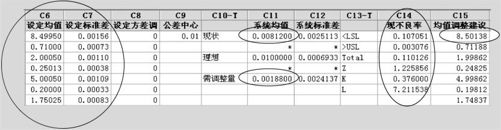
图14—11　气缸结构六西格玛设计平台界面图

间隙的均值为0.00812，标准差为0.0025113。以此为基础，容易计算出小于公差下界的不良率为0.107051，大于公差上界的不良率为0.003076，合计为0.110126，大约11％的不良率，其Z值只有1.225856。改进的办法是：

（1）调整均值。从图14—11中C11列中看到，间隙的均值目前为0.00812，而公差中心为0.01，需要调整（增大）均值0.00188才行。根据C15列的建议，我们可以选第一项缸体高度调整，由8.49950增大到8.50138，其他项不动。设定调整方差权C8维持为0不变。再次调用宏指令，得到下列结果（见图14—12）。

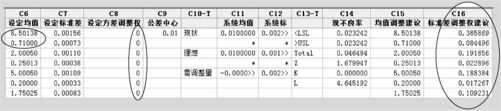
图14—12　六西格玛设计平台第二次计算结果界面图

可以看到，C11中的间隙均值已经调整到位，不良率最终达到0.0464838，Z值升至1.68。下一步的任务应该是设法降低方差。C12中列出了目标：现在标准差已达到0.0025113，要达到六西格玛水平（即Z值为4.5），标准差应降低到0.0010764。C14中的第6项L是计算此值的依据，它表示的是半公差限相当于新标准差的倍数（本例是0.0010764＝0.005/4.6452）。当然，要实现这样的任务通常不能靠降低一两项变量的方差就能实现。为此，计算机给出了改进建议，即把降低方差的目标按各自原来的方差大小“分配任务”，方差越大、重复数越多者权重越大。这样的建议当然仅供参考，使用者要根据自己的实际情况来考虑，要注意到各变量的实际波动状况，包括降低方差的成本等需要统筹考虑来确定。我们可以不断调试以达到最后目标。例如现在对于7个变量分别给出建议，现在的权重总和恰好为1，调试中可以让权重取粗略些的值，通常可以取总和小于1的值作为试验。如果总和严格等于1相当于一步达到六西格玛水平，我们可以逐步实现这样高的目标。

（2）按调整权系数不断降低方差。降低方差的第一种方法是设定合适的方差调整权，计算出各变量应达到的降低标准差目标。如上面第二次计算结果显示权重大体是（0.4，0.1，0.2，0.0，0.2，0.0，0.1）。以此值（方案1）输入，计算结果见图14—13：

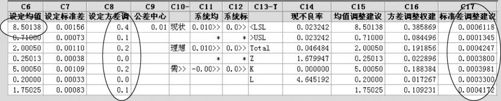
图14—13　六西格玛设计平台按权重方案1计算结果界面图

从图14—13看出，此权重方案可行，且各标准差应按C17所列各值予以改进。以C17列中各标准差的值再回代入C7中，则可以得到最后结果（注意不要忘记将C8列全部设置改回为0），该结果显示于图14—14。

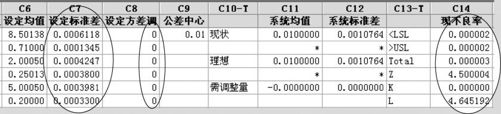
图14—14　六西格玛设计平台按权重方案2计算结果界面图

可以看出，这时已经使Z值达到4.5，实现了六西格玛设计的要求。

以下我们讨论在计算中可能出现的考虑以及按此计算的结果，供大家比较分析。

（1）有人建议，由于缸体的标准差最大，能否将其降低方差的权重上升为0.5，而且仅调整这一项（方案3）呢？这就是说，权重改为（0.5，0，0，0，0，0，0）。计算结果见图14—15。

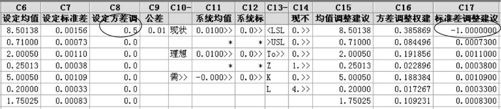
图14—15　六西格玛设计平台按权重方案3计算结果界面图

从图14—15中可以看出，C17显示方案3是不可行的。单靠降低缸体的标准差承担降低总方差一半的办法不能实现，方差调整权是不能随意主观设置的。

（2）有人建议，由于缸体的标准差最大，能否在均值调整到最佳值（缸体高度由8.49950调整到8.50138）后，将其方差降低一半实现六西格玛标准呢？这就是说，将缸体的标准差由0.00156降低为0.00078（方案4）？我们可以试算，结果列在图14—16中。

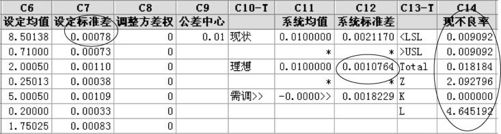
图14—16　六西格玛设计平台按权重方案4计算结果界面图

从图14—16中可以看出，在C14中显示方案4的效果是有限的。单靠缸体的标准差降低一半只能使Z值由1.68提高到2.09，此办法远不能实现达到六西格玛水平的目标。

（3）既然单靠缸体的标准差降低一半不能实现六西格玛的目标，让所有变量的标准差都减半如何（方案5）？

经计算后得到图14—17，从中可以看出，标准差全部减半的方案5将使总不良率降低到68ppm，Z值达到3.8，虽然尚未达到六西格玛的质量水平，但这样低的不良率仍然是令人鼓舞的好结果。

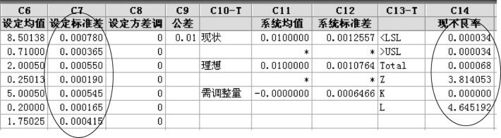
图14—17　六西格玛设计平台按权重方案5计算结果界面图

（4）由于调整均值可能很困难，有人建议缸体的均值只调整到8.501（均值仍然与公差中心有小偏离），这时是否能达到六西格玛水平？经过计算，这是可以实现的（方案6），但标准差要缩得更小（见图14—18）。注意，均值与公差中心完全重合时，总标准差只需要降低到0.0010764；现在均值与公差中心有偏离，总标准差要降低到0.0010255才行。

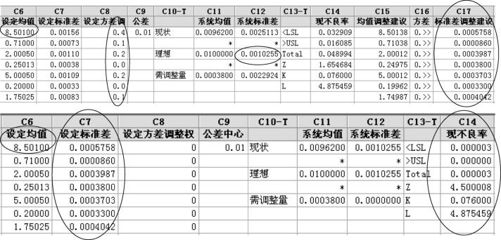
图14—18　六西格玛设计平台按权重方案6计算结果界面图

回顾一下我们对于公差设计平台的使用。平台使用的前提条件是：（1）目标变量是所有单个变量的线性函数；（2）每个单个变量都服从正态分布，且均值及标准差已经给定；（3）目标变量的目标应恰好为上下公差限的中点。公差设计平台的功能是两项：（1）计算功能。根据设定的各部件的均值和标准差及给定的公差限，计算出目标变量低于公差下限的不良率、高于公差上限的不良率、总不良率及相应的西格玛水平。（2）计算机将给出各部件的均值的调整建议及标准差调整权系数建议。反复使用，多次调整过程的均值及标准差参数，可以找到适合顾客需求及生产过程需求的最佳方案。

这里给出的宏指令功能是强大的，使用它可以代替原来的六西格玛设计软件，它可以一步到位地给出改进方案，也可以尽量多地考虑各方面情况，通过逐步调整实现改进计划。

总之，产品的容差设计中包含着这样的思想：从系统的最佳性能出发，确定部件的最优。用统计学的术语来说，就是首先考虑整体的最小方差，然后再考虑将每一部分的方差最小化。容差设计软件的普遍使用一定能够为企业的产品设计等工作带来巨大便利。