11.5　计数型测量系统分析

计数型测量系统的最大特征是其测量值是一组有限的分类数，如合格、不合格，优、良、中、差、极差，等等。前几节介绍的内容都是针对计量型测量系统的分析，当过程输出特性为计数型数据时，测量系统的分析方法会有所不同，一般可以从一致性比率和卡帕值两个方面着手考虑。

11.5.1　一致性比率

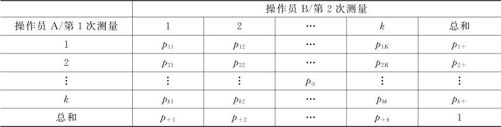
一致性比率是度量测量结果一致性最常用的一个统计量，它的计算公式可以统一地概括为：

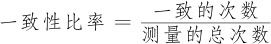
根据侧重点和比较对象的不同，又可以分为四大类。

（1）操作者对同一部件重复测量时应一致，这类似于计量型测量系统的重复性分析。每个操作者内部都有各自的一致性比率。

（2）操作者不但对同一部件重复测量时应一致，而且应与该部件的标准值一致（若标准值已知），这类似于计量型测量系统的偏倚分析。将每个操作者的测量结果与标准值相比较，又有各自不同的一致性比率。

（3）所有操作者对同一部件重复测量时应一致，这类似于计量型测量系统的再现性分析。操作者之间有一个共同的一致性比率。

（4）各操作者不但对同一部件重复测量时应一致，而且应与该部件的标准值一致（若标准值已知）。通常，使用这种一致性比率来衡量计数型测量系统的有效性。一般说来，一致性比率至少要大于80％，最好达到90％以上。当其值小于80％时，应采取纠正措施，以保证测量数据准确可靠。

接下来，用例11—5对计数型测量系统的一致性比率分析加以说明。

例11—5

某巧克力公司为检验新员工感官评估的培训效果，特取6块不同等级的巧克力请3位受训员工品尝并评分。试对此测量系统进行分析（数据列在表11—11中，数据文件：QT_MSA计数型量具.MTW）。

表11—11　巧克力评定结果

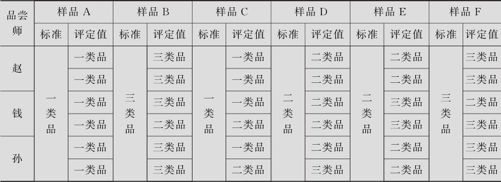
解　计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞属性一致性分析（Stat＞Quality Tools＞Attribute Agreement Analysis）”进入。

2．指定“属性列（Attribute Column）”为“评定值”，“样本（Samples）”为“样品”，“检验员（Appraisers）”为“品尝师”，“已知标准／属性（Known Standard/Attribute）”为“标准值”，运行命令后可以得到如图11—15所示的会话窗口输出和如图11—16所示的分析图形。

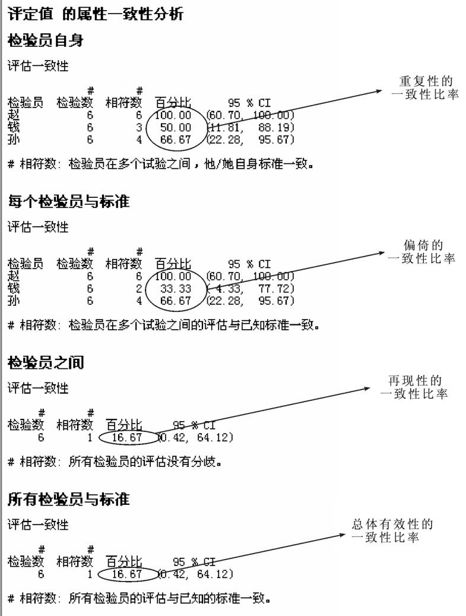
图11—15　一致性比率的分析结果

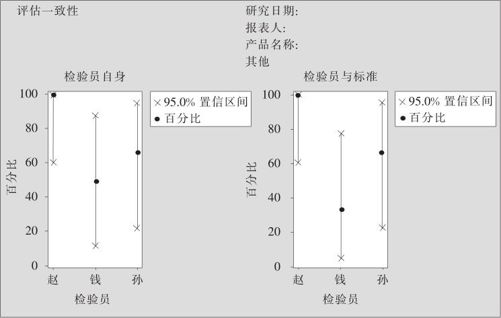
图11—16　计数型测量系统的分析图

图11—15分别显示了四类一致性比率的计算结果及其置信区间。容易看到小赵的评估水平最佳，小孙次之，小钱居末。整体而言，6个样品中只1个（样品A）测量完全正确，总体有效性的一致性比率＝16.67％≪80％，新员工培训效果仍然不能令人满意。为了保证测量数据的一致性，改进该计数型测量系统必不可少。图11—16是一张二合一的图形。其中左图是显示各品尝师重复性的区间图，右图是显示各品尝师偏倚的区间图，生动地展示了会话窗口中的计算结果。

11.5.2　卡帕值（κ）

κ（希腊字母，读音为kappa，中文为卡帕）是另一个度量测量结果一致程度的统计量，只用于两个变量具有相同的分级数和分级值的情况。表面上判别正确的比率P₀不能作为衡量一致性的标志，因为这里不能排除随机猜对的可能性。为此引入卡帕值κ，它的计算公式可以统一地概括为：

式中，P₀为实际一致的比率；P_e为期望一致（即随机猜对）的比率。κ在计算上有两种方法：Cohen的κ和Fleiss的κ。本文主要介绍的是比较常见的Cohen的κ，而Fleiss的κ与之基本相似。从式（11—25）可以看出κ肯定要比P₀小，它是扣除随机猜对可能性后的结果。

κ的可能取值范围是从－1到1，当κ为1时，表示两者完全一致；κ为0时，表示一致程度不比偶然猜测好；当κ为－1时，表示两者截然相反，判断完全不一致。通常，κ为负值的情况很少出现，表11—12归纳了常规情况下κ的判断标准。在计数型测量系统中研究一个测量员重复两次测量结果之间的一致性，一个测量员的测量结果与标准结果之间的一致性，或者两个测量员的测量结果之间的一致性时，都可以使用κ。

表11—12　计数型测量系统的合格标志

κ的计算原理大致上可以这样解释：表11—13表示某种产品共分k个等级数，两个操作员或一个测量员重复两次测量同一样品后，各种不同结果的概率分布情况。

表11—13　评定结果

在表11—13中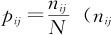，表示该结果出现的次数；N表示总的测量次数）。

根据概率论知识，容易推导得到：

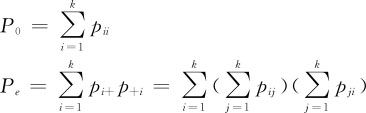
将P₀和P_e代入κ的定义式（11—25），就能够得到κ值。

接下来，用例11—6对计数型测量系统的κ值分析加以说明。

例11—6

某壁纸制造商为调查顾客对本公司产品色彩的评价是否一致，有意挑选了10个比较容易混淆的蓝色或绿色的样品，请两位顾客鉴定其色彩，试用κ统计量做再现性分析（数据列在表11—14中，数据文件：QT_MSAkappa.MTW）。

表11—14　色彩鉴定结果

解　计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞属性一致性分析（Stat＞Quality Tools＞Attribute Agreement Analysis）”入口。

2．指定“属性列（Attribute Column）”为“色彩”，“样本（Samples）”为“样品”，“检验员（Appraisers）”为“顾客”。

3．选择“选项（Option）”，确认“如果适当，计算Cohen的kappa（Calculate Cohen's kappa if appropriate）”被选中；选择“结果（Results）”，确认“控制结果显示（Control the Display of Results）”中的“此外，kappa和Kendal（顺序数据）系数（In addition，kappa and Kendal's (ordinal data) coefficients）”被选中，运行命令后可以得到如图11—17所示的会话窗口输出。

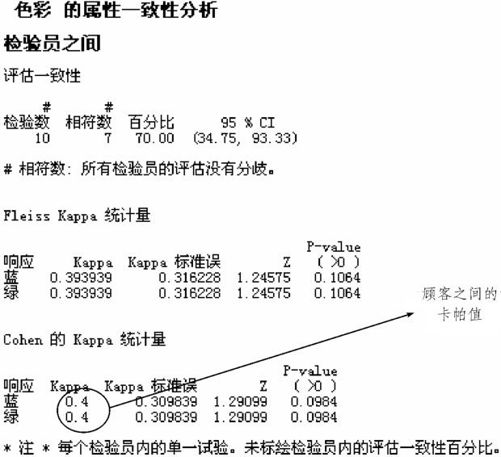
图11—17　卡帕值的分析结果

图11—17显示了Cohen的κ值为0.4＜0.7，表示不同顾客之间的再现性较差，也就是说两个测量员的测量结果之间的一致性较差。

下面解释这里κ值的计算步骤。根据表11—14中的数据，可以整理成一个表格（见表11—15）。在总共10件产品中，A，B一致认为是蓝色的有3个；A，B一致认为是绿色的有4个；A认为是蓝色、B认为是绿色的有2个；A认为是绿色、B认为是蓝色的有1个。其中有7件产品二人判断是一致的（左上到右下的对角线上的两格），直接计算一致率似乎应该是7/10＝0.7，但此数值并不准确，因为这里不能排除有“瞎蒙”的部分。A总共选了5个蓝，B总共选了4个蓝，如果二人在10件中随机选蓝绿，则凑巧选中同件产品的概率为0.4×0.5＝0.2，总计10件产品中，期望应为10×0.2＝2，此数列在表11—15中以括号显示。熟悉列联表的读者可以发现，表11—15中期望数值的计算与列联表中的期望计算是完全相同的。总计10件产品中，二人瞎蒙判断凑巧相同者期望共有5件（左上到右下的对角线上的两格带括号的数字之和）。带入κ计算公式（11—25），表面正确率P₀＝7/10＝0.7，瞎蒙正确率P_e＝5/10＝0.5，故有

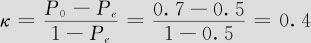
从κ计算公式中可以看出，如果A，B真的全部判断一致，P₀＝1，这时κ＝1；如果A，B判断水平与瞎蒙一致，P₀＝P_e，这时κ＝0。因此κ扣除了“瞎蒙”的成功，因而计算出的“一致率”比“表面一致率”稍小些，但反映一致性更准确。

表11—15　κ系数计算表

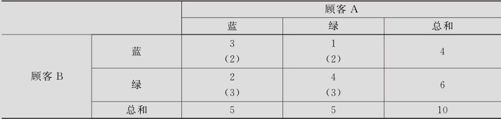
值得一提的是，如果将“顾客B”改为“标准答案”时，结果表示的就是一个测量员的测量结果与标准结果之间的一致性。