8.3　直线拟合的耐抗线方法

在六西格玛管理中，要寻求过程的改进，常常需要讨论两个变量间的关系问题。如果已经获得了n个观测值数对（x₁，y₁），（x₂，y₂），…，（x_n，y_n），我们希望能够拟合一条直线，传统的方法是使用最小二乘法估计出下列线性回归方程中的系数a及b。

但最小二乘法是不耐抗的，常常受到异常观测值的巨大影响，数据中的一个野值将导致最终回归方程结果完全失去意义。EDA就是希望能找到对异常值具有耐抗性的方法以使直线能很好地拟合数据。下面介绍的耐抗线方法即可解决此问题。很多统计学家建议在使用最小二乘回归之前先拟合耐抗线，以确定两个变量间的关系是否为线性，如果确认二者关系不是线性的，则希望找出将关系线性化的重建表达式，可以使用变换方法使之线性化，并且在拟合中能够识别出异常值。

8.3.1　耐抗线的基本原理与方法

本节先介绍耐抗线（resistant line）方法的基本原理及计算方法。

为了保证求出的回归方程（8—11）具有耐抗性，就要设法在求系数时舍弃观测值中可能出现的异常值。我们用下列五个步骤实现这一目标。

1．形成三个组

将数据按自变量由小到大的顺序分成样本量大体相等的三组：左组（L）、中组（M）及右组（R）。由于数据的总个数n不一定恰好是3的整倍数，因此不一定能分成样本量完全相等的3组。下面给出在n取不同值时的准确样本量（见表8—2）。

表8—2　耐抗线分析的数据分组表

例如，当n＝18时，则左、中、右三组皆含6个数据；当n＝19时，则左、中、右三组各含6，7，6个数据；当n＝20时，则左、中、右三组各含7，6，7个数据。

2．计算出各组的总括点

对于划分好的3个组，分别求出各组的中位数，记号如下：

这里要注意，我们可以用式（8—12）给出的这3对数据当作坐标而描绘出3个点，但这3个点并不是真实观测点。

3．形成拟合直线方程的初始估计

考虑如下形式的拟合直线方程：

此方程中，b就是斜率（slope）；a代表了在中组总括点处回归线的纵坐标，称为“水平”（level）。以式（8—12）中3个数对的数值来拟合方程（8—13）时，我们选定这样一对回归系数，将其作为a，b的初始估计：

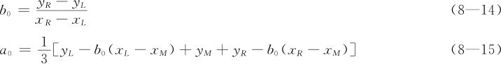
其实这里相当于要求左右两总括点都在此回归线的同侧，其残差相同，而且三个总括点形成的残差和为0。

4．求出对于初始回归方程的残差

考虑所有数据（x_i，y_i）对于如下直线方程：

的残差，记为。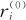

5．迭代修正求出最佳回归方程

以数据对（x_i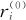，）为基础，按上述第2、第3步，求出式（8—13）的回归方程，我们把按式（8—14）及式（8—15）得到的回归系数分别记为δ₁及ε₁，然后以这两个系数修正原来的回归系数，其修正公式为：

以系数（a₁，b₁）返回步骤4及步骤5，可以得到新的回归系数（a₂，b₂），依此类推，不断迭代，直到系数修正之绝对值小于某个指定下界时，修正结束。

通过上述步骤所得到的回归方程很可能与传统的最小二乘法结果有很大差别，而耐抗线方法的结果将最大限度地以数据主体部分作为估计回归系数的依据，因而避免了可能的异常值对回归方程的灾难性的不良影响。

8.3.2　耐抗线方法实例分析

下面通过一个实例介绍根据数据求出耐抗线的具体步骤。

例8—2

某小学收集了18名儿童的年龄（以月龄计）及身高（以厘米为单位）的数据。数据列在表8—3中（数据文件：EDA_儿童身高.MTW）。希望找到身高与月龄间的关系。

表8—3　儿童月龄身高数据表

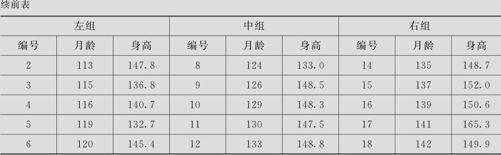
由于样本量为18，恰好为3的倍数，这里正好分为左、中、右三组都是6个观测值。对各组求出其中位数作为总括点，其月龄与身高数据见表8—4。

表8—4　儿童月龄与身高总括点数据表

我们画出散点图（见图8—10）。图中可以看到，在右组内有两个点很特殊，相对于其月龄而言，其中一个儿童身高太低，另一个儿童身高太高。

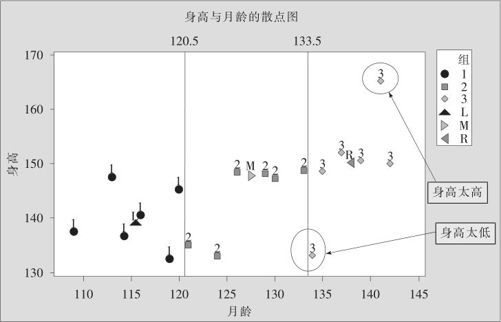
图8—10　儿童身高数据的散点图

将数据代入式（8—14）及式（8—15），可以得到初始EDA回归方程，其示意图见图8—11。这里要注意，此线只考虑三组的总括点的数据，由于总括点并未考虑异常观测值的数值，因而此回归线也丝毫未受到异常观测值的影响。

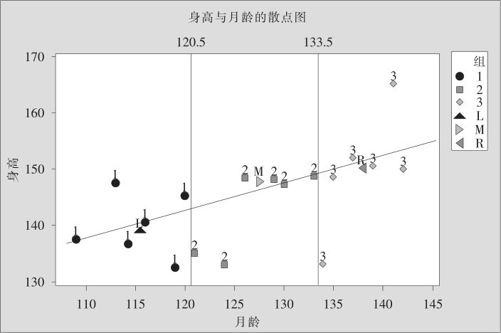
图8—11　儿童身高数据的初始EDA回归线图

具体数据结果说明了上述这一点：

EDA初始回归方程为：

身高＝146.01＋0.4933（月龄－127.5）＝83.11＋0.493 3月龄

最小二乘法回归方程是：

身高＝144.89＋0.5113（月龄－127.5）＝79.7＋0.511 3月龄

这里最小二乘法回归方程明显受到第17号观测点（身高特高者）的影响，斜率偏大。

EDA的初始方程再经过迭代调整，斜率逐渐降低，直到最后降至最小，得到EDA的耐抗线结果为：

身高＝145.65＋0.42857（月龄－127.5）＝91.007＋0.4285 7月龄

MINITAB可以直接实现上述全部过程。从“统计＞EDA＞耐抗线（Stat＞EDA＞Resistant Line）”入口，在“响应（Response）”中填写入“身高”，在“自变量（Predictor）”中填写入“月龄”，并要求存储残差、拟合值及系数，即可得到下列结果及图8—12：

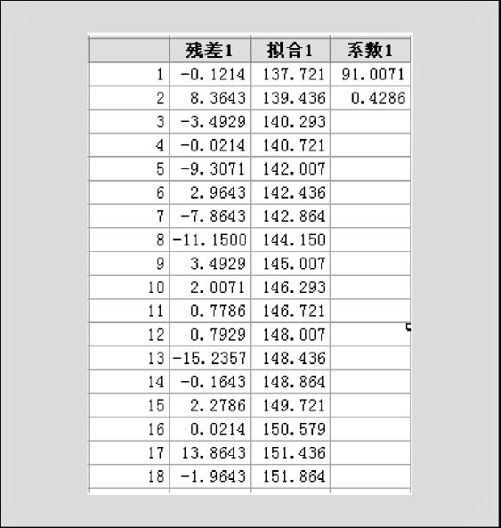
图8—12　儿童身高数据的耐抗线结果

耐抗线拟合：身高与月龄

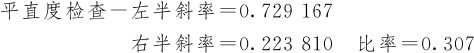
斜率1＝0.493333

斜率2＝0.422815

斜率3＝0.428571

斜率＝0.4286　水平＝91.0071　半斜率比＝0.307

在运行窗输出的结果中，有“左半斜率（Left-Half Slope）”和“右半斜率（Right-Half Slope）”。它们是根据左（或右）半侧的数据用总括点的数据估计出来的斜率值。

“比率（Ration）”则是左右两半斜率之比值。

如果此数值越接近1，则表明数据与直线拟合良好；相反，如果此数值远离1（不论太大或太小），则表明数据与直线相去较远。

下面绘制出回归结果的图形（见图8—13），其中EDA耐抗线结果用实线表示，最小二乘法结果用虚线表示。可以看出EDA耐抗线的主要特点是其建立起来的回归方程，不会受到异常观测值的严重影响，避免了传统的最小二乘法对异常观测值的敏感性。图中，EDA耐抗线更多地考虑了数据的主体部分，而最小二乘法受到第5，7，8，17号观测点的较大影响，斜率明显偏大。

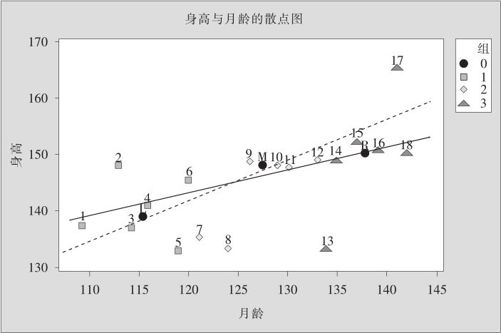
图8—13　儿童身高数据的耐抗线（实线）与最小二乘回归线（虚线）的比较图