6.1　单总体比率检验

我们常需要借助样本比率去判断总体中感兴趣的类别的比率变化，比如：了解改进之后，产品不合格品率比原来是否有显著降低（原有的不合格品率作为常量是已知的），顾客满意率是否比过去有显著提高（过去的满意率作为常量是已知的）等。这类问题通常可以通过单总体比率检验进行处理。

为叙述方便，设样本X₁，X₂，…，X_n来自两点分布总体X，记为X～b（1，p）。所谓两点分布就是，这里随机变量X只能取0或1两个数值，我们常规定：取1代表抽到不良品，取0代表抽到良品。记总体不良品比率为p，样本不良品比率为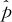，它可以由下式计算：

我们希望检验的假设是如下类型：

H₀：p＝p₀

H₁：p≠p₀

当然备择假设也可以换成“＞”或“＜”。

直接求出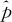的分布需要用到二项分布的概率计算，但当n较大时，即当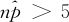且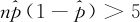时，二项分布可用正态分布去近似，因而有

这时可以用近似的Z检验对参数p进行假设检验。检验的统计量为：

当样本量较小时，计算机自动按精确的二项分布来计算，给出精确的p值。

在不同的假设下，在大样本情况时，显著性水平为α时的拒绝域如表6—1所示：

表6—1　比率p的显著性水平为α的检验

例6—1

小学生近视比率日益增加，现随机抽取了500位小学生进行视力检测，其中有310位近视，那么是否可以认为小学生近视比率已经超过六成？取α＝0.05。

解　（1）建立假设：

H₀：p＝0.6

H₁：p＞0.6

（2）因为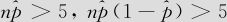，故可用近似Z检验；

（3）根据显著性水平α＝0.05及备择假设知拒绝域为{Z＞Z_1－α}＝{Z＞1.645}；

（4）由样本观察值，求得

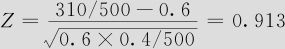
由于Z＝0.913＜1.645，样本观察值没有落在拒绝域中，因此不能拒绝原假设，即根据现有观测数据判断，小学生近视比率还不能说已超过六成。

应用MINITAB进行计算，从“统计＞基本统计量＞单比率（Stat＞Basic Statistics＞1 Proportion）”入口，界面如图6—1所示：

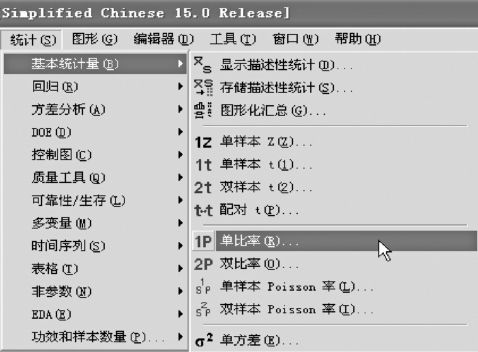
图6—1　单比率检验操作图1

如图6—2所示输入数据，要注意的是：图6—2右半部分若勾选“使用基于正态分布的检验和区间”，则求出的是近似结果，除非样本量足够大，一般不必选此项。

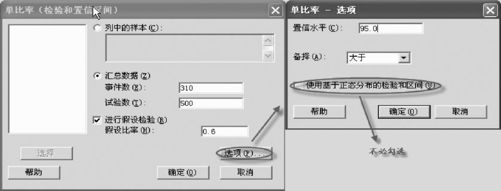
图6—2　单比率检验操作图2

本例中，没有勾选该项，可得到精确的计算结果：

单比率检验和置信区间

p＝0.6与p＞0.6的检验

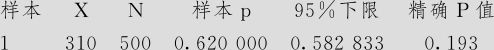
这里p值＝0.193＞0.05，因此不能拒绝原假设，即得到这样的结论：虽然小学生抽样数据近视比率达到0.62，但并没有显著超过六成。但当样本量增大10倍，相应近视人数也增大10倍时，对于同样的检验问题其检验结果就是显著的了。

单比率检验和置信区间

p＝0.6与p＞0.6的检验

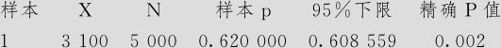
从上例也可以看出，要想从比率数据中获得显著性的结论，样本量要相当大才有可能。

作单比率检验时，一定要注意样本量的重大作用。上例中，两组数据样本比率都是0.62，但是310/500与3100/5000是有不同含义的。这也就是说，统计学不相信简单的百分数，一定要得知此百分数是从多大的样本量中获得的。比如，在本书前言中举的例子：去年本公司的顾客满意率为70％，今年调查了100个用户，其中75户表示满意，问：今年的满意率比去年有提高吗？对此问题，大多数人会毫不迟疑地说：“今年的满意率已经达到75％，当然可以说比去年的70％有提高了。”其实在学习了本段单比率检验后，用MINITAB软件算一下，就会立即发现这样回答不对。

建立如下假设：

H₀：p＝0.7

H₁：p＞0.7

运用MINITAB计算，其结果如下：

单比率检验和置信区间

p＝0.7与p＞0.7的检验

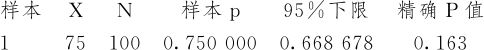
这说明：100个用户中，75户表示满意，并不能断言今年的满意率比去年的0.7有提高。

增大样本量后，会有些改进，其结果如下：

单比率检验和置信区间

p＝0.7与p＞0.7的检验

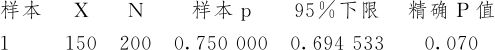
单比率检验和置信区间

p＝0.7与p＞0.7的检验

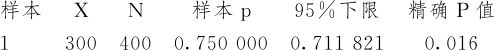
这说明：200个用户中，150户表示满意，也不能断言今年的满意率比去年的0.7有提高；直到400个用户中，300户表示满意，才能断言今年的满意率比去年的0.7有提高。

由于从比率数据中获得显著性的结论，样本量要相当大才有可能，因此，这也给我们以重要启示，在研究改进工作是否有效时，最好采用连续变量的度量，这样，宁可在度量时多花些时间和精力，这样在判断的时候，需要的样本量将要小得多；否则，采用离散变量的度量（只区分合格／不合格），当时可能省事，但需要进行比较时，则必须要有大得多的样本量，综合起来看不一定合算。

下面，我们可以复习一下如何求出单总体比率的置信区间问题。数据仍如例6—1给出，500位小学生中有310位近视，那么问题是：小学生患近视比率的95％置信区间是多少？

对于此类问题我们曾在4.3节中作过介绍，当时由于没学习过假设检验的思想，不能完全理解获得置信区间的原理。现在可以明白，要想获得比率的双侧置信区间，在图6—2左半部的选项“进行假设检验（Perform Hypothesis Test）”前面方框内，不要勾选（表示不进行假设检验），但要在图6—2右半部的“备择假设（Alternative Hypothesis）”中选择“不等于（Not Equal）”，这就可以获得比率的双侧置信区间；要想获得比率的单侧“大于型”的置信区间，只要在“备择假设（Alternative Hypothesis）”选择“大于（Great Than）”就可以；要想获得比率的单侧“小于型”的置信区间，只要在“备择假设（Alternative Hypothesis）”选择“小于（Less Than）”就可以了。

求小学生近视比率的95％双侧置信区间，只要在图6—2中右侧部分，将“备择假设”的“大于”换成“不等于”就可以得到下列结果：

单比率检验和置信区间

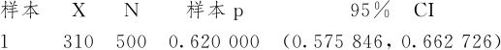
如果将数据增大到10倍，即5000名学生中3100名近视，则近视比率的置信区间就变成：

单比率检验和置信区间

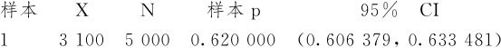
从上面两处不同样本量的比较中可以看出，样本量增大后，置信区间的宽度大大缩短了。