6.3　列联表与卡方检验

在前两节中，我们分别讨论了单总体和双总体的比率检验问题。当总体的个数增加到3个以上时，原来的方法就都失效了。本节所要介绍的列联表就是为了解决这个问题而引入的。但是列联表的功能要广泛得多，多总体比率检验只是其特例而已。列联表的检验要用到卡方检验（即用服从卡方分布的统计量作为检验统计量），但卡方检验不只用在列联表中，与此密切相关的还有另外一些离散型分布的拟合检验。本节将重点讨论下列三种假设检验问题：

（1）使用列联表进行因子间独立性检验；

（2）有限项离散型分布的拟合优度检验；

（3）分布的拟合优度检验。

由于这三种检验的检验统计量使用的都是χ²，因此统称这三种检验为卡方检验。

6.3.1　列联表

当数据资料以两种准则或者属性加以分类，那么所有的数据资料都可以归属于列联表。例如，因子A代表手机的不同品牌（分为四种：甲、乙、丙、丁），因子B代表顾客的不同满意程度（分三种：不满意、一般及很满意）。抽样调查可以得到相应的频数（例如，对品牌甲不满意者30人，对品牌甲感觉一般者40人，对品牌甲满意者62人等），我们可以利用收集到的数据组成列联表（如表6—4所示）。我们要进行的是对因子A与因子B是否独立进行检验，也就是检验顾客满意率状况是否与品牌有关。这就是两离散型因子间的独立性检验。

常见的列联表格式见表6—4。

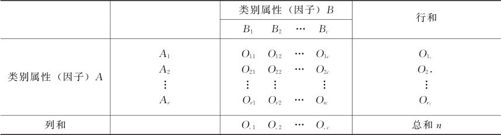
表6—4　随机样本的列联表

利用列联表进行独立性检验的步骤：

（1）建立假设：

H₀：因子A与因子B相互独立

H₁：因子A与因子B不相互独立

（2）确定检验统计量。抽取n个样本，归类整理如表6—4所示。其中O_ij表示第i行第j列中的观测数据，O_i.表示第i行数据之和，O_.j表示第j列数据之和，n表示数据总和。所以

如果列联表中两因子相互独立，则落入A_i与B_j格内之概率值p_ij必须满足p_ij＝p_i.p_.j，这里p_i.与p_.j表示由行和及列和分别求出的“边际”比率。这样我们最初设定的假设等价为：

H₀：p_ij＝p_i.p_.j

H₁：至少有一对i，j使p_ij≠p_i.p_.j

实际问题中，对于边际比率的估计可以简单地采用实际样本的比率来估计就行了，写成公式就是：

所以

而列联表中属于A_i行及B_j列交叉格的数据期望值为：E（O_ij）＝n×p_ij，因而其估计量为：

当实际观测值O_ij与期望值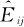相差不大时，可以认为因子A与因子B不相关，或相互独立；如果相差太大，就不能认为两因子无关了。按照这样的想法，我们选用统计量：

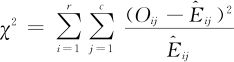
在H₀成立的条件下：

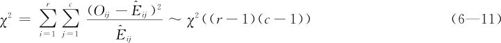
（3）显著性水平为α时的拒绝域为W：

式中，r是列联表的行数；c是列联表的列数。

下面用一个具体的例子来说明如何进行列联表的独立性检验。

例6—4

某连锁超市要检验商品销售情况与陈列方式是否相关，随机抽取了300家门市，它们将商品分别以A，B，C共三种方式陈列，并将各门市销售情况以“高”及“低”归成两类，如表6—5所示，数据是落入响应范围的门市部个数。

表6—5　陈列方式与实际销售情况数据表

问：在α＝0.05时，是否可以认为销售情况与陈列方式相互独立？

解　（1）建立假设：

H₀：销售情况与陈列方式相互独立

H₁：销售情况与陈列方式相互不独立

（2）确定检验统计量的值：

先由式（6—10）计算出各陈列方式期望的销售情况数值，如：

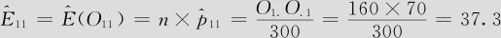
其他以此类推（参见表6—6）。

表6—6　各陈列方式对应的期望的销售情况数值

检验统计量为：

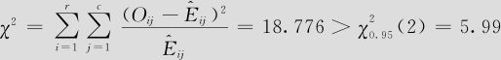
由于统计量值落在拒绝域中，因此拒绝原假设，即在α＝0.05水平上，可以断言销售情况与陈列方式不具有独立性，商品陈列方式会影响销售情况。

用MINITAB软件计算：

（1）当录入数据为列联表格式时。

打开数据文件“TBL_陈列方式.MTW”，依次选择“统计＞表格＞卡方检验（工作表中的双向表）（Stat＞Tables＞Chi-Square test（Table in worksheet））”，将列联表中各列（C2～C4）作为响应变量输入，如图6—4所示。可得下列结果：

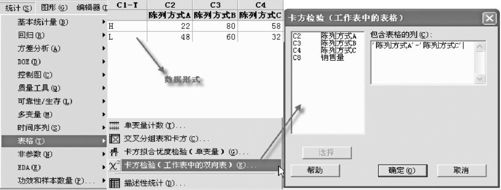
图6—4　卡方检验操作图（列联表格式）

卡方检验：陈列方式A，陈列方式B，陈列方式C

在实测计数下方给出的是期望计数

在期望计数下方给出的是卡方贡献

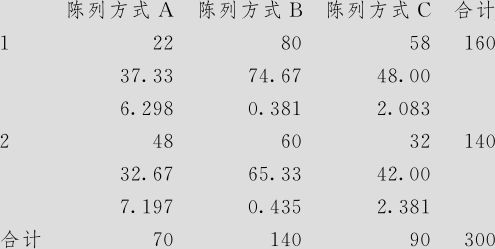
卡方＝18.776，DF＝2，P值＝0.000

这里p值＝0.000＜0.05，得到同样的结论：拒绝原假设，即在α＝0.05水平上，销售情况与陈列方式不具有独立性，商品陈列方式会影响销售情况。

（2）当录入数据按因子排列时。

这里指的是录入数据的形式是按因子排列的原始数据或是按因子排列的频数值格式。

请注意，表6—5给出的是整理好的列联表，两个因子分别处于“行”和“列”的位置。原始记录的记录方式则与此不同，其各个因子各占一列。此外，还有一种对原始记录稍加整理的统计计数格式，即按原有归类分别记录了其频数数据，其因子仍各占一列（见图6—5中的数据表）。比如例6—4，我们用C6记录“销售情况”，用C7记录“陈列方式”，不论C8列记录的是原始销售记录（购买者姓名记录）还是求了总数的频数记录，MINITAB都认为，只要各因子单独成为一列，就要先用交叉分组制表的方法将数据整理成列联表格式（两个因子分别位于“行”和“列”），然后再进行卡方检验。

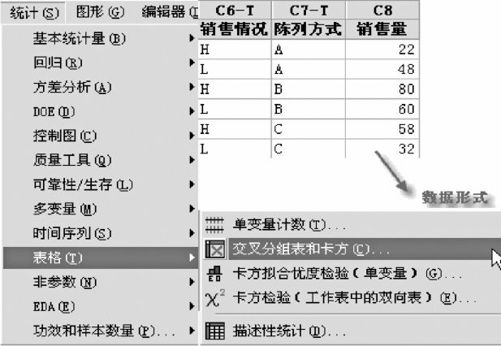
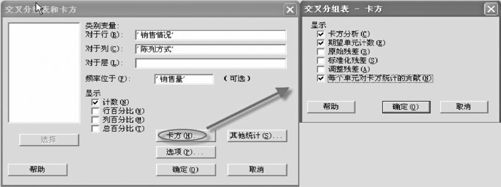
图6—5　卡方检验操作图（原始数据格式）

我们可以从“统计＞表格＞交叉分组表和卡方（Stat＞Tables＞Cross Tabulation and Chi-Square）”入口，将工作表中C6和C7分别作为“行”及“列”，将C8（销售量）作为频数输入（见图6—5）。

在未进行卡方检验前（即图6—5下左半部操作）后，只默认选择“计数”则可得到下面这个列联表：

列表统计量：销售情况，陈列方式

使用销售量中的频率

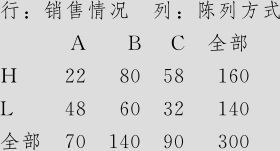
再进行卡方检验（如图6—5下图右半部所示操作）后，可得下列结果：

列表统计量：销售情况，陈列方式

使用销售量中的频率

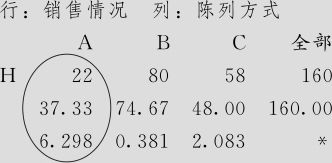
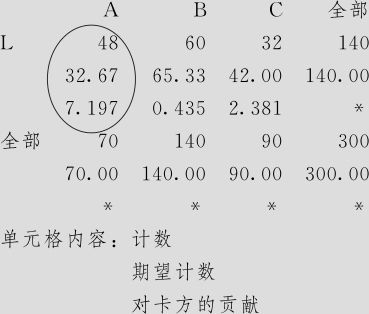
Pearson卡方＝18.776，DF＝2，P值＝0.000

似然比卡方＝19.044，DF＝2，P值＝0.000

这里p值＝0.000＜0.05，得到同样的结论：拒绝原假设，即在α＝0.05水平上，销售情况与陈列方式不具有独立性，商品陈列方式会影响销售情况。

在得到这个显著性结论后，我们可以继续讨论“商品陈列方式如何影响销售情况”的问题。上面得到的总卡方统计量是18.8，它是由6个格的卡方贡献量求和而得到。从6个格的卡方贡献量上看最大者是在“A种陈列方式销售额低”这格中出现的，约7.2，本格中预期出现32.7家门市部，但实际观测值有48家，这说明，A种陈列方式下，销售额低的门市部数比预期的要多；同样分析方式可以得知卡方贡献量次大者（6.3），仍是A种陈列方式，销售额高的门市部数（实际有22家）比预期的37家要少。总之，A种陈列方式导致了销售额降低。同样分析方式可以得知：C种陈列方式导致了销售额增高；B种陈列方式几乎与平均状况无差别。

例6—5

给外商办营业执照，有关部门规定，若在10个工作日内完成任务算“及时”，否则算“不及时”。现将A，B，C三个城市完成任务情况统计如下，见表6—7（数据文件：TBL_及时率.MTW）。

表6—7

问：在α＝0.05水平上，三个城市间完成任务的“及时率”是否有显著不同？

解　应用MINITAB软件进行计算：打开数据文件“TBL_及时率.MTW”，可以从“统计＞表格＞卡方检验（工作表中的双向表）（Stat＞Tables＞Chi-Square test（Table in worksheet））”入口，将工作表中各列（C2～C3）作为响应变量输入，如图6—6所示。

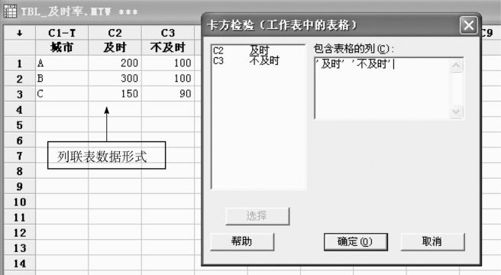
图6—6　多总体比率卡方检验操作图

可得下列结果：

卡方检验：及时，不及时

在实测计数下方给出的是期望计数

在期望计数下方给出的是卡方贡献

卡方＝12.259，DF＝2，P值＝0.002

结论：这里p值＝0.002＜0.05，三个城市间“及时率”有显著不同。从卡方贡献量上最大者入手分析可以看出：城市B不及时者明显偏少，城市C不及时者明显偏多；城市B及时者明显偏多，城市C及时者明显偏少。总之，说明城市B办事效率高，城市C办事效率低，城市A及时率与平均水平没有很大差异。

从本例可以看出，多比率的检验不过是列联表的一个小小应用（列联表含有多行但只有两列）而已。下面我们再举一个处理原始记录的实际应用例题。

例6—6

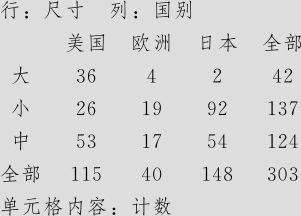
汽车销售商记录了销售的303辆汽车的各项状况，包括：性别、婚姻状况、年龄、购车者国别、汽车尺寸、汽车车型。一部分数据列在表6—8中（数据文件：TBL_汽车销售.MTW）。

表6—8　汽车销售记录表

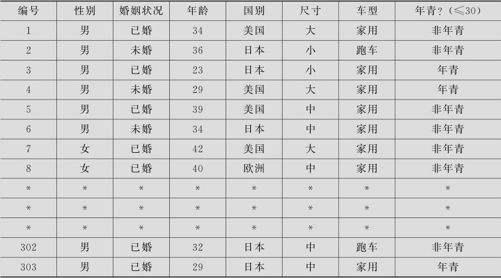
试分析销售“车型”与购买者性别有关吗？与购买者婚姻状况、年龄、国别有关吗？

解　对于这样的原始数据可以用交叉分组表及卡方分析的方法解决。先讨论销售“车型”与购买者性别是否有关问题。

先进行图6—5左半部的操作，将“车型”作为行，将“性别”作为列，得到下列表格：

列表统计量：车型，性别

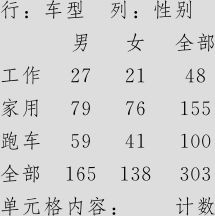
这就是“车型”与“性别”这两个因子间的列联表。

然后再进行卡方检验，得到的结果是：

列表统计量：车型，性别

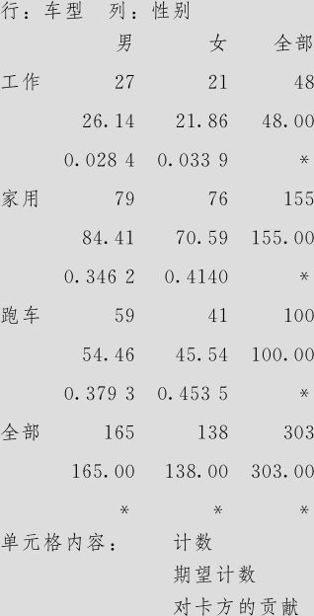
Pearson卡方＝1.655，DF＝2，P值＝0.437

似然比卡方＝1.659，DF＝2，P值＝0.436

由于p值＝0.437，因此销售“车型”与购买者性别无关。

下面分析销售“车型”与购买者婚姻状况是否有关。

将“车型”作为行，将“婚姻状况”作为列，得到下面的列联表：

列表统计量：车型，婚姻状况

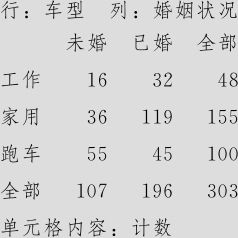
然后再进行卡方检验，得到的结果是：

列表统计量：车型，婚姻状况

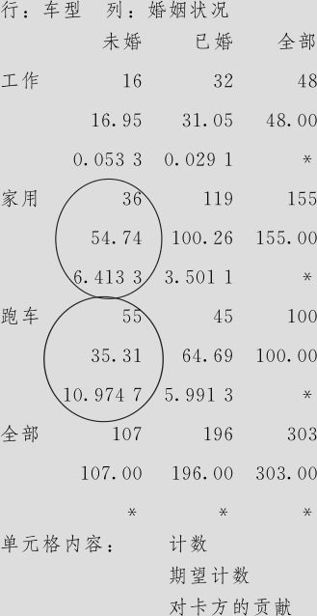
Pearson卡方＝26.963，DF＝2，P值＝0.000

似然比卡方＝26.766，DF＝2，P值＝0.000

首先看到，由于p值＝0.000，因此销售“车型”与婚姻状况有关。这时可以进一步分析“如何有关”的具体状况。由于卡方统计量总共26.963，其中贡献最大者为“未婚而买跑车”的这一格，卡方高达10.97，预期“未婚而买跑车”应该是35.31辆，但实际买了55辆，说明未婚者买跑车比预期的要多。卡方贡献中次大者为“未婚而买家用车”的这一格，卡方达6.41，预期“未婚而买家用车”应该是54.74辆，但实际只买了36辆，说明未婚者买家用车比预期的要少。

其余的分析是类似的。凡是结论为“无法拒绝两因子无关的原假设”时，分析到此为止；凡是结论为“拒绝两因子无关的原假设”时，则要进一步分析两因子间是如何有关的。

下面分析销售“车型”与“年青否”是否有关。

这里要注意，对于“年龄”，我们有详细的记录资料，但我们只能用将年龄分了类的离散型数据：“年青？（≤30）”。把“车型”作为行，把“年青？（≤30）”作为列，得到下面的列联表：

列表统计量：车型，年青？（≤30）

列表统计量：车型，国别

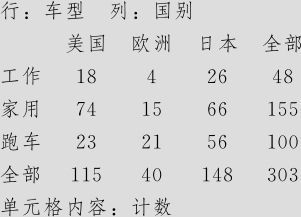
以上都可以得到显著性结论（细节略）。

用完全相同的步骤，可以分析汽车“尺寸”与其他各因子间的关系。结果发现只有“尺寸”与“国别”这两个因子间是相关的。其列联表数据如下：

列表统计量：尺寸，国别

“尺寸”与其他各因子间都是无关的，详细过程不在此赘述。

我们之所以在这里举这个例题，目的在于提醒大家：在日常工作中，像表6—8这样的原始记录到处可见，作为六西格玛管理的实践者，千万不要轻易放过这样的原始记录表，只要我们运用统计工具，就一定会从中挖掘出很多有用的信息，而列联表的卡方统计检验就是这种分析中的最有力工具，我们要从实践中很好地学习和掌握它。

到目前为止，我们只讨论了两个属性变量（也称为二维）的列联表问题，但在实际工作中，我们很可能遇到需要同时考虑更多属性变量的情况。其实例6—6汽车销售问题就是一个多属性变量的例子，只不过我们选择其中两个属性变量来讨论罢了。同时考虑多个属性变量需要使用高维列联表，在一般的统计软件中只处理三维列联表分析，更高维的列联表就要使用多元统计中的对应分析工具来解决。牵涉三维列联表时，我们不但要注意到其计算的复杂性，更重要的是高维列联表分析的结论常常会推翻低维列联表所得到的不正确结论，这就是所谓Simpson悖论。下面举例说明。

例6—7

加工生产螺栓的不合格率问题。A，B两个车间都生产同样规格的螺栓，其生产不合格品数的统计结果如表6—9所示（数据文件：TBL_Simpson悖论.MTW）。

表6—9　螺栓生产结果数据表

解　这是双比率检验问题。设两车间的不合格率为P_A及P_B，我们需要检验的是

H₀：P_A＝P_BH_A：P_A≠P_B

用MINITAB软件计算，从“基本统计量＞双比率（STAT＞Basic Statistics＞2 Proportion）”入口，输入相关数据后，得到下列结果：

结果：Simpson悖论.MTW

双比率检验和置信区间

差值估计值：0.0101750

差值的95％置信区间：（0.00563469，0.0147153）

差值＝0（与≠0）的检验：Z＝4.39　P值＝0.000

Fisher精确检验：P值＝0.000

此结果显示，两个车间的不合格率有显著差别，从差值的95％置信区间（0.00563469，0.0147153）可以看出差值肯定为正，即P_A＝0.084249显著大于P_B＝0.074074，即车间B不合格率较低。

此问题也可以用列联表来解决。希望检验“车间”与“合格否”是否相互独立，将表6—9中的“总不合格数”和“总合格数”这两列填写入列联表“包含表格的列”（计算过程与例6—5完全相同，操作见图6—6），得到结果如下：

卡方检验：总不合格数，总合格数

在实测计数下方给出的是期望计数

在期望计数下方给出的是卡方贡献

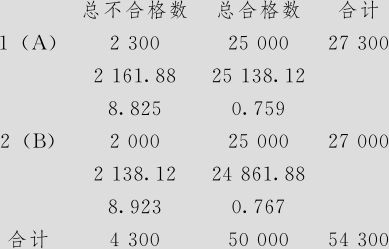
卡方＝19.273，DF＝1，P值＝0.000

由于卡方检验的p值为0.000，可以看出“车间”与“合格否”间肯定是不独立的，也就是说两车间的不合格率有显著差异。这个结论与双比率检验是一致的。从卡方检验结果中可以看出在卡方贡献最大处（卡方为8.923），B车间实际不合格数（2000）远比期望的不合格数（2138.12）少，可以断言B车间的不合格率更低些。

根据上面得到的统计分析结果，我们是否可以得出结论说A车间的不合格率更高些，A车间的生产比B车间的生产更差些？如果收集到的数据到此为止，当然我们就只能得出这样的结论。如果仔细分析生产状况，把“零件”（螺栓）拆分为更细的部件（螺钉和螺母），记录更详细的数据，列在表6—10中（数据文件：TBL_Simpson悖论.MTW，详细数据存在C6～C11）。如何比较两个车间生产的优劣？

表6—10　螺栓生产结果数据详细表

不用统计分析，直接从上表列出的不合格率就能看出，就螺母而言，车间A的不合格率（0.090909）比车间B的不合格率（0.107143）要低；就螺钉而言，车间A的不合格率（0.056604）也比车间B的不合格率（0.065421）要低。这个结论是让人们足够吃惊的，因为此处认为不论螺钉或螺母，车间A都比车间B要好，可是螺钉或螺母合并为螺栓后，我们得到的结论恰好相反：车间A比车间B要差。那么两个结论哪个正确呢？

表6—10中比较并未经过统计分析，我们要把统计分析补充完整才能得出令人信服的结论。

为了使用MINITAB软件，我们要把表6—10的格式稍作更改，形成含“产品”、“车间”、“合格否”3个因子的原始数据型的数据列（见图6—7左图上端。在表6—10中，合格与不合格在不同的列中）。

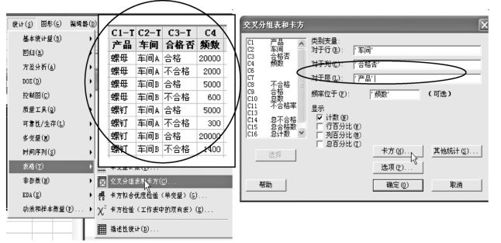
图6—7　卡方检验操作图（三维原始数据格式）

仔细分析一下，立即可以看到这里比例6—4（见图6—5中上图中的表）要复杂，那里只有两个因子（也称为是“二维”的），而现在增多到三个因子（即是“三维”的）。因此操作上也要复杂些，除了“行”、“列”，我们还要增加“层”的内容。操作图与图6—5相同，只是在“交叉分组表和卡方”窗（见图6—5中左下），增加“对于层”，具体填写方法见图6—7中右图：

计算结果如下：

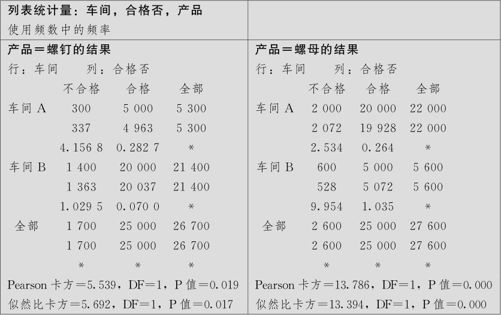
可以看出，这里按层变量（本例是“产品”）取值（本例是螺钉、螺母）分列多个（本例为两个）二维（即普通的）列联表。可以看出，不论是螺钉还是螺母，统计检验结果都是显著的（α＝0.05），而且都是车间A的不合格率要低。

这里自然要产生疑问，怎么会有这样奇怪的结果呢？仔细分析可以知道，由于螺钉比螺母的加工要容易些，生产螺钉的不良率要低于生产螺母的不良率，实际生产过程中，车间A虽然比车间B不良率低些，但车间A大量生产的是较难加工的螺母，而车间B大量生产的是较容易加工的螺钉，不加区分地把螺钉与螺母统称为“零件”，把加工螺钉与螺母的数据不合理地求了和，最后就造成了上述问题。

最早分析这种现象的是美国法律学家辛普森（Simpson），他在研究美国佛罗里达州的犯罪问题时发现，白人杀手被处死刑的比率要高于黑人杀手；但如果把被害人的肤色也考虑进来时，他发现，不论被害者是白人还是黑人，白人杀手被处死刑的比率要低于黑人杀手，这就得出了矛盾的结论，他认为这是个悖论，故此类现象统称为“Simpson悖论”。他的数据是这样的（见表6—11）：

表6—11　Simpson悖论原始数据

从表6—11中可以看出，黑人凶手被判处死刑的比率低于白人凶手。但是如果加上被害人的肤色，则有更详细的数据（见表6—12）。

表6—12　Simpson悖论原始详细数据

从表6—12中可以看出，加入被害人信息后，不论被害人是白人或黑人，白人凶手被处死的比率都低于黑人。形成这种悖论的原因是，当被害人是白人时，凶手被处死的比率要高于被害人是黑人时凶手被处死的比率。由于白人凶手杀害的更多的是白人，因此造成“白人杀手被处死刑的比率要高于黑人杀手”。辛普森所指出的问题是非常重要的一个概念，但他的原始数列并不具有统计意义上的显著性。类似的例子还有很多，本书9.4节例9—8所分析的上海人口死亡率问题也是这样，在研究不同婚姻状况下的死亡率时，如果不管其年龄状况，笼统分析会得出错误结论说“未婚者死亡率远低于已婚且有配偶者”（这与社会学常识不符），但考虑年龄后，不论哪个年龄段都是未婚者死亡率高于已婚且有配偶者（这就与社会学常识相符而合理了）。

我们学习统计学要特别注意这个问题。在例6—7中，如果我们只根据粗略数据可能会得到的结论说A车间的不合格率更高些；但实际上，不论螺钉或螺母，车间A都比车间B不合格率更低些。我们在六西格玛管理统计中曾反复强调，仅凭数据表面现象不能得出有意义的结论，必须经过统计检验才能说明问题。本书前言中举例说明，100个用户中有75户表示满意，表面上的样本的满意度达到75％，但不能说明满意度比70％有提高，因为经过检验发现结论并不成立；经过统计检验，在400个用户中有300户表示满意，表面上的样本的满意度仍然为75％，但就可以断言满意度比70％有提高。这说明统计检验的必要性。例6—7让我们的认识更上了一层新的境界，那就是说，表面上已经过统计检验得到的结论，也不一定是正确的，其数据可能仍然很粗糙；我们一定要根据实际情况收集更多数据，进行更仔细的分析才可能得出真正正确的结论。

6.3.2　有限项离散型分布的拟合优度检验

当总体有两种类别时，将这两种类别分别以“成功”和“失败”来表示，关于“成功”的比率p的检验在前面章节已经详细介绍了。本节是针对总体中有k种（k＞2）类别时，各类别所占比率结构的检验。

检验的步骤为：

（1）建立假设。我们要检验一个多项分布总体中各类别比率结构是否为规定的p₁₀，p₂₀，…，p_k0时，要求

p₁₀＋p₂₀＋…＋p_k0＝1

所以，我们建立的假设为：

H₀：p₁＝p₁₀，p₂＝p₂₀，…，p_k＝p_k0

H₁：至少一项p_i≠p_i0

（2）抽取样本并进行归类，如表6—13所示。

表6—13　单个多项分布总体抽样类别频数表

其中，O_i（i＝1，2，…，k）表示第i类别的观测频数值，所以n＝O₁＋O₂＋…＋O_k。

（3）确定检验统计量。O₁，O₂，…，O_k是由k个观测值所组成的多元随机变量，它服从多项分布，从多项分布的统计性质可知：n次抽样中第i类别的期望值E_i＝n×p_i0（i＝1，2，…，k）。当O_i实际观测值与期望值相差不大时，可以认为H₀成立；如果相差太大，就认为H₀不成立。按照这样的想法，我们选用统计量：

式中，k代表类别数。

（4）显著性水平为α时的拒绝域为：

例6—8

在五选一的500道考题中，答案是A，B，C，D，E的分别为80，90，125，110，95（数据文件：TBL_试题答案.MTW）。试判断，可以认为选择5种答案的可能性是相同的吗？

解　这是一个离散的均匀分布的假设检验问题。要检验的假设是：

H₀：p₁＝p₂＝…＝p₅＝1/5

H₁：至少有一个p_i≠1/5，i＝1，…，5

应用MINITAB软件进行计算：打开数据文件“TBL_试题答案.MTW”，可以从“统计＞表格＞卡方拟合优度检验（单变量）（Stat＞Tables＞Chi-Square Goodness-of-Fit Test（One Variable））”入口，如图6—8所示输入相关变量。

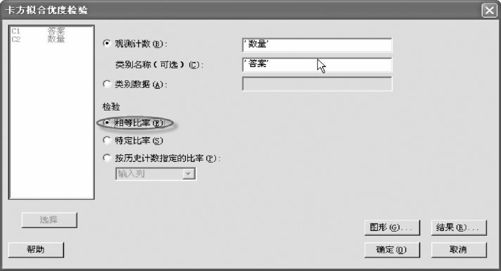
图6—8　多项分布卡方拟合优度检验操作图

可得下列结果：

单变量观测计数的卡方拟合优度检验：数量

在答案中使用类别名称

由于p值为0.014＜0.05，因此可以断言5种答案的可能性并不相同。从进一步的分析中可以看出，上述表中，卡方贡献量最大者是答案“C”（卡方贡献达6.25），期望应该有100题选“C”，但实际上有125题答案为“C”，答案为“C”的题目太多了。

例6—9

现随机抽取500位数码相机购买者，其中各品牌数码相机使用人数如表6—14所示：

表6—14

数据文件为“TBL_市场占有率.MTW”。已知：去年此地区数码相机品牌A，B，C市场占有率结构为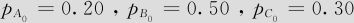：。问在显著性水平α＝0.05下，今年市场占有率结构是否已经发生了变化？

解　（1）建立假设：

H₀：p_A＝0.20，p_B＝0.50，p_C＝0.30

H₁：H₀中等式不全成立

（2）计算各品牌的期望频数E_i和χ²统计量，如表6—15所示。

表6—15　期望频数E_i和χ²统计量计算

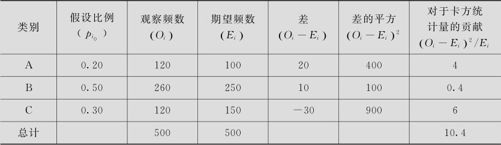
由于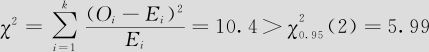，统计量落在拒绝域中，拒绝原假设，即在α＝0.05水平上，认为该地区数码相机品牌A，B，C市场占有率结构已经发生变化，不再是p_A＝0.20，p_B＝0.50，p_C＝0.30。

用MINITAB软件计算：打开数据文件“TBL_市场占有率.MTW”，从“统计＞表格＞卡方拟合优度检验（单变量）（Stat＞Tables＞Chi-Square Goodness-of-Fit Test（One Variable））”入口，如图6—9所示输入相关变量。

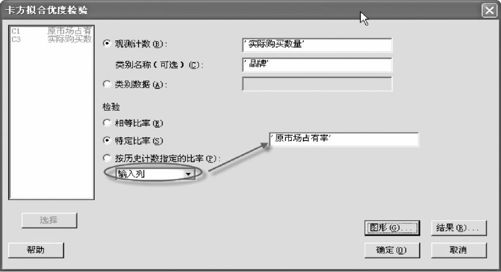
图6—9　卡方拟合优度检验操作图

点击“确定”后，可得下列结果：

单变量观测计数的卡方拟合优度检验：实际购买数量

在品牌中使用类别名称

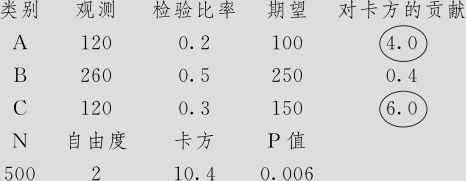
这里p值＝0.006＜0.05，得到同样的结论：拒绝原假设，所以在α＝0.05水平上，认为该地区数码相机厂商A，B，C市场占有率结构已经发生变化，不再是p_A＝0.20，p_B＝0.50，p_C＝0.30。这里，卡方贡献最大者为品牌C（卡方达6.0），原因是按去年比率，品牌C应销售150台，而实际上品牌C只销售了120台，品牌C的占有率比去年下降了；同样，卡方贡献次大者为品牌A（卡方达4.0），按去年比率品牌A应销售100台，而实际上品牌A销售达到120台，品牌A的占有率比去年提高了；品牌B的销售状况几乎与去年相同。

6.3.3　分布的拟合优度检验

各种统计理论或方法均有其基本假设，所以在运用统计工具前，通常需要先检验它的基本条件是否成立。例如，在许多统计工具运用中，常有总体服从正态分布、Poisson分布之类的假设前提，对于总体是否服从特定分布的检验方法称为拟合优度检验（goodness-of-fit test）。对于Poisson分布的检验，自MINITABR15开始，已有专门的窗口，根据总体参数是否已知，结论会略有差异，因此我们分参数已知和参数未知两部分加以介绍。

6.3.3.1　Poisson分布的拟合优度检验

例6—10

每天检查10000支二极管，随机抽取了100天记录的每天二极管不合格数据，对其结果按出现不合格二极管的天数加以整理，如表6—16所示。

表6—16　二极管不合格数数据表

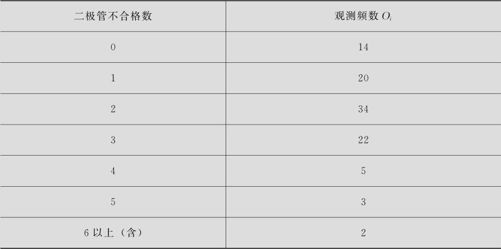
在显著性水平为α＝0.05下，此数据可以认为是服从Poisson分布吗？（数据文件：BS_泊松拟合优度检验.MTW）

解　由于在MINITAB中，已有Poisson分布的拟合优度检验的专门窗口，下面直接使用它。

打开数据文件“BS_泊松拟合优度检验.MTW”，从“统计＞基本统计量＞Poisson分布的拟合优度检验（Stat＞Basic Statistics＞Goodness-of-Fit Test for Poisson）”进入有关界面，如图6—10所示输入相关变量。

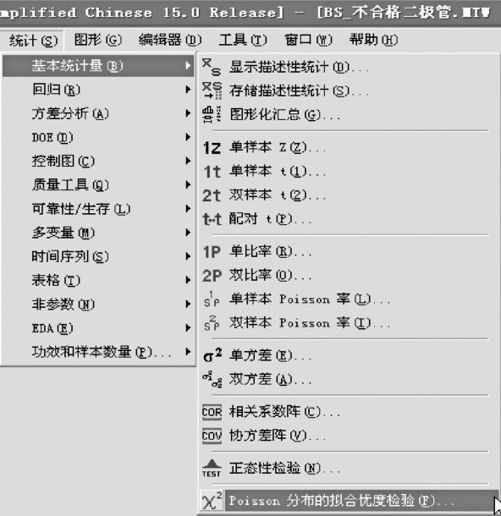
图6—10　Poisson分布的拟合优度检验操作图

点击“确定”后，可得图6—11及下列结果：

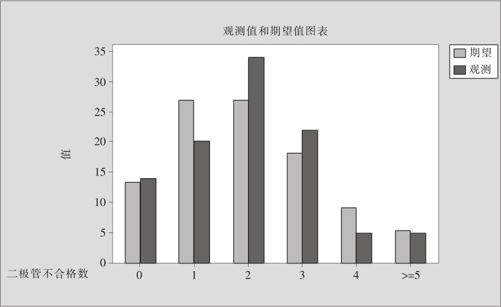
图6—11　Poisson分布的拟合优度检验结果图

Poisson分布的拟合优度检验

数据列：二极管不合格数

频率列：观测频数

二极管不合格数的Poisson均值等于2.01

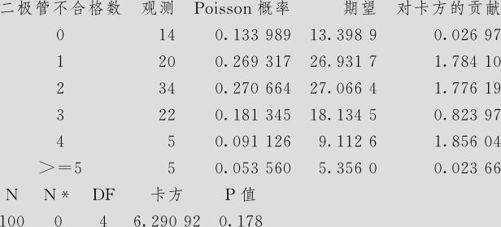
这里p值＝0.178＞0.05，二极管不合格数据可以认为是服从Poisson分布的。

6.3.3.2　参数已知的离散型分布拟合优度检验

虽然在MINITAB中可以简单地使用专门窗口来对Poisson分布进行拟合优度检验，但为了演示一般离散型分布拟合优度检验的步骤，我们将例6—10仔细用手工方法计算一遍，一方面是为了熟悉拟合优度检验方法，另一方面也可以与计算机直接计算的结果相比较。这里的方法几乎和有限项离散型分布拟合优度检验完全相同，只是项数要根据数据类别情况相应设置。

将例6—10的数据重新表述为例6—11加以说明，但这里补充了Poisson率值。

例6—11（续例6—10）

每天检查10000支二极管，随机记录了100天内二极管不合格数数据，其结果见表6—16，在显著性水平为α＝0.05下，问：可以认为此数据记录是服从每天平均不合格数λ＝2的Poisson分布吗？（数据文件：TBL_二极管不合格数.MTW）

解　（1）以X表示每天发生的二极管不合格数，则我们建立的假设为：

H₀：X～Poisson（2）

H₁：X不服从Poisson（2）

（2）若H₀为真时，由Poisson分布概率计算公式：

计算表6—16中二极管不合格数各自出现的概率值，列入表6—17中：

表6—17　各二极管不合格数的概率及期望值

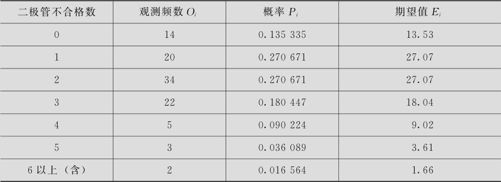
需要注意的是，在整个卡方检验中，各类别的期望值不允许小于5，若某类别出现这样的问题，解决办法是：

（1）将该类别归并到相邻其他类别中；

（2）增加抽样样本数，直到期望值大于等于5为止。

由于表6—17中有两组（X＝5及X≥6）的期望值均小于5，因此将这两组合并为一组后，重新计算得到表6—18。

表6—18　修正后各二极管不合格数的概率及期望值

（3）由于，统计量未落在拒绝域中，不能拒绝原假设，即在α＝0.05水平上，认为此数据记录服从λ＝2的Poisson分布。

用MINITAB软件计算：

打开数据文件“TBL_二极管不合格数.MTW”，从“统计＞表格＞卡方拟合优度检验（单变量）（Stat＞Tables＞Chi-Square Goodness-of-Fit Test（One Variable））”入口，这里我们有以下三种录入数据的方式，如图6—12至图6—14所示。

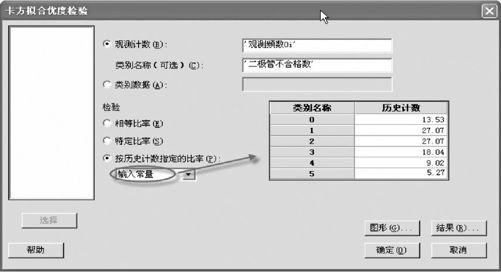
图6—12　分布拟合优度检验理论分布录入方式1

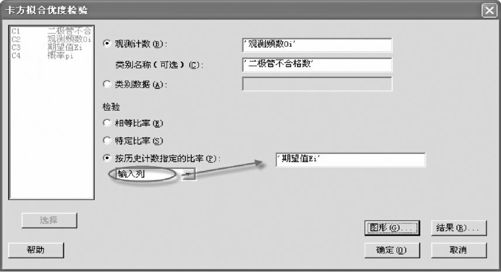
图6—13　分布拟合优度检验理论分布录入方式2

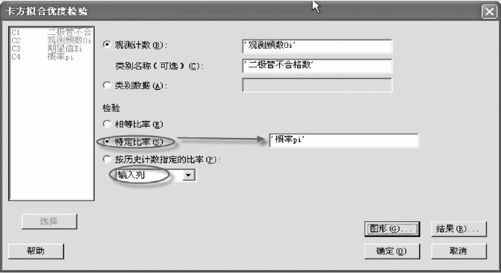
图6—14　分布拟合优度检验理论分布录入方式3

点击“确定”后，可得下列结果：

单变量观测计数的卡方拟合优度检验：观测频数O_i

在二极管不合格数中使用类别名称

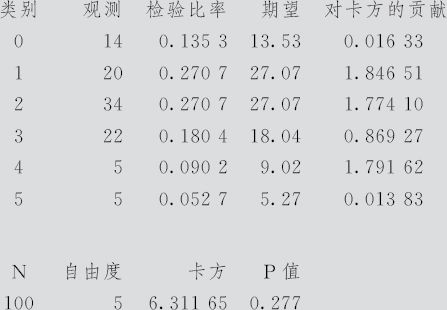
这里p值＝0.277＞0.05，不能拒绝原假设，即在α＝0.05水平上，可以认为此数据记录服从λ＝2的Poisson分布。

注意：这里的计算结果与例6—10的结果有微小差别，原因是数据分7组（大于等于6的单列一组）还是分6组（大于等于5的合并在同一组），其均值的计算结果有差异（分7组时，均值为2.01；分6组时，均值为1.99）。

6.3.3.3　参数未知的离散型分布拟合优度检验

参数未知的拟合优度检验与参数已知的拟合优度检验相比，唯一的差别在于检验过程中需要先进行参数估计，因而造成检验统计量自由度的损失，其自由度损失数量与需要估计的参数个数相等。通常是假定总体所服从的分布类型后，用样本数据估计相应的r个参数，卡方的自由度也会由式（6—13）中的k－1变成k－r－1：

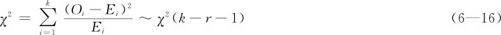
显著性水平为α时的拒绝域也相应变为：

例6—12（续例6—10）

此数据可以认为是服从Poisson分布吗？这里并未指定Poisson分布的均值λ。

解　在例6—10中，已经使用MINITAB软件直接回答了本问题，现在演示一下一般的离散型分布的拟合优度检验方法，同时也可以更深入地理解Poisson分布的拟合优度检验是如何进行的。

（1）以λ表示Poisson分布的均值，则我们建立的假设为：

H₀：X～Poisson（λ）

H₁：X不服从Poisson分布

（2）检验过程跟前例完全相同，只不过在假定Poisson分布后需要先估计出λ的值。

若H₀为真时，计算出表6—19中二极管不合格数的概率值及期望值。如由

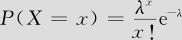
得

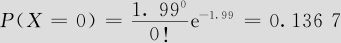
表6—19　修正后各二极管不合格数的概率及期望值

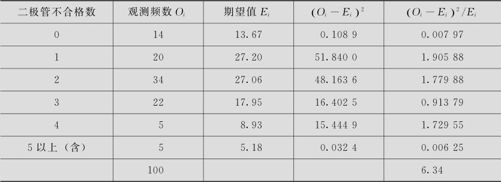
（3）由于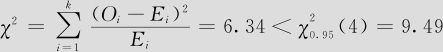，统计量未落在拒绝域中，不能拒绝原假设，即在α＝0.05水平上，认为此数据记录服从Poisson分布。

用MINITAB软件计算：

打开数据文件“TBL_二极管不合格数.MTW”，在这里，直接从“统计＞基本统计量＞Poisson分布的拟合优度检验（Stat＞Basic Statistics＞Goodness-of-Fit Testfor Poisson）”入口，输入数据，点击“确定”后，可得下列结果：

Poisson分布的拟合优度检验

数据列：二极管不合格数

频率列：观测频数O_i

二极管不合格数的Poisson均值等于1.99

这里p值＝0.175＞0.05，得到同样的结论：不能拒绝原假设，即在α＝0.05水平上，认为此数据记录服从Poisson分布。

6.3.3.4　连续型分布的拟合检验

在早期统计应用中，对于一般连续型分布的拟合检验也采用卡方拟合检验方法。其主要思路是：将连续分布通过分割区间实现离散化，然后进行离散型分布的拟合检验。这种方法可以用于任何一种分布，应用非常广泛，但一般来说，精度都不够高，容易犯第二类错误。现在计算机软件发达了，有很多更好的办法可以实现这一目标，下面举例说明。

例6—13

有一组数据，共有30个，其值如表6—20所示（数据文件：BS_连续分布拟合.MTW）。

表6—20

请判断：它服从什么分布？

解　打开数据文件，依次选择“BS_连续分布拟合.MTW”；从“图形＞概率图（Graph＞Probability Plot）”入口（见图6—15）。选中“单一”，则可以进入如图6—16（a）所示界面；再选择“分布（Distribution）”（见图6—16（b）），就可以得到多种分布的选择。假如我们先选择“Gamma”分布试试。

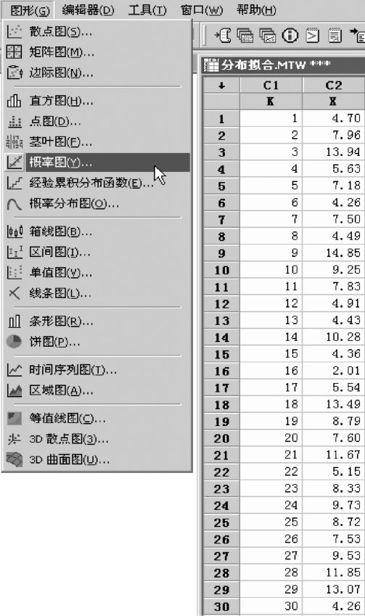
图6—15　连续型随机变量的分布识别操作1

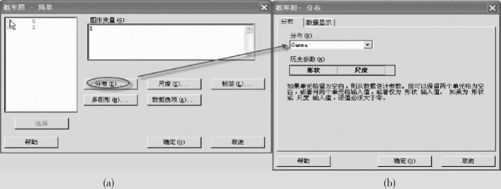
图6—16　连续型随机变量的分布识别操作2

计算机计算后就可以得到图6—17，如果数据在此概率图上基本上呈直线，相应的p值又比0.05大，则不排除是此种分布。由图6—17可以看出，不能排除此数据来自Gamma分布。

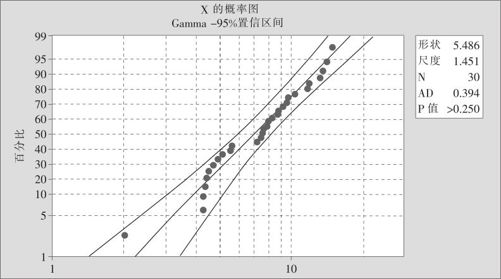
图6—17　连续型随机变量的分布识别结果1

将“分布（Distribution）”换成“Weibul”试验一下，输出概率图如图6—18所示。

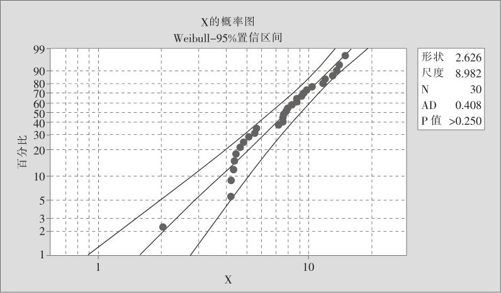
图6—18　连续型随机变量的分布识别结果2

同理，也不能排除此数据来自Weibull分布。

但若换成指数分布（exponential distribution），则数据明显地越出置信范围（见图6—19），另外由于p值＜0.003，可以断言此数据不可能是指数分布。

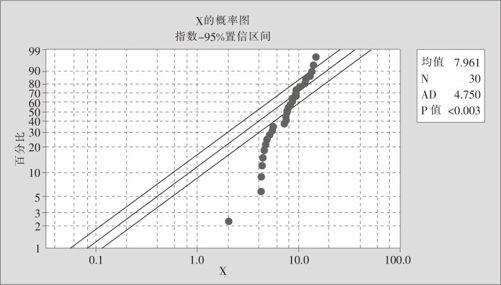
图6—19　连续型随机变量的分布识别结果3

这里所讨论的都是完全数据，即所有数据记录的都是准确数据。在研究可靠性理论时，数据常常是删失（censoring）的，这时如果希望识别分布类型，就要使用可靠性统计理论来处理，这要比完全数据复杂多了。这部分内容请参看本书的姐妹篇《基于MINI-TAB的现代实用统计》，在此就不涉及了。