8.4　用中位数平滑法分析双向表

在实际工作中，常常需要讨论响应变量与两个自变量因子间的关系问题。有时可以认为这里是简单的两因子效应叠加模型，有时则必须考虑两因子间的交互作用。传统的统计分析方法是：假定在所有的处理下获得的数据都服从等方差的正态分布，我们可以使用双因子方差分析方法，分析出各因子的主效应及它们的交互效应，并进一步确认交互作用是否显著。如果交互作用不显著，则可以使用简单的效应叠加模型（additional model）。现在的问题是，如果数据中有相当多的离群值，如何使用可加模型来分析有关结果。传统的方差分析方法要求出各种条件下的平均值，以确定“行效应”、“列效应”以及“交互效应”等，而这样的分析方法不具有耐抗性，在数据中存在离群值的情况下就不能再使用了。EDA提供的“中位数平滑法”（median polish）正是用来解决此问题的。

8.4.1　中位数平滑法的原理及方法概述

先看一个实际例子，从这个例题可以看出双向表的概念及用途。

例8—3

研究三种头盔的抗冲击性能。头盔的类型（因子A）有三种，在这三种头盔中，力的作用位置（因子B）有两种：作用于头盔的前部或后部。在同等大小的撞击力下，能够削减的撞击力是响应变量，对每种头盔的两个位置各测量了2次（削减的）撞击力。希望确定这里是否存在任何可识别的数据模式，同时要指明三种头盔类型之间的差异和作用点（头盔前部与头盔后部）的差异，并综合评价头盔所能提供的保护水平（由“撞击力”度量）。这里考虑了两个因子（头盔类型A和撞击力的作用位置B），而且对这两个因子的每个搭配都进行了2次重复试验。希望分析因子的主效应是否显著，二因子的交互效应是否显著。数据列在表8—5中（数据文件：EDA_中位数平滑.MTW）。

表8—5　头盔撞击力试验数据表

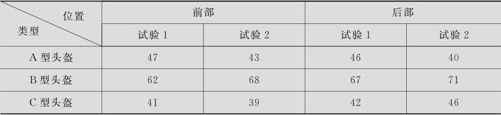
传统的二因子方差分析方法似乎可以解决此问题。但使用方差分析方法的关键，是在对效应进行评价时，使用的是各种条件下的平均值，而平均值不具有耐抗性，因而导致分析方法整体上就不具有耐抗性。EDA方法中关键的一步就是将“平均值”改为“中位数”。

在EDA中，数据的存放格式与方差分析类似，仍称之为“双向表”（two-way table）。记因子A有k个水平，因子B有m个水平，在A_i与B_j的每个搭配条件下，得到观测值：

把简单的可加模型写为：

式中

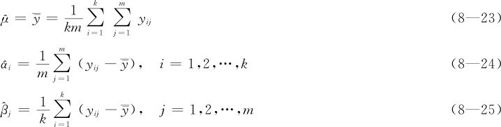
这时，我们可以定义响应变量的残差平方和（sum of square of residual，SSR）为：

在ANOVA中，我们拟合这批数据的“最优”可加模型，就是选取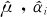及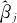使SSR达到最小。按照最小二乘原理，这里取相应的平均值就会达到这一目的，因而就有了完整的方差分析方法。但这一切都要先假定ε_ij是相互独立、等方差、均值为0的正态（高斯）分布。但当这个假定不成立时，最小二乘原理就不再适合。正如同考虑一组数据x_i，如何选择值c，能使

达到极小？回答应该是取其平均值

如果问题换成如何选择值c，能使

达到极小？回答应该是取其中位数

类似地，如果考虑模型

希望讨论如何选择各参数，以使得绝对残差和（sum of absolute-value of residual，SAR）

达到极小？我们猜测上述参数都取各自的中位数将可以实现这一点，这就是“中位数平滑”的基本思路。数学理论上的研究表明，可以举出反例来说明中位数平滑的方法有时确实不能使SAR达到最小（参见本书参考文献［17］），但实践经验表明，上述反例实在是非常罕见的，在一般情况下，中位数平滑的方法是行之有效的。MINITAB软件也是基于此而将这一方法付诸实施。作为实际工作者，理解理论分析中的各个细节并不重要，理解这些方法的含义才是最重要的。我们之所以要学习EDA方法，主要是担心数据中有异常观测值出现，如何使分析方法具有耐抗性是主要的出发点。中位数平滑法既然是行之有效的，我们学会使用它就够了。

8.4.2　中位数平滑法的实例分析

回到例8—3，我们希望分析出三种头盔类型之间的差异和作用点（前部与后部）的差异，并综合评价头盔所能提供的保护水平（由“撞击力”度量）。也就是希望分析两个因子的主效应是否显著，并使用可加模型分析解释有关结果。

在MINITAB软件操作中，“中位数平滑”本身并不显示任何结果，只能将结果存储下来，并利用显示工具显示出来，然后再加以分析。

从“统计＞EDA＞中位数平滑（Stat＞EDA＞Median Polish）”入口（出现窗口见图8—14），在“响应（Response）”中填写入“撞击力”，在“行因子（Row Factor）”中填写入“头盔型”，在“列因子（Column Factor）”中填写入“位置”，并要求存储公共效应（它是常量，要特别命名，不妨记为A1）、行效应、列效应及比较值，另外要求存储残差与拟合值。

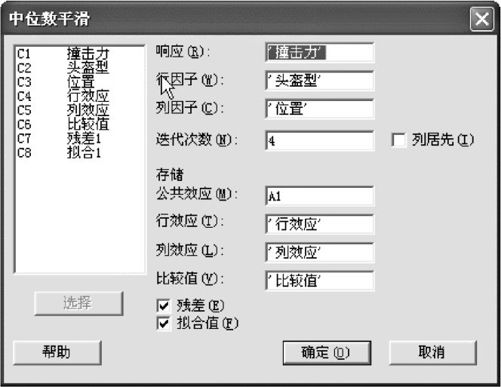
图8—14　头盔撞击力的中位数平滑操作

运行后就得到如图8—15所示的结果（显示在原数据表的后列）。

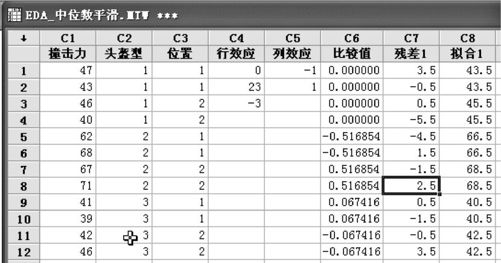
图8—15　头盔撞击力的中位数平滑结果

为了显示其他方面的结果，要使用下列操作：从“数据＞显示数据（Data＞Display Data）”入口（出现窗口如图8—16所示），在“要显示的列、常量和矩阵（Columns，constants，and matrices to display）”中填写入“A1”，则可以在运行窗中看到公共效应A1之值。

图8—16　头盔撞击力的显示公共效应数据操作

从“统计＞表格＞描述性统计（Stat＞Tables＞Descriptive Statistics）”入口（见图8—17），出现界面见图8—18左半部。在“对于行”中填写“头盔型”，在“对于列”中填写“位置”。打开“关联变量”窗口后（出现界面见图8—18中右图），在“关联变量”中，填写“撞击力”、“拟合1”及“残差1”，在“显示”中，选中“数据”。

图8—17　头盔撞击力的中位数平滑结果显示操作1

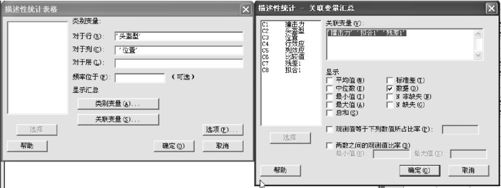
图8—18　头盔撞击力的中位数平滑结果显示操作2

最终可以在运行窗中得到输出结果，整理后可以看出它是如表8—6所示的一个表格。

表8—6　头盔撞击力的中位数平滑结果

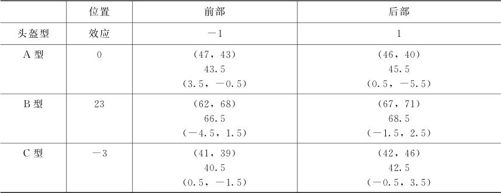
单元格内容：撞击力原始数据（2个）

拟合数据

残差数据（2个）

下面对这些结果加以解释和说明：

从数据分析结果可知，公共效应（它代表“撞击力”的一般水平）为44.5。行效应（头盔类型效应）解释了相对于撞击力公共值在不同行之间发生的变化（即不同头盔类型的变化）。对于头盔类型A，B和C效应分别为0，23，-3，这表明头盔类型B的耐撞击力比公共水平高很多；而头盔类型C的耐撞击力比公共水平略低。列效应解释了相对于撞击力公共值在不同列（即不同撞击位置）之间发生的变化。对于前部和后部，效应分别为-1，1，表明撞击头盔前部略低于头盔耐撞击力公共值，撞击头盔后部略高于头盔耐撞击力公共值。每个单元格的两个观测值的原始值、拟合值及残差值都显示在每个小表格中。

这里还有需要深入探讨的问题。从数据结果上看，A型前部残差和为3，A型后部残差和为-5；B型前部残差和为-3，B型后部残差和为1；似乎头盔类型与撞击位置之间还有交互作用存在（不同的头盔在不同撞击位置上反应不全相同）。至于这里是否真的有交互作用存在，要用到更细致的工具才能分析，这里就不再继续讨论了。

使用本例数据，直接用双因子方差分析也是可以的。所得出的结论与这里是相似的，如果考虑双因子连同交互作用模型，则可得出如下结论：因子A（头盔类型）效应显著，因子B（撞击位置）效应不显著，A与B交互作用效应不显著。如果数据中存在异常值，则可能会更加凸显出中位数平滑法的优越性。