2.2　随机变量的数字特征

如果已经知道了随机变量的分布，那么我们对于随机变量取值的状况就已经有了规律性的了解。但是，概率分布是个函数，要想抓住一个函数的状况是很不容易的。比如公司领导问你：“昨日深市A股状况如何？”你说：“我这里有股市日报，昨日所有几千份A股的价格全在里面列出了。”这样的回答当然不能令人满意。你至少要说“昨日深A指数是12789，比前天上涨了0.38％”，等等。换言之，你总要把一大堆数字归纳成几个特别有代表性的数字，用以代表总的状况。又例如，你在自由市场上买了一堆河虾，你可以说：“这些河虾平均每斤50只，个头虽不大，但还算整齐。”这里就是至少提供了两方面的信息：平均值如何，分散程度如何。从统计学的理论描述上来讲，这就是“平均值”和“方差”两个基本概念。当然，描述平均状况和分散状况的量还不止这两个，以后还会陆续介绍。

2.2.1　随机变量的均值

随机变量最重要的特征就是平均值（mean）。用E（X）来代表随机变量X的数学期望或平均值，有时也可以简化用单一的希腊字母μ来表示。平均值有时也简称为均值。对于离散型或连续型随机变量，E（X）的定义很不相同。下面分别讲述。

2.2.1.1　离散型随机变量的均值

我们先举一个例子说明究竟应该怎样计算平均值。假设一个班，在数学考试中，考试成绩如下（这里为了集中精力思考概念，例子已作了简化）。

例2—2

A班数学期末考试成绩如表2—4所示。求全班数学考试平均值。

表2—4　A班数学期末考试成绩表

显然，我们不能简单地将分数60，70，80，90，100平均起来，得到80。我们一定要考虑得此分数的人数。因此，平均值应该为：

μ＝（60×30＋70×60＋80×80＋90×20＋100×10）/200＝76

如果我们先将分母分别放入括号中的每一项，也就是先计算出每种得分所占的比率，则可以根据算术中的分配律将上述算法换成另一种等价算法：

μ＝60×0.15＋70×0.3＋80×0.4＋90×0.10＋100×0.05＝76

这两种算法结果当然应该相同，但是后一种计算方法有更明确的概率的含义。也就是说，只要将所取的值与取此值的比率相乘再相加，就可以得到平均值。利用与此相似的方法就可以得到随机变量的平均值。比如，离散型随机变量X的分布如表2—5所给定。

表2—5　质量等级的分布律表

例2—3（续例2—1）

质量等级的分布律在表2—5中列出。求平均质量等级。

由于此表中的第一行列出的是随机变量所取的值，第二行列出的是随机变量取此值相对应的概率。因此容易想到，平均质量等级应该是：

μ＝1×0.1＋2×0.2＋3×0.3＋4×0.3＋5×0.1＝3.1

根据上例的启发，我们就可以得到一般的离散型随机变量的平均值的概念。

设一般离散型随机变量X的分布律为表2—6：

表2—6　一般离散型随机变量分布律表

我们用μ表示随机变量的均值，则为：

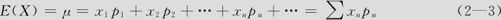
如果随机变量仅取有限个值，则式（2—3）的表达式中的求和只有有限项。如果随机变量取无限个不同的值，则式（2—3）的表达式中可能有无限项，这就成了无限项求和的问题。严格说来，我们当然至少得要求此求和是“收敛”的。如果求和不收敛，则均值就不存在。由于不“收敛”的情况是很罕见的，我们在此不详细讨论，我们总假定均值是存在的。

从物理意义上看，平均值相当于质心的位置。比如，在一根水平横放的细棒上，在位置x₁处，放着比率p₁的质量；在位置x₂处，放着比率p₂的质量；…，如图2—11所示。

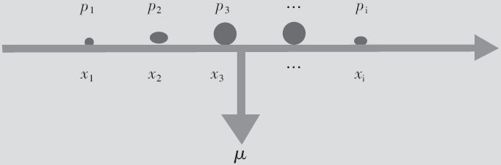
图2—11　离散型随机变量均值示意图

那么，整个系统的质心的位置，就应该是μ所在的位置。

2.2.1.2　连续型随机变量的期望值

对于连续型随机变量的分布，我们可以用分布密度p（x）（或f（x））来表示。如果分布密度的图形已经给定，可以仿照离散型随机变量求质心的思想给出均值的定义。我们设想以分布密度曲线作为上边界，横轴作为下边界，这样形成一块薄板。如何求这块薄板的质心呢？图2—12就是连续型随机变量的均值作为质心的示意图。

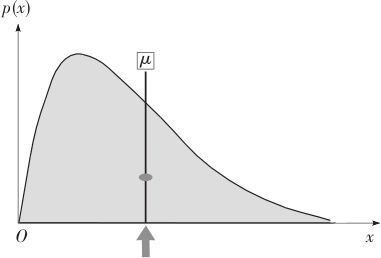
图2—12　连续型随机变量的均值μ示意图

由高等数学的公式可以得知，全部面积应该为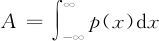：；全部质量矩应该为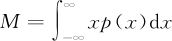：，因此质心的横坐标为：

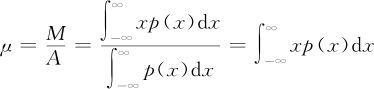
最后一个等式的成立是由于我们总假定分母上的图形总面积为1，因此可以容易理解连续型随机变量的平均值的定义：

换言之，随机变量的均值就是该密度图形质心的横坐标。

很显然，如果分布是对称的，则均值一定正好是分布的对称中心。如果分布非对称，则要针对具体的分布具体计算之。通常说来，计算均值是件不容易的事，可是对于非专业的统计工作者而言，计算均值的过程并不重要，而对于均值概念的深入理解才是最重要的。本章2.3节和2.4节将给出常用的一些分布的均值数值公式供大家参考使用。

这里还要给出计算平均值的一种推广形式。

例2—4

航班每次飞行坠机概率为十万分之一，每位乘客保费为20元，死亡赔付金额为40万元。问保险公司从每位顾客手中平均获取多大利润？

解　记随机变量X为事故发生指示变量：当飞行平安时，X＝0；当飞行出事故时，X＝1。

由所给条件可知，P{X＝1}＝0.00001，P{X＝0}＝0.99999。随机变量X的分布律在表2—7中的前两行给出。

表2—7　保险公司航空保险事故分布律与赔付表

我们要讨论的不是发生事故的可能性问题，而是保费问题。投保时，乘客交一定保费，当未出事故时，乘客保费归保险公司所有，一旦发生事故，则保险公司要按约定好的保险额予以理赔。保险公司有时赚有时赔，那么平均说来，保险公司在每个客户身上的平均获益是多少呢？设Y为保险公司收益，无事故为20元，有事故为（20－400000）元，因此平均收益为：

E（Y）＝20×0.99999＋（20－400000）×0.00001＝16

这里我们用E（Y）代表对于Y求期望（expectation），它的真实含义就是求平均。在本例中，E（Y）＝16，换言之，保险公司在每个客户身上的平均获益是16元。扣除相关费用，它的利润绝对是非常可观的。

一般说来，对于随机变量X的某个函数Y＝g（X），求Y的期望值时，可以对于每个Y的取值按X的取值概率求其平均值。

根据上面这条性质，可以很容易地得到下列常用公式（式中，a，b都是普通常数）：

1．E（aX＋b）＝aE（X）＋b

2．E（aX₁＋bX₂）＝aE（X₁）＋bE（X₂）

这两条性质是普遍成立的，不需要任何关于独立性及分布方面的条件。

2.2.2　随机变量的方差

对于一个随机变量的分析，了解其均值当然是重要的。但仅知道均值是远远不够的。“一个社区内每户平均月收入为3000元”是否说明该社区内收入状况不错了呢？那要看各户收入之间的差别波动大不大。为了度量这种波动，可以有多种计算方法。计算出随机变量的方差（variance）是最重要的一种。我们参看图2—13，了解一下不同分散程度的图形。

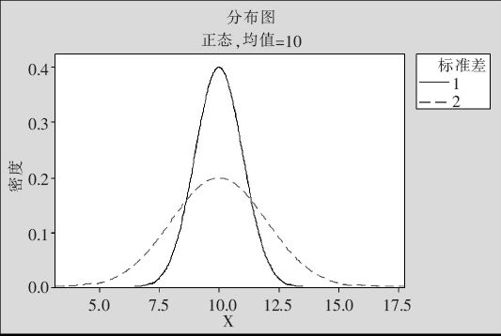
图2—13　两个分布的分散程度比较

这个图中的两个分布中，均值是相同的，都是10。它们的差别是分散程度不同。很明显，图形较“瘦”的表示分散程度较小；图形较“胖”的表示分散程度较大。我们用V（X）或σ²表示随机变量X的方差（也有书籍用记号Var（X）或D（X）表示随机变量X的方差），它的定义是随机变量与其均值之差的平方的平均值。用数学公式来写就是下述公式：

很明显，不论随机变量X的取值比μ大，还是比μ小，由于（X－μ）²的取值都会是正数，X取值偏离μ越远，则（X－μ）²的取值会越大。因此可以看出，如果数据越分散，则V（X）的值会越大。因此，方差代表的量就是随机变量分散的程度。比如，从天然河流中钓来的鱼和从农贸市场上买来的鱼的最主要差别是什么呢？区别不在于鱼的平均长度如何，而是钓来的鱼的长度之方差会远比买来的鱼的长度的方差大得多；解放军仪仗队士兵为了显示雄壮有力，其身高一定要平均值较大，而身高的方差要较小。

方差的物理意义也是很明显的，随机变量的均值是该密度图形质心的横坐标，方差则代表该密度图形绕质心的转动惯量。比如在图2—13中，很明显，较“瘦”的图形绕质心旋转启动或制动旋转都会比较容易，较“胖”的图形绕质心旋转启动或制动旋转都会比较困难。这正是“转动惯量”的含义。方差越大，代表数据越分散；方差越小，代表数据越集中。

但方差有个先天性缺点。大家知道，均值的量纲与原随机变量X的量纲［X］是一致的；而方差的量纲则是X量纲的平方，即为［X］²，这使得理解起来不够直观。为此我们引入标准差（standard deviation）的概念，它常用希腊字母σ（读音为“西格玛”）表示。由此可知：

以上给出的计算随机变量方差公式对于连续型或离散型随机变量都是相同的，但具体求法却不完全相同。对于计算方差公式（2—5），具体化为离散型随机变量时则为：

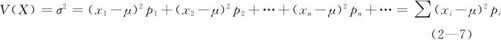
对于计算方差公式（2—5），具体化为连续型随机变量时则为：

例2—5（续例2—1）

质量等级的方差计算。在例2—3中，已经知道平均质量等级为μ＝3.1，因此根据式（2—7）可得

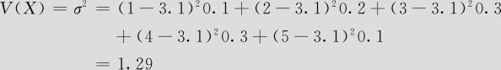
根据式（2—6）可得

σ＝1.1358

对于连续型随机变量，计算方差通常都要用定积分进行。这些计算通常都很复杂，统计工作者早已帮我们计算好，我们不必过问计算过程，只要明白其概念就够。下面我们用正态分布加以解释。

中国成年男子身高（单位：cm）的分布如图2—14所示。

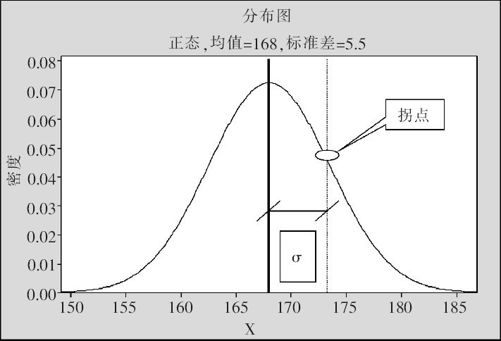
图2—14　中国成年男子身高分布密度曲线及标准差示意图

正态分布的密度曲线是钟形的，最中间是对称中心的均值位置，曲线的两端是下凸的（凹的），中心段部分是上凸的，在凹与凸的交界处有个转折点，称为拐点。拐点到中心线的距离就是标准差σ。很明显，与方差的概念完全一致，标准差越大，代表数据越分散；标准差越小，代表数据越集中。

其他分布的方差的计算比较复杂，我们这里不准备给出。下面的两节介绍常用分布时将给出它们的均值和方差公式。

方差是度量随机变量分散程度的最有力的工具。我们常用到它们的一些性质。从方差的概念，很容易得到下列常用性质（式中，a，b都是普通常数）：

（1）V（C）＝0（任意常数的方差是0）

（2）V（aX）＝a²V（X）（随机变量增大为a倍时，其方差将增大为a²倍）

（3）V（aX＋b）＝a²V（X）

（4）在X₁与X₂相互独立时：

V（X₁＋X₂）＝V（X₁）＋V（X₂）

V（X₁－X₂）＝V（X₁）＋V（X₂）

即两个相互独立的随机变量，其和（或差）的方差是二者方差之和。更一般的公式是：

（5）

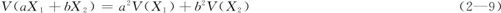
这里我们未加解释就引用了两个随机变量相互独立的概念。对于随机变量独立性概念我们只要考虑到：对于第一个随机变量X的任意取值都不会影响第二个随机变量Y的取值时，则称两个随机变量是相互独立的。上述性质4说明了独立随机变量间方差关系式，这在后面会多次用到。

（6）如果有多个随机变量X₁，X₂，…，X_n，它们相互独立，且各方差都相等（记为σ²），则

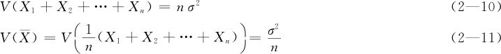
2.2.3　随机变量的偏度与峰度

只用反映位置状况和离散程度的参数来描述随机变量的分布仍然不够完善。如果能增加有反映随机变量分布形状的参数配合前两者，将更能完整地呈现随机变量分布的特性。偏度和峰度是最常用的两个度量数据分布形状的参数。

2.2.3.1　偏度

偏度（skewness）是对随机变量分布不对称性的度量，用β_s表示。其计算公式为：

式中，μ为分布的均值；σ为分布的标准差。

它的含义是：当分布完全对称时，则β_s＝0。正态分布对称，当然它的偏度就为0（见图2—15B）；反之，β_s＝0时，分布并不一定对称，但一般说有某种对称性。当β_s＞0时，分布称为正偏（也称右偏），它的分布中高于均值的“尾”部向右侧延伸严重（见图2—15C），当β_s＜0时，分布称为负偏（也称左偏），它的分布中低于均值的“尾”部向左侧延伸严重（见图2—15A）。负偏分布在实际工作中很少出现，而大多数偏态分布都是正偏的。正偏分布常见于寿命分布、社会状况（收入、住房等）、水文气象（年最高气温、雨量、水位、风速、波高）等领域内的数量分布。

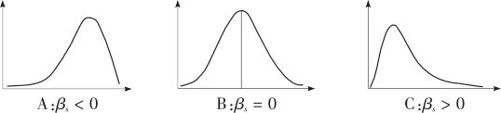
图2—15　偏度示意图

2.2.3.2　峰度

峰度（kurtosis）度量随机变量分布中间部分的陡峭程度及两端尾部的厚重程度，也可以简单地当作分布平坦性的度量，用β_k表示，计算公式为：

式中，μ为分布的均值；σ为分布的标准差。

我们理解峰度含义的时候，一定要注意，比较两个分布的峰度时，一定要让它们二者有相同的均值和相同的方差，否则比较的不是峰度而常常变成比较方差了。可以参考图2—16，各分布都有相同的均值及方差。当数据为正态分布时，其峰度为0。正峰度表示数据分布比正态分布中间顶峰更峭、两尾更重；负峰度表示数据分布中间比正态分布顶峰更平、两尾更轻。负峰度常在均匀分布类型或多个不同均值的混合正态总体中出现。

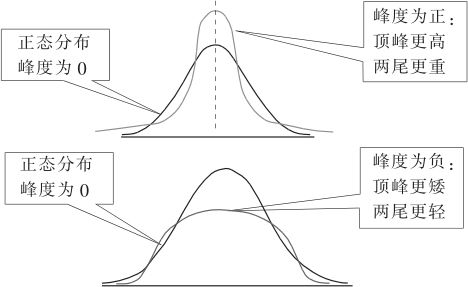
图2—16　峰度示意图

2.2.4　随机变量的累积分布函数及分位数概念

对于随机变量的数字特征，除了常用的均值及方差之外还有很多。为了将来计算这些数字特征，也为了计算随机变量取值的概率，有必要先引入累积分布函数的概念。

2.2.4.1　随机变量的累积分布函数

我们以连续随机变量为例。当分布密度p（x）给定之后，我们可以直观看到随机变量取值的规律，看到哪个部分概率大，哪个部分概率小。但是如果我们真的要求出落入某范围内的概率，则要用定积分求出面积才行。一般说来，求积分是很困难的，有些甚至是不可能的（例如，正态概率密度的积分就得不出普通的初等函数）。为了能顺利计算出落入任意一个区间的概率，我们引入累积分布函数概念，这就使计算概率的工作变得非常简单。

我们用F（x）代表累积分布函数（cumulative distribution function，简记为cdf）或简称为分布函数。对于任意指定的x值，累积分布函数F（x）代表随机变量落入其左方的概率，它的含义如图2—17阴影部分所示。

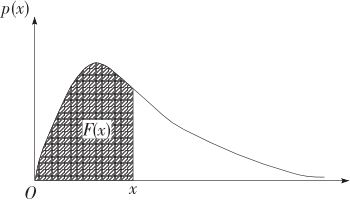
图2—17　累积分布函数示意图

从累积分布函数的定义可以看出下列性质：

（1）当x趋于负无穷时，F（x）趋于0；当x趋于正无穷时，F（x）趋于1。

（2）x逐渐增长时，F（x）也会逐渐增长，至少不会减小。

（3）落入区间［a，b］的概率，可以用公式来计算：

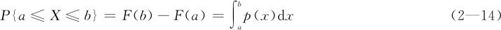
用图形来显示概率，如在图2—18中，图中阴影部分的面积就是随机变量落入此区间的概率。因此，如果已知累积分布函数时，则计算落入［a，b］区间的概率，可以用F（b）与F（a）之差直接求得，即要学会使用式（2—14）的前半段：

P{a≤X≤b}＝F（b）－F（a）

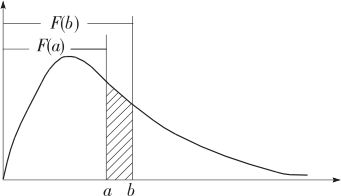
图2—18　随机变量在指定区间内取值的概率计算示意图

其示意图见图2—18。

在上述图形中，容易看出式（2—14）的下面两种特例情况：

1）当a为负无穷时，由于F（a）＝0，P{X≤b}＝F（b）。

2）当b为正无穷时，P{X≥a}＝1－F（a）。

F（a）的计算通常要用计算机来完成。其一般计算方法是：从“计算＞概率分布（Calc＞Probability Distributions）”入口，选中相应的分布后，在其后面列出了三个选择：“概率密度（Probability density）”、“累积概率（Cumulative probability）”及“逆累积概率（Inverse cumulative probability）”，计算累积概率时选择中间一个（也是默认的选择）；输入一个或多个常数x后，即可以得到对应这些x的F（x）。

例2—6

中国成年男子身高均值为168cm，标准差为5.5cm。试计算：

（1）身高小于160cm的概率。

（2）身高大于180cm的概率。

（3）身高介于160cm～180cm的概率。

解　用MINITAB软件，因为本例牵涉到160和180两个数，可以先在空白工作表上取一列，并命名为H（见图2—19）。

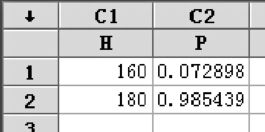
图2—19　概率计算数据输入输出表

从“计算＞概率分布＞正态（Calc＞Probability＞Normal）”入口，选中“累积分布（Cumulative Distribution）”，同时设定“均值（mean）”为168，设定“标准差（Std Dev）”为5.5，同时设定自变量为“输入列（Input Column）”记为H；设定计算结果为“可选存储（Output Column）”记为P，则可以用MINITAB直接计算出概率，并且将结果存在原数据表中的P列内。对于例2—6，从上述窗口进入后可以看到下列对话窗口，当把相应信息填入后，则会得到下列界面（概率的计算结果已列在图2—19内）（见图2—20）：

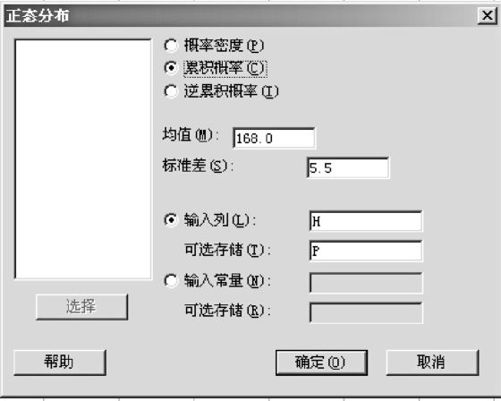
图2—20　概率计算数据操作窗口图

如果只计算单个值的累积概率，可以从“输入常量（Input Constant）”处填写单个x，对于“可选存储（Optional Storage）”通常不选（这时输出结果只在运行窗口中出现）。如果需要将结果存起来，也可以选定一个命名单元。但要注意：单个常数在MINITAB存储中，自己可以选择名称，但由于规定C开头的字母代表一个列，M开头的字母代表一个矩阵，因此要用其他字母例如A1，B3或K18等。对于选定命名单元者，计算机将按指定命名存入内存，以后可以用此命名参加计算。如果想将它显示出来，可以从“数据＞显示数据（Data＞Display Data）”入口，指定名称后，就能将其显示出来。

对例2—6中三个问题的回答结果是：

（1）身高小于160cm的概率。图2—19中第一行已列出。

P{X≤160}＝0.0729

（2）身高高于180cm的概率。

身高小于180cm的概率，图2—19中第二行已列出，因此

P{X≥180}＝1－P{X≤180}＝1－0.9854＝0.0146

（3）身高介于160cm～180cm的概率。

P{160≤X≤180}＝F（180）－F（160）＝0.9854－0.0729＝0.9125

2.2.4.2　随机变量的分位数

在实际工作中，常听说“长江三峡大坝可以抵御长江百年一遇的洪水”。那么“百年一遇”是什么意思呢？有人说：“这很简单，将100年的水位记录下来，最大的水位就是百年一遇水位。”可是这就有个理论上的矛盾，如果有连续两个“百年水位记录”，它们这两组数的最大值不一样（很可能这样），那又该认定哪个值呢？如果有连续十个“百年水位记录”，它们这十组数都各自有自己“百年一遇”值（即各自的最大值），那么又从哪里能得到“千年一遇”值呢？看来这样规定是有毛病的。

如果得到年最高水位X的分布函数，取这样的一个数：随机变量X的取值比它大的概率正好是1/100时，则此数被称为“百年一遇”值。更一般的说法是：随机变量X的取值比它大的概率正好是1/T时，则此数称为“T年一遇”值。

一般来说，对于随机变量X，如果数值x_p可以满足下式：

则称x_p为随机变量X的p分位数。例如：

P{X≤x_0.1}＝0.1

x_0.1就是随机变量X的0.1分位数。按照这样的规定，可以很清楚地得知，“百年一遇”值就是年最高水位分布的0.99分位数，即x_0.99，此数也常称为右侧0.01分位数。同样可以得知，“千年一遇”值就是年最高水位分布的0.999分位数，即x_0.999；“二十年一遇”值就是年最高水位分布的右侧概率恰好为1/20，即0.95分位数x_0.95；“十年一遇”值就是年最高水位分布的右侧概率恰好为1/10，即0.90分位数x_0.9。

求随机变量X的p分位数x_p的工作很重要。其一般计算方法是：从“计算＞概率分布（Calc＞Probability Distributions）”入口，选中相应的分布后，在其后面列出了三个选择：“概率密度（Probability density）”、“累积概率（Cumulative probability）”及“逆累积概率（Inverse cumulative probability）”，计算分位数时选择最后一个：“逆累积概率（Inverse cumulative probability）”，输入常数p，即可以得到随机变量X的p分位数。

对于正态分布及其导出的T分布、F分布、卡方分布等的分位数计算见本书第4章；对于有关寿命分布的分位数计算请参见本书的姐妹篇《基于MINITAB的现代实用统计》中关于可靠性的有关章节。

2.2.4.3　随机变量的中位数

如果p取为0.5，此数特别重要，x_0.5称为中位数，常用m表示。其含义是随机变量X取值中，有一半比m要小，另一半比m要大。画成图（见图2—21），则可以看到，它位于恰好将全部概率分为两半的位置。显然中位数与平均值是两个不同的概念。如果分布图形如图2—21这样，大尾巴在右边，大头在左侧（以后可知这叫“正偏分布”），从重心的概念出发，很容易知道“中位数肯定要比均值小些”。如果分布基本对称，中位数则应该与均值相等。

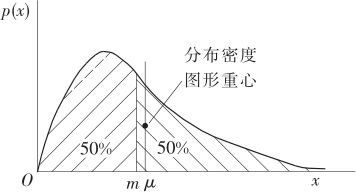
图2—21　连续分布的均值与中位数

为什么一定会有这样的结论呢？初中物理告诉我们物体重心的概念。如果一根电线杆，悬线可以确定其重心的位置（见图2—22），如果用锯沿重心点切开，左右两半的重量相等吗？

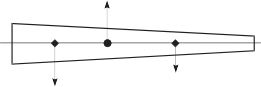
图2—22　非对称物体重心图

观察图2—22，由于右半较细，右半段的重心离总重心一定比左半段的重心离总重心稍远些，而由于左右两段的力矩即“力乘力臂”是相等的，因此可以断定，左侧一定会稍重些。由此可以得知，对于图2—21内的正偏分布的图形，必然可以得到下列结论：中位数m一定在均值μ的左方。

什么情况下用均值作为位置状况的代表，什么情况下用中位数作为位置状况的代表好呢？当然，在分布基本对称的时候，二者相差不大，用哪个都无所谓。但是如果明知分布偏斜很严重，那该如何选择呢？事实上，由于偏斜严重，平均值将会受到尾部数据的强烈影响，因此它的代表性会很差。例如，中国某特大城市，全体有户口的居民平均住房面积达到30平方米／每人，这个结果有代表性吗？按一般规律，住房面积和工资收入等社会指标一样，其分布是严重正偏的。按照“有户口才被统计”的办法，有钱人虽然其人数不算很多，他们的居住面积远远超出大多数人，这些人即使不是该城市长期居民，但他们有“蓝印户口”因而居住面积被统计在内；而非常贫困的住户，像大量的农民工朋友，他们因没有常住户口而根本未统计在内，这样一来，“有户口的居民平均住房面积”就失去了代表性，而“本市所有居民住房面积的中位数”的代表性将会好得多。

2.2.4.4　随机变量的四分位数及四分位数间距

如果p取为0.25或0.75，相当于把整个范围按概率分为相等的四部分，这样的数称为四分位数（quantile），这两个数也很重要：x_0.25称为下四分位数（lower quantile，LQ）或第一四分位数（first quantile，Q1）；x_0.75称为上四分位数（upper quantile，UQ）或第三四分位数（third quantile，Q3）。这两个四分位数连同中位数，都是度量随机变量的位置状况的，它们的含义在图2—23中予以显示。其中LQ与UQ所界定的范围内，将包含约一半的数据，常用来表示数据的主体部分。

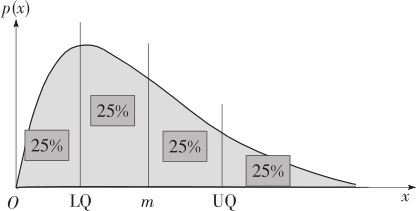
图2—23　四分位数示意图

两个四分位数之间的距离是描述随机变量离散状况的非常重要的参数。它称为四分位间距（inter quantile range，IQR），它的定义就是：

不论分布状况如何不规则或偏斜，IQR总能代表位于中间部位的一半数据的变动范围，因此它的大小可以代表分布的分散程度：IQR越大，则随机变量分布越分散。这个参数对于各种分布（特别是非正态或非对称分布）的应用是很广泛的。