8.1　探索性数据分析的概念

有关EDA的基本概念，我们下面分三小节予以介绍。在8.1.1节中将介绍探索性数据分析的特点；在8.1.2节中将介绍EDA所讨论的四大主题；在8.1.3节中将介绍EDA中常用的术语。

8.1.1　探索性数据分析的特点

探索性数据分析的主要特点有下列三项：

1．一切从原始数据出发

传统的统计方法通常是先假定一个模型，例如数据服从某个分布，特别常见的是正态分布，然后使用适合此模型的方法进行拟合、分析及预测。但实际上，多数试验数据并不能保证满足假定的理论分布。因此，传统方法的统计结果常常表现很差，使用上受到很大的局限。探索性数据分析则完全从原始数据出发，深入探索数据的内在规律性，而不是从某种假定出发，套用理论结论，拘泥于模型的假设。

2．分析方法从实际出发，不强调理论严谨性

传统的统计方法以概率论为基础，使用有严格理论基础的假设检验、置信区间等处理工具。探索性数据分析则以不完全正式的方式处理数据。探索性数据分析方法的选择完全从数据出发，灵活对待，灵活处理，什么方法可以达到目的就使用什么方法。这里要特别强调的是，探索性数据分析更看重的是方法的稳健性、耐抗性，而不刻意追求概率意义上的精确性。

3．分析工具简单直观

传统的统计方法越来越精密，越来越深奥，探索性数据分析则更强调直观及图形化，强调方法的多样性及灵活性，使大多数使用者都能从中分析出有用的信息。

正是由于探索性数据分析的上述特点，因此探索性数据分析提出一些专有术语和名词，它很少照搬传统常用的统计名词术语。这主要出于下列理由：

（1）探索性数据分析（EDA）主要关注的是分析数据全过程的早期阶段，这时还无法进行常规的统计分析。这里所用的技术通常也是与统计学方法不同的，例如茎叶图、字母值、箱线图等，这些工具与术语只在EDA中才会有（箱线图本是EDA特有术语，在统计图形分析中也有相同术语，但含义并不相同）。

（2）EDA的术语与传统的统计术语有关，但不尽相同。例如“四分数”（fourth）（或“折叶数”（hinges））与统计中的“四分位数”（quartile）不完全相同。新术语“批”（batch）就是一组待分析的数据组，它与“样本”（sample）也不全相同，样本通常是要求“相互独立且同分布”的，但“批”并无此要求。

（3）故意回避容易引起误解的术语。例如EDA中常使用“高斯分布”而不用“正态分布”，以免暗示这种分布形状就是通常的形状。

（4）探索性数据分析（EDA）强调的是稳健性概念，因此探索性数据分析的目的与稳健性统计目的是一致的，而与常用统计的目的并不完全相同。

从分析的过程与步骤来看，它也与常用统计方法不同。探索性数据分析的操作步骤大体可以划分为探索及证实两个阶段。

探索阶段主要是判断与分析数据的模式与特点，并将它们有序地展示出来。通常，分析者总是先对数据进行探索分析，然后才能有把握地选择结构变量或随机变量的模型。探索阶段还可以揭示数据对于常见模型的种种偏离。探索阶段的要点是灵活性，既要灵活适应各种数据的不同结构，也要对后续分析步骤所揭示的种种模式灵活反应。

证实阶段主要是评估观察到的模式或效应的再现性。传统的统计分析主要是进行显著性检验或置信区间的估计，证实阶段与此相近，但它还要包含两项内容，一是要把其他密切相关的数据信息结合进来，二是通过收集和分析新数据确认分析结果，为进一步结合模型的统计分析提供线索。

总之，探索阶段强调灵活探求线索和证据，而证实阶段则着重评估现有证据。无论是对大组数据进行分析，还是对相关的几个小组数据进行分析，一般都要经过探索和证实两个阶段，通常还要交替使用探索和证实两种技术，循环反复多次才能得到满意结果。

8.1.2　探索性数据分析的主题

探索性数据分析的全过程有四大主题，即耐抗性、残差、重新表达和启示。

8.1.2.1　耐抗性

探索性数据分析的基本目的是找出所获得的数据的整体性规律，这时就一定要求分析的方法与结论不要受小部分数据的巨大波动的影响，也就是对于数据中的局部不良行为能保持不敏感性，这就是耐抗性（resistance）。对于这种具有耐抗性分析结果的含义是：当数据中的一小部分被新的数据代替时，即使它们与原来的数据很不一样，分析结果也只有轻微的改变。人们之所以关注耐抗性，主要是因为“好”的数据中也难免有百分之几的数据有大错或重大差错，数据的分析要有措施来防御大错产生破坏性影响。从目的上看，探索性数据分析应该不受个别“野值”（wild value）的影响；也正因为如此，在实际确定统计方法时应念念不忘野值存在的可能性，要研究野值存在对于耐抗性的影响，还要研究舍入误差和分组误差对于耐抗性的影响。

耐抗与稳健（robustness）密切相关，但不是一回事。通常认为，稳健性是耐抗性中的一种。稳健性讨论的是统计方法如何能对数据围绕某个特定模型偏离的不敏感性，耐抗性则更广泛些。

8.1.2.2　残差

残差的定义从本书的第9章起将多次引用，但那主要是针对回归分析而给出的，这里的定义比第9章的定义更广泛些：残差（residuals）是数据减去与某模型的拟合值后的差值。这个模型可以是任意一个选定的模型，而不一定限定为回归模型。

EDA认为，分析任何一组数据而不考察残差是不完全的。通过残差分析可以看出数据与模型之间的差距，如果数据组中的大部分都与模型的差距很小，则说明这个模型是个“耐抗拟合”。对于残差有反常的情况时，需要从数据和模型两个方面查找原因：如果残差有系统性行为（如弯曲、非恒定变异等），则修改模型（包括对数据进行变换或选取更细致的模型）将使残差系统性地减小，这时要先修改模型；模型基本上被肯定后，则特别要注意是否有个别点远离模型，分析其产生是否受特殊影响。总之，要兼顾到数据和模型两个方面。

8.1.2.3　重新表达

EDA认为，找到合适的尺度或数据表达方式将大大有利于简化分析，因此要尽早考虑数据的原始尺度是否合适的问题。如果原始尺度不合适，重新表达（re-expression）为另种尺度可能有助于促进出现对称性、恒定变异性、关系线性或效应可加性等。坚持原始测量尺度，对于数据分析并不总是有利的。例如，研究动物肝脏对于某处理的反应，用重量w来反映并不见得比用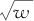或logw更自然，除非已有其他明确的定量知识。重新表达也称为变换（transformations）：对于一组原始数据X，可以使用新值T（X）来代替，这里T（X）是X的某个确定函数。EDA中，最常使用的是Box-Cox变换（即幂变换），也就是说T（X）是X的幂函数。

8.1.2.4　启示

EDA强调图形显示。所谓启示（revelation）就是通过各种图表显示数据分析的结果，直观、简单、一目了然地表述出数据分析的各种情况，显示出其遵循的普遍规律及与众不同的突出特点，促进发现规律，得到启迪，满足分析者的多方面要求。正因为EDA强调图形显示，所以使用了很多新的图解技术，这是EDA对于统计学的主要贡献。

8.1.3　探索性数据分析的术语

前已说明，EDA的术语与传统的统计术语有关，但又不尽相同，学习这些术语时，要注意与传统统计术语的区别与联系。

8.1.3.1　批

“批”（batch）也称为“数据批”，就是一组待分析的数据组。在传统的统计术语中，数据组就是“样本”（sample），但二者也不全相同。样本通常是要求这些数据间“相互独立且同分布”，但“批”则只是原始数据组，并无这些要求。

在传统的统计分析中，常给出一些摘要统计量作为样本数据状况的概括，例如样本均值、标准差等，但这些统计量都不耐抗，对于数据中的野值非常敏感。EDA中则出于探索的目的而选择另类统计量作为摘要统计量，例如选用“中位数”代表位置状况，它就是耐抗的，一批数据中即使一小部分有巨大变化对“中位数”影响也很小。

8.1.3.2　次序统计量

这里的定义与传统的统计分析方法是相同的。对于数据批x₁，x₁，…，x_n，按由小到大的顺序排好：x_（1）≤x_（2）≤…≤x_（n），则x_（1），x_（2），…，x_（3）称为x₁，x₁，…，x_n的次序统计量（order statistics），其中x_（i）称为第i个次序统计量。显然，x_（1）是最小值，x_（n）是最大值。

在排序的基础上，我们继续讨论数据批的结构分析。当顺序是由小到大时，称为是升秩（upward rank），x_（1）称为有升秩1，x_（2）称为有升秩2，…，x_（n）称为有升秩n，一般x_（i）称为有升秩i。当顺序是由大到小时，称为是降秩（downward rank），x_（n）称为有降秩1，x_（n－1）称为有降秩2，…，x_（1）称为有降秩n，一般x_（i）称为有降秩n－i＋1。如果同时考虑升秩和降秩，则对同一个数据，有：升秩＋降秩＝n＋1。升秩和降秩的概念是EDA中独有的，它将导出EDA中最重要的概念之一——“深度”。

8.1.3.3　深度

数据批中一个数据值的深度（depth）是它的升秩及降秩两者中的最小值。在EDA中规定：两个极端值x_（1）及x_（n）的深度为1，x_（2）及x_（n－1）的深度为2，而第i个数据x_（i）及第n－i＋1个数据x_{（n－i＋1）}都有深度i。在EDA中，用深度的概念可以导出一系列探索性的总括值。对于深度，专门规定了记号d，例如d（x_（1））＝1，d（x_（n））＝1，表示的就是x_（1）及x_（n）的深度都为1这样的事实。

8.1.3.4　中位数

在数据批中，将次序统计量求出后，位于最中间的数据称为中位数（median）（这里的定义与常规定义是相同的）。记中位数为M，求中位数运算用med表示，则

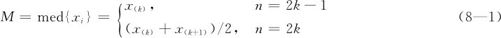
且中位数M的深度应该为：

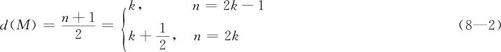
例如，当n＝9时，M＝x_（5），d（M）＝5；当n＝10时，M＝（x_（5）＋x_（6））/2，d（M）＝5.5。

8.1.3.5　四分数

从中位数定义容易看出，中位数将全部次序统计量分为“低值”和“高值”两部分，且这两部分包含的样本数量是相同的。在这两部分数据内部各有一个深度大约为n的四分之一的点，称之为四分数（fourth），用F表示。相应的“低值”和“高值”部分各有一个，分别称为下四分数F_L及上四分数F_U。两个四分数也常被称为“折叶点”（hinges），在MINITAB中常用字母H来表示。四分数F深度d（F）的准确定义是：

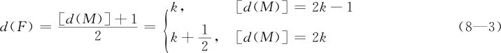
式内的中括号［d（M）］代表对d（M）取整，例如［4］＝4，［4.4］＝4，［4.5］＝4等。如果深度值带0.5，则表示取相邻两个次序统计量的平均值。在式（8—3）中，由于中位数的深度d（M）大约为n的一半，四分数F的深度d（F）大约是d（M）的一半，所以四分数F的深度d（F）大约为n的1/4。

例如，当n＝9时，M＝x_（5），d（M）＝5，则d（F）＝3，即四分数的深度为3，下、上两个四分数分别为F_L＝x_（3），F_U＝x_（7）。

当n＝10时，M＝（x_（5）＋x_（6））/2，d（M）＝5.5，d（F）＝3，下、上两个四分数分别为F_L＝x_（3），F_U＝x_（8）。

当n＝11，M＝x_（6），d（M）＝6，d（F）＝3.5，F_L＝（x_（3）＋x_（4））/2，F_U＝（x_（8）＋x_（9））/2；当n＝12，M＝（x_（6）＋x_（7））/2，d（M）＝6.5，d（F）＝3.5，F_L＝（x_（3）＋x_（4））/2，F_U＝（x_（9）＋x_（10））/2。

我们学习过传统的四分位数（quartile），其中下四分位数（lower quartile）简记为LQ，上四分位数（upper quartile）简记为UQ。在EDA中定义的四分数F与传统的四分位数粗略看起来大体上是一致的，都是将全部次序统计量分成四段，列出位于分界处的值，但仔细比较则可知二者仍然是有区别的。传统四分位数的计算是在正态分布的假定下，求出对于各分位数的次序统计量最佳线性函数的估计公式，而四分数则是在无任何假定条件下，根据深度的概念而给出的公式。下面给出传统的四分位数的具体计算公式，即可看出两者的差别。

例如，当n＝9时，M＝x_（5），LQ＝（x_（2）＋x_（3））/2，UQ＝（x_（7）＋x_（8））/2；

当n＝10时，M＝（x_（5）＋x_（6））/2，LQ＝0.25x_（2）＋0.75x_（3），UQ＝0.75x_（8）＋0.25x_（9）；

当n＝11时，M＝x_（6），LQ＝x_（3），UQ＝x_（9）；

当n＝12时，M＝（x_（6）＋x_（7））/2，LQ＝0.75x_（3）＋0.25x_（4），UQ＝0.25x_（9）＋0.75x_（10）。

与四分数F相仿，可以定义八分数（eighth，记为E）、十六分数（sixteenth，记为D）及卅二分数（thirty-seconds，记为C），每个下层的深度都按式（8—3）由上一层的深度给出。

8.1.3.6　散布

散布（spread）也称为展形或展布，是反映数据离散状况的度量。在EDA中，最常用的散布就是四分散布（fourth-spread），将其用记号d_F表示，其定义为：

它给出数据批内包含中间一半数据的宽度，此量有很强的耐抗性，它几乎不受离群点的影响，而且不受采集的数据量的影响。四分散布与四分位间距（inter quartile range，IQR）相仿，但由于四分数F_L及F_U与四分位数LQ及UQ有差别，四分散布d_F与四分位间距IQR也就有差别了。另外，两个极端值间的散布（即极差）也反映数据的离散状况，但极差受离群值的影响太大，耐抗性太差，只在数据量很少时才使用，通常极差不宜作为数据离散状况的度量。

8.1.3.7　临界值

数据批中常出现一些离群值，但准确判断某个数据是否为离群值并不容易。为此，EDA给出一些作粗略判断用的方法及术语。

称F_L－1.5d_F为下内界值，称F_U＋1.5d_F为上内界值，统称为离群值截断点。

称大于下内界值的最小观测值为下临界值X^L：

称小于上内界值的最大观测值为上临界值X^U：

临界值（criticalvalue）之外仍有数据，则可称之为离群值。可以看出，这里定义的临界值与传统的箱线图“尾端”定义的思路是相同的，只是由于四分数F_L及F_U与四分位数LQ及UQ有差别，四分散布d_F与四分位间距IQR也有差别，因而这里的“临界值”与传统的箱线图“尾端”的准确定义也略有差别。

与此类似，称F_L－3d_F为下外界值，称F_U＋3d_F为上外界值；如果上下外界值之外仍有数据，则可称之为远外值或异常值（outlier）。