13.3　全因子设计

“全因子试验设计”（full factorial design）的定义是：所有因子的所有水平的所有组合都至少要进行一次试验的设计。由于包含了所有的组合，全因子试验所需试验的总次数会较多，但它的优点是可以估计出所有的主效应和所有的各阶交互效应。所以在因子个数不太多，而且确实需要考察较多的交互作用时，常常选用全因子设计。

全因子试验法的思想很简单，用全面搭配的方法来安排试验也是容易实现的，因此全因子设计的计划阶段很容易。我们重点讨论分析阶段。我们强调的是如何使用统计分析工具以获得更多的有用信息。实际上，不使用统计分析工具，即使是用全面搭配的方法来安排试验，在拿到试验结果后，也只是从中挑选那个最优值就结束，因此就浪费了大量的有用信息。试验设计的统计分析方法不但能从试验结果中找到最优值，而且可以判明哪些因子影响显著，哪些因子影响不显著，还可以得到有关的变化规律，预测将要达到的最佳值是多少和这个最佳值将在什么范围内波动。这些就是统计分析方法的威力。

当因子水平超过2时，由于试验次数随因子个数的增长而呈指数速度增长，因而通常只做2水平的全因子试验。如果确实需要做3水平或更多水平全因子试验时，计算机软件中也有与2水平完全相同的试验设计及分析方法，本节对此不再单独叙述。但通常认为，加上了中心点之后的2水平试验设计在工程实践中已经足够，在相当大程度上它可以代替3水平的试验，而且分析简明易行，现已被工程师普遍使用。

13.3.12　水平全因子试验概述

将k个因子的2水平的全因子试验记为：2^k试验。这是整个全因子试验的记号，而不仅仅是试验次数。当然，2^k从数值上看也恰好是k个因子的2水平的全因子试验所需要的最少试验次数。这对理解下节部分因子试验设计的记号是有用的。

1．试验目的

什么时候需要进行2^k试验呢？一般来说，进行任何试验都要进行好几批，大约是：先用部分实施的因子设计进行因子的筛选，让因子个数最后不超过5个，然后用全因子试验设计进行因子效应和交互效应的全面分析。进一步筛选因子直到因子个数不超过3个时，则最后可以用响应曲面方法（RSM）确定回归关系并求出最优设置。因此，部分因子试验通常只是为了筛选因子，可以稍粗糙些，因而试验次数也较少些；而响应曲面试验设计是为了得到包含平方项的非常精细的回归方程，试验次数最多，因而只对较少因子（个数≤3）有实际意义。全因子试验既不像部分因子试验，也不像响应曲面试验设计，它可以兼有筛选因子和建立回归方程（当然只是线性方程）两方面目的。全因子试验可以分析出所有因子主效应和各因子间的所有各阶交互作用的效应，回归方程中将包含全部一次项和各因子的乘积项，试验次数也较适中，可以适用于因子个数不超过5的情况。由于全因子试验设计方法和理论是理解部分实施因子试验方法和响应曲面试验设计方法的基础，因此本节详细介绍全因子试验设计。

2．正交试验设计概念

早在20世纪20年代，著名统计学家费雪在农田试验中已经使用正交试验方法来安排试验，与他同时期的耶茨（F. Yates）及芬尼（D. J. Finney）也都对分区组、随机化、重复试验以及正交性等方面做出了卓越贡献。到了40年代，印度统计学家劳（C. R. Rao）首先提出正交阵列这种更广泛的设计理念，其强度为2的特例就是现在常常使用的“正交试验设计”。50年代起，博克斯（G. E. P. Box）系统地发展了正交试验设计方法，使此设计方法不仅仅限于处理的比较，而且更系统地讨论了如何用序贯试验设计的方法改进流程。与此同时，日本的田口玄一（G. Taguchi）博士大力推广正交试验设计方法到实际应用部门，并在70年代提出了稳健参数设计方法（当时他自己称为“线外质量管理”）。这些都是我们现在应该掌握的统计工具。

我们回到例13—1，这里考虑两个因子，每个因子皆2水平。A：温度，低水平：700摄氏度（记作“－1”）；高水平：720摄氏度（记作“＋1”）。B：压力，低水平：1200帕（记作“－1”）；高水平：1250帕（记作“＋1”）。以产量Y为响应变量（单位：kg），试验结果原列在表13—2中，下面按因子排好，写成下表形式（见表13—5）：

表13—5　正交试验结果数据表

表中的前两列A，B是因子安排的代码计划（只有“＋1”及“－1”），第3列则只是形式上A与B代码的乘积。计算A因子的主效应时，将A列上对应于“＋1”的Y值求和（M＋＝270＋220＝490），将A列上对应于“－1”的Y值求和（M－＝230＋200＝430），除以样本量后可得A在“＋1”时的平均值（m＋＝245）和在“－1”时的平均值（m－＝215）；二者之差即为因子A的主效应（30）。同样可以求出因子B的主效应（40）。这些与用式（13—2）计算结果相同。对于A与B的交互作用项可以用同样的办法进行，结果得到AB交互效应为10，这就是用式（13—5）计算的表格化结果。

从上面这段分析可以看出，当我们按正交表的格式安排试验将使实施计划简化，使主效应和交互效应的计算简化。这就是正交设计“均衡分散，整齐可比”的优点。以上这些内容不难推广到更多因子的情形，在此不再赘述。

3．试验的安排、中心点的选取及随机化排序

对于全因子试验的安排，道理上是很简单的，但实际使用时要注意考虑如何在试验设计中贯彻三个基本原则：完全重复试验、随机化和划分区组。

如何实现“完全重复试验”呢？一种办法就是将每一个试验条件都重复2次或更多次，这样做的好处是对于试验误差估计得更准确了，但代价却是大大增加了试验次数因而增加了试验成本。另一种更巧妙的办法就是只在“中心点”处安排重复试验，通常是在中心点重复做3次或4次试验。

所谓中心点，在所有因子都是连续变量时容易找到，那就是各因子皆取其高水平与低水平的平均值。如果因子全部是离散变量时，可以选取它们各种搭配中的某一个组合作为“伪中心点”；如果因子中既有连续变量又有离散变量时，则可以对连续变量选取其平均值，离散变量选取某一个组合作为“伪中心点”（这时不必要求试验的“平衡”，强调的是确实要有“完全重复”）。

选取“中心点”并在此处安排重复试验的好处，主要是为了进行相同条件下的完全重复，因而可以估计出试验误差即随机误差。另外，由于每个连续因子的取值原来只有2个值（高水平及低水平），现在增加到了3个值，因而增加了对于响应变量可能存在的弯曲趋势估计的能力，这也是简单全面重复所不能达到的效果。而且，在把因子点试验的顺序随机化之后，如果再把在中心点处所进行的3次或4次试验安排在全部试验的开头、中间和结尾，那么这几个点的试验结果间只应存在随机误差。如果这几个试验结果呈现非常明显的上升、下降或其他不正常的趋势，则有可能帮助我们发现在试验过程中出现的不正常状况。这里我们要明确的是取中心点的最根本目的是估计随机误差，而不是用来参加对模型各系数（包括对常数项）的估计，这在用MINITAB软件计算时要与另一种估计回归方程的用途区分开来。

总之，安排每个因子取2水平，再加上中心点，则可以构成较好的全因子试验安排。在13.4节的部分因子试验中，可以采用相同方法安排中心点。

4．代码化及其计算

无论我们试验的目的是筛选因子还是建立关系式，都要建立回归方程。那么，是对原始的自变量数值直接进行回归分析好，还是先将这些数值进行代码化后再进行回归分析好呢？所谓代码化（coding），就是将该因子所取的低水平设定的代码（code）值取为－1，高水平设定的代码值取为1，中心水平定为0。经过理论上的分析后发现，将自变量代码化后有很多好处，即我们应该对代码化的数据进行回归分析。

（1）代码化后的回归方程中，自变量及交互作用项的各系数可以直接比较，系数绝对值大者之效应比系数绝对值小者之效应更重要、更显著。大家知道，对自变量原始数据所进行的回归方程中的回归系数是有单位的。在y＝a＋bx内，b的单位是［Y］/［X］，显然，X更换单位后，其系数也会更换。如果自变量不止一个，多个自变量间含义不同，量纲也不同，其回归系数之间显然是不可比的。如果代码化后，每个自变量都化为无量纲的［－1，1］间的数据，这时，各自变量间具有相同的“尺寸”，各系数之间就可以比较了。

（2）代码化后的回归方程内各项系数的估计量间是不相关的。很明显，x₁与x₁x₂之间是相关的，它们的回归系数的估计量之间也是相关的。比如，在回归方程中，保留x₁x₂项及删除此项时，x₁的回归系数肯定要发生变化，这造成了使用中的诸多不便。一旦将自变量全部代码化，则没有这个问题了，删除或增加某项对于其他项的回归系数将不会产生任何影响。

（3）在自变量代码化后，回归方程中的常数项（或称“截距”）就有了具体的物理意义。代码“－1”与“＋1”的中点恰好为“0”，而将全部自变量以“0”代入方程得到的响应变量预测值则恰好是截距值。因此，截距值是全部试验结果的平均值，也是全部试验范围中心点上的预测值。

用代码数据得到的回归方程是重要的（例如我们在判断因子或因子间的交互效应是否显著时只能使用此方程），但用原始数据得到的回归方程有时也是有意义的（例如求出最佳设置的原始值），因此我们应该熟悉真实值与代码值间的换算。

举例说明之。假定因子温度真实值的低水平是820，高水平是860，相应的代码值是－1和＋1，列出表格（见表13—6）。

表13—6　真实值与代码值换算表

记

中心值M＝（低＋高）/2

半间距D＝（高－低）/2

则有

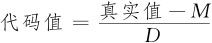
或

真实值＝M＋D×代码值

在本例中：

真实值＝840＋20×代码值

13.3.2　全因子设计的计划

全因子设计的计划中，最关键的是选定因子及确定它们的水平。先举例来说明。

例13—4

改进热处理工艺提高钢板断裂强度问题。合金钢板经热处理后将提高其抗断裂性能，但工艺参数的选择是个复杂问题。我们希望考虑可能影响断裂强度的4个因子，确认哪些因子影响确实是显著的，进而确定出最佳的工艺条件。这几个因子及准备安排的试验水平如下：

A：加热温度（摄氏度），低水平：820，高水平：860

B：加热时间（小时），低水平：2，高水平：3

C：转换时间（分钟），低水平：1.4，高水平：1.6

D：保温时间（分钟），低水平：50，高水平：60

由于要细致考虑各因子及其交互作用，我们决定采用全因子试验，并在中心点处进行3次试验，一共19次试验（即2⁴＋3），如何安排试验计划呢？

解　有了MINITAB软件的帮忙，制定试验计划就是件简单的事情了。创建试验计划的入口是“统计＞DOE＞因子＞创建因子设计（Stat＞DOE＞Factorial＞Create Factorial Design）”。进入后可得下列界面（见图13—11中左半图），在“设计类型”中选中“2水平因子（默认生成元）（2-level factorial（default generators））”，在“因子数（Number of factors）”内选中“4”。点击“设计（Design）”后可以得到图13—11中右半图，选中“全因子（Full factorial）”试验次数为“16”的那行，在“每个区组的中心点数（Number of center points）”中填写“3”，其他项可以保留默认状况（本例没有分区组，各试验点皆不需要完全复制），而后点击“确定”，得到界面见图13—12中左半图（这时图13—11中左半图内“因子”、“选项”和“结果”都由灰色变为黑色，成为可选项）。

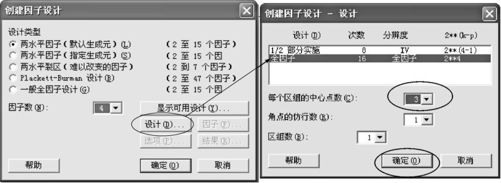
图13—11　创建全因子设计操作图1

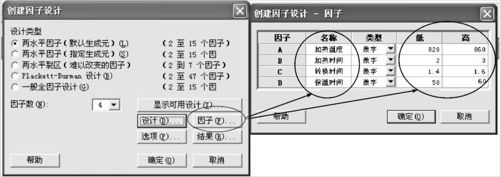
图13—12　创建全因子设计操作图2

点击“因子”打开后，可以填写4个因子的名称及相应的“低水平”及“高水平”的设置。计算机会自动对于试验顺序进行随机化，然后形成下列表格（见图13—13）。在此表的最后一列，写上响应变量名“强度”，就完成了全部试验的计划阶段工作。

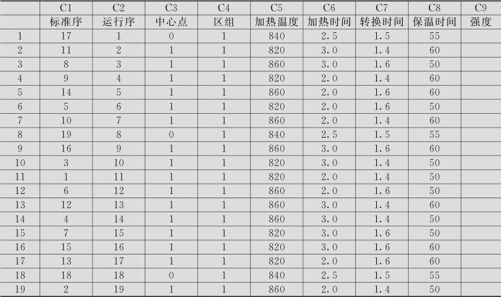
图13—13　试验计划结果图

按此表格安排试验就可以进入实施阶段了。这里要说明一点：由于试验顺序的随机化是计算机根据生成的随机数而安排的，读者得到的顺序不一定与图13—13完全相同，这其实没关系，不会影响试验的实施及对于获得数据的分析。

13.3.3　全因子设计的分析

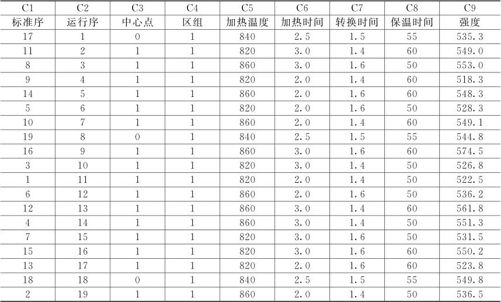
按图13—13中的试验计划表进行试验，将结果填入表的最后一列，则可得到试验的结果数据（见表13—7，数据文件：DOE_热处理（全因）.MTW）。

表13—7　热处理全因子试验结果

全因子设计的分析方法是一般的试验设计分析的典型代表，共有五大步骤。其流程见图13—14。

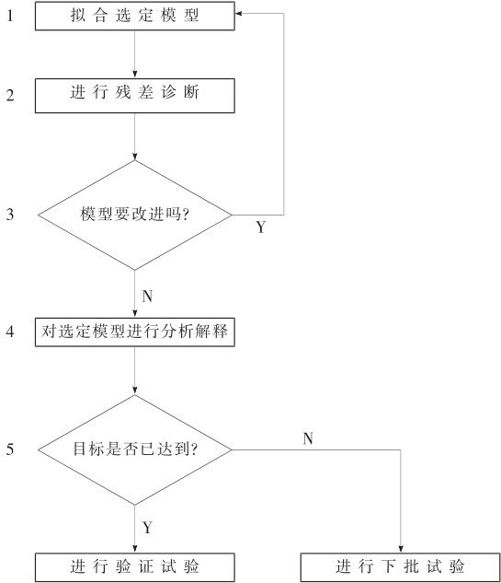
图13—14　试验设计分析五步法流程图

13.3.3.1　拟合选定模型

这里所说的第一步“拟合选定模型”，其主要任务是根据整个试验的目的，选定一个数学模型。通常首先可以选定“全模型”。由于三阶及三阶以上的交互作用通常都可以忽略不计，在因子设计的问题中，全模型就是在模型中包含全部因子的主效应及全部因子的二阶交互效应。在经过细致分析后，如果可以断言某些主效应及某些因子的二阶交互作用是不显著的，则在下次选定模型时，将不显著的主效应及二阶交互效应项删除，只保留那些效应显著的项。

拟合选定模型的操作有下列各项：

（1）从“统计＞DOE＞因子＞分析因子设计（Stat＞DOE＞Factorial＞Analyze Factorial Design）”进入，得到下列界面（见图13—15）。

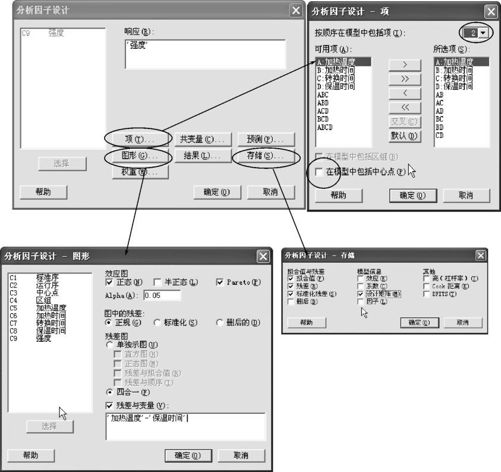
图13—15　全因子试验设计分析操作图1

（2）点击窗口“项（Terms）”后，界面如图13—15右上所示。在“按顺序在模型中包括项（Include terms in the model up through）”中选“2”（表示考虑最高到二阶交互作用，三阶及以上忽略不计）；对原默认选中的“在模型中包括中心点（Include center points in the model）”删去“选中”，而改为不选。

（3）点击“图形（Graphs）”后，界面如图13—15左下所示。在“效应图（Effects Plots）”中选“正态（Normal）”（或“半正态（Half Normal）”、“Pareto”）；在“图中的残差（Residual for Plots）”中选“正规（Regular）”；在“残差图（Residual graph）”中选“四合一（Four in one）”，在“残差与变量（Residual versus variables）”中，填写全部4个自变量名称。

（4）点击“存储（Storage）”后，界面如图13—15右下所示。在“拟合值与残差（Fits and Residual）”中选定“拟合值（Fits）”、“残差（Residuals）”及“标准化残差（Standardized residuals）”；在“模型信息（Model Information）”中选定“设计矩阵（Design matrix）”。

由于计算机的计算全部是自动进行的，其结果列在下面。我们对具体的计算过程不必过问，但对于结果要学会如何分析。

拟合因子：强度与加热温度，加热时间，转换时间，保温时间

强度的效应和系数的估计（已编码单位）

对于强度方差分析（已编码单位）

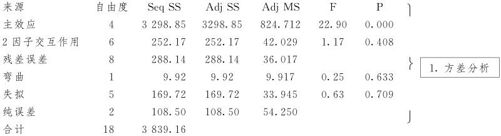
强度的系数估计，使用未编码单位的数据

第一步要注意观察在运行窗（Session Windows）的各项输出结果。由于这是对于试验结果进行回归分析，所有输出结果与第9章所介绍内容完全一致，具体含义不多重复。这里指出特别要注意下列三个要点：

分析的第一要点是分析评估回归的显著性

关于ANOVA表的分析。这里包含三点：

（1）看ANOVA表中的总效果。

H₀：模型无效H₁：模型有效

如果对应“主效应”和“2因子交互作用”中至少一项的p值＜0.05，则表明应拒绝原假设，即可以判定本模型总的说来是有效的；如果对应回归项的p值＞0.05，则表明无法拒绝原假设，即可以判定本模型总的说来是无效的。遇见这种情况就比较麻烦，这说明整个试验没有任何有意义的结果。造成这种情况的常见原因可能是下列几点：

1）试验误差太大。由于ANOVA检验的基础是将有关各项的离差平方和与随机误差的平方和相比较，取其值形成F统计量。如分母的随机误差平方和太大，则将使F变小，从而得不到“效应显著”的结论。这时，应仔细分析误差产生的各项原因，是否能设法降低，这是能找到显著因子的关键措施。当然，也有可能“试验误差太大”是由测量系统不好造成的，这时就要设法改进测量系统。

2）试验设计中漏掉了重要因子。这当然与上面一项有某种关系。漏掉了重要因子必然会使试验“误差”增大，这时更应仔细分析因子的选定。通常我们在试验前考虑因子时，很难有把握说某因子重要或不重要。这时，应该“宁多毋漏”，而不是相反。因子多选了，将来删去它很容易；一旦漏掉再想找回来就很困难了。

3）有可能是模型本身有毛病，例如模型有失拟（lack of fit），或数据本身有较强的弯曲性（curvature），这时候也可能导致判断为“模型无效”。这方面的问题将由下面讨论的两方面问题给出回答。

例13—4的ANOVA中，主效应p值为0.000，证明回归总效果是显著的。

（2）看ANOVA表中的失拟现象。

这里要检验的假设是

H₀：无失拟H₁：有失拟

在ANOVA表中，如果失拟项的p值＞0.05，则表明无法拒绝原假设，即可以判定，本模型并没有失拟现象；反之，就说明模型漏掉了重要的项（例如高阶交互作用项等），应该补上。本项计算的依据是：最初是以重复试验间的差异作为试验误差的估计（pure error），将缺失的项（例如高次项、高阶交互项等）所造成的误差平方和与之相比，经过F检验即可判明。以后，将判明为不显著的各项都归并为随机误差项，重新计算失拟项是否显著。

例13—4的ANOVA中，失拟项p值为0.709，无法拒绝原假设，可以认为回归并无失拟现象。

（3）看ANOVA表中的弯曲项。

这里要检验的假设是

H₀：无弯曲H₁：有弯曲

在ANOVA表中，如果弯曲项的p值＞0.05，则表明无法拒绝原假设，即可以判定本模型并没有弯曲现象；反之，就说明数据呈现弯曲，而模型中并没有平方项，应该补上。本项计算的依据是：最初是以重复试验间的差异及失拟项的误差作为试验误差的估计，将高低水平的2个数据连同中心点的试验数据，构成自变量的3个不同的观测值，扣除线性项后可得二次项的平方和，将二次项误差的均方和与试验误差的均方和相比较，经过F检验即可判明是否呈现弯曲。

例13—4的ANOVA中，弯曲项p值为0.633，无法拒绝原假设，可以认为本数据并无弯曲现象。

分析的第二要点是分析评估回归的总效果

（1）两个确定系数R²及。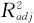

拟合的总效果可以用确定系数（coefficient of determination）R²（也称为多元全相关系数（multiple correlation coefficient））及调整的确定系数（adjusted coefficient of determination）（也称为调整的多元全相关系数（adjusted multiple correlation coefficient））。我们回顾在第9章介绍过的有关主要结论。

由回归分析中的平方和分解公式可知：

考虑SS_Model在SS_Total中的比率，定义R平方（R-Square，R-Sq）：

显然，此数值越接近于1就越好。容易看出，它有另一种写法：

由于R²有一个缺点：当自变量个数增加时，不管增加的这个自变量效应是否显著，R²都会增大一些，为此，我们引入调整的R²即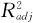，它的定义是：

式中，n为观测值总个数；p为回归方程中的总项数（包含常数项在内）。也就是说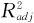，（即R-Sq（adj））是扣除了回归方程中所受到的包含项数的影响的相关系数，因而可以更准确地反映模型的好坏。因为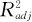总比R²要稍小一些，因此在实际应用中，要判断两个模型的优劣可以从二者的接近程度来判断：二者之差越小说明模型越好。我们常常比较包含所有自变量有关项的“全模型”与删去所有影响不显著的项后的“缩减模型”，看看究竟哪个更好。如果将影响不显著的项删去之后，二者更接近，则说明删去这些项确实使模型得到了改进。

例13—4的计算结果显示，R-Sq＝92.49％，R-Sq（adj）＝83.11％，二者间差距较大，说明模型还有改进余地。

（2）对于S值或S²的分析。

我们考虑到，所有的观测值与理论模型之间可以有误差，但总是假定这个误差应该服从以0为均值以σ²为方差的正态分布。在ANOVA表中，对应于残差误差（residual error）那行中的平均离差平方和（adj MS）的数值则恰好是σ²的无偏估计量，我们将其记为均方误MSE（mean square of error），而此量与其平方根S一并输出，可以认为S值是σ的估计。比较两个模型的优劣最关键的指标就可以选择S或S²，哪个模型能使之达到最小，哪个模型就最好。

例13—4的计算结果显示，SSE＝288.14（注意，MINITAB输出了连续平方和（sequential sum of square）以及调整的平方和（adjusted sum of square），在设计是正交的且不包含共变量的情况下，二者总是相同的），我们用SSE作为SS_Error的缩写，代表实际观测值与拟合值之差的平方和；除以自由度后得到平均离差平方和MSE＝36.017，这是σ²的无偏估计量；求其算术根得到S＝6.00146，这是σ的估计量。此量暂存作为记录，等修改模型后再来看此数值是否有所降低，以判断模型是否确有改进。

（3）对于预测结果的整体估计。

可以设想，如果有某个点在模型中起着特别重要的作用，此点可能是异常点（或离群点，指的不是数据过大或过小，而是指远离模型），或者是强影响点，或是杠杆点，此点将对于回归方程各系数的估计起着强烈的影响作用，一旦被删除，方程会有较大变化；如果某个点是个普通点，则它在模型中起着微不足道的作用，即此点对于回归方程几乎不起作用，一旦被删除，方程几乎没有变化。我们特别要警惕得到的方程是受个别点影响而形成的“虚假”回归方程。这种方程从表面上看，可能拟合得还不错，但用作预测则效果并不好。为了鉴别回归方程究竟是不是虚假的，引入两个有用的统计量，一个是PRESS，另一个是R-Sq（预测）。

PRESS是预测的误差平方和（predicted residual error sum of square），它与原来的SSE很相似，但它参加求和的各项“残差”已与原来的定义不同。这里对于第i个观测值的预测值所使用的回归方程不是用全部观测值来获得的，而是将第i个观测值删除后拟合的回归方程，然后求出其残差。对所有的观测值都是这样处理的，即轮番删除一个，计算出一个残差。最后把这些残差求出平方和来，这就是PRESS。用全部观测值来获得的回归方程，当然它肯定会受到第i个观测值的影响，会使回归方程有向此实际观测值“靠拢”的效果，因而残差会小些；删除第i个观测值后则会“客观”得多，它避免了第i个观测值本身的影响，特别当第i个观测值有强影响的时候。PRESS通常要比SSE大些。但如果大得不多，则表明数据点中有特殊地位的点不多，或它们的影响不大（保留第i个观测值与删除第i个观测值对回归方程几乎没什么影响），将来用此回归方程作预测结果也比较可信。

另一个统计量是“预测的R²”。回顾式（13—8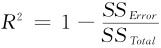），，这里的分子是SSE，是使用全部数据拟合的回归方程后得到的残差平方和。将SSE换成PRESS，则可以得到预测的R²，简记为R-Sq（预测）。此值通常会比R²（即R-Sq）要小些。但如果小得不多，则表明数据点中有特殊地位的点不多，或它们的影响不大（保留第i个观测值与删除第i个观测值对回归方程几乎没什么影响），将来用回归方程作预测结果也比较可信。

例13—4的计算结果显示，R-Sq＝92.49％，R-Sq（预测）＝53.68％，二者间差距较大；SSE＝288.14，PRESS＝1778.45，二者间差距也较大。说明本例中如果使用现在的模型，则有较多的点与模型差距较大，模型还应进一步改进。

PRESS及R-Sq（预测）的输出丰富了计算结果的信息，对进一步分析和改进模型提供了指导。

分析的第三要点是分析评估各项效应的显著性

正如南郭先生本不会吹竽，但混在齐宣王的乐队中可以“滥竽充数”，可是在齐宣王的儿子齐湣王要他独奏的时候就露出原形了。我们前面所进行的分析都是针对总效果而言的，为了把所有的效应不显著者全都删除，就要对各项效应的显著性进行逐个检验。检验的假设问题是：

H₀：β_i＝0H₁：β_i≠0

这里的β_i既可以代表某因子的回归系数，也可以代表2因子交互效应项的回归系数。如果原假设被拒绝，则说明此项作用确实是显著的，应予以保留；如果原假设无法拒绝，则说明此项作用是不显著的，应予以删除。检验的统计量是t统计量：

在原假设成立时，它是t（n－p）分布，这里n为试验次数，p是方程中包含的项数（常数项应计算在内）。

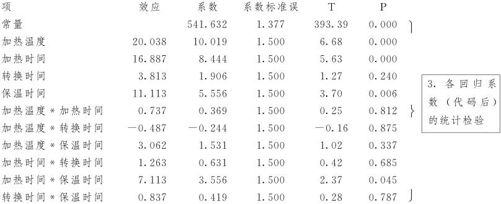
在MINITAB结果输出的最开始部分就有各回归系数（代码后）的统计检验。这里列出了各项的效应、回归系数、回归系数的标准误及检验结果。这是对各项的分别的检验，很可能有些项是显著的而另一些项不显著，将来修改模型时，应该将这些不显著项删除。要注意的是：如果一个高阶项是显著的，则此高阶项所包含的低阶项也必须包含在模型中。例如，二阶交互作用BC项显著，则B及C这两个主效应项也一定要包含在模型中，即使表面上看这两个主效应项本身并不显著。

例13—4的计算结果显示，4个主效应中，加热温度（因子A）、加热时间（因子B）及保温时间（因子D）都是显著的，只有转换时间（因子C）效应不显著。6个2因子交互效应项中，只有加热时间保温时间（BD）显著。说明本例全模型中还有不显著的自变量及2因子交互作用，改进模型时应该将它们删除。

对于各项效应的显著性，计算机还输出一些辅助图形帮助我们判断有关结论。这里最重要的就是Pareto效应图（Pareto effect plot）、正态效应图（normal effect plot）及半正态效应图（half-normal effect plot）。

Pareto效应图是将各效应的t检验所获得的t值的绝对值作为纵坐标，按照绝对值的大小排列起来，根据选定的显著性水平α，给出t值的临界值（注意按t的双侧拒绝域），绝对值超过临界值的效应将被选中（见图13—16）。

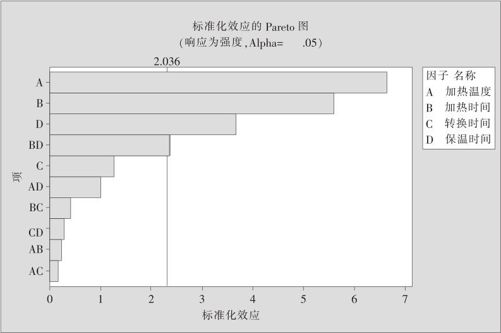
图13—16　因子效应的Pareto图

例13—4的计算结果显示，加热温度（因子A）、加热时间（因子B）及保温时间（因子D）及加热时间保温时间（BD）显著。图13—16更直观地说明了这种判断是正确的。

用Pareto效应图来判断因子效应的显著性是非常直观的，但它有个严重缺点，那就是进行各效应的t检验时，首先要用S²估计出σ²，而通常S²并不一定可靠，因此在数据与模型拟合不好的情况下，Pareto效应图不一定准确。为了更保险地删除不显著变量，还有另两张图供参考。

我们将各因子的效应按由小到大（正负号考虑在内）排成序列，将这些效应点标在正态概率图上，这就是正态效应图，示例参见图13—17。正态效应图的原理是：可以假定大多数因子中只会有极少数因子效应是显著的，即一般应遵循“效应稀疏原则”（effect sparsity principle）。因此，当挑选位于中间的一些效应的点群拟合一条直线，它们的效应应该是不显著的，效应应该服从正态分布，点全在直线上；某些效应确实非零时，相应的估计效应绝对值应会偏大，即一定会远离直线。对于正效应，估计的效应将落在直线的右（下）方；对于负效应，估计的效应将落在直线的左（上）方。在MINITAB画出的图中，凡因子效应点离直线不远者，用不标注变量名的黑圆点表示，这些点就显示它们的效应不显著；凡因子效应点离直线较远者，用标注变量名的红色正方形点表示，这些点就显示它们的效应是显著的。

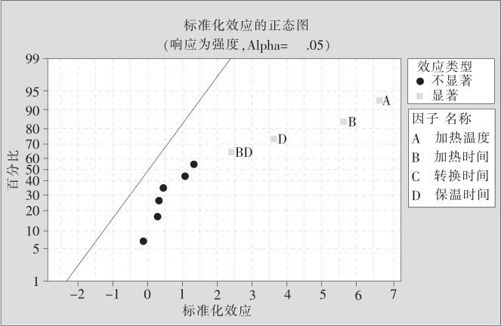
图13—17　因子效应的正态图

半正态效应图（见图13—18）与正态效应图含义完全相同，但所有效应只考虑其绝对值，因而画出的图中只有右（下）侧的点出现。与正态效应图相同，凡因子效应点离直线不远者，就应认为它们的效应不显著；凡因子效应点离直线较远者，就应认为它们的效应是显著的。正态和半正态这两张图作用相同，只画一张就够了，通常是画正态效应图。

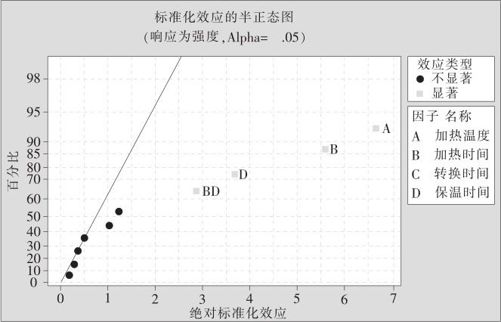
图13—18　因子效应的半正态图

例13—4的计算结果显示，加热温度（因子A）、加热时间（因子B）、保温时间（因子D）及加热时间保温时间（BD）显著。图13—17与图13—18都直观地说明了这种判断是正确的。由于本例的各主要效应项都是正的，因此两张图几乎完全一样，一般情况是不会这样的。

经过上述各项计算，我们就完成了对数据的初步分析，即第一步“拟合设定模型”的任务。

13.3.3.2　残差诊断

DOE分析“五步法”中的第二步是进行残差诊断。这一步的主要目的是基于残差的状况来诊断模型是否与数据拟合得很好。单纯从ANOVA表及回归系数的估计与检验系数两方面结果来分析整个结果是远远不完整的。为了弥补第一步所得结果的不足，我们要进行残差的诊断。如果数据与模型的拟合是正常的，则残差应该是正常的。

如何判断残差是正常的呢？我们通常假定，数据是相互独立的，且其分布为N（f（x），σ²），即这些数据是以模型为均值，以固定常数σ²为方差的正态分布。我们定义的残差（residual）是观测到的响应变量数据与代入回归模型后的预测值之差，因此，应该有：residual～N（0，σ²）。我们应该观察一下，残差是否真的这样分布。如果确实是这样分布，则可以相信选定的模型是正确的，否则就说明选定的模型不正确，要对模型进行某些修改。由于我们事先对选定的试验设计的线性回归模型没有绝对的把握，因此，残差诊断还是很有必要的。这里进行的残差诊断比一般的回归分析中的残差诊断多了一个有利条件，这就是中心点重复试验提供的残差是随机误差的正常状况，比较时可以拿中心点的残差作为比较的基准（参看图13—19及图13—20中的中心点残差）。

具体地说，残差诊断应包括下列四个步骤，观察计算机自动输出的四个图形。在对话窗“图形（Graphs）”中可以选定相应项（参见图13—15），得到下列图形：

（1）在“四合一”图的右下角图中，观察残差对于以观测值顺序为横轴的散点图，重点考察此散点图中，各点是否随机地在水平轴上下无规则地波动。

（2）在“四合一”图的右上角图中，观察残差对于以响应变量拟合预测值为横轴的散点图，重点考察此散点图中，残差是否保持等方差性，即是否有“漏斗形”或“喇叭形”。

（3）在“四合一”图的左上角正态概率图（或左下角直方图）中，观察残差的正态性检验图，看残差是否服从正态分布。

（4）观察残差对于以各自变量为横轴的散点图，重点考察此散点图中是否有弯曲趋势。

回顾第9章中介绍的残差诊断方法，如果模型与数据拟合很好，则四个图都应是正常的。什么是最常见的情况而被认为“不正常”呢？

第一种最常见残差图不正常情况是出现在第二个图中，即残差对响应变量拟合值的图中，残差未保持等方差，散点明显有“漏斗形”或“喇叭形”，这说明对响应变量y作某种变换后才会使模型拟合更好。例如，取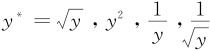，lny等作为新响应变量，可能会好得多。一般规则是这样的：如果从图中可以看出，残差的标准差σ大体上与拟合值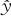的u次方成正比，则可以进行Box-Cox变换：

式中，λ＝1－u。由于人们用肉眼来判断u的取值很不容易，我们可以使用对MINITAB的补充宏指令来计算对λ的建议值。要注意的是：虽然这里变换的形式及名称都是Box-Cox变换，但这与控制图等领域中将非正态数据转换为正态数据的Box-Cox变换完全是两回事，MINITAB也并未提供相应的窗口来计算线性回归所需要的Box-Cox变换。

第二种最常见残差图不正常情况是第四个图，即残差对自变量的散点图中。残差虽保持等方差，但散点明显有U形或倒U形弯曲，这说明对响应变量y而言，对该自变量x仅取线性项已经不够了，应增加x的平方项或立方项，将会使模型拟合得更好。

例13—4的残差图见图13—19及图13—20。这些图形都显示残差是正常的。

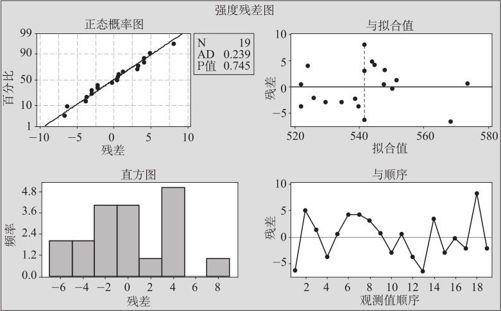
图13—19　残差诊断的四合一图

说明：有些读者发现在图13—19的左上角图中没有正态性检验的p值显示，其实只要按下列操作就可以增加此补充显示功能。从“工具＞选项＞单独图表＞残差图”进入（操作图从略）前，勾选“包括带有正态概率图的Anderson-Darling检验”就行了。

图13—20　残差对各自变量图

为了防止漏判，特别是关于残差对拟合预测值的图中是否出现了方差非齐性（喇叭口或漏斗形）的状况，可以使用下列宏指令。此宏指令与回归分析中9.3.1节及9.3.2节所介绍的内容完全一致，只不过调用格式上稍有差别而已。

调用此宏指令的格式是：

％boxcoxdoe　y　M　p　C21-C60

这里y是响应变量的变量名，可以用列号代表。M是设计矩阵，我们在最开始操作分析因子设计时，曾在“存储”项中除了“拟合值”、“残差”、“标准化残差”外，要求存储了“设计矩阵”（见图13—15右），它的具体存放位置我们可以打开“显示设计”（快捷键见图13—21）来查看。从显示结果可知我们的设计矩阵已被命名为“M1”，它共有19行（总试验次数是19），总变量个数11个（4个主效应项，6个2因子交互作用项，再加1个常数项），通常我们不必具体查看M1内容，如果需要查看M1的具体内容，可以从“数据＞显示数据（Data＞Display Data）”入口，指明显示矩阵M1就可以。设计矩阵的内容有两种形成格式，一种是由原始数据形成，另一种是由代码数据形成。在计算机内部，二者都是有用的，但究竟哪种形式称为“设计矩阵”则可以有不同的选择。如果计算中不牵涉到自变量的设定值时（例如研究是否需要对响应变量做变换）则不必注意其定义是哪种选择；如果计算中牵涉到自变量的设定值时（例如对给定的自变量值进行预测计算）则必须注意其定义是哪种选择。MINITAB R15设计矩阵显示的是原始数据，自变量的设定值必须使用原始数据的值；MINITAB R16设计矩阵显示的是代码数据，自变量的设定值必须使用代码数据的值。最后要为计算机留出可供随意使用的40个空白列（“40”是事先设定的，不能多也不能少）。

图13—21　查看设计矩阵位置操作图

在例13—4中，调用命令是从“编辑＞命令行编辑器（Edit＞Command Line Edit）”入口，输入下列命令（参见图13—22）：

％boxcoxdoe　C9　M1　11　C21-C60

图13—22　调用Box-Cox变换宏指令操作图

结果可以看到输出图形如下（见图13—23）。

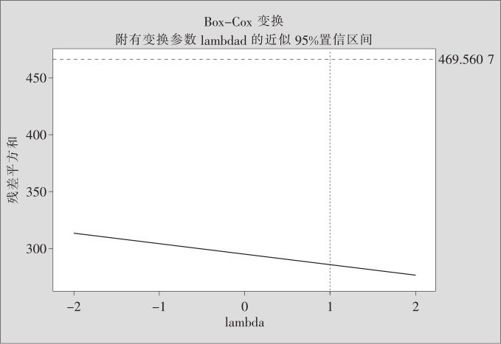
图13—23　调用Box-Cox变换宏指令结果图

这里的横轴是Box-Cox变换的方幂λ，纵轴是按此λ进行响应变量变换后所形成的残差平方和，曲线用蓝色实线显示。图形最上方的红色虚线表示符合方差齐性要求的残差平方和上限，如果残差平方和蓝色曲线落在红色虚线下方，则表示用此λ值进行变换已经可以使残差达到齐性。而当λ＝1时，表示不必进行变换。因此分析此图关键是看在λ＝1处，残差平方和蓝色曲线是否落在红色虚线下方。如果残差平方和蓝色曲线确实落在红色虚线下方，则不必对y进行变换；反之，则需要进行变换，而对于λ的选择则只要寻求蓝色曲线的最低点附近的λ即可。将响应变量进行变换后，一切都要从头开始，重新拟合模型。

对于例13—4，在图13—23中发现在λ＝1处，残差平方和蓝色曲线确实落在红色虚线下方（见图13—23中竖直虚线），说明方差齐性要求是满足的，不必再对y进行变换。

总之，DOE分析的第二步只是进行残差诊断，只是看“模型是否有问题”。如果确实发现了问题，又如何办呢？这就转入了第三步。

13.3.3.3　判断模型是否要改进

DOE分析“五步法”中的第三步是：判断模型是否要改进。一共有三件事情要考虑：

（1）残差对拟合预测值的诊断图中，是否有不齐性或弯曲的情形？如果此图有问题，则提示我们，要对响应变量y作某种变换后才行，将y作变换后一切重新开始。具体判断方法前段已有详细叙述。

（2）残差对自变量的诊断图中，是否有弯曲的情形？如果确实有弯曲，则要考虑增加x的平方项或立方项才会使模型拟合更好，那么就一定要修改模型（例如进行响应曲面设计，重新安排或增加试验，然后重新开始拟合）。

（3）基于各项效应及回归系数计算的显著性分析中是否有不显著项？如果发现有些主效应项或交互效应项并不显著，这些项应该从模型中删除，模型的拟合也要重新进行。

总之，凡是发现模型需要修改时，就要返回最初的第一步，重新建立模型，再重复前面所有各步骤。

在例13—4中，发现只是在模型中包含有不显著项，应予以删除。加热温度（因子A）、加热时间（因子B）、保温时间（因子D）及加热时间保温时间（BD）显著，应予以保留，其余都应删除。现在再转回13.3.3.1节。

再次从“统计＞DOE＞因子＞分析因子设计（Stat＞DOE＞Factorial＞Analyze Factorial Design）”进入，主要是修改“项（Terms）”，在选取的项中将A（加热温度）、B（加热时间）、D（保温时间）及BD保留，其他项皆删去，操作中的其余各项都保持不变。计算后得到下列结果：

结果：DOE_热处理（全因）.MTW

拟合因子：强度与加热温度，加热时间，保温时间

强度的效应和系数的估计（已编码单位）

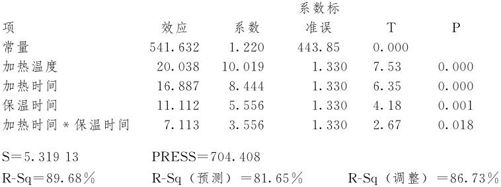
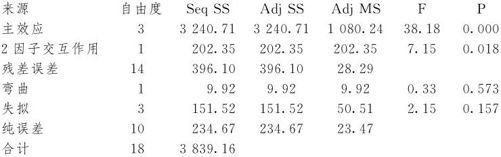
对于强度方差分析（已编码单位）

强度的系数估计，使用未编码单位的数据

对于这次计算结果，仍用前面介绍过的方法与步骤进行分析。

此时观察到下面几处要点：

先看ANOVA表中的总效果。在本例中，对应主效应项及2阶交互项的p值分别为0.000（即＜0.001）和0.018，表明应拒绝原假设，即可以判定本模型总的说来是有效的。在本例中，对应失拟项的p值为0.157，其值比临界值0.05大，表明无法拒绝原假设，即可以判定，本模型删去了好多项，但并没有造成失拟现象。再看删减后的模型是否比原来有所改进。我们把各项计算结果列在这里，用来比较全模型与删减模型哪个更好，结果见表13—8。

表13—8　全模型与删减模型效果比较表

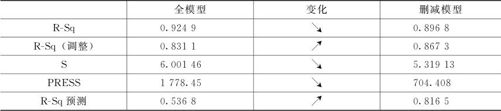
可以看出，由于模型项数减少了6项，R-Sq通常会有微小的降低（本例由0.9249降低到0.8968），但关键是看调整的R-Sq（adj）是否有所提高。本例中，R-Sq（调整）由0.8311提高到0.8673，可见删除不显著的主因子及交互作用项后，回归的效果更好了。而S的值由6.00146降为5.31913，PRESS由1778.45降到704.408，再次证明删除不显著的主因子及交互作用项后，回归的效果更好了。

对于缩减模型同样应该进行残差的诊断，但本例中所有的结果都说明模型与数据拟合得很好，残差图也全部正常。

13.3.3.4　对选定模型进行分析解释

经过前三步的多次反复，已获得一个我们认为最满意的方程，将它定为我们选定的模型。

在例13—4中，最后确认的回归方程是：

除此之外，计算机也提供最后确定了的对原始数据的回归方程：

y＝213.1＋0.5009A－61.35B－2.445D＋1.4225BD

第四步是“对选定模型进行分析解释”，主要是在拟合选定模型后输出更多的图形和信息，并作出有意义的解释。主要包含下列四个方面，而这些要求在MINITAB中都会自动给出结果。

1．再次进行残差诊断

这时残差诊断的目的已与前面的残差诊断不同了。前面的诊断着重考虑模型是否与数据拟合得合适，如何修改模型以求拟合得更好；本阶段的诊断则是在肯定模型不再修改的前提下，判断数据中是否有个别点出现异常。

检验的方法是将分析“正规（Regular）”残差换为分析“标准化（Standardized）”残差，后者在一般教材中称为“t化残差”，它不是简单地把残差减均值并除以残差的标准差，它还要考虑到自变量观测值到自变量平均值之间的距离等因素而得到的（具体计算公式从略）。标准化后的残差可以近似看成相互独立的服从标准正态分布的随机变量，因此标准化残差的绝对值一般不应超过2（标准正态分布落在±2之外的概率大约只有5％），这可以用来检查单个观测值是否有异常（注意这种“异常”不是指观测值是否过大或过小，而是指偏离模型是否很远）。

也可以将“正规（Regular）”残差换为“删后（Deleted）”残差，删后残差是指在全部数据中删除本数据而保留别的数据再进行回归时，对本观测值所得到的残差。删后残差的平方和就是前面提到的PRESS。

如果在实际问题中遇到异常点或强影响点，要考虑到它对估计和拟合的种种影响。解决问题的办法有两种：一是观察删除此点后方程究竟会如何；二是采用一些不大受这种点影响的“稳健”估计方法，主要有R方法（采用数据的秩数据）和M方法（休伯（Hu-ber）提出的一种极大似然估计方法）。有需求的读者可以参考相关专门书籍（如参考文献［3］：茆诗松主编的《统计手册》等），这里不多陈述了。

具体做法是：打开原数据文件，可以看到在拟合最后选定的模型后所形成的“标准化残差”列，仔细察看此列数据。如果全部数值之绝对值都不超过2，则可认为“无异常点”；如果个别数据绝对值超过2，则可认为“此点可能异常”。当然，如果绝对值超过2的点数不超过总点数的5％，则异常的情况并不严重。

在例13—4中，所有标准化残差数据都是正常的。

2．确认主效应及交互效应的显著性，并考虑最优设置

输出各因子的主效应图、交互效应图。在MINITAB软件中可以从“统计＞DOE＞因子＞因子图（Stat＞DOE＞Factorial＞Factorial Plot）”进入，设定各因子的主效应图、交互效应图的设置（“立方图”通常不用显示，除非交互作用太严重，简单效应分析找不到最优点时才用）。我们可以从图中看到，已经选中的那些主因子和交互作用项是否真的很显著，未选中的那些主因子和交互作用项是否真的不显著，从而更具体、更直观地确认选定模型。

在例13—4中，我们考察4个因子，希望断裂强度最大。主效应图见图13—24。

图13—24　断裂强度的主效应图

从图13—24中可以看出，因子A（加热温度）、B（加热时间）、D（保温时间）三者回归线较陡，故主效应影响确实显著；而因子C（转换时间）回归线较平，故主效应影响确实不显著。为了使断裂强度达到最大，三因子都是取值越大越好，即因子A（加热温度）应取上限860摄氏度，因子B（加热时间）应取上限3小时，因子D（保温时间）应取上限60分钟。

从图13—25中可以看出，只有因子B（加热时间）与因子D（保温时间）二者效应线明显不平行，说明二者交互作用显著。

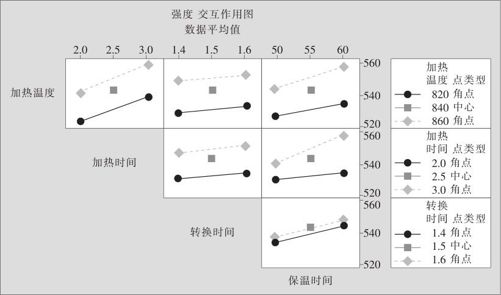
图13—25　断裂强度的交互效应图

3．输出等值线图、响应曲面图等以确认最佳设置

我们绘制等值线图及响应曲面图的目的是进一步确认，响应变量是如何受所选中的那些主因子和交互作用项的影响的，它的变化规律如何。在自变量的主效应与交互效应图中我们已经获得一些最佳设置的信息，但这些分析是否准确？我们可以从等值线图及响应曲面图中，直观地看到整个试验范围内的最佳值的位置。

众所周知，等值线图及响应曲面图只能同时考虑两个自变量及一个响应变量。如果自变量个数较多，只能分多组进行，MINITAB也确实设定可以“对所有配对变量绘制等值线图及响应曲面图”。但实际应用中，如果两个自变量间无交互作用时，等值线图是一组平行线，响应曲面图是平面，几乎不增加新的信息。因此为了集中精力研究变化规律，最重要的只需绘制有交互作用的那些自变量就够了。

在例13—4中，只有因子B（加热时间）与因子D（保温时间）二者交互作用显著，我们绘制这组等值线图及响应曲面图，而设定另一个影响显著的变量A（加热温度）为最佳设置（取最大值860摄氏度）。具体操作如下：从“统计＞DOE＞因子＞等值线／曲面图（Stat＞DOE＞Factorial＞Counter/Surface Plot）”进入，在设置后就可以获得结果了（等值线图见图13—26，曲面图见图13—27）。

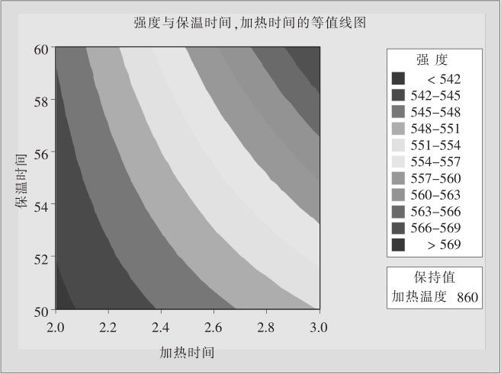
图13—26　断裂强度的等值线图

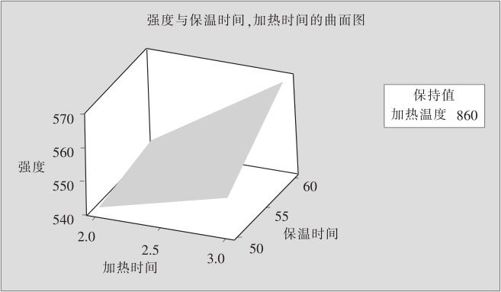
图13—27　断裂强度的曲面图

从图13—26及图13—27中可以看出，断裂强度的最大值确实在B（加热时间）＝3小时，因子D（保温时间）＝60分钟，因子A（加热温度）固定在860摄氏度时达到最大（等值线图中右上角之点）。在MINITAB软件实际绘制的等值线图内，蓝色代表低值，绿色代表高值，高低状况一目了然；本书是黑白两色显示，高低状况不很清楚，但结合曲面图仍可以准确判断出来。

4．实现最优化

在设定的最佳条件下，究竟响应变量可以取什么结果？是否真的是最优？我们应按照具体问题的望大、望小或望目特性在整个试验区域内求得响应变量的最优值。虽然在因子设计阶段，我们的试验设计的主要目标是筛选变量，但根据对于数据的分析，已经可以判断出哪些自变量效应是显著的，哪些自变量效应是不显著的，我们可以在使用这些信息的基础上，获得最佳值。在MINITAB软件中有专门的响应变量优化器窗口。使用时，可以从“统计＞DOE＞因子＞响应优化器（Stat＞DOE＞Factorial＞Response Optimizer）”进入（见图13—28），计算机可以自动给出最优设置。只要在使用前选定响应变量（见图13—28中左）后，再对最优的目标予以设置（见图13—28右）即可。

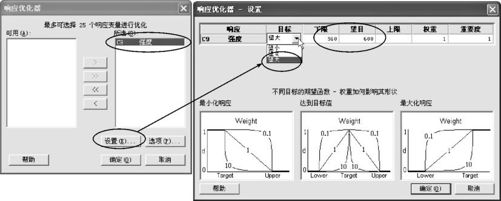
图13—28　对断裂强度使用响应变量优化器

根据具体问题要求，优化目标有望大型、望小型和望目型三种。设置时先要选定目标的类型。如果是属于望大型的，在对最优的“目标（Goal）”设定上，取“望大（Maxi-mize）”，在“设置（Setup）”中，只需填写“下限（Lower）”及“望目（Target）”两项，而“上限（Upper）”留为空白。这时，填写的“下限”一定要取试验中已经确实达到的结果（计算机将以此点作为起始点，不要选得太大）；填写的“望目（Target）”一定要远远高于可能达到的最大值（计算机一旦达到此值将立即停止搜索，所以要把目标设得高高的）。如果是属于望小型的，在对最优的“目标（Goal）”设定上，取“望小（Minimize）”，在“设置（Setup）”中，只需填写“上限（Upper）”及“望目（Target）”两项，而“下限（Lower）”留为空白。如果是属于望目型的，在对最优的“目标（Goal）”设定上，三个值都要设定：“望目（Target）”填写目标值，“下限（Lower）”及“上限（Upper）”则填写容许的范围。由于计算机的计算要兼顾这三种不同的需求，为此，通常要把求响应变量Y达到最优的问题转化为求一个渴求函数（desirability function）的单个合意度（desirability）d（0≤d≤1）达到最大的问题。d的取值越接近于1表示越满意，d的取值越接近于0表示越不满意。这个渴求函数的具体设置是计算机根据望大、望小或望目三种不同情况自动设置的，若响应变量y的估计值为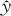，设定的权重为r，合意度d的定义如下：

（1）望大型：设下界为L，目标为T，则

（2）望小型：设目标为T，上界为H，则

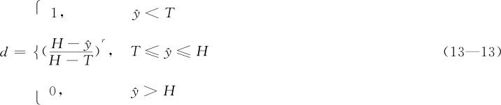
（3）望目型：设下界为L，目标为T，上界为H，则

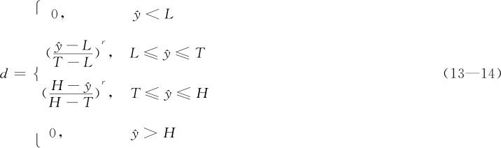
对同一个问题，如果对于下界L、目标T、上界H的这几个值的设定不同，则合意度可能不同，但最终的最优解是不受影响的。“权重（Weight）”取值r的范围是0.1～10，通常设定（即默认值）为r＝1。小于1时将减小对目标的强调；等于1时将目标和上下限视为同等重要；大于1时将加大对目标的强调。权重的含义在图13—28中右图下端给出了形象的描述，r值只在有特殊要求时才需要修正。计算机自动搜索后，将得到d达到最大值的结果。如果同时考虑多个目标（本窗口号称可以同时处理25个响应变量），则使用者可以按重要性赋予不同的重视程度。如果同时考虑k个响应变量的优化问题，当第i个响应变量的“重要性（Importance）”取值为w_i（其设定范围是0.1～10）时，则可以将各自的合意度d_i组合成为一个综合指标：复合合意度D。其定义为：

式中，W＝∑w_i，是所有重要性的总和。这时，D相当于对各个d_i以w_i为权重的几何平均值。特别地，如果这些权重全部相等，则式（13—15）可以简化为这些合意度d_i的简单几何平均值：

对于只有单个响应变量的情况时，根本不必设定重要性，保持默认的w_i＝1就行了。

在例13—4中，问题是属于望大型的，在对最优的“目标（Goal）”设定上，取“望大（Maximize）”，在“设置（Setup）”中，填写“下限（Lower）”取“560”（这个值是在做过的试验中已经实现了的），取“望目（Target）”为“600”（这个值是在做过的试验中未能达到的，是较高理想），“上限（Upper）”留为空白。计算结果见图13—29。

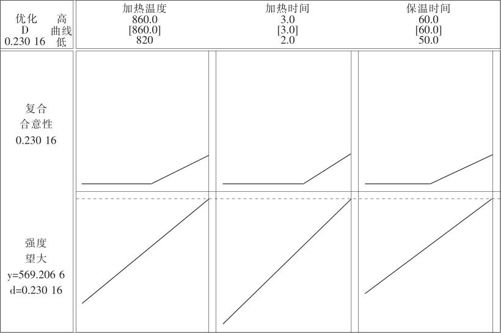
图13—29　断裂强度响应变量优化器结果图

这个图中共有3列，分别是我们选中的自变量。最上端列出各变量名称、取值范围及最优设置（用中括号括起）。上半图是合意度d的取值情况，下半图是最优化结果：最大值在因子A（加热温度）取860摄氏度，因子B（加热时间）取3小时，因子D（保温时间）取60分钟时达到，断裂强度最终可以达到569.2066。合意度d＝0.23016（所填写的上下限有变化时，此值可能也变）。

响应变量优化器可以进行人机对话，图中的各项设置都是可以调整的。每个自变量的设置值（竖直红线）可以用鼠标拖动，也可以双击最上端的红色区间（用中括号表示的）直接设定数值。这可以弥补计算机考虑不周时的不足，用人工方法协助计算机完成选优工作。

这里要对例13—4中的数据再作些解释。从数据表中，我们明明看到已达到的最大值是第9号试验点的y＝574.5，为什么计算出的最优值却只有569.2？实际上，由于自变量C（转换时间）作用不显著，而试验数据中对应A（加热温度）取860摄氏度，因子B（加热时间）取3小时，因子D（保温时间）取60分钟的试验一共进行了两次，除了第9号试验外，第13号试验条件也如此（只是C（转换时间）不同），但13号试验结果只为561.8，我们不能只看好的，而应考虑在此试验条件下所有可能取值的平均状况。我们预测的最优值569.2066是有道理的。

13.3.3.5　进行验证试验

DOE分析“五步法”中的第五步是判断“目标是否已达到？”这主要是将预计的最佳值与原试验目标相比较。如果离目标尚远，则应考虑安排新一轮试验，通常是在本次获得的或预计的最佳点附近，重新选定试验的各因子及其水平，继续做因子设计DOE或回归设计（RSM），以获得更好的结果。如果已基本达到目标，则要做验证试验以确保将来按最佳条件生产能获得预期效果。试验设计大师博克斯（G. Box）有句名言：“所有统计模型都是错的，只不过有些模型有用罢了”（All models are wrong, some are useful）。我们根据试验数据所建立的任何统计模型是否符合实际规律，在未验证前都是没有把握的。通常的做法是先算出在最佳点的预测值及其变动范围，然后在最佳点做若干次验证试验（通常要3次以上），如果验证试验结果的平均值落入事先计算好的范围内，则说明一切正常，模型是正确的，预测结果可信；否则就要进一步分析发生错误的原因，改进模型，再重新验证，以求得符合实际数据的统计模型。

1．直接得到预测区间

从回归分析（见9.2.6节）介绍中可以知道，预测区间分为对于理论均值的预测（95％ CI）及对于单个试验结果的预测（95％ PI）两种。前者所谓“理论均值”实际上相当于进行无穷多次试验结果的平均；后者所谓“单个试验结果”实际上相当于进行一次试验得到的值。我们下面给出MINITAB的操作步骤。

从“统计＞DOE＞因子＞分析因子设计（Stat＞DOE＞Factorial＞Analyze Factorial Design）”进入，得到如图13—30所示界面。请注意，我们在“项（Terms）”中已经将最终选定的模型中包括了因子A（加热温度）、因子B（加热时间）、因子D（保温时间）以及因子B与D的交互作用项。再打开“预测（Prediction）”窗，在“因子”设定值格内按“项（Terms）”中顺序填写最优设置即可（注意不要受“预测”窗中列出了全部变量的影响，这里不用填写交互作用项的实际数值）。

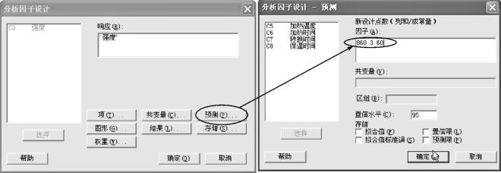
图13—30　试验设计的预测计算操作

计算机将自动给出下列数值结果：

最左侧给出的拟合预测值是569.207，就是将自变量值代入回归方程所得的结果，这与最优值的预测是一致的。拟合值标准误为2.926，是拟合值的标准差，此值在作进一步计算时还有用。预测值平均值置信区间（95.0％ CI）的结果是（562.931，575.483），表明了回归方程上的点的置信区间。对此区间可以理解为，当按照此自变量的设置无限多次重复运行下去将会获得的理论均值的95％置信范围，此值可以作为改进结果的预报写在总结报告中。在例13—4中，具体说就是：当加热温度取860摄氏度，加热时间取3小时，保温时间取60分钟时，我们可以有95％把握断言，断裂强度平均值将落入（562.931，575.483）之内。后一个置信区间95％预测区间（95.0％ PI）表明的是以上述回归方程上的点的置信区间为基础，加上单个观测值具有试验误差而给出的置信区间。这里，95％预测区间（95.0％ PI）是将来做一次验证试验时将要落入的范围，可供做验证试验时使用。换言之，当加热温度取860摄氏度，加热时间取3小时，保温时间取60分钟时，我们可以有95％把握断言，任何一块钢板的断裂强度将落入（556.186，582.227）之内。

上述结果只给出了验证试验次数m＝1及m＝∞的两种特例情况。一般验证试验要3次以上，下面还需要学会求出这m次验证试验获得的均值所应落入的置信区间。

2．任意次数验证试验平均值的预测区间

m个观测值的平均值的95％置信区间计算公式是：

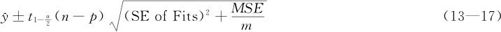
式中，n是试验总次数；p是最终模型中所包含的项数（常数项要计算在内）；m是验证试验的次数；SE of Fits是在回归方程预测值时输出的拟合值的标准误（在输出拟合值后，紧接着就有“拟合值标准误（SE of Fits）”的数值）；MSE也就是σ²的无偏估计量，它就是在ANOVA表中输出的对应“残差误差”的adj MS项。

显然，当m＝1时，此置信区间就是95％预测区间（95.0％ PI）；当m趋于无穷大时，此置信区间就是95％置信区间（95.0％ CI）；当需要求出m个（例如m＝3或m＝5）观测值平均值的95％置信区间时，只要代入相应的m的数值就行了。

在例13—4中，试验总次数n＝19，最终模型中所包含的项数（含常数项）p＝5，验证试验的次数m＝3。SE of Fit＝2.926（见刚才的预测结果），MSE＝28.29（见ANOVA表），查14个自由度的t分位数表（见本书附表3）可得

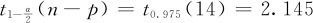
因此，变动半径的公式如下所示：

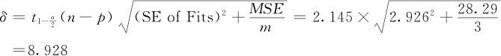
因此可知，3个观测值的平均值的95％置信区间为：

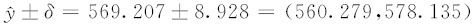
这样的计算太麻烦，为了大家使用方便，本书提供了宏指令，读者可以直接得到所要结果。

在调用宏指令之前，先要在某空白列上填写出最佳设置的数值，不但要包含自变量项，而且要含交互作用项。

在例13—4中，我们将第10行命名为“X预测”，其中有4项：860，3，60，180。其中前3项分别为加热温度、加热时间及保温时间之值，最后的值“180”是BD乘积项值。

调用宏指令格式为：

％ypred　y　M　p　m　xpred

式中，y是响应变量；M是设计矩阵；p是最后回归方程所含项数（含常数项在内）；m是准备进行的验证试验的次数；xpred是自变量的最佳设置。请注意，由于MINITAB R15与R16在程序中有变化，在因子设计时，R15的设计矩阵一律使用原始数据形成，而R16则一律换用代码数据，因此我们在进行预测结果的计算时，就要用不同的预测自变量数据。为了避免混淆，最好先输出设计矩阵来看一下（从“数据＞显示数据（Data＞Display Data）”入口，指明显示矩阵M1就可以）。对于例13－4，下面分别显示出R15及R16的设计矩阵内容：

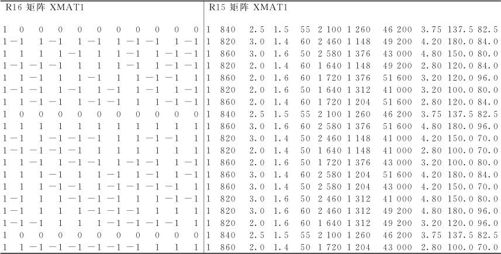
我们在数据文件“DOE_热处理（全因）.MTW”中的C10中，给出了用原始数据表示的有显著效应的自变量最佳设置点：A加热温度为860（℃），B加热时间为3（小时），D保温时间为60（分钟），加上显著的交互作用BD，自变量最佳点的设置为“860，3，60，180”。C10这一列是在用MINITAB R15版本时使用的，换用R16时，则要使用C11列，那里是代码化的设置“1，1，1，1”。具体到例13—4，如果使用MINITAB R15，则调用宏指令的命令为：

％ypred　C9　M2　5　3　C10

如果使用MINITAB R16，则调用宏指令的命令要换为：

％ypred　C9　M2　5　3　C11

不论哪个版本的MINITAB，计算结果都是相同的。

最后结果表明，如果验证试验重复进行3次，则其平均值应落入（560.109，578.304）之内。如果平均值确实落入此区间，则说明试验结果分析及预测等结论都是可信的。

实际计算时，为了避免出错，在调用宏指令时，可以先令m＝1，这时得到的结果应该与计算机算出的95％预测区间（95％ PI）一致，然后再来计算自己设定的m值。

13.3.4　全因子设计的补充介绍

在上节我们介绍了最常见的全因子设计方法。实际上，全因子设计方法内容非常丰富，本节将补充介绍下列常见情况，包括：（1）无中心点重复的计算例题；（2）含离散型变量为因子的例题；（3）响应变量需要变换的例题；（4）离散型响应变量的处理方法；（5）带区组的例题。

13.3.4.1　无中心点的试验及分析

作为因子设计，使用博克斯推荐的设计点加上若干中心点的方法是最有效的方法。但有些时候，进行中心点的试验很困难或很麻烦，不希望进行中心点的试验；有时试验中含有离散因子，根本就没有“中心点”可言，这时当然可以考虑选择使用“伪中心点”，但也可以放弃安排伪中心点处的试验；解决此问题的通用选择就是进行重复试验。这时，我们可以只在因子点上仿行（即“重复”）一次，分析方法基本上与含中心点的试验相同，下面举例说明。

例13—5

铣床加工精度分析试验。为了保证精密轴孔的光洁度（用平面度来度量），在加工轴孔时要进行最后一道工序——铣床加工。在铣孔的过程中，影响平面度的最重要因子有A“转速”，B铣刀的“进刀速度”及C“润滑油进给量”。调整铣床的参数较困难，如果增加中心点的试验则要多增加一次调整铣床时间，因此免去中心点的试验安排。为实现重复，则每个试验点皆重复一次。本来按随机化要求，要将所有试验次序全部随机排序，但这样做，又会增加试验时间。为此，考虑到，由于整个加工试验时间不需要太长，按同一参数连续加工两个零件不会影响随机化，因此最后决定进行3因子2水平不含中心点仿行1次的全因子试验，且仿行是两次连续进行的。A：转速的高水平为860（转／分钟），低水平为800（转／分钟）；B：铣刀的进刀速度高水平为1.5（mm／秒），低水平为1.0（mm／秒）；C：润滑油进给量高水平为7（毫升／秒），低水平为6（毫升／秒）。试验结果列在表13—9中（数据文件：DOE_铣孔（无中心点）.MTW）。

表13—9　铣床加工精度分析试验数据表

解　下面给出分析结果。实际上，不含中心点的试验结果之分析过程与一般全因子试验（如例13—4）完全相同。由于不含中心点，因此在分析结果时无法估计出是否有弯曲，除此之外所得的结果与含中心点的一般全因子试验完全相同。这点反映在方差分析表中。本例的一般结果从略，其方差分析表为：

平面度的方差分析（已编码单位）

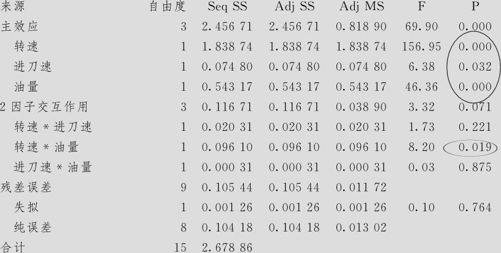
在此处的方差分析表中，在残差误差的组成项中，除纯误差项外，只含有“失拟”项的估计，根本没有“弯曲”项的估计值。在进行试验前，对此应考虑清楚。在本例中，安排中心点当然会增加完成试验的难度（多调整一次参数的设计值），但好处却是可以估计是否有弯曲。如果事先能肯定不存在弯曲时，不安排中心点则无任何问题；反之，不能肯定是否存在弯曲时，则还是应该安排中心点的试验的，且这样做的结果在总试验次数上还是合算的。本例后续的结果分析在此全部从略，大家不难自行完成。

13.3.4.2　含离散因子的试验及分析

前面几个例子中，我们所举的自变量全部是连续型的。但实际工作中有可能出现离散因子（即离散型自变量）的情况。下面举例说明自变量中若同时含有连续型和离散型两种情况时，应该如何处理。

例13—6

提高合成氨产量试验。为了提高合成氨的产量，要选择最佳工艺条件，这里含3个重要因子：A反应温度（Temp）、B反应时间（Time）及C催化剂种类。这里，A及B皆为连续型自变量，而C为离散变量（1号及2号催化剂两种）。安排含4次中心点的2水平全因子试验，且两种催化剂各试验两次。A：反应温度的高水平为780℃，低水平为760℃；B：反应时间高水平为44分钟，低水平为40分钟；C：催化剂高水平为2号催化剂，低水平为1号催化剂。响应变量为产量（单位：千克）。试验结果列在表13—10中（数据文件：DOE_合成氨（含离散因子）.MTW）。

表13—10　合成氨试验数据表

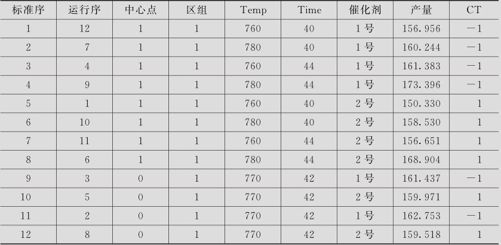
解　本例与一般的全部为连续型因子试验在分析时的最大不同是回归方程有变化，同时在绘制残差分析图的操作中有不同（CT含义及详细操作见下面的解释）。

本例的计算结果输出表是这样的：

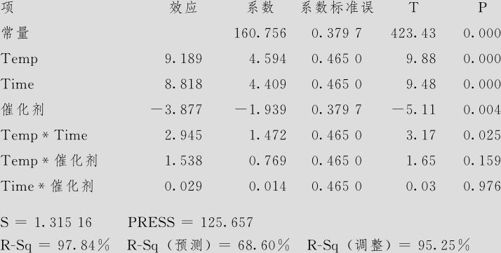
产量的估计效应和系数（已编码单位）

产量的方差分析（已编码单位）

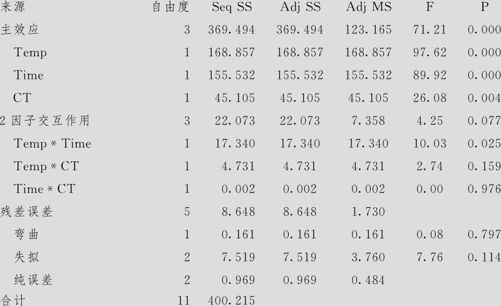
从方差分析表中可以看出，数据并无弯曲及失拟，因此可以直接分析各因子的响应。这里要注意的是：含离散因子的方程解读与全部是连续因子的情况有所不同。上面各因子效应的分析中，结果看似无任何特殊之处，实际则不然。本例的回归方程写出来应该是：

这就是说，含离散因子的回归方程一定会分为几叉，本例离散变量取2值，因此分两叉；有两个分别取2值的离散变量时，共分4叉，…，依此类推。当催化剂分别为1号和2号时，方程分别采用上下两不同的表达式。而且注意，在最开始得到的估计效应和系数表中的各个系数实际上相当于离散因子取第二个水平时的系数，因为效应（系数也一样）代表的是离散因子“高水平”与“低水平”的响应变量值之差，其差值为正时，代表的是的离散因子取“高水平”比取“低水平”要高，反之亦然。本例中，催化剂的系数－3.877为负，代表响应变量的值在催化剂取“高水平”（2号）要比催化剂取“低水平”（1号）低。

在进一步的分析中，发现本例中有两项交互作用项不显著，而且残差正常、不需要对y进行变换的情况，这时，在修改模型时只要去掉这两个不显著项就行了。经修改模型删除两项交互作用项后，最后可得结果如下：

因此，显著项为A（温度）、B（时间）、C（催化剂）及AB交互项，最终的回归方程为：

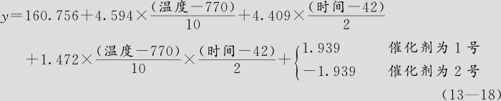
这就是说，如果温度和时间不变，只是催化剂变化时，它们的常数项要进行修改（即分别减或加某个常数，此常数即该项的“回归系数”）。这一点与回归分析是一样的，我们在9.4节Logistic回归中的例9—8中的回归方程（9—38）也列出了详细结果，不过那里已经直接给出了离散自变量取不同值时的修改结果。

另外一点不同是在含离散因子时，其绘制残差图时也有不同。由于MINITAB软件的限制，当自变量为离散型因子时，在绘制对该变量的残差图时，计算机不能直接生成残差图。补救的办法是：另加一列“连续型”的数字来代表这个离散型因子的取值就行了。本例中，新增加取名为“CT”列，它取值（按连续变量取值）为－1（催化剂为1号）及1（催化剂为2号）。从“统计＞DOE＞因子＞分析因子设计（STAT＞DOE＞Factorial＞Analyze Factorial Design）”窗口进入后，在关于“图形”的窗口（参看图13—15中左下）中，在“残差与变量”项下，需要填写的除了原来的“Temp”、“Time”外，还要增加一个“CT”（参见图13—31中左侧）。其残差输出图（参见图13—31中右侧）也与连续自变量的残差图略有不同（这里无中心点，因此只在“－1”、“1”两处有残差）。

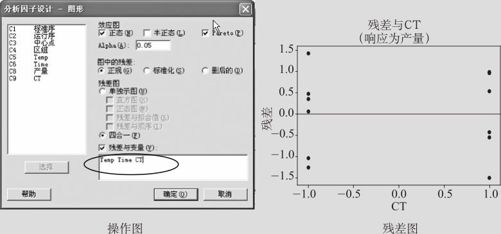
图13—31　含离散因子的残差分析操作图及残差图

对于残差的分析等项工作，并未因是否为离散因子而不同。主效应图及交互效应图分别如图13—32和图13—33所示。

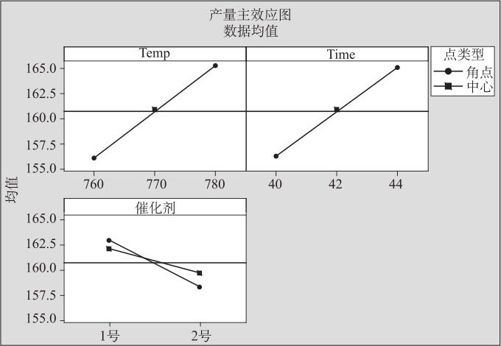
图13—32　含离散因子的主效应图

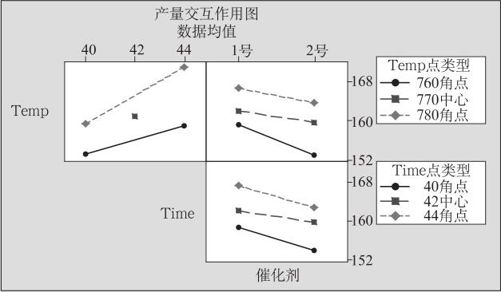
图13—33　含离散因子的交互效应图

从主效应看，三个因子效应都是显著的；除A（温度）与B（时间）之间交互作用显著外，其他各项交互作用都不太显著。

等传值线图（见图13—34）及曲面图（从略）进一步证实了上述分析。

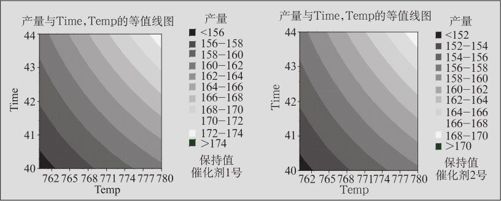
图13—34　合成氨产量的等值线图

总之，本例的结果为回归方程（13—18）。从方程中可以看出，当温度取高水平（高温：780℃）、时间取高水平（长时间：44分钟）（即等值线图中的右上角）时，等值线取最大值；仔细比较图13—34中两图，可看出当催化剂取1号时，产量可以达到最大。

13.3.4.3　响应变量需要变换的试验及分析

前面介绍的几个例题中，残差图基本上是正常的。但如果残差与自变量的残差图中出现了弯曲，就说明此时仅拟合线性方程是不够的，需要在回归方程中增加自变量的高阶项，而这只能通过增加试验点的方式实现，这就是后面介绍的响应曲面设计方法，在此不加说明。如果残差与响应变量预测值的残差图中出现了非齐性（即“喇叭口”或弯曲）或者在ANOVA表中出现了严重的失拟，就说明此时对于现在的响应变量拟合此线性方程是不合适的。对于残差图中出现了“喇叭口”通常需要对响应变量进行某种变换，这点容易理解，也容易找到含有数据的实际例题（这里不详细举例解释了），但有时明明看着残差图好像不正常，但又说不出哪里有问题。因此，凡是残差与响应变量预测值的残差图或残差与自变量的残差图出现弯曲（不用管ANOVA中弯曲项及失拟项是否显著），则通常需要检查残差是否齐性，并确定是否需要对于响应变量进行变换。至于“弯曲”与“失拟”两者的差别与联系，我们只能简单介绍一下。一般，我们在DOE中说的“弯曲”通常都是指响应变量的回归方程中未含二次项时，以中心点的试验结果与试验点连线形成的线性方程为比较标准，查看是否与线性回归方程有显著偏离；我们在DOE中说的“失拟”通常都是指响应变量的回归方程中未含各高阶项（三次、四次等）、高阶交互作用项时，试验结果是否与回归方程有显著偏离。由于二者强调的内容不同，常常出现只有“弯曲”及“失拟”中的某一项，对于它们的解决方法当然也是不同的，对“弯曲”常增加二阶项即可；对“失拟”则复杂得多，先要判断是缺什么项造成的，然后补加该项即可。有时，看起来像是有“弯曲”，但ANOVA中“弯曲”并不显著，而“失拟”倒很显著，这就要更仔细地分析才行。详细介绍见例13—7。

对于残差图中出现了“喇叭口”的情况我们不再举例（在例9—5氨损失量的回归分析中有类似的状况），下面举例说明因出现“失拟”而需要对响应变量进行变换的情况。

例13—7

提高金属疲劳寿命试验。为了提高钢板的性能，特别是担心钢板在长期使用后由于疲劳而发生断裂的情况出现，要选择最佳的材料、热处理工艺条件等。现在普遍使用电渣重熔钢方法冶炼，这里含2个重要因子要考虑：A（铬的含量）和B（锰的含量）。在热处理过程中，一般处理方法是相同的，可变的只有因子C：热处理时间。对于这3个因子安排含3次中心点的2水平全因子试验。A：铬的含量高水平为1.46％，低水平为1.42％；B：锰的含量高水平为0.32％，低水平为0.28％；C：热处理时间高水平为80分钟，低水平为60分钟。在疲劳寿命试验中在低温情况下用弯折机对钢板条进行反复弯折，以折断所需次数为响应变量寿命（单位：次数）。试验结果列在表13—11中（数据文件：DOE_疲劳寿命（变换）.MTW）。

表13—11　金属疲劳寿命试验数据

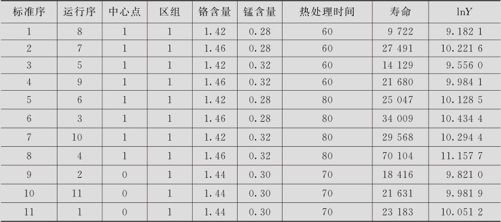
解　对于此数据的分析过程的操作与例13—4完全相同，但对于结果的分析则要仔细注意，特别要重视残差图与数值分析结果的对应解释。拟合模型的数值结果如下：

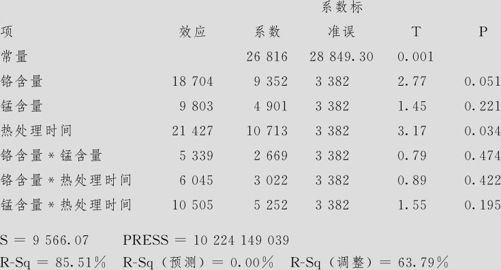
寿命的估计效应和系数（已编码单位）

寿命的方差分析（已编码单位）

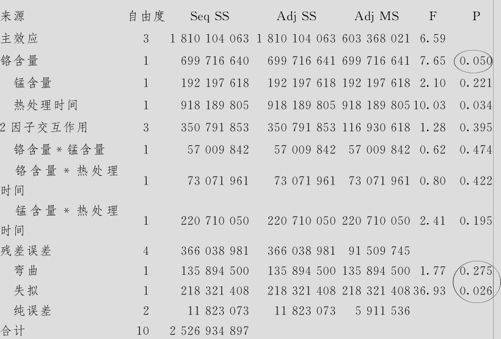
从上述结果可以看出，虽然模型总响应勉强是显著的，但这里出现了严重的失拟，可弯曲却又看不出问题。下面用残差图（见图13—35）来验证分析。

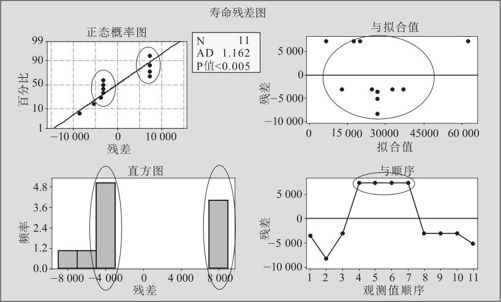
图13—35　提高金属疲劳寿命试验的四合一残差图

这个四合一残差图显得怪怪的，残差的数值好像集中在两处（见图13—35左上及左下）。再从对3个自变量的残差图（见图13—36中左上、右上及左下）可以看出明显的“弯曲”，可数值结果却只认为有“失拟”，而不认为有弯曲，所以还不能仅使用“增加自变量高阶项”的办法来解决。

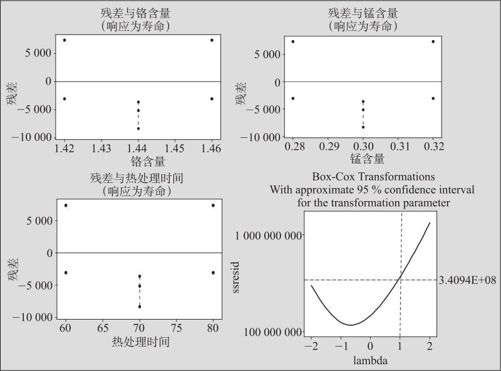
图13—36　疲劳寿命试验各个自变量的残差图及宏指令结果

为了处理含有失拟的这种问题，通常应该对模型拟合方面是否有大的问题予以检查，这通常与“是否需要对响应变量进行变换”结合起来。

为此，我们调用宏指令来观察是否需要和怎样进行对响应变量的变换。调用方法与例13—4完全相同。本例响应变量值存在C8列，设计矩阵存在并命名为M1，选取了变量共7个（3个自变量，3个交互作用项，1个常数项），故调用格式为：

％boxcoxdoe　C8　M1　7　C21-C60

结果得到图形如图13—36中右下图所示。

从图13—36中右下图可以看出，当λ＝1时，蓝线略微超过了红色的边界线，因而提示我们应该对响应变量进行变换。究竟λ选多少最合适？图中似乎认为λ＝－0.5最好，但考虑到实际意义，取负次方幂较难解释，况且λ＝0也是一个较好的选择，而λ＝0意味着对响应变量取对数，而这是很常见的手法（以后在“可靠性统计分析”可以知道，当寿命分布为Weibull分布等很多情况下都要取对数）。我们就在数据表中，另行生成一列lnY列（见表13－11第9列）。下面的工作就是对于lnY进行分析，当分析结束后，再将其数值取指数还原为寿命数据。

对于lnY进行分析的结果则一切正常了。残差正常，显著自变量只有A及C（即铬含量和热处理时间），当铬含量最高及热处理时间最长时，金属的疲劳寿命将达到最大。

13.3.4.4　带区组的试验设计及分析

我们在上面介绍的试验设计中，一般都暗含假定了在试验的整个过程中，一切条件都是不变的，换言之，所有的试验都是在有计划的安排之下，试验中只受到完全随机的试验误差干扰，试验条件的变化是根据设定的因子的变化而给定的，试验材料性能保持不变，人员保持不变等，我们概括地称之为试验条件是“齐性”的。但在实际工作中，时常会出现在随机干扰的同时，还有系统的干扰，例如材料并非由单个供应商提供，材质可能有不全相同的情况，不同的试验人员和试验工具等，即称为试验条件是“非齐性”的。如果不考虑这种非齐性的情况（例如材料在试验过程中有变化），则会使试验误差增大，在进行ANOVA分析及因子响应分析时，由于分母（误差项）变大，而常常不能敏锐地发现已经有显著效应的因子或交互作用。如果我们能事先明确造成非齐性的原因（例如试验中必须使用两批材料，将其作为区组），将这项原因分离出来，即有

这里把误差项分为“区组”部分和“剩余误差”两部分后，当有“区组”效应出现时，“剩余误差”部分将远小于原来的全部“误差”项。这时，对于总离差平方和的分解式写出示意关系是这样的。

未将区组列入模型：

将区组列入模型：

由于有这样的拆分，在进行ANOVA分析和各因子主效应（或交互效应）分析时，将大大减小分母的数值（由SS_误差换成SS_剩余误差），因而会敏锐地发现已经有显著效应的因子或交互作用，提高试验的精度。

有人会问：将全部试验安排在不同的区组内，实际上不也是将区组当成了一个因子了吗？是的，但它与普通的因子并不一样。虽然在试验安排或统计分析过程中，处理起来是都采用相同的按“因子”来处理，但一般来说，我们对研究因子的效应是感兴趣的，而对区组的效应是不感兴趣的。区组是客观存在的不得不面对的试验条件的不同，我们不必也不能将区组取消掉而让全部试验一定在齐性条件下进行。对于这种不得不考虑的因子，常常也称之为“讨厌因子”。

在对于含区组的试验设计的处理中主要是要注意：在分析时，区组一定要当作因子的分析（这样分析才能准确、灵敏）；在预报时，区组一定不要当作因子，在模型中应予以删除（能加以“设定”的因子通常已经是可控的普通因子了）。下面举例来说明带区组的试验设计计划安排及统计分析方法。

例13—8

陶粒混凝土强度的分析。一般的混凝土是由水泥、砂及石料所构成的，石料虽然坚固，但其自重过大，这是普通混凝土的最大缺点。发电厂在使用粉煤发电时，必然产生大量的粉煤灰，存放粉煤灰既占空间又容易污染环境，将粉煤灰经烧结而形成鸽蛋大小的球状物陶粒，不但能代替石料形成混凝土，而且将污染环境的粉煤灰清理干净，是一项有重大环保价值的举措。本试验设计为探索生产陶粒混凝土的工艺条件。为了提高陶粒混凝土构件板的强度，要选择最佳工艺条件，这里含4个重要因子：A水泥用量，B含砂率，C陶粒用量，D搅拌时间。全因子试验（含中心点）至少20次左右，而实际试验过程中，由于同炉生产的陶粒无法满足这样多试验的要求，只好使用由两个烧结炉烧结而成的共两批陶粒，同炉陶粒可以保证有较好的同质性，而两炉则不能保证它们的性能没有显著差别，考虑这样的安排就是把材料的不同来源当作区组，这就是含区组的试验设计。安排4因子的2水平全因子试验，分两个区组（甲、乙两炉陶粒），共含4次中心点。A：水泥用量，高水平为220kg，低水平为200kg。B：含砂率，高水平为38％，低水平为36％。C：陶粒用量，高水平为280kg，低水平为260kg。D：搅拌时间，高水平为8分钟，低水平为6分钟。区组1、2分别为甲、乙两炉生产的陶粒。试验结果列在表13—12中（数据文件：DOE_陶粒（含区组）.MTW）。希望分析出显著因子及显著交互作用项，给出在现有条件下的最优设置条件，并预报出在最优设置条件下强度的预测值及相应置信区间。

表13—12　陶粒混凝土强度试验数据表

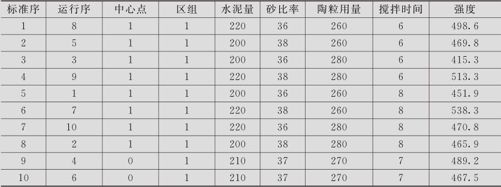
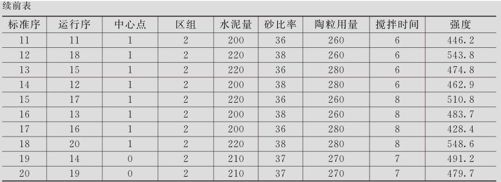
解　在生成试验计划时，填写因子个数时仍应填“4”（区组因子个数不计算在内），在“设计”中，选“每个区组含中心点数”为“2”，“仿行数”保留为“1”不变，“区组数”填写为“2”；打开“因子”项后，按要求填写4个可控因子的名字及相应高低水平之值，这就可以得到试验计划表了（见表13—12的前8列）。

按区组设计要求，两个区组各进行10次试验，养护28天后，将混凝土构件放在压力机上受压破碎，记录下其结果列在“强度”列中（见表13—12最后一列）。

在分析带区组的试验设计时要注意：分析时要将“区组”选为因子（因此因子个数要增加一个），中心点与原来一样仍然保留不选“在模型中包含中心点”项；在残差分析的图形中，对于“残差与变量”框，除了要填写各自变量外，要增加残差对“区组”的图形（操作图如图13—15中左下图所示，在最下方的“残差与变量”栏中，加选“区组”即可，此处界面从略）。

计算结果如下：

拟合因子：强度与区组，水泥量，砂比率，陶粒用量，搅拌时间

强度的估计效应和系数（已编码单位）

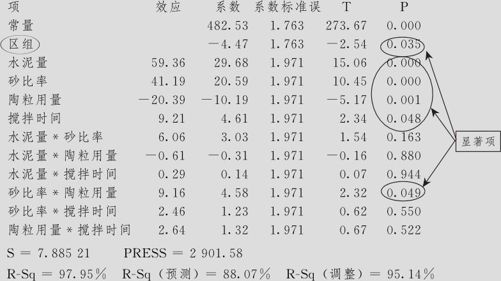
强度的方差分析（已编码单位）

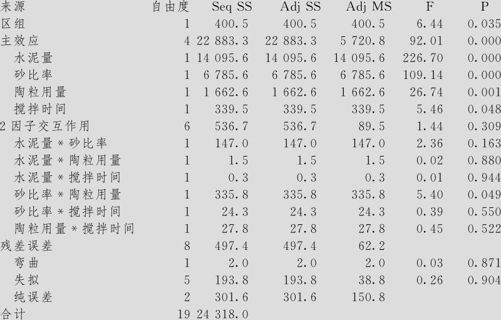
分析时，首先要看ANOVA中模型的总效果是否显著（本例的主效应项的p值为0.000，因此模型总效果显著），是否有“弯曲”或“失拟”（本例这两项p值分别为0.871和0.904，都不显著）。在此基础上，容易看出，区组效应项的p值为0.035，说明区组的效应还是显著的（即两炉生产的陶粒间确实有显著差异，我们原来的担心被证实了）。本例中，残差分析都正常（从略），显著项（以α＝0.05为显著水平）有全部4个主效应项及交互作用项“砂比率*陶粒用量”。

由于残差图都正常，修改模型只需删除不显著项，其结果如下：

拟合因子：强度与区组，水泥量，砂比率，陶粒用量，搅拌时间

强度的估计效应和系数（已编码单位）

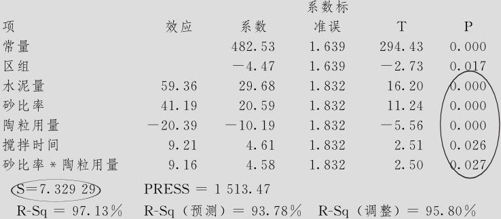
强度的方差分析（已编码单位）

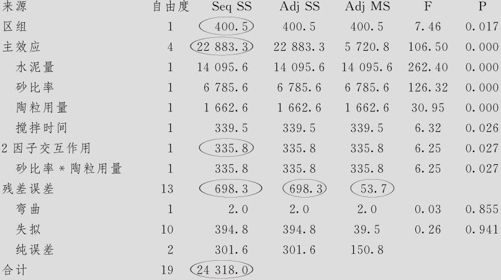
写出完整的回归方程为：

回归方程中各自变量上带有“*”是表示代码化的数据，回归方程对于区组是分叉给出的。

下面求出在现有条件下的最优设置条件，并求出在最优设置条件下强度的预测值及相应置信区间。

由上述回归系数的估计结果，加上因子效应图及等值线图等工具的使用，可以看出在现有条件下的最优设置条件是：水泥量、砂比率及搅拌时间取高水平（水泥量＝220kg，砂比率＝38％，搅拌时间＝8分钟），陶粒用量取低水平（陶粒用量＝260kg）将会使构件强度达到最大。由于我们对于最佳设置的选择应该与区组无关（因为预报时事先无法选择或指定某个区组），因此进行预报时必须按上述显著项对于不含区组的模型重新计算，然后才能代入求出预测值及相应置信区间。我们先对不含区组的模型进行计算，其结果为：

拟合因子：强度与水泥量，砂比率，陶粒用量，搅拌时间

强度的估计效应和系数（已编码单位）

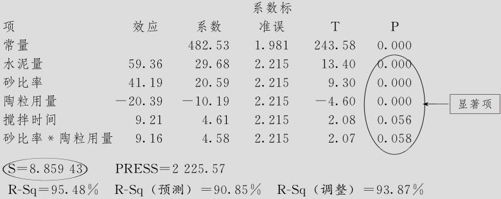
强度的方差分析（已编码单位）

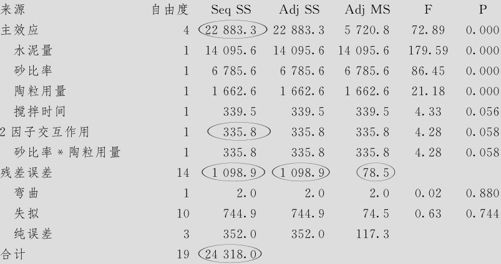
比较一下“将区组列入模型”和“未将区组列入模型”，可以看出它们的差别。两者的总离差平方和虽然都是24318.0，将区组列入模型时，分解式为：

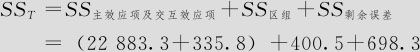
未将区组列入模型时，分解式为：

但正因为区组效应显著，原来分母误差项离差平方和中将分离出有很大的数值的区组离差平方和（总SS_误差＝1098.9，扣除SS_区组＝400.5），剩余的参加效应分析的分母将变得小很多（本例中SS_剩余误差＝698.3），这使各个系数的显著性估计都更准确了。总之，将区组列入模型会把SS_误差（1098.9）换成SS_剩余误差（698.3），确实会使各个因子效应项及回归系数的估计精度提高。

实际上也确实如此：将区组列入模型的分析中，4个主因子及交互作用项“砂比率陶粒用量”都是显著的；但未将区组列入模型的分析中，因子D（搅拌时间）及交互作用项“砂比率陶粒用量”都变成不显著的了。我们的分析结论必须以将区组列入模型的分析为准。但进行结果预测时，我们一定要用“未将区组列入模型”的回归结果来计算，但最佳设置一定要按“将区组列入模型”的回归结果来给出，在删除不显著的5个交互作用项后，再将4个自变量的设置都代入。事实上，将区组列入模型的分析中对于标准差的估计量是S＝7.32929（这是MS_剩余误差＝53.7的平方根），未将区组列入模型的分析中对于标准差的估计量是S＝8.85943（这是MS_剩余误差＝78.5的平方根），我们的预测必须以较大的标准差作为预测值波动的基础。本例得到的计算结果是：

我们得到的陶粒混凝土构件强度的预测值为543.029，其多次试验的平均值的95％置信区间（称为95％置信区间CI）为（531.588，554.469），其单次试验的值的95％置信区间（称为95％预测区间PI）为（520.849，565.209）。

这里要说明的是，如果试验结果的分析中指明“区组效应显著”的话，应该引起警惕。为什么会出现这样的显著差异？要尽量分析出原因，以便对误差加以控制；实在找不出原因时，只能承认试验误差太大，要对预测结果可能存在的较大波动进行充分的估计。

13.3.4.5　离散型响应变量的试验设计及分析

我们在上面介绍的所有的试验设计中，全都假定了响应变量是取连续型数值的。但在实际工作中常常会遇到离散型响应变量的情况，主要是收集到的数据是只有“是”“否”、“合格”“不合格”的计量型结果，计算出来只有合格率、不良率等类指标。这时一定不要勉强将合格率、不良率数据当作连续型变量来处理。有人认为，比率是带小数的，当作连续型变量来对待在外表上是看不出问题的。但实际上除非样本量很大（达到成千上万），否则都是有很大问题的。

回顾在Logistic回归中讨论的问题，那时就是要处理响应变量是离散型数值时的处理办法，现在的问题是相同的。仿照Logistic回归的办法，处理离散型响应变量的最好办法是对这些数据采用变换的方法，化成连续型变量来处理，最常用的变换是Logistic变换。关于Logistic变换的基本内容，我们已经在本书9.4节“离散变量Logistic回归”中，做了介绍。在式（9—33）中，给出了下列公式（下面重新给出并给出新公式号），它可以将比率p变换成连续型数据y：

式中，p是“成功”比率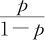，称为差异比（odds ratio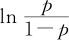），称为是比率的Lo-gistic变换。在得到y值后，可以将式（13－22）反解求出p，得到下式：

现在再补充说明一些在试验设计中对于式（13—22）的应用方法。

通常，如果进行了n次试验，其中“成功”（注意，“成功”可能代表着“良品”，也可能代表“不良品”）为x次，一般都是用式（13—24）作为p的估计量：

大家公认这样的估计是天经地义的，但如果用此值作为响应变量来进行试验结果的分析理论上是不妥的，而且估计出的结果也不准确。在一般情况下，当x不小于5，n不小于100，这样估计是可行的。但在式（13—24）中，如果出现x＝0或x＝n的情况，p将估计为0或1，这时带入式（13—22）无法取对数，因此，式（13—24）就有问题了。另外，用式（13—24）估计得出的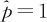或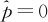在解释上也不一定合理。例如，1976年，唐山大地震后，要对京津地区的地震烈度进行测定（注意，一个地震的震级只有一个，唐山地震的震级为7.8，但各地区的烈度可以是不同的。例如，唐山市区的地震烈度为11度；天津烈度大部分是8度，局部地区为9度；北京则更小些）。调查烈度的粗略方法是将某指定地区划分为0.5千米见方的小方格，在每个小方格内，现场计数高度超过8m的烟囱总数及倒塌数，以倒塌比率来估计该小方格区域的地震烈度，这样的粗略估计是有效的。但是，如果一个小方格内有3个烟囱，全部倒塌；另一个小方格有100个烟囱，也全部倒塌；这两个小方格区域倒塌率估计值皆为1，可是后者的烈度肯定会更强些，因此用式（13—24）作为p的估计量似乎不够合理。经过统计学家使用Bayes理论的分析，在假定p的先验分布在［0，1］是上均匀分布时，得到p的Bayes估计为：

工程界结合工程经验，将式（13—25）修正为式（13—26），这个公式已纳入多项国际标准及国家标准。

我们也推荐这个公式。以此式为依据，则式（13—22）将写成：

总之，如果进行n次试验，其中“成功”次数为x，将这两个数值代入式（13—27），得到y值，我们就可以将y值当成连续型响应变量进行各项统计分析了。下面举例给出详细的计算步骤并说明用x/n来估计不良率之缺点。

例13—9

降低TPU单板不良率的试验分析。将合格的芯片颗粒进行封装并焊线、点胶后用模压将其成型，再用高温封装。初步分析认为，焊线时焊机使用的时间，模压时的压力及最后高温封装时的温度是影响单板不良率的3个显著因子。为降低最后的不良率，进行了3因子各2水平加4个中心点的全因子试验。因子A：焊机使用时间，高水平为80毫秒，低水平为60毫秒；因子B：模压时的压力，高水平为260帕，低水平为240帕；因子C：高温封装温度，高水平为160℃，低水平为150℃。安排全因子试验设计，再安排4个中心点作为试验误差的估计。试验结果列在表13—13中（数据文件：DOE_单板不良率（离散响应）.MTW），其中记录了试验件数n和不良件数x。希望分析出显著因子及显著交互作用项，给出在现有条件下的最优设置条件，并预报出在最优设置条件下不良率的预测值及相应置信区间。

表13—13　TPU单板不良率的试验数据表

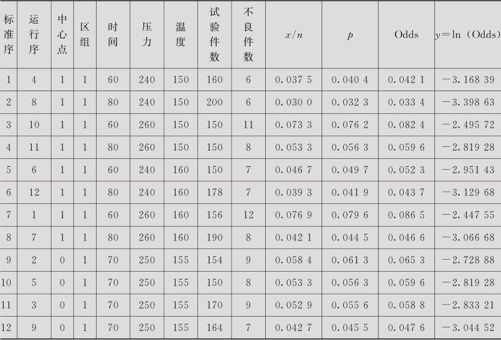
解　这是典型的离散型响应变量的例子。我们列出x/n的值（见表13—13的第10列），用式（13—25）来估计不良率p值（见表13—13的第11列p），用式（13—25）来估计出差异比（见表13—13的第12列Odds）及比率的Logistic变换值（见表13—13的第13列即最后一列y）。下面的分析就以y为响应变量。所有操作与例13—4完全相同，我们只摘录出一些重要结果，详细内容从略。

初步分析结果说明，模型的拟合效果是显著的，残差是正常的，显著的因子只有A（焊机使用时间）和因子B（模压时的压力）。修改模型时，对于将比率经Logistic变换转为连续变量者不能再次考虑是否要再进行Box-Cox变换了，修改模型只需将不显著的各项删除就行了。现在将不显著的交互作用项删去，就可得到最终的模型。经分析，A（焊机使用时间）取最大值（80毫秒）且因子B（模压时的压力）取最大值（240帕）时不良率将达到最小。其预测结果如下：

根据该模型在新设计点处对y＝ln（Odds）的预测响应

新观测值的自变量值

这是式（13—22）中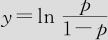中的y值的计算结果，我们用其反变换式（13—23）得到不良率p的预测值及其CI见表13—14。

表13—14　单板不良率的预测结果表

可以看出，最佳设置将使TPU单板不良率降为约3.54％，95％的置信区间CI为（2.9％，4.2％），95％的预测区间PI为（2.4％，5.1％）。

表面上看，如果不考虑离散型数据的背景，直接以x/n计算p，再求出yy＝ln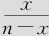，然后对yy进行分析是否可行呢？回答是否定的。从理论上讲，我们的试验设计的分析工作都是对结果进行回归分析而得到的，而回归分析是需要很多条件的（3条假定的详细内容请见第9章的9.2.1节），这里关键的是第2条“当自变量x取某特定值时，对应的y值服从正态分布，且这些正态分布对于不同的自变量x值是等方差的”，对于p的估计值x/n而言，显然不能满足这一条件，特别是当试验次数越少时或p越接近于0或1时偏离正态就越严重，而且方差的波动越大。这样一来，回归分析不能使用，DOE的分析结果当然也是不可信的了。

根据该模型在新设计点处对yy＝ln（x/（n－x））的预测响应

在本例中，不良率大约3％～8％，还不算非常小，用x/n勉强来计算，得到的不良率p的计算结果已经发现偏小了（相应计算结果列在表13－14的最后一列中供参考），当不良率p变得更小（或接近于1）或试验次数减少时，则预测值甚至可能差10倍以上，用x/n来计算是不可取的。