3.2　描述性统计

收集和罗列数据是统计资料处理的初级阶段，日渐庞大的原始数据资料往往会使人无所适从，进一步的研究分析不仅要求我们对数据分布变化有直观的了解，而且要求我们能用几个既简洁又有效的统计量将其分布变化的规律性表示出来。描述性统计就是与这个问题相关的统计学工具，力求能够高度综合地概括出数据中所蕴含的关于总体的统计特征。在第2章中，我们介绍了总体相应各参数的含义，包括位置状况、离散程度和分布形状等的度量，但这些参数在获得样本后如何用相应的统计量来代表呢？本节将逐一介绍几个最常用、最重要的指标。

3.2.1　位置状况

在大多数情况下，较大或较小值发生的频数一般比较少，大部分数值总是集中在某个区域内不断变化，使总体大体上落入某个范围内，这就是所谓的数据位置状况的问题，这是人们最关心的一类数据特征。比如，零件的平均长度、焊锡膏的平均重量、员工的平均工资，等等。度量数据位置状况的指标主要有平均值、中位数和众数等。

3.2.1.1　平均值

样本平均值（常简称样本均值，sample mean）是最常用来表示数据的位置状况的，它反映随机变量各个取值的中心位置或均衡点。总体的均值相当于分布密度重心的横坐标，样本均值则是将所有数据的数值相加，除以数据的个数即可得到，即

平均值具备良好的数学特性，因此无论是在描述统计学，还是在后文介绍的推论统计学中，它的应用都非常广泛。例如3，2，1，7，4的平均值是（3＋2＋1＋7＋4）/5＝3.4。

3.2.1.2　中位数

样本中位数（sample median）是反映数据位置状况的另一个常用统计量。总体的中位数相当于面积位于50％处的横坐标，样本中位数则是将所有数据按从小到大的顺序进行排列，位置居中者的数值。当数据的个数为奇数时，居中的数值直接就是中位数；当数据的个数为偶数时，居中的两个数值的平均值就是中位数，即

式（3—2）中带括号的下标表示样本排好顺序后的样本值，X_（i）代表排序后左起第i个样本的值。如果数据为2，8，5，1，6，则其中位数是5，而2，8，5，1，6，10的中位数是（5＋6）/2＝5.5。

当分布基本上对称时，样本平均值与样本中位数应该相差不多；但有较严重的偏斜或数据中含有异常观测值时二者会有较大差别，这时，应该说中位数对于位置状况有更好的代表性。这种对异常观测值反应不敏感的特性，称为稳健性（robust）。因此可以说，在度量位置状况时，中位数比平均值对于异常值更稳健。

3.2.1.3　众数

众数（samplemode）是指数据中出现最频繁的那个数值。从这点来看，众数也可以用来描述数据的位置状况。但是众数的存在有可能并不唯一。例如1，1，2，3，4，4，4，5中的众数是4，而1，2，3，4，5，6，7，8中每个数都是众数。相对其他位置参数的度量，众数的代表性要差很多，甚至在总体中也是这样。众数虽然也可以有意义，但用得很少。

3.2.1.4　第一四分位数

第一四分位数（sample 1^st quartile，Q1或LQ）是这样一个数，当把数据集划分为两个部分时，其中小于等于此数的数据约占整个数据集的25％，大于等于此数的数据约占整个数据集的75％。它的准确计算公式是：首先将样本按从小到大的顺序排好，记其中第i名者为X_（i）。对于给定的n，先求出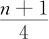，其整数部分记为k，其小数部分记为f（当然0≤f＜1）。

例如，n＝40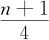，＝10.25，k＝10，f＝0.25，所以Q1一定介于X_（10）与X_（11）之间，而且有Q1＝X_（10）＋0.25（X_（11）－X_（10））。样本量较大时，临近次序统计量间的差距很小，可以取f＝0.5，因而可以近似有

式中，k是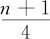的整数部分。

3.2.1.5　第三四分位数

第三四分位数（sample 3^rd quartile，Q3或UQ）是这样一个数，当把数据集划分为两个部分时，其中小于等于此数的数据约占整个数据集的75％，大于等于此数的数据约占整个数据集的25％。它的准确计算公式是这样的：对于给定的n，先求出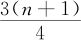，其整数部分记为k，其小数部分记为f（当然0≤f＜1）。

例如，n＝40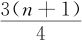，＝30.75，k＝30，f＝0.75，所以Q3一定介于X_（30）与X_（31）之间，而且有Q3＝X_（30）＋0.75（X_（31）－X_（30））。样本量较大时，临近次序统计量间差距很小，可以取f＝0.5，因而可以近似有

式中，k是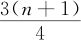的整数部分。

3.2.2　离散程度

只用位置状况的指标来描述数据是不充分的，甚至会产生误解。例如A，B两个城市居民的人均住房面积均为18平方米，此时我们的直觉是这两个城市的居民住房生活水平差不多。可事实上，A城市居民的人均住房面积最高达80平方米，最低只有5平方米。而B城市居民的人均住房面积最高为40平方米，最低为10平方米。显然，A城市居民住房面积的离散程度远大于B城市。如果忽略考虑数据的离散程度，就可能导致错误的判断。统计学的一个重要原则就是“不简单地相信平均值”，因为必须同时考虑离散程度。度量数据离散程度的指标主要有方差、标准差和极差等。

3.2.2.1　方差

方差（variance）的应用十分广泛，总体的方差相当于密度分布围绕重心的转动惯量，对于样本方差则是将所有数值减去平均值，加以平方，然后求出差值平方的平均值，就可得到方差，即

与总体参数的含义相同，样本方差值越大，表明数据间的离散程度越大；方差值越小，表明数据间的离散程度越小。例如一组样本的数值分别是3，2，4，5，1，其样本均值是3，则其样本方差S²可计算如下：

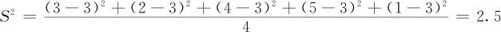
3.2.2.2　标准差

将方差开算术平方根即可得到标准差（standard deviation），即

方差的计量单位是原始数据的计量单位的平方，但标准差的计量单位则与原始数据的计量单位完全一致，所以很多人更习惯使用这个指标描述数据的离散程度。但在很多方面方差也有很多优点是标准差所不能替代的，最主要的就是方差具有可加性，而标准差则没有。例如，一个制造过程，过程的总方差可以分解为若干部分方差的和（详细内容参看本书第10、11两章）；标准差则不能这样分解。“六西格玛管理”名称中的“西格玛”也来源于标准差。上例数据的标准差直接计算就是2.5的算术平方根，即。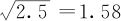

3.2.2.3　极差

极差（range）也称全距，是指一组数据中的最大值与最小值之间的差值，即

极差计算方便，意义明显，但由于它仅仅取决于一组数据中的两个值，存在一定的局限性，一般只能粗略地反映数据的离散程度。例如4，6，9，1，5的极差是9－1＝8。它只在样本量较小时使用（通常不超过6，绝不能大于10）。在总体参数中，一般不列出此参数，因为相当多的分布两侧或单侧是无限的，根本不存在“极差”的概念。极差是统计量中所特有的。

3.2.2.4　四分位间距

四分位间距（interquartile range，IQR）等于第三四分位数与第一四分位数的差值，即

它代表了居中的50％数据范围的宽度。与总体参数的含义相同，样本四分位间距越大，表明数据间的离散程度越大；四分位间距越小，表明数据间的离散程度越小。

以上四个描述离散状况的统计量各有优劣。总的来说，标准差最为常用，它对离散状况有较好的代表性；另外，它与样本量关系不密切，样本量大些或小些都可以使用，n大于6时标准差要比极差好些，但标准差的缺点是对异常值敏感。方差与标准差相似，方差的量纲虽为原量纲的平方因而不太方便，但有时它具有的可加性很方便。极差与样本量关系十分密切，对异常值也很敏感；但它计算简单，当n较小时代表性已足够。四分位间距与样本量关系不密切，且对异常值不敏感，是所有离散状况度量的统计量中最稳健的。

3.2.3　分布形状

只用反映位置状况和离散程度的指标表示所有的数据，仍然不够完善。如果能增加反映数据分布形状的指标配合前两者，将更能完整地呈现数据的特性。偏度和峰度是最常用的两个度量数据分布形状的指标。

3.2.3.1　偏度

偏度（skewness）是对数据不对称性的度量，总体参数偏度用β_s表示，样本统计量偏度用b_s代表。计算公式为：

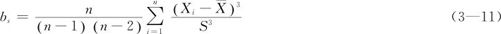
为了直观理解，我们曾画出过不同偏度的总体的图形（见图2—15），下面给出不同偏度的抽样结果的分布直方图（见图3—1）。与总体的参数性质完全一样：当分布完全对称时，b_s应该近似为0（见图3—1（b））；b_s为正数，代表分布有正偏度，表示分布高于均值的“右尾”部延伸严重（见图3—1（c））；b_s为负数，代表分布有负偏度，表示分布低于均值的“左尾”部延伸严重（见图3—1（a））。

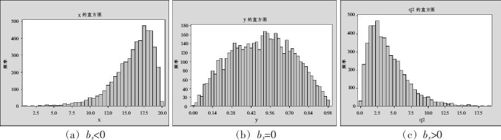
图3—1　样本偏度示意图

3.2.3.2　峰度

峰度（kurtosis）是数据分布平坦性的度量，总体参数峰度用β_k来表示，样本统计量峰度用b_k代表。计算公式为：

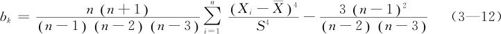
为了直观理解，我们画出过不同峰度的总体图形（见图2—16），下面给出不同峰度抽样结果的分布直方图（见图3—2）。与总体的参数性质完全一样：正态分布的峰度为0；峰度为正数时，表示数据分布比正态分布顶峰更峭、两尾更重（见图3—2（b））；峰度为负数时，表示数据分布比正态分布顶峰更平、两尾更轻（见图3—2（a））。负峰度常来自均匀型分布或多个不同均值的正态分布的混合。两图中的参考曲线都为具有同样均值及同样方差的正态分布（峰度为0）。

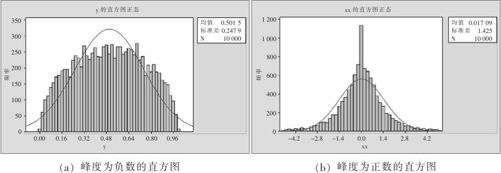
图3—2　样本峰度示意图

下面用一个案例综合展示上述指标的实际应用。

例3—2

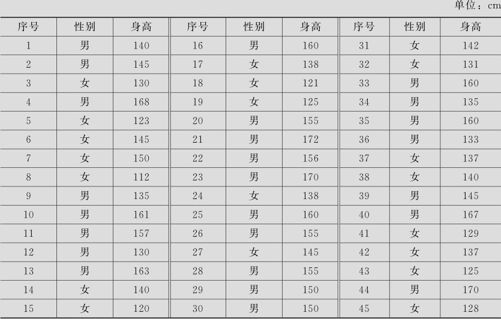
为了解育才小学学生的身体素质状况，对该校的小学生进行随机抽样，并测量了其性别与身高，试对此做描述性统计分析（数据列在表3—1中，数据文件：BS_描述性统计.MTW）。

表3—1　学生身高数据表

解　运用计算公式可以逐一手工计算获得描述数据的位置状况、离散程度和分布形状等各项指标。这里介绍一个使用MINITAB的相关命令进行描述性统计计算的简便方法。

（1）选择“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”。

（2）指定“变量（Variables）”为“身高”，则可得到如图3—3所示的图形输出。

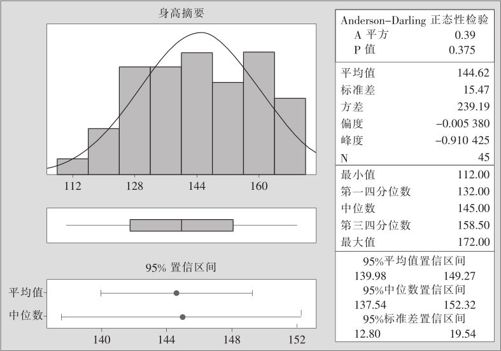
图3—3　学生身高的统计分析

从图3—3中可以直接看到多个反映数据特征的指标：

1）位置状况：

样本平均值＝144.62cm

样本中位数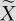＝145.00cm

第一四分位数Q1＝132.00cm

第三四分位数Q3＝158.50cm

2）离散程度：

样本方差S²＝239.19cm²

样本标准差S＝15.47cm

3）分布形状：

样本偏度bs＝-0.005380（几乎为0，基本对称）

样本峰度bk＝-0.910425

峰度为负，很可能是因男女生两个不同总体的混合造成的。