9.5　广义回归

在实际问题需要进行回归分析时，自变量中不仅会有连续变量，也会有离散变量，更多的情况是同时遇到这两类变量。本节就介绍同时遇到这两类变量的回归分析问题。准确说来，离散变量应当称为“类别变量”（categorical variable），每个“类别变量”的值只能取有限个，而且值间不能做算术运算。如果事先能够确认响应变量与连续自变量间的函数关系，当类别变量取不同值，我们必须选用相同的函数关系，但其回归系数可能有不同。以下讨论两种情况：如果当类别变量取不同值，函数关系中只有截距项不同，我们称此类别变量与连续自变量间没有交互作用；如果当类别变量取不同值，函数关系中回归系数有不同时，我们称此类别变量与连续自变量间有交互作用。一般情况下，我们不能事先断定二者是否有交互作用，在进行回归分析的过程中可以检验回归系数以确定交互作用是否存在。

广义回归分析的应用非常广泛。比如有两家实验室分析同一套试样，分别得到各自的回归方程，如何比较两个回归方程是否有显著差异？有几种工艺方法生产同种产品，其产品的性能是用某个回归方程来体现的（例如反应曲线），如何比较它们的差异？这些回归方程如果没有显著差异，我们就可以把这些数据合并起来，形成一个更精确的（因为样本量增加了）公共的回归方程；如果有显著差异，我们就要分清条件，分别使用适合于各自特点的不同的回归方程。下面我们通过两个例题说明此类问题的解题方法。

例9—11

儿童发育问题。幼儿（2岁至7岁）的身高随年龄的增长而增高，在A，B两省对各个年龄的幼儿分别抽取3名儿童，测量他们的身高（单位：厘米），其数据列在表9—16中（数据文件：REG_幼儿身高.MTW）。试比较两省间幼儿发育状况是否有显著差异。

表9—16　幼儿身高数据表

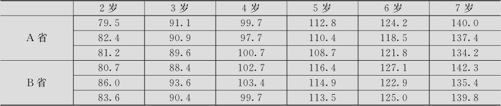
解　本问题中有两个自变量，一个是年龄（连续型），另一个是省份（类别变量）。下面先绘制散点图以观察变化规律。散点图见图9—38。

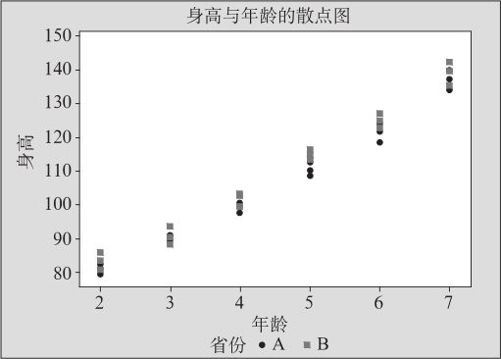
图9—38　幼儿身高增长散点图

从图9—38中可以看到，在幼儿阶段，身高与年龄的关系虽大体上是线性的，但不能排除有高阶项；两省间似乎差别也不大。但这些还应该仔细分析。本例是广义回归中最简单的情况：连续型自变量及类别变量自变量都只有一个。

首先不考虑年龄的二次项，也不考虑年龄与省份间的交互作用（方案1），此时这个类别变量“省份”只是当作一个单独的自变量，同时出现在“模型项”中及“类别变量项”中。其操作如下：

选择指令“统计＞回归＞广义回归（Stat＞Regression＞General Regression）”，得出界面如图9—39左上角所示。在“模型”中填写“省份　年龄”（注意，类别变量应该列入），在“类别预测变量”中填写“省份”；再点击“图形（Graphs）”，勾选“四合一（Four in One）”，在“残差与变量（Residuals Versus the variables）”中输入自变量名称，见图9—39中左下角。再点击“存储（Storage）”，勾选“残差（Residual）”及“标准化残差（Standardized Residuals）”，见图9—39中右下角。在“选项（Options）”中（见图9—39中右上角），将“类别预测变量的编码类型”由“（-1，0，+1）”换成“（1，0）”。计算结果如下（方案1）：

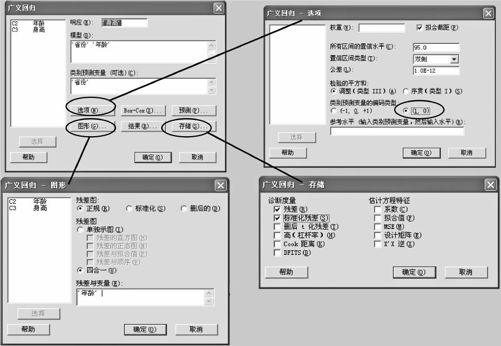
图9—39　广义回归操作图

结果：REG_幼儿身高.MTW

广义回归分析：身高与年龄，省份

回归方程

模型汇总

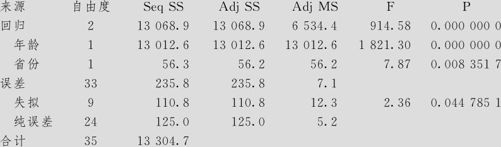
方差分析

异常观测值的拟合和诊断

R表示此观测值含有大的标准化残差

这里的方程按省份的不同分为两个回归方程，它们对于年龄的回归系数是相同的（都是11.1324），差别只反映在常数项上。计算方法是这样的：在回归系数列表中，常数项对于类别变量中的某个“参考值”（通常是按编码顺序位于最前者，本例为A省）默认的56.6154，在省份换为B时，此值应加上2.5000，因而得到其常数项为56.6154＋2.5000＝59.1154。

注：如果我们在“选项（Options）”中（见图9—39右上角），将“类别预测变量的编码类型”保留“（-1，0，+1）”形式时，计算机输出结果将是这样的：

这时，它们在常数项上的计算方法是这样的：在常数项上，公共值（加权平均值）为57.8654，在省份为A时，应加上-1.2500，因而得到其常数项为57.8654－1.2500＝56.6154；在省份为B时，应减去-1.2500，因而得到其常数项为57.8654＋1.2500＝59.1154。这种计算方法在类别数据只取两值时（即离散情况只分两种时），表达方式和计算难度与用“（1，0）”几乎是相同的；但如果类别数据取值超过两个时（即离散情况至少分三种以上情况时），在“类别预测变量的编码类型”的选择上，用“（-1，0，+1）”远不如换成“（1，0）”好。因此我们建议以后不论类别数据取值是多少，一律换成“（1，0）”，这样表达清晰且计算简单。

在本例输出的结果中，在ANOVA项中，整个模型是高度显著的（回归项的p值为0.000），但失拟项的p值为0.0447851，这样显著的失拟来自何处？从残差对于自变量的图形（见图9—40中左侧），数据点明显是有弯曲的。

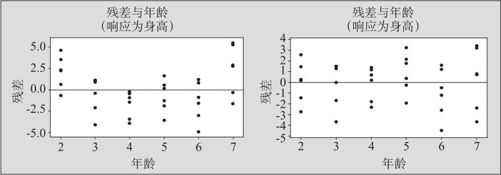
图9—40　幼儿身高对于年龄的残差图

这说明需要改进模型，应该增加对于自变量的二次项“年龄*年龄”（方案2），而广义回归中，增加这种项不需要另加一列给出计算值来，而只需在模型选项中增加填写此项即可。其操作图见图9—41中左侧。

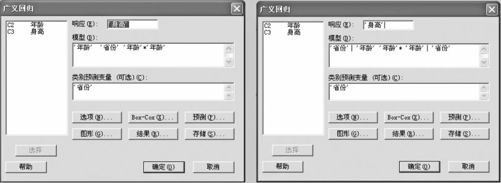
图9—41　幼儿身高对于年龄的模型填写图

这时的计算结果如下（方案2）：

回归方程

模型汇总

方差分析

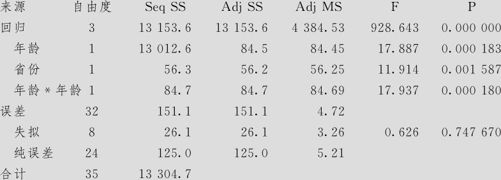
异常观测值的拟合和诊断

R表示此观测值含有大的标准化残差

这时的计算结果显示，我们的回归方程对于两个省份分别给出，对于身高与年龄的回归方程是二次的。ANOVA显示，回归总效果显著，没有失拟；年龄项及年龄平方项是显著的，两省间差异也是显著的（体现在回归方程中，回归方程中的截距项是显著不同的）。各个残差图也都显示正常，特别是残差对于年龄的图（见图9—40中右侧），是完全正常的。

但我们必须讨论下列问题：两省间的差异是否不仅表现在截距差别，而且是有可能二者的回归系数已经有差别？对此我们要给出明确的回答。这时就一定要引入交互作用项，并且在计算后确认，两组回归方程的回归系数是否有显著差别。

计算含交互作用的模型只需要修改“广义回归”的填写内容。这时模型项中应该包含“省份”、“年龄”及“年龄省份”三项，MINITAB软件将这种交互作用项简化写为“年龄|省份”。由于已知年龄的平方项肯定是显著的，因此应该将模型中改为“年龄|省份年龄年龄|省份”（见图9—41中右侧），这就是方案3。填写含交互作用项的一般准则应该是将类别变量放在竖线之后，但如果只有两项，例如“年龄|省份”和“省份|年龄”则顺序就无所谓了。其计算结果如下：

广义回归分析：身高与年龄，省份（方案3）

回归方程

系数

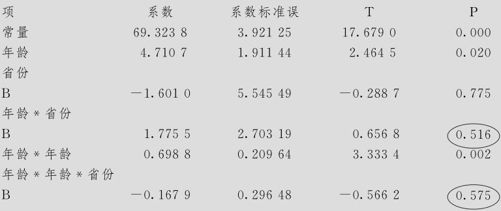
模型汇总

方差分析

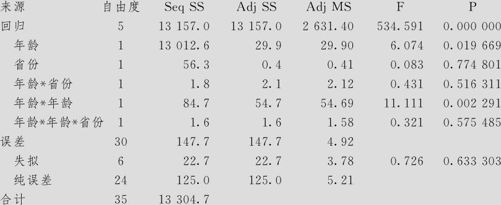
异常观测值的拟合和诊断

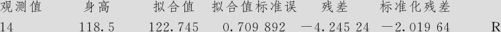
R表示此观测值含有大的标准化残差

在上述回归方程中，对于两个省份的回归方程是完全不同的。我们需要从结果中判断，这个交互作用效应显著吗？在“年龄省份”项中，B与A的差别之p值为0.516，说明交互作用不显著，在“年龄年龄*省份”项中，B与A的差别之p值为0.575，说明交互作用同样不显著。这就说明，两个省份间在回归方程的系数上没有显著差别，两省可以使用只是常数项不同而回归系数相同的方程，换言之，方案2的计算结果就是我们的最终结果，方案3的结果徒然变得复杂，它没有任何意义。

我们回到方案2的计算结果。如果我们需要预测A省6岁幼童平均身高情况，这时要再次从指令“统计＞回归＞广义回归（Stat＞Regression＞General Regression）”入口，得出界面（如图9—39中左上角所示）后，选择“预测”项，分别填写连续自变量及类别自变量的值（如图9—42所示）。这时要注意，填写类别变量省份A时，要在A前后加上双引号（要用英文半角字形）。

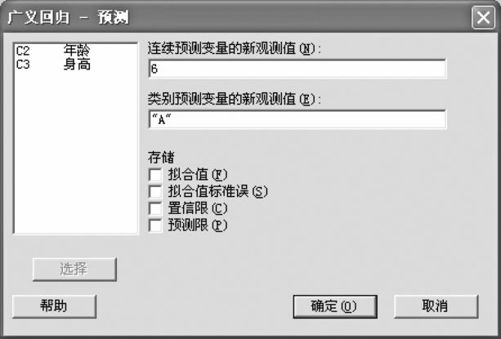
图9—42　广义回归的预测值计算界面图

计算结果如下：

新观测值的预测值

新观测值的自变量值

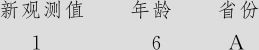
对于这些结果的解释与一般的回归分析中的预测是相同的，这里的“点预测”（就是将自变量值代入回归方程后计算结果）为123厘米，95％置信区间（即A省所有的6岁幼儿的平均身高）的95％置信区间为（121.756，124.244），95％预测区间（即A省一个6岁幼儿的身高的95％置信区间）为（118.402，127.597）。

下面再举一例，介绍类别数据取值在3个以上的情况，这时的计算要复杂一些。

例9—12

钢材锈蚀量的计算。为了降低钢材锈蚀量，我们希望对于钢材锈蚀的规律进行定量分析。钢材锈蚀不但与钢材配方有关（铬、镍含量越高则越不易锈蚀，当铬含量超过14％时则称之为“不锈钢”），而且与环境中的含盐量有关（盐越多锈蚀越快），与温度有关（温度越高锈蚀越快），与时间有关（时间越长锈蚀越严重）。现在的研究处于初期摸索阶段，希望先研究锈蚀与温度间的关系。我们将3种配方A，B及C（后两种增加了不同的铬及镍）生产出的不同之螺纹钢，直径都取Φ28，每种螺纹钢都再分为两组，选定30℃，50℃，70℃，80℃及90℃共5种温度，将螺纹钢都放入5％浓度的食盐溶液制成的盐雾箱中72小时，螺纹钢将被锈蚀。将原重量减去酸洗后剩余的重量即得到锈蚀量（单位：克）。我们希望建立锈蚀量Y与温度及配方间的回归方程。数据列在表9—17中（数据文件：REG_锈蚀量.MTW）。

表9—17　螺纹钢锈蚀量数据表

解　本问题中有两个自变量，一个是温度（连续型），另一个是配方（类别变量，取3个值）。下面先绘制散点图以观察变化规律。散点图见图9—43。

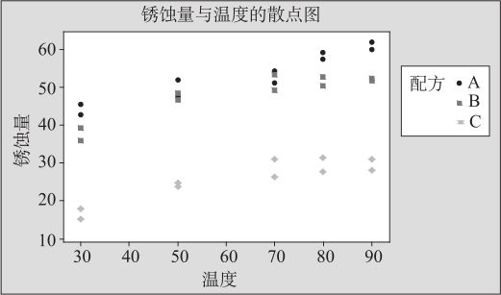
图9—43　锈蚀量与温度的散点图

从图9—43中可以看到，锈蚀量与温度的关系明显不能认为是线性的，因此考虑直接建立二次函数关系，即要包含温度的平方项。

首先不考虑含配方与温度间的交互作用（方案1），此时这个类别变量“配方”只是当作一个单独的自变量，同时出现在“模型项”中及“类别变量项”中。其操作与例9—10完全相同，这里只给出主操作窗（见图9—44），其他界面图从略。

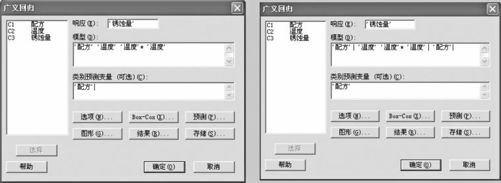
图9—44　广义回归操作图

选择指令“统计＞回归＞广义回归（Stat＞Regression＞General Regression）”，得出界面如图9—44中左侧所示。在“模型”中填写“配方　温度　温度*温度”（注意，类别变量应该列入），在“类别预测变量”中填写“配方”。点击“图形（Graphs）”后，勾选“四合一（Four in One）”，在“残差与变量（Residuals Versus the Variables）”中输入自变量名称，见图9—39中左下角。再点击“存储（Storage）”，勾选“残差（Residual）”及“标准化残差（Standardized Residuals）”，见图9—39中右下角。在“选项（Options）”中（见图9—39中右上角），将“类别预测变量的编码类型”由“（-1，0，-1）”换成“（1，0）”。

这时计算结果如下（方案1）：

广义回归分析：锈蚀量与温度，配方

回归方程

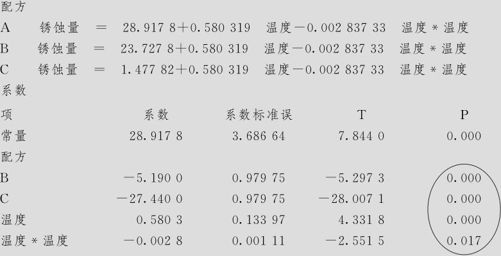
模型汇总

方差分析

异常观测值的拟合和诊断

R表示此观测值含有大的标准化残差

这时的方程按配方的不同分为3个回归方程，他们对于温度项及温度的平方项的回归系数是完全相同的，其差别只反映在常数项上。其计算方法是这样的：在回归系数列表中，参考值A的常数项为28.9178（通常是按编码顺序位于最前者，本例为配方A，如果需要指定其他值作为参考值，则要在“选项”（见图9—39中右上）给出），下面我们将介绍不同的参考值的含义。在配方为B时，应加上-5.1900，因而得到其常数项为28.9178－5.1900＝23.7278（其p值为0.000，说明配方A与配方B在回归方程常数项上有显著差异）。在配方为C时，应加上-27.4400，因而得到其常数项为28.9178－27.4400＝1.47782（其p值也为0.000，说明配方A与配方C在回归方程常数项上有显著差异），回归方程中的温度及温度的平方项上之p值分别为0.000及0.017，也都是显著的。

此计算结果还告诉我们模型总效果是高度显著的，衡量回归效果的决定系数R²＝0.9770；调整的决定系数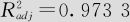；一切看来都很好。虽然第5号观测值的残差较大，但也并不严重。残差图也基本正常。

但我们仔细观察图9—43可以发现，对于3种不同的配方其响应变量的图形是有差别的：在配方A（低铬、镍）时弯曲不严重，而配方B，C（高铬、镍）时弯曲明显。如果不同的配方会导致不同的回归关系，我们应该考虑配方与温度的交互作用。为此，我们先考虑配方与温度的交互作用（方案2）。这时模型项中应该包含“配方|温度”及“温度*温度|配方”。方案2的模型表示方法见图9—44中右侧。其计算结果如下：

回归方程

模型汇总

方差分析

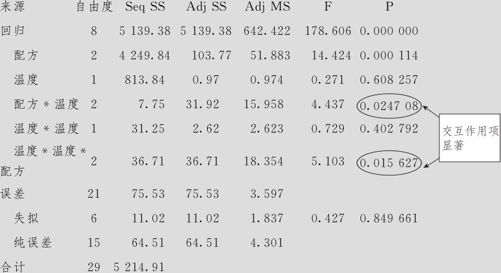
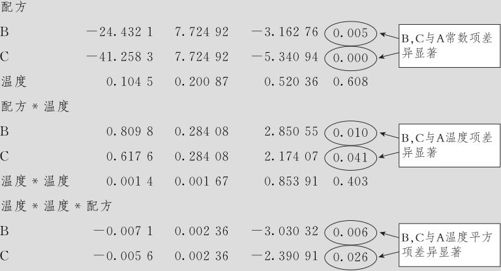
这时的方程不但按配方的不同分为3个回归方程，而且它们的回归系数是不同的（对于温度项和温度的平方项）。其计算方法是这样的：在回归系数列表中，配方A的常数项为39.9380，在配方B时，应加上-24.4321，因而得到其常数项为39.9380－24.4321＝15.5059（此项p值为0.005，说明配方B的常数项与配方A的常数项有显著差异）；在配方C时，应加上-41.2583，因而得到其常数项为39.9380－41.2583＝-1.3204（此项p值为0.000，说明配方C的常数项与配方A的常数项有显著差异）。在回归方程中温度项，配方A的系数为0.1405，在配方B时，应加上0.8098，因而得到其常数项为0.1045＋0.8098＝0.9143（此项p值为0.010，说明配方C的温度项与配方A的温度项有显著差异）；在配方C时，应加上0.6176，因而得到其常数项为0.1045＋0.6176＝0.7221（此项p值为0.041，说明配方C的温度项与配方A的温度项有显著差异）。在回归方程中温度平方项，配方A的系数为0.0014，在配方B时，应加上-0.0071，因而得到其常数项为0.0014－0.0071＝-0.0057（此项p值为0.006，说明配方B的温度平方项与配方A的温度平方项有显著差异）；在配方C时，应加上-0.0056，因而得到其常数项为0.0014－0.0056＝-0.0042（此项p值为0.026，说明配方C的温度平方项与配方A的温度平方项有显著差异）。可以断言现在的回归方程是合乎要求的回归方程。

总之，根据上述分析可以断言，配方B与配方A的回归方程有显著差异，配方C与配方A的回归方程有显著差异。但是配方B与配方C的回归方程间是否有显著差异？上述结果并未回答。为此，我们选择配方B作为参考值，只需要在“选项”框内填写“配方‘B’”（见图9—45）即可（注意：填写时“配方”与“B”之间要有空格，“B”用半角状态双引号）。

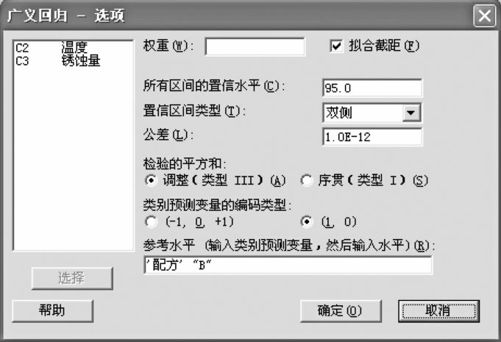
图9—45　广义回归指定参考值的操作图

再进行一次回归后，结果如下：

回归方程

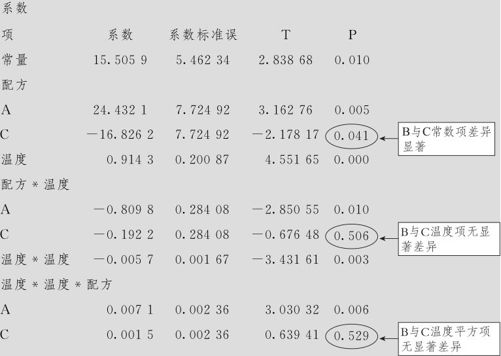
上述系数的具体计算从略。从上述结果可以确认：在配方B与配方C间，常数项有显著差异（p值为0.041），温度项系数无显著差异（p值为0.506），温度平方项也没有显著差异（p值为0.529），因此，在配方B与配方C间，其显著差异完全是由于常数项的不同而引起的；在配方B与配方A之间，其显著差异既有常数项的不同，也包含温度及温度的平方项系数的不同。

例9—11和例9—12都是广义回归中最简单的情况。一般来说，连续型的回归自变量可以是多个；类别变量也可以是多个。多个连续型的回归自变量的情况我们早就见过（这就是多变量的回归问题），而多个类别变量的情况将导致有多个分叉的结构，这里的分叉是所有的类别变量的所有搭配都应该有相应的回归方程，一般是比较复杂的，这里就不仔细讨论了。