11.2　偏倚和线性

11.2.1　偏倚

偏倚是指多次测量的理论上的平均值μ与其参考值V_r之间的差异。参考值的来源主要有：多个准确测量设备所得重复测量值的平均值；专业团体认可的值；当事方达成一致的值或法律规定的值。实际工作中，测量系统分析对某个指定参考值只能进行有限几次重复测量，我们观测到的只能是样本的平均值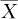。因为测量中总会存在随机误差，每次测量结果总会有波动，也就会有波动。即使μ与其参考值V_r相等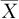，也不见得正好与其参考值V_r相等。研究偏倚首先要明确到底是否存在偏倚，也即判断测量结果的理论上的均值μ是否等于参考值V_r。这正好是单样本假设检验所要解决的问题。有的偏倚看似很小，但检验结果证实偏倚确实不为0；有的偏倚看似数值不小，但由于精确度较差，反而检验结果证实偏倚为0。一切要在检验之后才能得到结论。

经过检验，可能断言是“在此点处，测量系统没有偏倚”，也可能断言是“在此点处，测量系统确实有偏倚”。如果确有偏倚，就用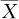－V_r作为此点处偏倚的估计。这里需要注意的是：偏倚的值可正可负，其绝对值则用来作为准确性的代表。

此外，在整个量程中，各点处的偏倚可能并不相等，整体偏倚的状况可以用偏倚平均值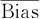与过程总波动PV（PV＝6σ_总）比值的形式，即偏倚百分率％Bias表示，它的数学表达式为：

这里请注意，偏倚有正有负，偏倚平均值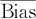是把正负偏倚抵消了算出的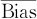，很小不代表各处偏倚都很小。另外，对于％Bias很难给出一个对任何测量系统都能认可的统一标准，要根据自己生产过程的特性来判断，但肯定这个数值要很小（％Bias通常要小于10）才行。

11.2.2　线性

偏倚是针对单点处而言的，而每个测量系统都会有量程作为测量结果的范围。原则上说应当要求量程内的任何一处都不存在偏倚，这才是最好的测量系统。但是如果在一点处能够准确地知道偏倚的数值，或者在整个量程范围内有共同的偏倚，则可以通过扣除偏倚加以修正。但测量系统分析只可能在量程中的某几个点进行，那么怎样才能对整个量程的每一点都知道偏倚值呢？如果可以断言测量系统的偏倚在整个量程范围内具有线性，则可以根据已有的测量结果加上线性关系的规律求出任一指定点处的偏倚。这是我们在有偏倚的条件下的“不幸中的万幸”；如果有偏倚而又不具有线性，则将真是大不幸，测量系统已经无可救药了。

具体来说，线性是指在测量系统预期的量程范围内，各点处的偏倚与参考值呈线性关系。一般来说，线性就是要求这些偏倚量在数学上表现为是其对应参考值的线性回归关系。如何根据多点处的偏倚求出线性回归方程，以及如何判断回归方程的斜率不为0，这正是第9章讨论过的回归分析内容。偏倚是否有线性，可以用图11—4中的两种形式来说明。

通常用线性度Linearity衡量某个量程的偏倚的总体变化程度，其定义是线性方程斜率b的绝对值与过程总波动PV的乘积，即

此量代表过程总波动范围内，测量值偏倚的波动（注意不是偏倚本身）范围。

量程的偏倚的总体变化程度也可以用百分比的形式，即线性百分率％Linearity表示，它的数学表达式为：

换言之，％Linearity就是将|b|写成百分数罢了。即

对于线性的图示可参见图11—4。一般情况下，类似于左图的表达形式使用得更多一些，这是因为偏倚与被测值相比会非常小，图11—4右图中的两条线常常分辨不开，因而很难精确画出。

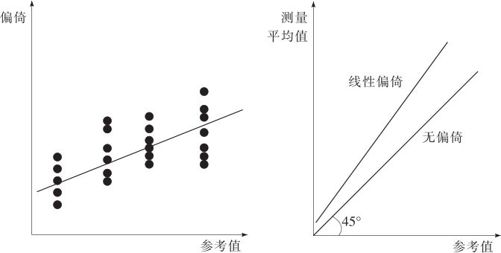
图11—4　偏倚的线性示意图

11.2.3　偏倚和线性的计算

实际工作中，常常同时评估偏倚和线性。在量程范围内，将偏倚作为y，参考值作为x，进行简单线性回归分析，计算出线性回归方程：y＝a＋bx，构建此数学模型，绘制出如图11—5所示的图形。从图11—5中可以看出，在若干点上有偏倚，偏倚为0的水平线已落入回归线的置信区间带之外了。

图11—5　偏倚的线性回归拟合线

经过统计检验，如果各点上都没有偏倚，而且回归效果不显著，a和b均为0，则称测量系统在整个量程范围内没有偏倚。在回归拟合线图中，则表现为偏倚为0的水平线（Bias＝0）完全被包含在回归线的置信区间带之内，且各点的平均偏倚值皆落在回归线的置信区间带之内，则这时测量系统的偏倚和线性均合乎要求，是测量系统中偏倚和线性最理想的状况。

如果在若干点上有偏倚，偏倚为0的水平线（Bias＝0）已经落入回归线的置信区间带之外，这时如果不能拒绝回归系数b为0，但a显著不为0，则称在整个量程范围内有共同偏倚a（即有常量偏倚）。这虽然比最理想状况稍差，但由于偏倚有共同值，因而在使用时容易通过纠偏加以修正。

如果量程范围内有若干点偏倚不为0，偏倚为0的水平线（Bias＝0）已经落入回归线的置信区间带之外，且回归效果显著，即系数b显著不为0，同时各点的平均偏倚值皆落在回归线的置信区间带之内（参见图11—5），这时则称在整个量程范围内偏倚有线性（即有非常量偏倚），此时可以计算出线性产生的影响。这是不幸中的万幸，因为毕竟在使用该测量系统时，对于所有测量结果可以按线性回归结果对偏倚加以修正。

如果量程范围内有若干点偏倚不为0，但又不能拒绝回归系数b为0，而且有若干点处的平均偏倚值落在回归线的置信区间带之外（且位于不同侧），则测量系统在整个量程中有偏倚，但又因没有线性而无法加以修正，这是测量系统中最差的情况。这样的测量系统根本无法修偏，只能弃之不用。

接下来，用例11—1对测量系统的偏倚和线性分析方法加以说明。

例11—1

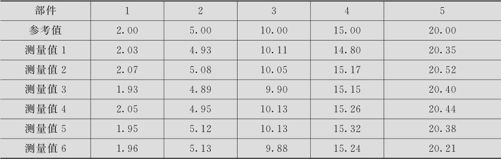
一家公司的质检部门新购买一台测厚仪，在正式使用之前，需要对此测量系统进行评估。根据实际需要的量程范围，挑选了5个具有代表性的标准部件。然后由检验员以随机的方式对每个部件测量了6次。假设已知过程总波动PV（即6倍的过程标准差）为12，试分析其偏倚和线性（数据列在表11—1中，数据文件：QT_MSA偏倚与线性.MTW）。

表11—1　测厚仪的测量结果

请注意，MINITAB中的数据与表11—1的形式并不一样，要将部件号、参考值与测量值分列在3列中（见图11—6中的最右端）。

计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞量具研究＞量具线性和偏倚研究（Stat＞Quality Tools＞Gage Study＞Gage Linear&Bias Study）”进入（见图11—6）。

图11—6　测量系统偏倚的线性计算操作图

2．指定“部件号（Part numbers）”为“部件”，“参考值（Reference value）”为“参考值”，“测量数据（Measurement data）”为“测量值”，在“过程变异（Process variation）”中输入“12”，运行命令后可以得到图11—7。

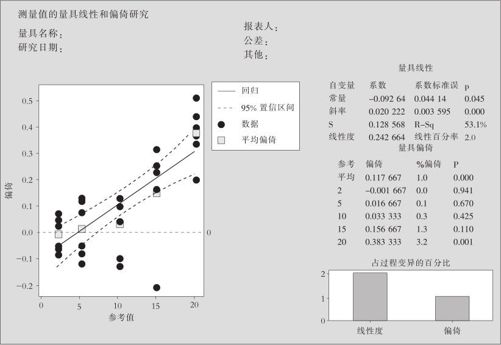
图11—7　线性与偏倚的分析图

从图11—7中可以看到下述分析结果：整体偏倚值＝0.117667，整体偏倚百分率＝1.0，因为对应的p值＝0.000＜0.05，所以判定整体偏倚确实存在。同时，还可以查阅到5个具有代表性的测量点的偏倚值和偏倚百分率，其中在参考值为20时，偏倚严重存在。线性度＝0.242664，线性百分率＝2.0，表明当需要测量的部件的波动范围在12（已知条件）之内时，测量的偏倚值的波动保持在0.242664的范围内。偏倚的线性回归拟合方程是y（偏倚）＝－0.09264＋0.020222x（参考值），因为斜率和截距相应的p值都小于0.05，式中的斜率和截距都显著地不为0，结合左侧带拟合直线的散点图，表明此测试设备在整个量程范围内有线性偏倚。实际使用此测量系统时，可以对于测定出的x值，按上述回归方程计算出偏倚值，然后对测量结果加以修正。