10.2　变异源分析的一般方法

先引入一些在进行变异源分析（SOV）中最常用到的概念。我们把最能代表过程特征的变量称为因变量或响应变量，而把可能产生影响的那个（些）变量称为因子。此因子在观察中可能取的不同值称为水平。例如，有3台车床，称车床这个因子取3个水平。在SOV中，因子通常是以离散型变量形式出现的，即使原来是连续型变量也要在取定若干固定数值后将其变成离散型变量。对于因子和响应变量都是连续变量的情况，通常会用回归分析的方法来处理；对于两者皆为离散型变量的情况，通常会用列联表的卡方检验方法来处理；如果因子是连续变量而响应变量是离散数据时，则使用Logistic回归处理。在SOV研究中，表面上看，因子是以离散型变量形式出现的，响应变量是以连续型变量形式出现的，这种类型问题都可以使用ANOVA的方法处理。但实际上，由于每个因子的性质可能不同，各因子间还可能有多种不同的结构关系，因此处理起来也要分为多种类型，要在ANOVA的基础上进一步深入计算，其细节将在下面分别介绍。

变异源分析是指通过对过程收集到的数据进行分析得到关于变异来源的结论。但是如何收集数据呢？比如，我们关心本车间生产的螺钉的直径的波动问题，到仓库中随机抽取200颗螺钉，发现它们直径的方差大得超出我们的想象。螺钉的直径是关键指标，减小它的波动对于生产来讲是很重要的问题。但这样随机收集的数据能说明什么？它只能说明产品性能的总体波动太大，而我们所希望获得的是更进一步的信息，即到底是什么原因造成这么大的波动。为此必须放弃简单随机抽样，改而采用按不同因子的不同水平有计划地分层，然后再抽取样本。再有就是，抽样一定是在现有生产条件下进行的，并不对生产条件作任何改动，抽样分析工作只是有计划的观察，这与试验设计中的状况是完全不同的。形象些说，我们只是对现实状况作最准确详尽的记录，并加以分析，得到各个因子在产生响应变量的变异方面的贡献率，从而确认减少变异的主攻方向。这很像选好角度给过程拍一个有很多细节的“快照”，我们当然希望快照中能准确而又详细地反映出过程全部真实的状况，而并不希望过程本身发生任何变化。

我们通常就是按上述方法进行变异源分析的。为使大家有具体的了解，先看下面的例子。

例10—1

考虑车工车间在生产标准螺钉时的直径波动过大问题。从十几名工人中随机选取3名工人，让他们使用同一根钢条做原料，每人都使用自己平时所用的车床，按随机顺序各自分别加工出4颗螺钉，然后在每颗螺钉的根部随机选取两个相互垂直的方向，分别测量其直径，共得到24个数据。分析螺钉直径间的变异产生的原因。其数据列于表10—1中（数据文件：QT_SOV2嵌套.MTW）。

表10—1　螺钉直径数据（2因子）

很显然，工人之间可能有变异，每名工人自己生产的螺钉间也有变异。当然，在一颗螺钉根部两个方向上测定的直径间也有变异，但我们是用其平均值作为整个螺钉直径的代表的，两个不同方向间变异的产生是车床生产过程中固有的（称为“不圆度”），它是在同一名工人生产出同一颗螺钉上得到的结果。我们目前还不想讨论螺钉不圆度的成因，它的产生几乎是不可控制的，我们将把它作为随机误差来处理。当然在实际工作中，它可能含有测量误差，但在测量系统分析完成后，我们可以假定测量误差已经小到可以忽略的程度了。随机误差并不是测量误差，但它是完全随机形成的，不能算作待考察的因子。总之，现在有“工人”和“螺钉”两个因子以及一个随机误差项（或螺钉内部变异）。我们的问题是，在螺钉直径的变异中，在“工人”、“螺钉”这两个因子和随机误差项之间，也即在3名工人间和每人生产的4颗螺钉间以及螺钉内部的变异中，究竟哪项最大，哪项次之，哪项最小？它们各占多大比例？

将此例题所叙述的问题一般化，就是进行SOV时的处理方法。先要根据过程分析结果，初步判断可能影响响应变量的因子。当然，在准备进行SOV分析前，先要确认测量系统是合格的，也就是说，由测量引起的波动应该控制在非常小的范围内。只有当测量系统被判定为合格时，收集到的数据才能用来进行SOV分析。至于测量系统分析的内容，从使用的工具来看也与SOV有关，我们将在下一章讨论。

通常把变异来源归因于下述三个方面：

1．随机误差

任何实际工作中，都要先选取一个可以不追究或无法更细致追究的变异原因，我们把这部分称为随机误差。有时也称为“组内差”，如上例的不圆度误差。注意不要把这部分理解为或实施为重复测量的误差，我们需要的是真正反映过程中的随机误差项，像例10—1中螺钉两个垂直方向的直径度量差别就是较好的选择。

2．组间差

经常要考虑人员之间的差异、部件间的差异、原料批次间的差异、设备之间的差异、方法之间的差异、环境条件之间的差异等。这些是我们要考察的重点，而且对于不同问题将会有不同的安排与选择。例如在例10—1中，考虑3个工人间变异、每人生产的4颗螺钉间变异就都是组间差。

3．时间差异

需要考虑到时间因素所形成的变异。例如，每周之间的差异、每周内5个工作日之间的差异、早中晚三班之间的差异、每个小时之间的差异等。

SOV最终的目的就是把整个方差分解为若干有意义的方差分量。如果将因子用A，B，…，K代表，将随机误差用E代表，则有基本公式：

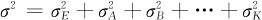
SOV最后的结果就是要得到上式的数值结果，并且能把各项方差在总方差中所占的比率计算出来，从而确认对于总方差的最大贡献者（或言“罪魁祸首”）。

选定SOV所要研究的因子后，要设计好采样计划。除了随机误差因子可以最少取2个水平之外，任何属于组间差或时间差异的因子都最少取3个水平。使用变异源分析方法的第一个重要步骤是，先画出SOV中要考察的各因子间的树状图（tree diagram）。每个因子画一行，将各水平的数值从左至右列出，然后对每个因子都自上而下画出。这时，由于随机误差总会放在最底（下）层，这行不能算是“因子”。例10—1的树状图参见图10—1。

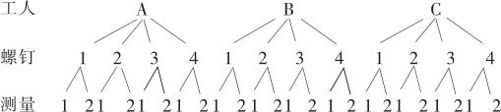
图10—1　例10—1螺钉直径（2因子）树状图

按照上述树状图，我们安排了数据的收集工作，最终得到了如表10—1中列出的观测值。

为了解更广泛的情况，再看几个例子。

例10—2

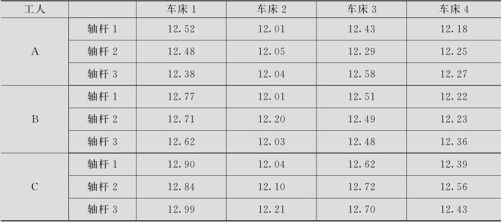
考虑精密车工车间生产微型轴杆长度波动过大问题。我们从十几位工人中随机选取3名工人，让他们使用同一根钢条做原料，大家都使用固定的编好号的4台车床，按随机顺序各自分别加工出3根轴杆，然后分别测量其长度，共得到36个数据。我们要分析轴杆长度间变异产生的原因，究竟是车床间的变异为主？还是工人间的变异为主？还是同一工人同一车床生产的不同轴杆间的变异为主？其数据列于表10—2中（数据文件：QT_SOV2交叉.MTW）。

表10—2　轴杆长度数据

这仍然是两个因子的问题，下面看一个更复杂些的例子。

例10—3

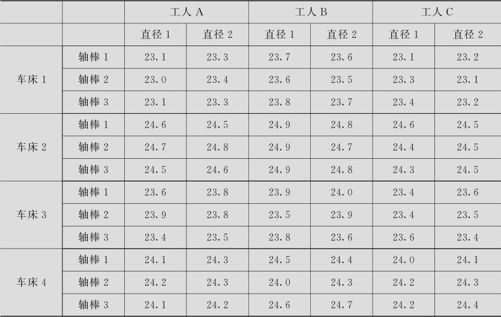
轴棒直径变异问题（3因子）。对于随机选取的3名工人A，B及C，让他们使用同一根钢条做原料，分别使用已选好并编了号的固定的4台车床，各自分别加工出3根轴棒，然后在每根轴棒的根部随机选取两个相互垂直的方向，分别测量其直径，共得到72个数据。我们的问题是，轴棒直径间的变异究竟是怎样产生的？这里考虑了工人、车床及轴棒共3个因子，其数据列于表10—3（数据文件：QT_SOV3交叉嵌套.MTW）。

表10—3　轴棒直径数据（3因子）

对于这种分析变异来源的问题，在统计上如何处理呢？通常有两个步骤：首先应用统计作图法，提供图形工具直观显示这些变异的组成状况（严格说这是用计算机将图形显示出来的问题，与统计概念无关）；然后给出精确数值定量的分析和解释，将各因子的贡献量化。下面先在10.3节中介绍变异源分析的图形方法，然后在10.4节中介绍变异源分析的单因子数值分析方法，最后在10.5节中介绍多种更复杂模型的分析方法。