4.1　正态总体的抽样分布

为了对正态总体的统计量进行分析，首先要了解它们的分布，各统计量的分布称为抽样分布，这里介绍四种常用的抽样分布。

4.1.1　样本均值的分布——标准正态分布及T分布

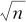从2.5节中心极限定理所叙述的结论，我们可以得知的标准差是原来的标准差除以，因此可以得到如下结论：

当总体服从正态分布N（μ，σ²）时，样本均值服从正态分布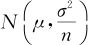，若将样本均值进行标准化转换，则有

也就是说，当总体标准差σ已知时，样本均值进行标准化转换后，可以得到标准正态分布。

当总体标准差σ未知时，用样本标准差S代替总体标准差σ后会怎么样？20世纪初，人们都认为，代换后正态分布将近似不变。但年轻的统计学家戈塞特（W. S. Gossett）在研究时发现：当样本量很小时，用样本标准差S代替总体标准差σ后，分布与正态分布有很大不同，波动大大增加了（即其分布密度图形比正态分布的要“胖”很多），而且波动与样本量关系密切（样本量越小，密度图形越“胖”）。1908年，戈塞特（Gosset）以笔名“Student”发表一篇论文，给出了一种新分布。这篇文章成为近代统计学开始的里程碑，他所建议的分布被称为“学生氏t分布”。也就是说，用样本标准差S代替总体标准差σ后，原来的Z统计量会变成t统计量，服从自由度为n－1的t分布，记为t（n－1），即

式中，S是样本标准差，其计算公式为：

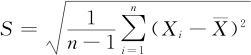
这里省略其证明过程，有兴趣的读者可以参考一般的概率统计教材。大家只要记住式（4—2）的结论就可以了。

在实际工作中，总体标准差σ常常是未知的，因此t统计量常用来进行有关单个正态总体的均值和两个正态总体均值之差等问题的假设检验。

t分布的概率密度函数与标准正态分布其实很类似，亦为对称分布，均值也为0。与标准正态分布相比，t分布的密度曲线只是略“胖”些罢了（见图4—1）。这是因为将式（4—2）与式（4—1）相比较后可以看出，t统计量除了分子的样本均值是随机变量外，分母用随机变量样本标准差S代替常数总体标准差σ，其波动性增加了，故t的标准差比标准正态Z的标准差大。当然，自由度超过30以后，二者差别很小，此时完全可以用标准正态分布替代t分布。

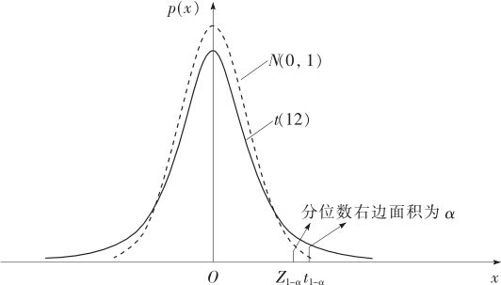
图4—1　标准正态密度与t分布密度的比较

t分布（Student t distribution）的定义是：如果X服从标准正态分布，S²服从ν个自由度的卡方分布，且它们相互独立，那么随机变量

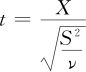
所服从的分布称为ν个自由度的t分布。其分布密度函数为：

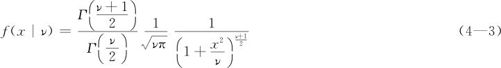
当ν→∞时的极限分布即是标准正态分布，当ν＝1时就是Cauchy分布。t分布只包含1个参数ν。数学期望和方差分别为0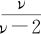，（ν≤1时期望不存在，ν≤2时方差不存在）。我们常常用t（ν）表示ν个自由度的t分布。MINITAB对于更一般的t分布还增加了一个“非中心参数”，当非中心参数为0时，就得到了我们现在所说的t分布。在用MINITAB计算时，只要注意这一点就行了。

在统计推断中常常会碰到自由度这一概念，不少人对这一概念感到不好理解，这里特别解释一下。

如果有10个数，而且你知道了均值和其中的9个数的值，那么你就可以推算出第10个数。又比如，让10个人挑选总共10个不同颜色的玻璃球，只有9个人有自由挑选的可能，因为当这9个人都挑好之后，你就别无选择了！因此这个问题的自由度为9。

所以，自由度通常可以简单地理解为在研究问题中，可以自由独立取值的数据或变量的个数。

例4—1

计算下列各分布的相关数值。

（1）Z～N（0，1），求Z＝1.98时的概率密度。

解　1）选择“计算＞概率分布＞正态分布（Calc＞Probability Distributions＞Normal Distribution）”，选中“概率密度（probability density）”，输入常数“1.98”（如图4—2所示）。

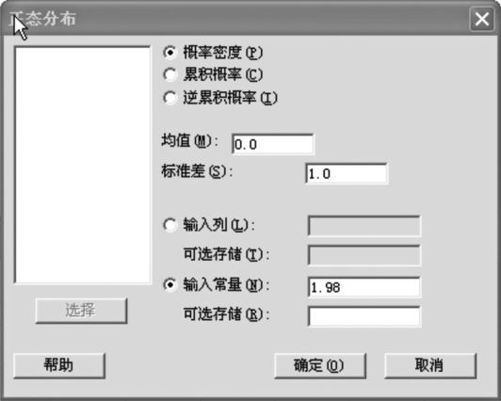
图4—2　正态分布概率密度计算操作图

2）点击“确定”后，得到如下输出结果：

概率密度函数

正态分布，均值＝0和标准差＝1

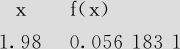
（2）Z～N（0，1），求P（Z ＜2.4）。

解　1）选择“计算＞概率分布＞正态分布（Calc＞Probability Distributions＞Normal Distribution）”，选中“累积概率（cumulative probability）”，输入常数“2.4”（见图4—3）。

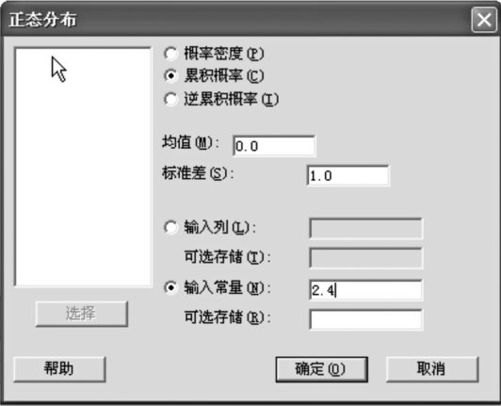
图4—3　正态分布累积概率计算操作图

2）点击“确定”后，得到如下输出结果：

累积分布函数

正态分布，均值＝0和标准差＝1

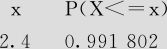
（3）Z～N（0，1），求使得P（Z ＜x）＝0.95成立的x值，即Z的0.95分位数。

解　1）选择“计算＞概率分布＞正态分布（Calc＞Probability Distributions＞Normal Distribution）”，选中“逆累积概率（Inverse cumulative probability）”，输入常数“0.95”（见图4—4）。

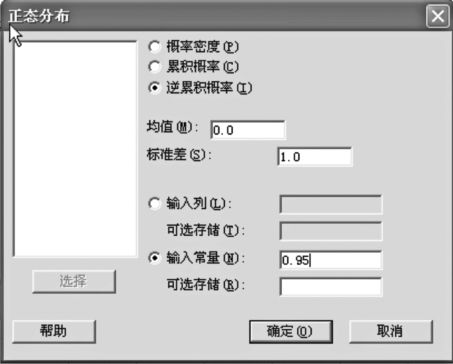
图4—4　正态分布分位数计算操作图

2）点击“确定”后，得到如下输出结果：

逆累积分布函数

正态分布，均值＝0和标准差＝1

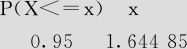
此结果很重要，正态分布的0.95分位数（或右侧0.05分位数）是1.645。

（4）自由度＝12，求使得P（t＜x）＝0.95成立的x值。

解　1）选择“计算＞概率分布＞t分布（Calc＞Probability Distributions＞t Distribution）”，选中“逆累积概率（Inverse cumulative probability）”，输入自由度“12”，常数“0.95”（见图4—5）。

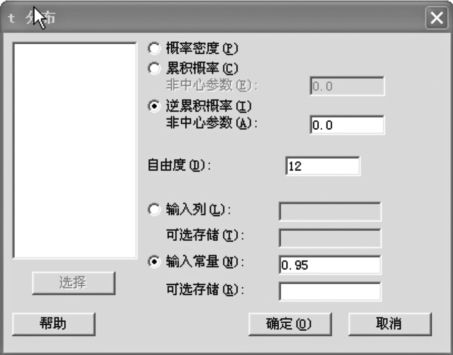
图4—5　t分布分位数计算操作图

2）点击“确定”后，得到如下输出结果：

逆累积分布函数

学生t分布，12自由度

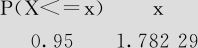
在本书的附表3中，查表得到的结果是1.782。此结果从数值上说明：同样的0.95分位数，也就是同样从右侧截取0.05面积，正态分布的横坐标是1.645，而t分布的横坐标就要大很多：12个自由度时是1.782；6个自由度时是1.943；2个自由度时是2.920；1个自由度时竟然高达6.314。

（5）自由度＝12，求P（t≤3）。

解　1）选择“计算＞概率分布＞t分布（Calc＞Probability Distributions＞t Distribu-tion）”，选中“累积概率（cumulative probability）”，输入自由度“12”，常数“3”（见图4—6）。

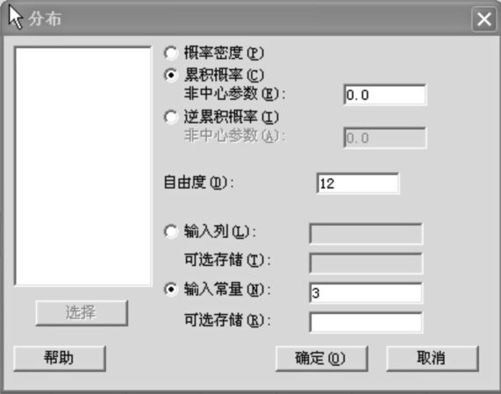
图4—6　t分布累积概率计算操作图

2）点击“确定”后，得到如下输出结果：

累积分布函数

学生t分布，12自由度

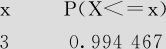
4.1.2　双样本均值差的分布

设有两个总体：X～N（μ₁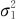，），Y～N（μ₂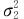，），从总体X中抽取的样本X₁，X₂，…，X_n，样本均值为，样本方差为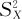，样本标准差为S_X，从总体Y中抽取的样本为Y₁，Y₂，…，Y_m，样本均值为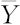，样本方差为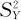，样本标准差为S_Y。

根据两个总体的方差是否已知或相等，其样本均值之差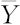－服从的抽样分布有以下三种情况：

（1）两个总体均服从正态分布，且两个总体的方差均已知情况时，两样本均值差所服从的抽样分布为：

将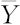－标准化，得到Z统计量：

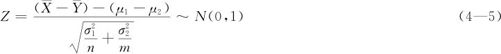
只要样本量足够大，对于总体分布是否正态都可近似使用。

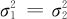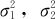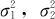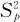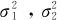（2）两个总体均服从正态分布，且，但均未知时，两样本均值差所服从的抽样分布为：，由于均未知，我们需要用样本合并方差取代，即

进行标准化变换后，得到

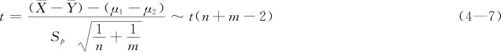
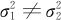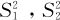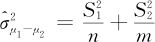（3）当两个总体均服从正态分布，，且方差均未知时，自然用分别估计，从而得到，此时

需注意的是：此时t不再服从自由度为n＋m－2的t分布，而是近似服从自由度为ν的t分布。自由度ν的计算公式为：

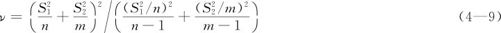
4.1.3　正态样本方差S²的分布——卡方分布

若X₁，X₂，…，X_n是从正态总体N（μ，σ²）中抽出的一组样本量为n的独立随机样本，记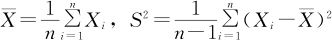，则当μ已知时：

当μ未知时，用代替μ后可以得到

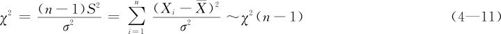
其概率密度函数在正半轴上呈正偏态分布，如图4—7所示。

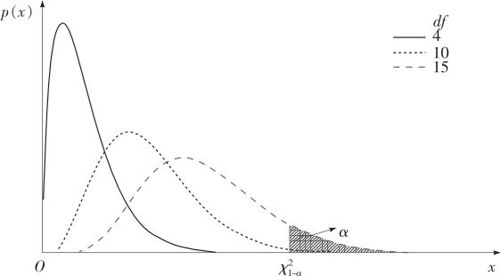
图4—7　卡方分布密度图

卡方分布的定义是：把n个相互独立的标准正态随机变量的平方和称为自由度为n的卡方分布（χ是希腊字母，χ²写成英文是Chi-square）。它的密度表达式为：

式中，参数ν≥1称为自由度。卡方分布有向右的偏斜，特别在较小自由度情况下（ν越小，分布越偏斜）。我们常用χ²（ν）表示自由度为ν的卡方分布。MINITAB软件提供的是一个更一般的“非中心”卡方分布，表达式（4—12）是其中最简单的“中心参数”为0的情况，使用MINITAB时只要注意这点就够了。

另外，卡方分布是Gamma分布b＝2时的特例。由于卡方分布在正态抽样定理中的重要性，因而卡方分布受到特别的重视。卡方分布有很多用途，其中一项就是用来分析单个正态总体样本方差的状况。卡方分布还可以用来进行分布的拟合优度检验，也即检验资料是否符合某种特定分布；对于离散数据构成的列联表，也可以用来分析两个离散型因子间是否独立等，这些将在以后的章节予以介绍。

卡方分布的性质：

（1）卡方分布的加法性：设X和Y彼此独立，且都服从卡方分布，其自由度分别为n₁，n₂。若令Z＝X＋Y，则Z服从自由度为n₁＋n₂的卡方分布。

（2）若X～χ²（n），则E（X）＝n，V（X）＝2n。

例4—2

计算下列各卡方分布的相关数值：

（1）自由度＝10，求使得P（χ²＜x）＝0.95成立的x值。

解　其实这就是求卡方分布的分位数问题。我们的书后以及一般的概率统计教材都会附有这张分位数表，现在我们自己可以用计算机把它们计算出来了。

1）选择“计算＞概率分布＞卡方分布（Calc＞Probability Distributions＞Chi-square）”，选中“逆累积概率（Inverse cumulative probability）”，输入自由度“10”，常数“0.95”（见图4—8）。

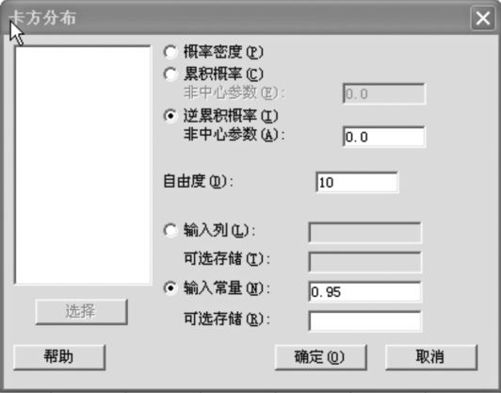
图4—8　χ²分布逆累积概率计算操作图

2）点击“确定”后，得到如下输出结果：

逆累积分布函数

卡方分布，10自由度

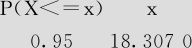
大家可以查本书的附表4验证，查表给出的结果是18.31。

（2）自由度＝10，求P（χ²≤28）。

解　1）选择“计算＞概率分布＞卡方分布（Calc＞Probability Distributions＞Chi-square）”，选中“累积概率（cumulative probability）”，输入自由度“10”，常数“28”（见图4—9）。

图4—9　χ²分布累积概率计算操作图

2）点击“确定”后，得到如下输出结果：

累积分布函数

卡方分布，10自由度

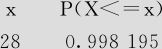
4.1.4　两个独立的正态样本方差之比的分布——F分布

两个独立的正态样本方差之比的分布是F分布。设有两个独立的正态总体N（μ₁，σ²）和N（μ₂，σ²），它们的方差相等。又设X₁，X₂，…，X_n是来自N（μ₁，σ²）的一个样本；Y₁，Y₂，…，Y_m是来自N（μ₂，σ²）的一个样本，这两个样本相互独立。它们的样本方差之比是自由度为n－1和m－1的F分布：

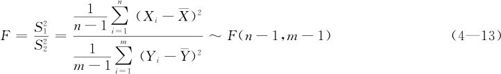
式中，n－1称为分子自由度；m－1称为分母自由度；F分布的概率密度函数在正半轴上呈正偏态分布（见图4—10）。图4—10画的是分子自由度为2，分母自由度分别为5及20的两条密度曲线。

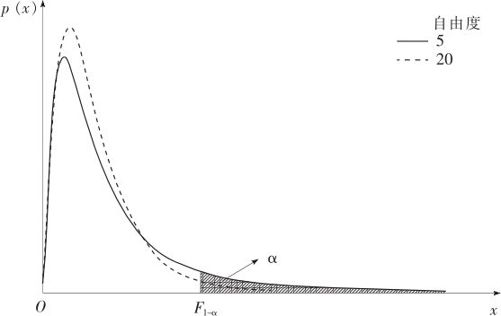
图4—10　F分布密度图

实际上，F统计量就是由两个卡方随机变量相除所构成的，如果X～χ²（ν₁），Y～χ²（ν₂），且二者相互独立，则称二者比值的分布为F分布，即

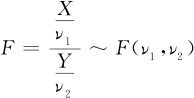
其密度函数是：

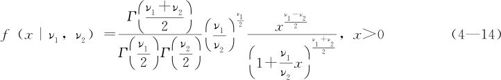
F分布的应用非常广泛，尤其是在判断两正态总体方差是否相等以及方差分析（ANOVA）等问题上面。

例4—3

计算F_0.95（8，18）的数值。

解　1）选择“计算＞概率分布＞F分布（Calc＞Probability Distributions＞F Distribution）”，选中“逆累积概率（Inverse cumulative probability）”，分别输入分子、分母的自由度“8”，“18”，常数“0.95”（见图4—11）。

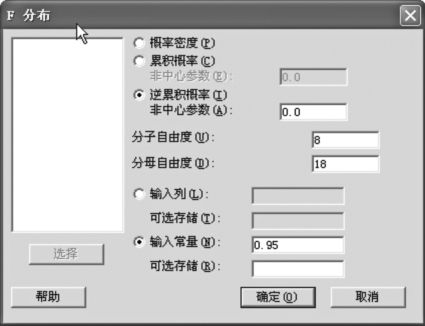
图4—11　F分布分位数计算操作图

2）点击“确定”后，得到如下输出结果：

逆累积分布函数

F分布，8分子自由度和18分母自由度

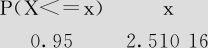
读者可以查本书附表5，查表的结果是2.51。