12.4　特殊控制图

在12.1节中介绍了所有的常规控制图：单值—移动极差图、均值—极差图、均值—标准差图、不合格品率图、不合格品数图、单位产品缺陷数图和缺陷数图。除这些常规控制图，还有一些特殊的控制图，如累积和控制图（CUSUM Chart）、指数加权移动平均控制图（EWMA Chart）、标准化控制图（Z-MR Chart）、区域控制图（Zone Chart）和多元控制图（Multivariate Chart）等。本节将介绍特殊控制图中比较常用的指数加权移动平均控制图和标准化控制图。

12.4.1　指数加权移动平均控制图

常规控制图的运用前提是假定观测值服从正态分布和过程均值恒定不变。但在实际应用中，这些假定不一定都能成立。在过程均值有长期的微小漂移时，常规控制图对于过程均值的微小漂移很不敏感，很难识别过程的这种变化；相比较而言，指数加权移动平均（exponential weight moving average，EWMA）控制图的最大优点是不受正态假定条件的限制，同时由于EWMA控制图上的点包含了所有前面子组的信息，因而也能够较敏感地探测出过程均值的微小漂移。此外，EWMA控制图还适用于单个观测值及子组均值两种情况。

在EWMA控制图中，绘制的统计量Z为当前值与历史数据的加权平均，以子组均值控制图为例，其计算公式为：

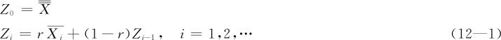
式中，r为当前观测值的权重，取值范围为［0，1］。

我们分析一下式（12—1）的含义。这里第i个新的统计量Z_i包含两部分：一部分是第i个观测值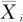，它以权重r加入；另一部分是前面的统计量已取得之值Z_i－1，它以权重1－r加入。多次使用式（12—1）降低下标值后可以发现，离指标i越远（即越早期）的数据被赋予的权重将按指数速度减小。这样一来，Z_i的值不仅考虑了第i个时刻的观测值而且考虑其历史数据，因而能够较好地反映出趋势性的状况，而且使曲线变得比原始数据光滑得多。r值越小，则光滑的效果越好；r值越大，则保真的效果越好，即光滑的效果越差；但一般建议0.05≤r≤0.25。可以先缺省设定（默认）r＝0.2。如果已发现有异常点，则可以判断出现异常而终止判断过程；如果发现可疑趋势，但对于此权重取值并未超界，则可以换用较小或较大的权重r试验一下，只要某个权重使得数据点出界，我们都可以判断“过程出现异常”，或说过程已失控。关于此类控制图中控制线的计算公式已整理成表12—9。

表12—9　指数加权移动平均控制图中控制线的计算公式

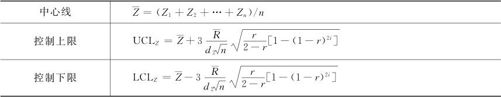
下面用例12—6对EWMA控制图的实际应用加以说明。

例12—6

某电子厂的QC小组欲优化芯片研磨过程，首先对其厚度进行SPC控制。小组共收集20个厚度数据，试用控制图分析该过程的稳定情况（数据列在表12—10中，数据文件：SPC_EWMA控制图.MTW）。

表12—10　芯片研磨厚度数据表

解　首先，用计算机软件MINITAB实现常规控制图I-MR：

1．从“统计＞控制图＞单值的变量控制图＞I-MR（Stat＞Control Charts＞Variable Chartsfor Individuals＞I-MR）”进入。

2．指定“变量（Variables）”为“厚度”，运行命令后得到图12—12。

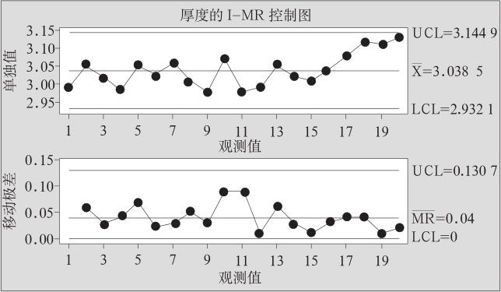
图12—12　芯片研磨厚度的I-MR控制图

由图12—12可知，I-MR控制图中最后几个点虽有上扬的趋势，但使用传统的8条判异准则没有发现任何可判异问题，只能判生产正常。由于最终部分似乎有向上升的不正常趋势，下面用计算机软件MINITAB绘制特殊控制图EWMA：

1．从“统计＞控制图＞时间加权控制图＞EWMA（Stat＞Control Charts＞Time-Weighted Charts＞EWMA）”进入。

2．指定“图表的所有观测值均在一列中（All observations for a chart are in one column）”为“厚度”，指定“子组大小（Subgroup sizes）”为“1”，运行命令后得到图12—13。

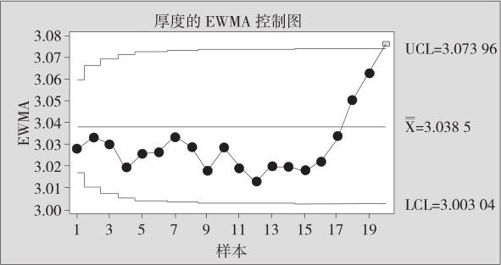
图12—13　芯片研磨厚度的EWMA控制图

EWMA控制图中，在15号样本以前生产一直正常，但从15号起均值明显地向上漂移，到了20号点已越出控制限，应判生产异常，这是常规控制图无法实现的功能。EWMA控制图对均值微小但系统的漂移有较强的判别能力。

12.4.2　标准化控制图

当过程的输出为不同规格的产品，相互之间的差别较大但样本量却较少时，使用常规控制图就显得比较牵强，且误差较大。标准化控制图应用统计方法，将各不同性质的变量都进行正态标准化，使之都化为具有近似标准正态的分布，这样一来，拥有同一背景但规格不同的几个样本组就可以放在一起进行过程评价，实现了“多品种，小批量”的产品控制。由于这种方法的基础是将所有观测值都标准化后再进行分析处理，使得控制限的数值都由标准正态分布导出，因而控制限是固定的，不需要每次都重新调整。

标准化控制图包括计数型和计量型两大类，这里仅介绍最常用的适用于计量数据的Z-MR控制图，其他控制图原理与此完全相同，在此不加赘述。在Z-MR控制图中，所绘制的统计量的计算公式如下所示，控制限的计算公式已整理成表12—11。

表12—11　标准化控制图中控制限的计算公式

当统计量计算公式中的μ和σ未定时，需要通过样本数据获得。下面用例12—7对Z-MR控制图的实际应用加以说明。

例12—7

某食品包装线共有A，B，C三种产品，现已收集到某段时间内所有产品的重量数据，试用控制图分析该过程的稳定情况（数据列在表12—12中，数据文件：SPC_ ZMR控制图.MTW）。

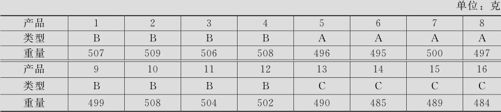
表12—12　食品重量的测量结果

解　首先，用计算机软件MINITAB绘制常规控制图I-MR：

（1）从“统计＞控制图＞单值的变量控制图＞I-MR（Stat＞Control Charts＞Variable Chartsfor Individuals＞I-MR）”进入。

（2）指定“变量（Variables）”为“重量”，运行命令后得到图12—14。

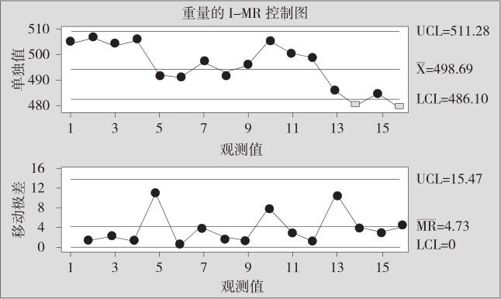
图12—14　I-MR控制图

其次，用计算机软件MINITAB实现特殊控制图Z-MR：

（1）从“统计＞控制图＞单值的变量控制图＞Z-MR（Stat＞Control Charts＞Variable Chartsfor Individuals＞Z-MR）”进入。

（2）指定“变量（Variables）”为“重量”，指定“部件编号（Part indicator）”为“类型”，运行命令后得到图12—15。

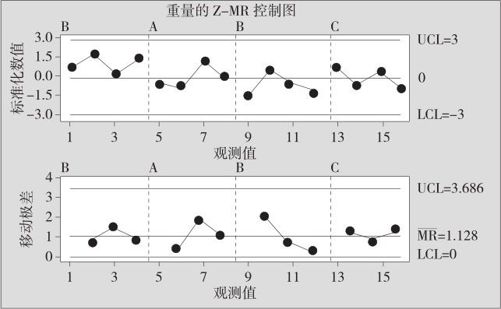
图12—15　Z-MR控制图

由以上两图的比较可知，I-MR控制图中最后3点中有2点超出控制下限，符合第1条判异准则“1点落在A区之外”，应判生产异常。但这里分析的4个数据来自产品C，并不应该与产品A，B混在一起处理。为此，分别对三种产品进行标准化，用Z-MR控制图来监控，这样将排除产品间正常的固有差异。最终可以判定生产过程一直稳定。显然，Z-MR控制图弥补了常规控制图的缺陷。当然，本例只是作为示范，样本量仍然偏少，正常情况下，每组至少应收集10个以上观测值。