12.5　非正规条件下的控制图

众所周知，控制图的理论是美国的休哈特博士建立的，他首先给出的最重要的判断就是：我们可以以μ±3σ为控制限建立控制图把特殊因素和随机因素区分开来。现在要仔细分析一下，为什么可以这样做？数据大体上应该是正态分布这个条件很是容易想到的。但实际上，控制图本来应该有三个基本的正规条件才能绘制：（1）数据相互独立；（2）数据大体是正态分布；（3）过程变异只有随机误差。严格说来，我们必须验证这三个条件都满足才能绘制控制图。如果忽略了这些条件而直接绘制控制图可能会出现很严重的问题。本节将针对这三个条件分别讨论三个问题，即：A．如果忽略这个条件将会造成什么严重后果？B．这些条件如何验证？C．出现了不满足正规条件的情况下，该如何设法解决统计过程控制问题？

对于数据非相互独立的情况，大家容易想到这个条件的重要性。例如，为了监控股市两个月内连续50天（休市时扣除计算）的交易数据是否有异常，我们是否可以直接用单值控制图进行控制？由于数据明显不是相互独立的，用50天的“平均值”作为控制图的中心线、用50天的“标准差”作为控制图的标准差，显然是不合理的，如果50天内股市有上升的趋势，势必会使前面一些数据大多会低于中心线，后面一些数据大多会高于中心线；用全部数据直接计算标准差的值也显然偏大，而导致控制限明显变宽。对于非独立数据的处理，通常要用到时间序列分析的理论，这里不再给出。有需要的读者可以参看本书参考文献［21］《基于MINITAB的现代实用统计》。但应用时间序列分析必须要求数据量相当大（至少上百组、几百组的观测值），只有这样大量的数据才能发现时间序列的规律。如果观测数据量较少，均值随组间有变化，但却又几乎是随机波动式的无任何规律性变化，则可以放弃发现规律性结果而只当作随机变化，这类数据也在一些条件下设法使用非单一变异源的情况来处理。

12.5节将分为两小节，分别讨论非正态数据的控制图和非单一变异源数据的控制图。

12.5.1　非正态数据的控制图

前几节多次提到控制图的一个前提条件：观测值服从或近似服从正态分布。因为如果数据分布非正态，原来设定的以±3σ为界来区分是否为异常原因的基本理论原则上就不成立了。然而，对不少实际工作中遇见的过程来说，它们的总体分布很可能呈现出非正态分布，如正偏、负偏等不对称形态。这里要说明的是，即使监控平均值，也不能认为有“中心极限定理”保证近似正态，那要子组样本量相当大才行，而控制图中子组样本量大多不超过10，这是很难肯定近似为正态分布的。一方面控制图要求数据基本正态，否则控制图没意义；另一方面，数据又确实非正态，那该如何处理呢？实践证明：对数据作变换会改变分布的类型，也就是说，通过适当的变换可使非正态分布转化为正态分布。常见的转换方法有：y＝lny，y＝y^－1，y＝y²，y＝等，它们可能将转换后的数据分布近似拟合为中间高、两边低、左右对称的钟形曲线。比较规范和通用的做法是运用Box-Cox法进行转换。

Box-Cox法的基本思路是首先选择一个合适的λ值，然后带入下列转换公式，将原来随机变量y变换成新的随机变量：

最终得到服从正态或近似正态分布的随机变量y^*。

下面用例12—8对非正态数据绘制控制图的实际应用加以示范。

例12—8

在某化工生产过程中发现，当催化剂接近耗尽时，表示杂质含量的数据呈偏态分布，试用正确的方法绘制控制图（数据列在表12—13中，数据文件：SPC_Box Cox变换.MTW）。

表12—13　杂质含量的测量结果

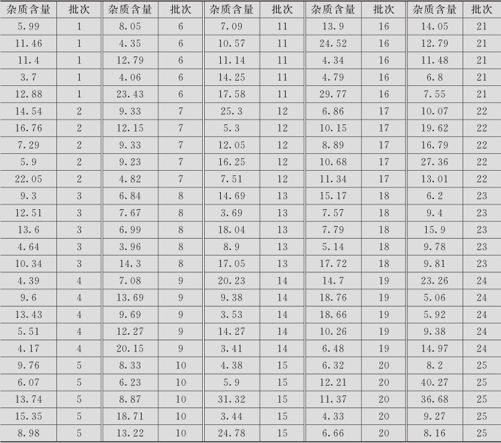
解　计算机软件MINITAB的实现方法如下：

1．确认非正态性。

首先，对数据进行正态性检验：从“统计＞基本统计量＞正态性检验（Stat＞Basic Statistics＞Normality test）”进入，指定“变量（Variables）”为“杂质含量”，运行命令后得到图12—16。

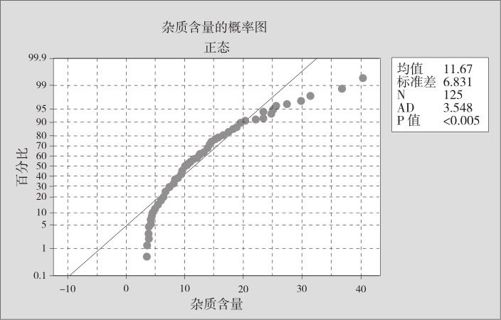
图12—16　原始数据的正态性检验

由图12—16可知p值＜0.005，确认数据为非正态分布，所以要进行Box-Cox变换。

2．选择Box-Cox变换中的参数Lambda（λ）。

从“统计＞控制图＞Box-Cox变换（Stat＞Control Charts＞Box-Cox Transformation）”进入，指定“图表的所有观测值均在一列中（All observations for a chart are in one column）”为“杂质含量”，指定“子组大小（Subgroup size）”为“5”，得到图12—17。

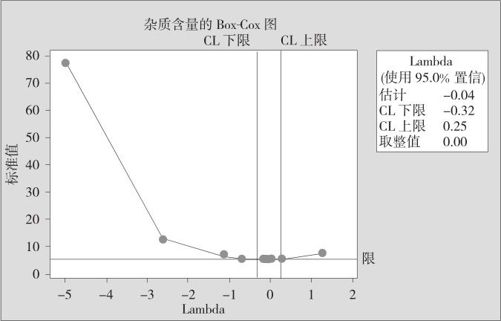
图12—17　Box-Cox转换

由图12—17可知Lambda（λ）的估计最佳值为－0.04。其实不必这样严格要求，取Lambda（λ）落入图12—17中右上部列出的CL下限与CL上限之间就可以了，为了让转换更简单，可以将Lambda（λ）值调整为0.00。

3．将原始数据进行变换并存储。

按照式（12—4）中y＝lny的计算公式进行数据转换，并将转换好的数据y存储在名为“新数据”的新一列中。此时，为了更保险，应再次对变换后的数据进行正态性检验（见图12—18）。

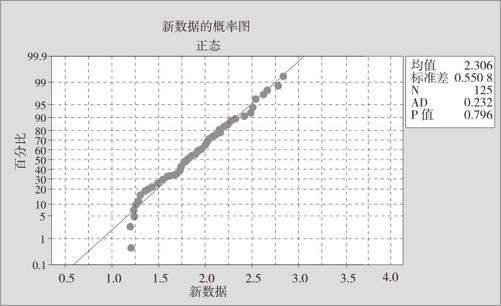
图12—18　转换后数据的正态性检验

由图12—18可知p值＝0.796，显然，数据被成功转换为正态分布。

4．对于变换后的数据绘制均值—极差控制图。

从“统计＞控制图＞子组的变量控制图＞Xbar-R（Stat＞Control Charts＞Variable Chartsfor Subgroups＞Xbar-R）”进入，指定“图表的所有观测值均在一列中（Al obser-vationsforachartareinonecolumn）”为“新数据”，指定“子组大小（Subgroup size）”为“5”，在“Xbar-R选项＞估计＞‘子组大小＞1’（Xbar-ROptions＞Estimate＞‘Sub-group Size＞1’）”中选择“Rbar”，运行命令后得到图12—19。

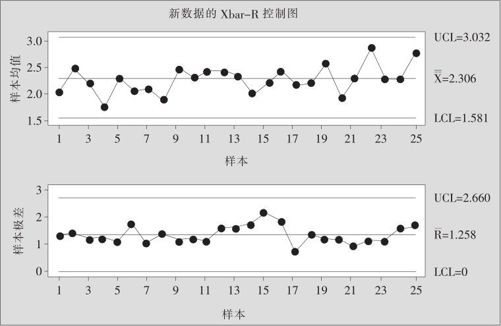
图12—19　对变换后数据绘制的Xbar-R控制图

5．将控制图绘制在原变量趋势图内。

如果要对过程进行实时监控，只得到图12—19是不够的，我们希望在原数据的趋势图内加上控制限。为此，要把图12—19中的各控制限经“反变换”再变回为原始变量的界限。由于变换后的波动性质有很大变化，对于非正态数据通常只绘制Xbar图而略去R图。

经计算，e^3.032＝20.73，e^2.306＝10.03，e^1.581＝4.859，这就是各控制限。在绘图前，先应将数据分组求出平均值：从“统计＞基本统计量＞存储描述性统计（Stat＞Basic Statistic＞Storage Descriptive Statistics）”进入，指定“变量（Variable）”为“杂质含量”，指定“按变量（By Variable）”为“批次”，在“统计量（Statistics）”中选择“均值（Mean）”，运行命令后得到数据表中的C3～C5。再对平均值这列绘制“时间序列图（Time Series Plot）”就可以了。具体操作是：从“图形＞时间序列图＞简单（Graph＞Time Series Plot＞Simple）”进入，指定“序列（Series）”为“平均值”，并在“时间／尺度（Time/Scale）”中，打开“参考线（Reference Line）”后，将上述三个控制限值依次输入“显示Y值的参考线（Display YReference Line）”中，运行命令后得到图12—20。这样的图就可以在实际工作中使用了。

图12—20　对原始数据绘制的Xbar控制图

在使用MINITAB软件直接对非正态数据绘制控制图时，其实可以省略上述步骤中的第3步。实际上，在第4步中计算变换后数据的控制限时，只要确知λ的数值则可以直接从原始数据获得。其操作是：从“统计＞控制图＞子组的变量控制图＞Xbar-R（Stat＞Control Charts＞Variable Chartsfor Subgroups＞Xbar-R）”进入，指定数据列后，打开“Xbar-R选项（Xbar-ROptions）”窗，再从其中打开“Box-Cox”窗，指定Lambda（λ）的值，则计算机在计算后直接可以显示出图12—19的结果。这将节省求数据变换后结果的步骤。

如果数据无法经过Box-Cox变换化为正态分布又如何绘制控制图呢？其实通过仔细分析可以看出，所谓控制图其实就是找出一个区间范围，使得绝大部分数据落入此区间，因而一旦有数据落在此区间之外则可以认为出现了异常。因此，我们可以不必追究数据分布的准确类型，只要能找出这样的范围就行了。针对具体的数据，我们可以通过非参数的数值方法直接求得其分位数，例如0.5％，50％及99.5％三个分位数，它们可以被当作控制图中的下、中、上三条控制限（LCL，CL，UCL）画入图中。这时，包含在LCL，UCL之间部分的数据将达到99％，因而可以起到控制图的作用。

这里自然有个问题，为什么不与正态分布完全相同地取99.73％作为控制范围呢？事实上，利用数据直接计算分位数（尤其是小分位数）是有一定条件的。一般说来，计算p分位数（p很小），则样本量n要满足

具体说来，对于p＝0.005，n要超过100才行；如果要像正态分布那样，p＝0.00135，则n要超过370才行。一般情况下的样本量不可能有这样大，因此，通常还是选用0.5％，50％及99.5％三个分位数作为控制图中的下、中、上三条控制限。

调用宏指令UCLC可以直接得到上述结果，只要在宏指令UCLC后指定数据存放的变量名就行了。具体到例12—8，由于按组计算的数据只有25个，为了演示非参数方法的控制图计算方法，我们把题目改为绘制单值控制图。由于其数据存放于C1中，因此宏指令调用格式是：

％UCLC　C1

计算机运算后可得下列结果：

结果：SPC_Box COX变换.MTW

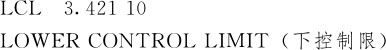
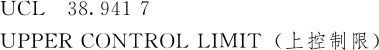
由于这里的控制限结果是对单值给出的，因此不能将这些结果与图12—20中的结果直接比较。如果对于例12—8也按单值控制图计算，同样选择Box-Cox变换中的参数λ＝0，则三个控制限值分别为：0.651，2.306及3.962；经计算，e^0.651＝1.917，e^2.306＝10.03，e^3.962＝52.562，这就是最终各控制限。而一般说来，用非参数方法得到的控制范围要比用Box-Cox变换法得到的范围稍窄些，这是因为，毕竟包含数据99％的范围要比包含数据99.73％的范围稍窄些，但这并不影响控制图的正常使用。

12.5.2　非单一变异源数据的控制图

我们先看一个例题。

例12—9

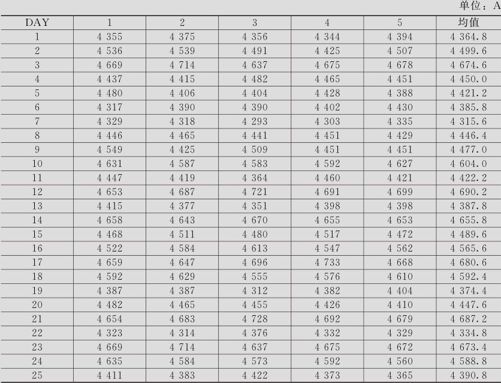
为芯片镀膜的车间，在连续25天内，每天抽取5片芯片，测量其镀膜厚度，其测量结果如下（见表12—14镀膜厚度数据，数据文件：SPC_芯片镀膜.MTW）。绘制控制图以判断生产是否正常。

表12—14　镀膜厚度数据

解　带子组的控制图可以有两种绘制方法。一种是先求出每组（本例是天）的均值，然后对均值绘制I-MR（单值—移动极差）控制图；另一种是直接使用原始数据，绘制Xbar-R（均值—极差）控制图。

绘制I-MR图的方法是先求出子组均值，将其存入某列（本例是放在C5中），然后再绘制控制图。计算机软件MINITAB的实现方法如下：

1．从“统计＞控制图＞单值的变量控制图＞I-MR（Stat＞Control Charts＞Variable Chartsfor Individual＞I-MR）”进入。

2．指定“变量（Variables）”为“均值1”。

3．在“统计＞控制图＞单值变量控制图＞I-MR＞I-MR选项＞检验（Stat＞Control Charts＞Variable Charts for Individual＞I-MR＞I-MR Options＞Tests）”中，可以逐一看到根据前文所述的SPC中8项判异准则的判异检验。

4．运行命令后得到图12—21。

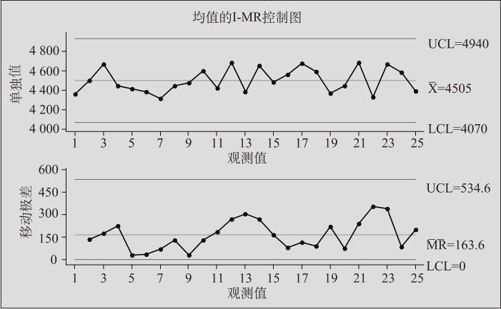
图12—21　芯片镀膜均值绘制的I-MR控制图

从图12—21看，生产一切都正常，8项判异检验无一异常。

下面直接用原始数据，绘制Xbar-R（均值－极差）控制图。其操作方法与例12—1完全相同，这里不再重复。运行命令后得到图12—22。

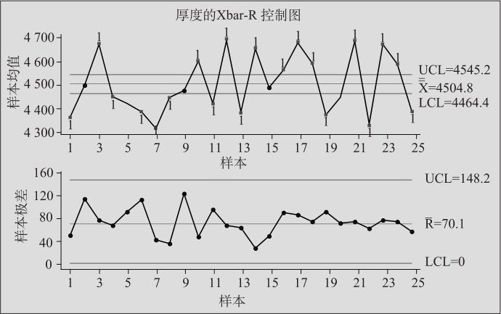
图12—22　芯片镀膜原始数据绘制的Xbar-R控制图

从图中可以看出，25天的极差都在控制限内，说明每天的波动状况是受控的；但对于均值，则除个别天之外，绝大多数点都落在控制限外，说明芯片镀膜生产过程的均值严重不受控。

用两种绘制控制图的方法所得结论怎么会这样完全不同？

仔细分析这两张图可以看出，它们的均值都是相同的，其不同出现在对于标准差的估计上。容易看出，Xbar-R控制图中，是用各小组内的极差（除以极差系数d₂）来估计总体的标准差的；均值的I-MR控制图中，是用各组间的移动极差（除以极差系数d₂＝1.128）来估计总体的标准差的。前者使用的是组内差，后者使用的是组间差。如果生产过程数据只有唯一的变异来源，所有数据的波动都来自随机误差的话，二者的估计应该大体相同；但如果生产过程数据不只有唯一的变异来源，数据的波动一方面来自随机误差（根据合理子组的原理，组内差反映的就是随机误差），另一方面还来自组间可能有的波动，这样一来，用组间移动极差估计出来的标准差会比仅用组内差（不考虑组间差）估计出来的标准差大很多，这必将导致I-MR控制限会比Xbar-R控制限宽很多，因此才会使“I-MR图判断认为过程均值正常”，而“Xbar-R图判断认为过程均值几乎点点都不正常”。

下面我们先讨论如何判断收集到的数据中波动全部来自随机波动？换言之，如何分析数据的变异源是如何组成的？在什么条件下达到什么标准就可以认为数据中波动全部来自随机波动？

这就牵涉到我们曾经在第10章所学的变异源分析方法。

我们先用多变异图来直观描述一下例12—9的状况。绘制多变异图的方法已在例10—1（见图10—2、图10—3、图10—4）中给出。图12—23是例12—9的多变异图。

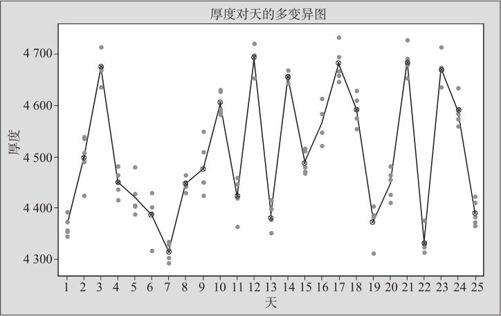
图12—23　芯片镀膜原始数据绘制的多变异图

从图12—23可以看出，各天内5片芯片厚度的波动都不大，但天与天间的均值相差较大。

下面我们给出变异源的定量分析。例12—9中实际上只有一个因子，与例10—4的定量分析方法完全相同。其方差分量计算结果如下：

方差分量

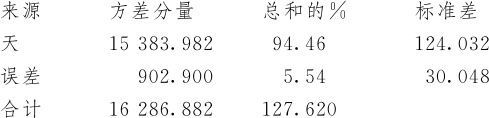
从计算结果可以看出，在芯片镀膜数据中，组内差（误差）方差分量为902.900，只占总变异的5.54％；组间差（天）方差分量为15383.982，占总变异的94.46％。这里不但不能说“随机误差为唯一变异源”，实际上组间差反而比组内差要大很多，组间差形成的波动占了主导地位。此例当然是非常特殊的案例，一般情况下不会如此严重。通常认为，随机误差的方差分量超过90％以上时，可以认为随机误差为唯一变异源。

如果不能认为随机误差为唯一变异源时，或是发现数据不独立时（这时对标准差不同的估计方法将导致结果相差悬殊），该如何进行过程统计控制？按休哈特博士最初的思想，这种情况下是不能够绘制控制图的。但是再深入分析一下控制图的基本思想，它主要是监控生产过程是否稳定的。如果“随机误差不是唯一的变异源”的状况虽然不好，但它一直不随时间而改变，这是否也应该认为是稳定的呢？应该也认为是稳定的。这样一来，我们就应该放宽生成控制图的条件，允许生产过程中包含不止一个变异源，而对各个变异源的状况分别予以监控。这时，如果组间差一直很大，各组均值间可能有较大波动，但这种状况能保持稳定不变，则也应该认为是正常的。为此，我们就用组均值及其移动极差作为控制图的主体，同时再增加对组内差的监控，绘制各组的极差（或标准差）控制图，这就比较全面了。同样，如果数据有非独立的情况，综合上面这些要求，这就形成了“I-MR-R（S）组内／组间”控制图，在MINITAB控制图内有专门的窗口来完成此功能。具体操作如下：

从“统计＞控制图＞子组的变量控制图＞I-MR-R（S）（组间／组内）（Stat＞Control Charts＞Variable Chartsfor Subgroup＞I-MR-R（S））”进入。在表上方选择“图表的所有观测值均在一列中”（数据位于多列中则选“子组的观测值位于多列的同一行中”），在输入窗口中填写变量名“厚度”，在“子组大小（Subgroup size）”填写“5”。运行命令后可得如图12—24所示结果。

从图12—24中可以看出，I-MR-R/S控制图是由三张图组成的（以前最多只有两张图），其中，上图和中图其实就是图12—21中的两张图，下图其实就是图12—22中的下面那张组内极差控制图。读图时，先看组内极差控制图，如果没有异常，说明各组内的波动状况是正常的；如果有异常，先要找到该组异常的原因。图12—24中的组内极差控制图完全正常。在分析极差控制图后，再来看组间的单值—移动极差控制图，看图中是否有异常的组。图12—24中的单值－移动极差控制图也是正常的。这说明，芯片镀膜生产过程厚度虽然有较严重的组间波动，但总体上看还是稳定的。

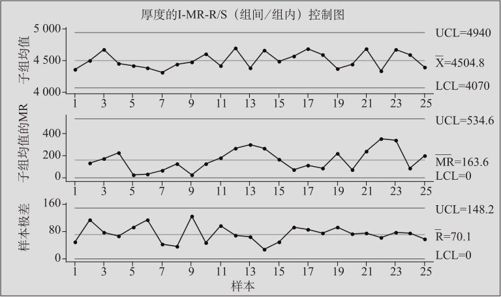
图12—24　芯片镀膜数据绘制的I-MR-R/S控制图

我们再看另一个例子。

例12—10

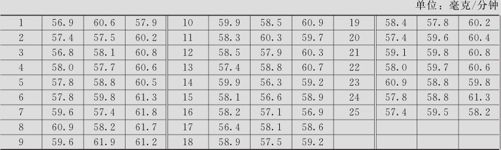
汽车尾气浓度问题。为达到环保目标，现检测M运输公司所属汽车队的汽车尾气浓度。每天随机抽取3辆汽车，连续25天检测其尾气含颗粒物浓度值。其测量结果如下（见表12—15汽车尾气浓度数据，数据文件：SPC_尾气浓度.MTW）。

表12—15　汽车尾气浓度数据

我们先对25天数据绘制均值－极差控制图（操作方法与例12—1完全相同），得到控制图如图12—25所示。

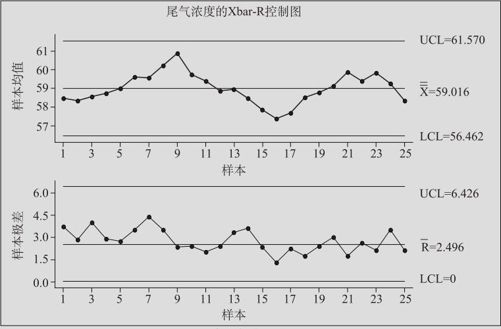
图12—25　汽车尾气浓度的Xbar-R控制图

从图12—25可以看出，汽车尾气浓度数据是受控的，一切都正常。

下面我们先求出每天3辆汽车尾气浓度的均值，对于这25个均值绘制单值—移动极差控制图（方法与例12—9完全相同），结果见图12—26。

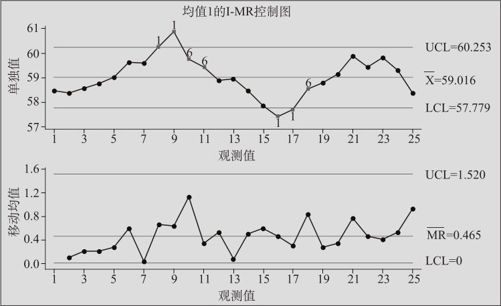
图12—26　汽车尾气浓度均值的I-MR控制图

从图12—26可以看出，移动极差控制图是正常的，而单值图中，8，9号超出上限，16，17号超出下限，10，11，18也不正常，应该判为均值异常。

这里又出现了两张图结论不同的情况，但例12—10与例12—9情况相反，例12—10是均值—极差图正常，单值—移动极差图反而不正常。例12—9是单值—移动极差图正常，均值—极差图不正常。

我们再次提出问题：用两种绘制控制图的方法所得结论怎么会这样完全不同？

在例12—10中，情况与例12—9是不同的。在图12—25的上图（均值控制图）中，明显看到均值有连续漂移的情况，先是上升再下降，然后再次上升再下降，天与天之间明显不独立，每个数据都强烈依赖于前一个数据的状况，高值接着是高值；低值接着是低值，这样就会导致移动极差偏小。这样一来，用组间移动极差估计出来的标准差会比用组内差估计出来的标准差小很多，这必将导致I-MR控制限会比Xbar-R控制限窄很多，因此才会使“Xbar-R图判断认为过程均值正常”，而“I-MR图判断认为过程均值有些点不正常”。

对于例12—10，我们可以同样绘制I-MR-R/S图，结果见图12—27。

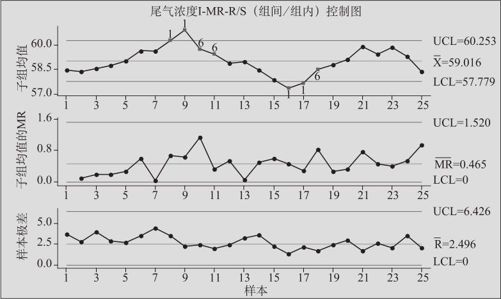
图12—27　汽车尾气浓度的I-MR-R/S控制图

从图12—27的下图中可以看出，各子组的极差基本是正常的；但从其上图（单值控制图）中看出有好多点不正常。

如何分析均值序列是否可以看出是独立的？在例12—10中，由于图12—26中日均值有明显的相依状况，对于日均值，应该进行数据的独立性检验—游程检验（见例5—5）。要注意的是独立性检验不一定先要求出均值列来，我们可以直接对带子组的数据直接绘制运行图进行游程检验，再求出游程总个数，而这只要从“统计＞质量工具＞运行图（Stat＞Quality Tools＞Run Chart）”入口，选定“子组大小（Subgroup sizes）”为“3”，即可以直接进行游程检验。结果见图12—28。

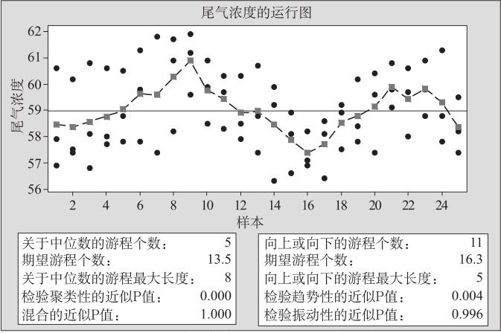
图12—28　汽车尾气浓度的运行图（为游程检验用）

对于25组数据，却只有5个游程，经过游程检验（详细方法见例5—5），查附表10，可知游程个数的双侧检验的下限为8，因此应该拒绝“数据独立”的原假设，判定数据是不独立的。

对于非独立的序列不能再采用普通的均值—极差控制图来进行控制，必须换成I-MR-R/S控制图，考虑其均值序列的可控性。对于本例而言，应该判定均值序列有失控的现象。当然，严格说来，均值非独立的序列究竟该如何判断其稳定性？坚持用水平的中心线作为控制图中心，是在数据完全独立时的标准办法；如果对于有系统漂移的很强的正自相关的序列可以用“单参数指数光滑法”求出其光滑曲线，然后以此曲线为控制图中心，以残差作为控制对象，这将是时间序列分析中控制图的研究方法。详细内容可参看本书文献［21］《基于MINITAB的现代实用统计》第14章。这时对于时间序列的稳定性将比现在有更宽的理解。

总之，如果数据是完全独立的，而且所有变异都只是由于随机误差构成的，则用组间移动极差估计出来的标准差和用组内差估计出来的标准差相差不大，普通的常规控制图就可以解决控制问题；但如果数据的变异源不单是随机误差，还混有组间差（组间有较大的波动），或是组间有强烈的相依，移动极差会非常小，则必须另外专门考虑子组均值是否受控。

下面归纳I-MR-R/S控制图的适用条件。

I-MR-R/S控制图提供了三个控制图的组合，这将提供一种评估过程位置的稳定性、变异的组内差、组间差的各分量的方法。

不论数据组间差的变异是由规律性的时间序列生成的，还是完全由随机波动形成的，只要其变动波动只与某一个（不能是两个或更多）原因有关，我们就可以将其作为组间差。换言之，如果变异源只有两部分：随机误差和另一个变异原因，则可以使用I-MR-R/S控制图来监控过程的统计稳定性。详细说来，如果随机误差方差分量大于总方差的90％，且均值序列可以看成是独立的，则可以使用简单的常规控制图来处理；如果随机误差方差分量小于总方差的90％（即另一变异源形成的方差分量超过总方差的10％），或均值序列不可以看成是独立的，则应该使用I-MR-R/S控制图来处理；如果数据是独立的，但变异源除了随机误差外还至少有两个以上变异源，虽然从理论上讲，应该可以对每一个变异源加以控制，但实际上则无法使用计算机控制图来监控过程，必须减少变异源到恰好只有两个变异源（组内、组间）才能使用I-MR-R/S控制图实现过程的统计控制。如果数据本身有明显的不独立性，那么我们绘制常用控制图的基本条件都不能满足，这时控制图就不一定是适用的，所有的结论都应该存疑，这是我们在使用控制图时必须要小心的。