14.3　仿　真

仿真（simulation），也称模拟，是建立系统或决策问题的数学模型或者逻辑模型，并以该模型进行试验，以获得对系统行为的认识或者帮助解决决策问题的过程。常用的仿真方法也称为蒙特卡罗方法，其起源最早可以追溯到18世纪下半期的蒲丰试验，20世纪80年代电子计算机的应用使它得以广泛应用，操作也越来越简单。

建模的形式很多，可以根据已知的自然定理建立数学关系模型（如万有引力模型），可以根据历史数据建立回归模型，可以根据试验设计观察的结果建立对应模型，还可以根据常识建立商业流程及产品的模型，等等。

执行仿真方法，一般需要遵循下列四个基本步骤：

（1）针对实际问题建立一个简单且便于实现的概率统计模型，使所得的结果恰好是所建模型的概率分布或某个数字特征。

（2）对模型中的随机变量建立抽样方法，在计算机上进行仿真试验，抽取足够的随机数，并对有关的事件进行统计。

（3）对模拟试验结果进行统计描述和分析，如平均值、标准差和拟合概率分布等。

（4）必要时还应改进模型以降低估计方差和减少试验费用，提高模拟计算的效率。

采用仿真方法的优点有：

（1）分析人员无须建立或实际完成拟议中的系统或决策就能够评价模型，或者在不干扰现有系统的情况下对模型进行试验。

（2）一般比许多其他分析方法更容易理解。

（3）为任意假设建立模型的能力显然使仿真不必顾及其他管理科学方法，当分析模型不合适或者不存在的时候，这一点尤为重要。

当然，目前的仿真技术还存在局限性：

（1）必须获得输入的数据、开发仿真的模型和计算机程序，以及解释结果，有时为此需要花费大量时间。

（2）没有精确的答案。

下面将结合一个典型的服务流程设计案例，介绍仿真的基本原理和MINITAB的实现方法。

例14—3

某银行从“客户之声”的调查得知，95％以上的顾客代表希望完成整个贷款流程所需的时间能够控制在136个工作小时之内。一般而言，整个贷款流程可分为六大步骤（见图14—19），总体周期时间等于六项步骤周期时间之和。研发部门根据此要求新近开发了一个房贷产品，以改进以往的工作方法。结合贷款工作的本身特征，设定新产品每个步骤的周期时间分别遵循不同的分布规律，如表14—2所示。试从总体周期时间的角度判断新产品的流程能力如何，能否满足顾客对及时性的要求。

图14—19　贷款流程

表14—2　周期时间的设定

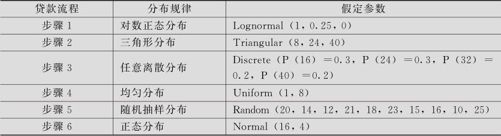
不言而喻，该案例很适合先用仿真产生数据源，再用过程能力指数的计算方法进行分析。下面介绍用MINITAB实现的具体方法。

（1）根据步骤3和步骤5的时间分布特点，制作一个备用数据表，形式如图14—20所示。

图14—20　仿真分析备用数据表

（2）为仿真步骤1的周期时间，从“计算＞随机数据＞对数正态（Calc＞Random data＞Lognormal）”进入。指定“要生成的数据行数（Number of rows of data to generate）”为“1000”，指定“存储于列（Store in column（s））”为“步骤1”，指定“位置（Location）”为“1”，指定“尺度（Scale）”为“0.25”，指定“阈值（Threshold）”为“0”，运行命令后得到新的一列“步骤1”。

（3）为仿真步骤2的周期时间，从“计算＞随机数据＞三角形（Calc＞Random Data＞Triangular）”进入。指定“要生成的数据行数（Number of rows of data to generate）”为“1000”，指定“存储于列（Store in column（s））”为“步骤2”，指定“下端点（Lower endpoint）”为“8”，指定“众数（Mode）”为“24”，指定“上端点（Upperend-point）”为“40”，运行命令后得到新的一列“步骤2”。

（4）为仿真步骤3的周期时间，从“计算＞随机数据＞任意离散（Calc＞Random Data＞Discrete）”进入。指定“要生成的数据行数（Number of rows of data to generate）”为“1000”，指定“存储于列（Store in column（s））”为“步骤3”，指定“值在（Valuesin）”为“审核时间”，指定“概率在（Probabilities in）”为“概率”，运行命令后得到新的一列“步骤3”。

（5）为仿真步骤4的周期时间，从“计算＞随机数据＞均匀（Calc＞Random Data＞Uniform）”进入。指定“要生成的数据行数（Number of rows of data to generate）”为“1000”，指定“存储于列（Store in column（s））”为“步骤4”，指定“下端点（Lowerendpoint）”为“1”，指定“上端点（Upper endpoint）”为“8”，运行命令后得到新的一列“步骤4”。

（6）为仿真步骤5的周期时间，从“计算＞随机数据＞来自列的样本（Calc＞Random Data＞Sample From Columns）”进入。指定“取样行号（Number of rows to sample）”为“1000”，指定“来自列（From column）”为“完成时间”，指定“存储于列（Store in column（s））”为“步骤5”，选择“重置取样（Sample with replacement）”，运行命令后得到新的一列“步骤5”。

（7）为仿真步骤6的周期时间，从“计算＞随机数据＞正态（Calc＞Random Data＞Normal）”进入。指定“要生成的数据行数（Number of rows of data to generate）”为“1000”，指定“存储于列（Store in column（s））”为“步骤6”，指定“均值（Mean）”为“16”，指定“标准差（Standard Deviation）”为“4”，运行命令后得到新的一列“步骤6”。

（8）为计算总体周期时间，从“计算＞计算器（Calc＞Calculator）”进入。指定“将结果存储在（Store result in variable）”为“总体周期时间”，在“表达式（Expression）”中输入“步骤1＋步骤2＋步骤3＋步骤4＋步骤5＋步骤6”，选择“设置为公式（Setasformula）”，运行命令后得到新的一列“总体周期时间”。

至此，可以得到仿真并汇总后的数据表，摘选1000行数据中的前10行，如图14—21所示。注意：这里的数据是随机产生的，读者产生的数据当然不一定如图14—21所示。另外，由于数据的随机性将导致仿真得到的结果具有不确定性，例如有时仿真模拟得到的数据不能认为是服从正态分布等。仿真也常常要进行多次，以增加其可信度。

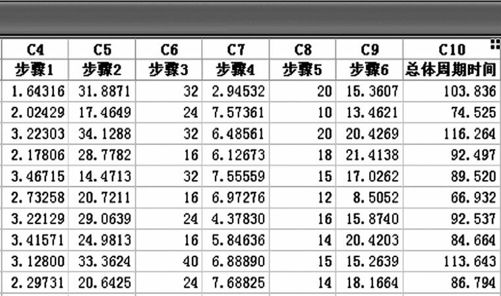
图14—21　仿真并汇总后的数据表

（9）为检验数据的正态性，从“统计＞基本统计量＞正态性检验（Stat＞Basic Statistics＞Normality test）”进入。指定“变量（Variables）”为“总体周期时间”，运行命令后得到图14—22，由于p＝0.112＞0.05，可以认为数据服从正态分布。

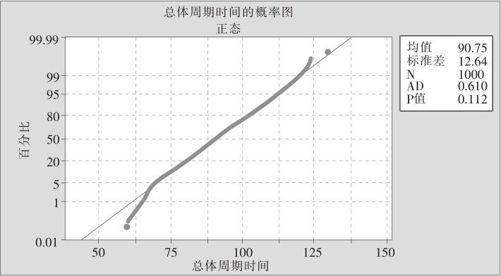
图14—22　总体周期时间的正态性检验

（10）为计算过程能力指数，从“统计＞质量工具＞能力分析＞正态（Stat＞Quality Tools＞Capability Analysis＞Normal）”进入。指定“单列（Single column）”为“总体周期时间”，指定“样本大小（Subgroup size）”为“1”，在“规格上限（Upper spec）”中输入“136”，运行命令后得到图14—23。

图14—23　总体周期时间的过程能力分析

由图14—23可知，C_pk＝1.19＞1，说明过程能力较好，能够满足大部分顾客对总体周期时间的要求。当然，离六西格玛的目标还有一定的距离。这里要注意的是：由于仿真数据产生的随机特性，每次操作的计算结果都可能有一定差别，这是正常的波动。

越来越多的企业和研究单位认识到商业仿真的重要性和实施商业仿真的迫切性。从长远看来，仿真必然会被越来越多的企业和单位所接受，成为决策者和研究者分析的利器。