9.1　相关分析

这里通过一个例题来详细了解相关分析的具体内容。

例9—1

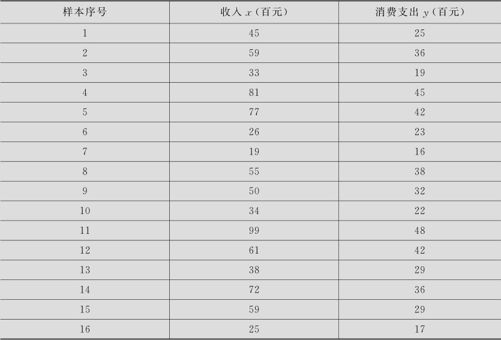
某市场分析员进行了一项研究，分析某地区居民的每月家庭消费支出y与每月家庭收入x之间的关系。现从该地区随机抽取了16个家庭组成一个样本，数据见表9—1（数据文件：REG_收入与支出.MTW）。试判定：该地区居民的每月家庭消费支出y与每月家庭收入x是否相关？如果相关，那么相关是否密切？在显著性水平α＝0.05时，给出y与x的一元线性回归方程，判定方程是否有效。当家庭收入为8000元时，预测消费支出y的大致范围。

表9—1　某地区居民每月家庭收入与消费支出数据记录

这里首先要解决的问题是：收入x和消费支出y相关吗？经验告诉我们似乎是相关的，但统计学不相信表象，我们要用统计的方法证实它们确实相关。

我们的做法是：

（1）先绘制x，y的散点图。通过散点图形的特点大致可以了解x，y是否可能存在相关关系。打开数据文件“REG_收入与支出.MTW”，在MINITAB中，选择指令“图形＞散点图（Graph＞Scatter plot）”，输入变量后，得到图9—1。

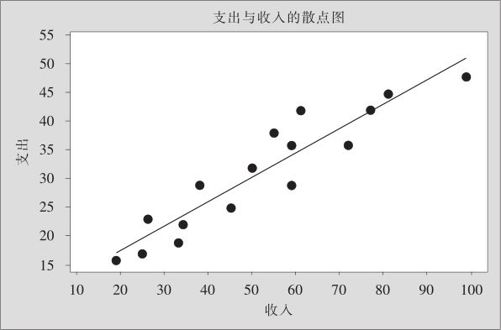
图9—1　消费支出与收入散点图

分析散点图大致有以下特点：

●由图9—1可以看出，本例中两个变量间确实相关，当收入x增加时，消费支出y也呈上升趋势。

●存在一条上升的直线，大致使得：1）点密集分布在这条直线的两侧；2）两侧点的分布数目大体相等；3）点在直线两侧分布的具体位置完全是随机的。

（2）为了更为准确地描述x，y相关的密切程度，我们引入一个统计量来量化它，这就是样本相关系数r。

设（x₁，y₁），…，（x_n，y_n）为抽样得到的来自两个总体的配对随机样本数据，T_x，T_y分别代表所有x和所有y数据之和，L_xy为x，y的离差乘积和；L_xx，L_yy分别为x，y的离差平方和。相关系数定义为：

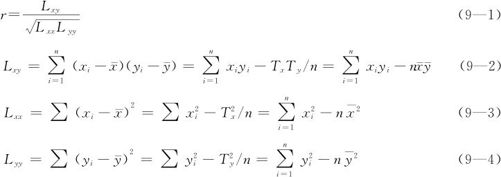
回到例9—1，将数据代入式（9—1）至式（9—4），计算后可以得到：

L_xy＝3259.81，L_xx＝7690.94，L_yy＝1580.44

所以

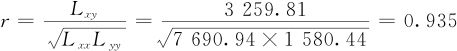
从理论上来说，根据r的计算公式，数学推导可以证明：|r|≤1。对于应用工作者来说，关键是要理解相关系数的含义。

相关系数r在不同取值范围时与散点图的关系大致如图9—2、图9—3、图9—4所示：

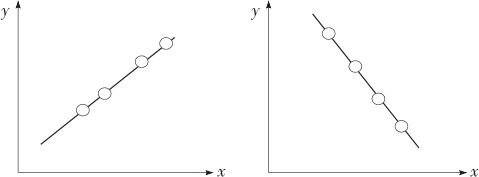
图9—2　r＝±1时，x，y完全线性相关散点图

图9—3　|r|＜＜1时，x，y线性相关散点图

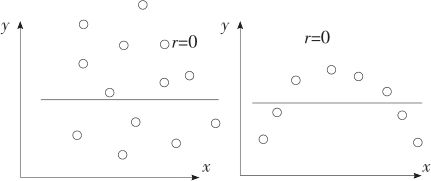
图9—4　r＝0时，x，y散点图

从相关系数的定义及从上述4张图上可以看出，r的绝对值越接近于1，则数据点与直线越靠拢；r的绝对值越小，则数据点与直线越远离。直到最后，如果x与y完全无关，则r应该接近于0；但反之，如果r接近于0，我们不能断言“x与y完全无关”，实际上，x与y的关系很可能如图9—4中右图那样，是有二次函数关系的。因此，正确的说法是：如果r接近于0，我们可以断言x与y非线性相关。总之，相关系数r是两个变量间线性相关关系密切程度的度量。

（3）在工程实际中，如果知道某两个变量间没有线性相关关系，那么它们总体的相关系数应该为0，但实际上由于实验或测量的误差，我们根据样本数据计算出来的相关系数却不会准确等于0。自然地，我们会想到：到底样本相关系数r为多大时，才可以认为x，y是在统计意义上具有线性相关关系呢？

有的六西格玛管理教材中说“只要相关系数绝对值大于0.8，则二者肯定相关”，这显然是错误的。原因就在于样本相关系数r的分布与样本量密切相关，我们需要通过如下假设检验的方式加以判断。

（1）设立假设：假定变量间总体相关系数为ρ，则

（2）确定检验统计量及在原假设成立条件下的分布。由于得知近似有

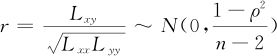
这里ρ是总体相关系数，是个未知的参数，用样本相关系数r作为ρ的估计量，并对r进行标准化变换，可以得知在原假设成立条件下近似有下列结论：

（3）对应前面三组假设检验问题式（9—5），拒绝域W分别为：

H₁：ρ＞0，W：{t＞t_1－α（n－2）}，若落入拒绝域，可以断言两变量间正线性相关；

H₁：ρ＜0，W：{t＜t_α（n－2）}，若落入拒绝域，可以断言两变量间负线性相关；

H₁：ρ≠0，W：{|t|＞t_1－α/2（n－2）}，若落入拒绝域，可以断言两变量间线性相关。

回到例9—1，我们来判定x，y是否线性相关。

我们设定的假设是：H₀：ρ＝0，H₁：ρ≠0。

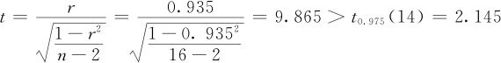
所以，结论是拒绝原假设，x，y是线性相关的。

对于相关系数的检验也可以直接通过查表的方式进行。

对于检验H₀：ρ＝0，H₁：ρ≠0，在本书附表12中给出了|r|的临界值r_α。如果实际计算所得到的|r|＞r_α，则拒绝原假设。例如，对于例9—1，当n－2＝14时，取α＝0.05，查附表12得临界值是0.4973，由于0.935＞0.4973，因此拒绝H₀，即可以断言x，y是线性相关的。

如果用MINITAB来判定，会简单得多，打开数据文件“REG_收入与支出.MTW”，选择指令“统计＞基本统计量＞相关（Stat＞Basic Statistics＞Correlation）”，如图9—5所示；输入变量后，得到以下结果：

图9—5　相关性检验操作图

相关：支出，收入

支出和收入的Pearson相关系数＝0.935

P值＝0.000

可以看到，输出的相关系数r＝0.935，与手算结果是一致的，另外输出结果中p值＝0＜0.05。所以，结论是拒绝原假设，收入x与消费支出y是线性相关的。

要注意的是：x与y显著相关并不意味着x与y间一定存在因果关系，可能它们都以另一个变量为原因。例如，对于一个城市，“当日雨伞的销售量”与“当日道路上交通事故量”高度相关，但二者谁也不是另者的原因，实际上二者都以“当日降雨情况”为原因。因此在六西格玛管理中，寻找原因时不能只看相关系数，还要分析变量间关系的结构；但反过来说，寻找y的原因时，只可能在与y有显著密切相关关系的变量组中寻找；与y关系不密切者更不可能是y的原因。因此，研究相关关系对于六西格玛管理而言还是很重要的。

用上述求相关系数的方法，可以同时求出多个变量间的相关系数矩阵。例如，在本章9.3节中介绍一个例子，研究水泥在凝固时放出的热量y（卡／克）与水泥中4种化学成分物质x₁，x₂，x₃，x₄的关系。共记录了13组数据，列在表9—8中（数据文件“REG_Hald数据.MTW”）。现在希望判断水泥的4种化学成分间是否有相关关系。这是个同时讨论多个自变量间关系是否密切相关的实例。

先画图来直观观察一下。由于变量个数大于2，因此散点图就不够用了。我们用矩阵图（matrix plot）更方便。从指令“图形＞矩阵图（Graph＞Matrix Plot）”入口，在填写变量时，将x₁，x₂，x₃，x₄都输入作为变量，得到如图9—6所示图形。

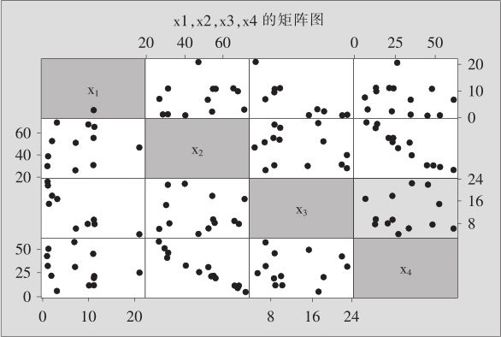
图9—6　多变量的矩阵图

从图中可以看出x₁与x₃，x₂与x₄之间有负相关的迹象，但它们是否真的相关呢？我们来计算它们之间的相关系数。

从指令“统计＞基本统计量＞相关（Stat＞Basic Statistics＞Correlation）”入口，在填写变量时，将x₁，x₂，x₃，x₄都输入作为变量，得到以下结果：

结果：REG_Hald数据.MTW

相关：x1，x2，x3，x4

单元格内容：Pearson相关系数

P值

从输出结果中可以看出，x₁与x₃的相关系数r＝-0.824，p值＝0.001＜0.05；x₂与x₄的相关系数r＝-0.973，p值＝0＜0.05；这两对是有显著负相关关系的，其余各对是没有相关关系的。关于这个例题的详细讨论请看9.3节。