我的书签
添加书签
移除书签5.4 方差检验
5.4.1 单正态总体方差检验
在实际问题中，常常要检验一批数据的方差是否比设定的值大，或是否已经变小。例如，希望检验本次购进的原材料的方差是否比供应商宣称的要大？改进工作后的方差是否比改进工作前的方差（作为固定值是已知的）有所降低？这些都导致我们要进行单正态总体的方差检验。
1．临界值法
我们计算出检验统计量的观测值，看它是否落在拒绝域内，从而做出判断。
（1）关于总体方差σ2常用的三对假设：
（2）检验统计量选择χ2统计量，在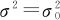
时：
服从自由度为n－1的卡方分布。
（3）对应这三对假设，它们各自的拒绝域分别为：
1）H1：
时，拒绝域是：
2）H1：
时，拒绝域是：
3）H1：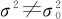
时，拒绝域是：
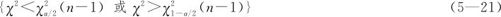
2．p值比较法
通过MINITAB软件指令“统计＞基本统计量＞单总体方差（Stat＞Basic Statistics＞1-Variance）”来实现。
例5—11
某种金属丝折断力服从N（μ，64），μ未知，现随机抽取了30根做折断力试验，测得其数据见表5—8（数据文件：BS_单总体方差检验.MTW）。试问在α＝0.05水平上能否认为这批金属丝的折断力标准差仍然是8？
表5—8
解 应用MINITAB，打开“BS_单总体方差检验.MTW”数据文件，直接对单正态总体标准差进行假设检验。
建立假设：
H0：σ＝8
H1：σ≠8
（1）从“统计＞基本统计量＞单方差（State＞Basic Statistics＞1Variance）”入口；
（2）如图5—16所示输入数据，输入变量名后，选定“进行假设检验”，再选中“假设标准差”（如果要检验的是方差，就可以选择“假设方差”）。
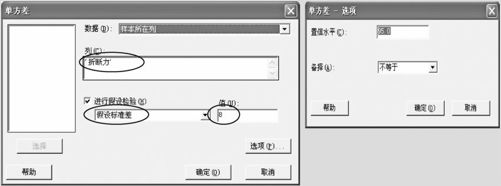
图5—16 单方差检验操作图1
（3）点击“确定”后，得到如下输出结果：
单方差检验和置信区间：折断力
方法
卡方方法仅适用于正态分布。
Bonett方法适用于任何连续分布。
统计量
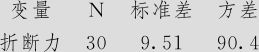
95％置信区间
检验
（4）输出结果说明。由于已知金属丝折断力服从正态分布，看到输出结果p值＝0.139＞0.05，因此我们的结论是：不能拒绝原假设，即认为这批金属丝的折断力标准差还是8。此例说明，当样本量较小时，样本的标准差（或方差）的波动可以是很大的。原来总体标准差是8，现在样本的标准差是9.51，在稍微有些变化时不能认为总体标准差已经发生变化。在实际工作中，如果是为了讨论有关平均值问题，样本量应该超过15；如果是为了讨论有关方差问题，样本量应该超过30；本例勉强达到要求，否则是得不到有意义的结论的。
在MINITAB的早期版本（R14及以前）中，对于单总体的方差检验没有专门的窗口，只能用原始数据计算出标准差的置信区间（例如用“统计＞基本统计量＞图形化汇总（STAT＞Basic Stat＞Graphical Summary）”），然后将此置信区间与要检验的值比较。但用置信区间进行检验仍有局限性，这是因为，使用置信区间一般只能进行双侧检验，对于单侧检验则要麻烦得多（要将α加倍，再看其单侧置信限）。
对于此例，我们可以使用“统计＞基本统计量＞图形化汇总（STAT＞Basic Stat＞Graphical Summary）”入口，求出标准差的95％双侧置信区间为（7.57，12.78），而总体标准差8落入此置信区间，因此不能拒绝原假设，认为这批金属丝的折断力标准差还是8。
例5—12
车工生产精密轴杆，其长度的规格限为15±0.3。原来的标准差已达到0.1，过程能力达到4个西格玛水平。现经六西格玛团队完成黑带项目，过程能力达到5个西格玛水平。现随机抽取了30根轴杆测量其长度，数据见表5—9（数据文件：BS_轴杆长度.MTW）。
表5—9
试问在α＝0.05水平上能否认为这批轴杆长度的标准差比原来的0.1确实有所降低？
解 应用MINITAB，打开“BS_轴杆长度.MTW”数据文件，直接对单正态总体方差进行假设检验。
建立假设：
H0：σ＝0.1
H1：σ＜0.1
（1）从“统计＞基本统计量＞单方差（Stat＞Basic Statistics＞1 Variance）”进入相关界面。
（2）如图5—17所示输入数据，注意在图5—17左半图中选择“假设标准差”。
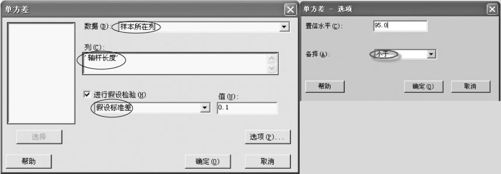
图5—17 单方差检验操作图2
（3）点击“确定”后，得到如下输出结果：
单方差检验和置信区间：轴杆长度
方法
卡方方法仅适用于正态分布。
Bonett方法适用于任何连续分布。
统计量
95％单侧置信区间
检验
结果是p值＝0.030（分布为正态，所以只看上面这行），拒绝原假设，即可以断言轴杆长度的标准差比0.1确实有所降低。
这里要注意的是，如果把此问题当作双侧检验，则结论会稍有差异。从“统计＞基本统计量＞图形化汇总（Stat＞Basic Statistics＞Graphical Summary）”入口，求出标准差的95％双侧置信区间为（0.061，0.101），而总体标准差0.1落入此置信区间，因此不能拒绝原假设，应认为这批轴杆长度的标准差与原来的0.1无显著变化。
为什么会有这种差别呢？这就是因为假设检验的单侧问题与双侧问题是有很大不同的，在选定备择假设时一定要非常小心。单侧备择假设问题能得到显著结果的，在双侧备择假设问题中不一定能得到显著结果，两者的拒绝域是有差别的。当然在通常情况下，单侧备择假设问题能得到显著结果的，在双侧备择假设问题中一般也能得到显著结果，但举上述这个例子的目的是给大家敲个警钟。另外，本例题的计算只能在MINI-TABR15版本增加了新功能后才能进行，在以前的版本中没有此功能。这里要再次提醒大家关于样本量的问题：对于均值方面的检验，样本量至少应该是15以上，对于方差（或标准差）方面的检验，样本量至少应该是30以上。正如在计算过程能力时要求样本量达到50，达到30属于“勉强可以”。样本量太小时是不可能进行有关方差（或标准差）方面检验的。
许多统计工具如双样本t检验（2-Samplet）、方差分析（ANOVA）等，都要假定总体方差相等，因此还要讨论双总体等方差检验或多总体等方差检验等问题。
5.4.2 双总体等方差检验
在实际问题中，常常要检验两批数据的方差是否可以认为是相等的，例如，希望检验两批购进的原材料的方差是否相等？改进工作后的方差是否比改进工作前的方差有所降低？另一方面，双样本t检验（2-Samplet）要在假定两总体方差相等的条件下才能进行，这些都导致我们要进行双正态总体的方差检验。
1．临界值法
我们计算出检验统计量的观测值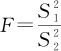
，看它是否落在拒绝域内，从而做出判断。
（1）常用的三对假设：
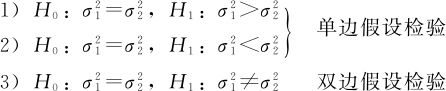
（2）检验统计量选择F统计量，在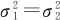
时：
（3）对应这三对假设，它们各自的拒绝域分别为：
1）H1：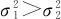
时，拒绝域是：
2）H1：
时，拒绝域是：
3）H1：
时，拒绝域是：
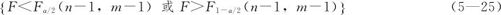
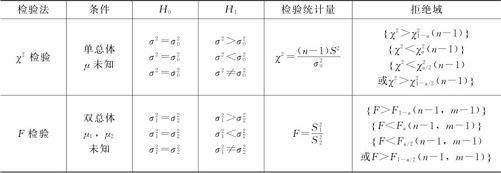
单／双正态总体方差的显著性水平为α的检验中检验统计量和拒绝域等见表5—10。
表5—10 单／双正态总体方差的显著性水平为α的检验
2．p值比较法
通过MINITAB软件指令“统计＞基本统计量＞双方差（Stat＞Basic Statistics＞2-Variances）”来实现。
例5—13（续例5—8）
一家冶金公司需要减少其排放到废水中的生物氧需求量（BOD）含量。考虑用纯氧取代空气吹入活化泥以改善BOD含量。在两种处理的废水中，空气法抽了10个样品，氧气法抽了9个样品，数据见表5—11（数据文件：BS_生物氧需求量.MTW）。
表5—11
已知BOD含量服从正态分布，问在显著性水平α＝0.05下，该公司采用这两种不同方法对BOD含量影响的方差是否相等？
解 （1）建立假设：
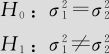
（2）在正态条件下，可以用F检验。
（3）据显著性水平α＝0.05及备择假设可知拒绝域为：
（4）样本观察值，求得
由于样本观察值未落在拒绝域中，因此不能拒绝原假设，可以认为该公司采用这两种不同方法对BOD含量影响的方差是相等的。
由于F检验的拒绝域是双侧，使用者必须同时考虑F值的拒绝范围：F太大要拒绝，F太小也要拒绝。为了使判断中的思考简化，不少中外六西格玛黑带培训教材中建议，在F统计量的计算中规定要使分子大于分母，这样一来，拒绝域可以只考虑右侧，也就是说只考虑F值太大则拒绝。这种处理方法可以简化我们的思考，但是若把F定义为分子大于分母则又是错误的（这时F肯定大于1，根本不再是F分布了），拒绝域取为右侧5％也是错误的（应该仍保留2.5％）。本书在此特别予以提醒，请大家在使用时注意。
使用MINITAB软件求解本题步骤：
（1）建立假设：
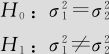
（2）从“统计＞基本统计量＞双方差（Stat＞Basic Statistics＞2-Variances）”进入相关界面。
（3）输入数据后，在“图形”中勾选“区间图”和“箱线图”。点击“确定”后，得到下列输出结果及图5—18。
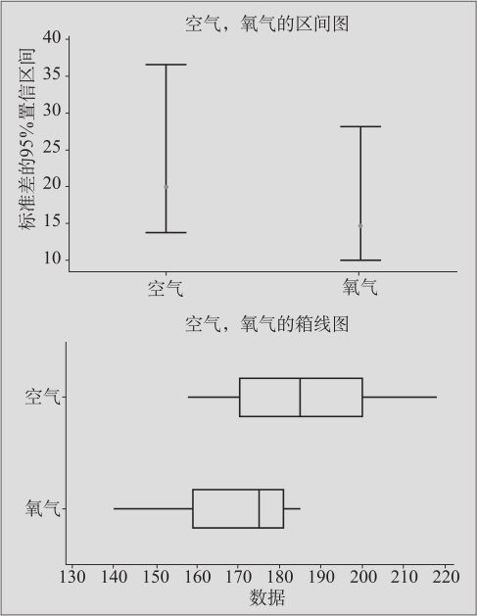
图5—18 两总体方差相等性检验1
双方差检验和置信区间：空气，氧气
方法
统计量
标准差比＝1.358
方差比＝1.845
95％置信区间
检验
（4）输出结果说明。由于BOD含量服从正态分布，输出的F检验的p值＝0.401＞0.05，因此我们的结论是：不能拒绝原假设，该公司采用这两种不同方法对BOD含量影响的方差是相等的。
值得注意的是，对于等方差检验输出有两种检验结果：
●F检验，适于正态数据。
●Levene检验：是以样本中位数而非样本均值为基准，在小样本时更稳健，适于非正态连续数据。
如何比较F检验和Levene检验这两种方法呢？从表面上看，Levene检验适用于任何类型连续性分布，当然也适用于正态分布，应用范围要比F检验广泛得多。那么是否可以说Levene检验要比F检验“好”呢？不能这样说。大家都知道有种药叫“板蓝根”，它可以治感冒、淋巴腺炎、扁桃腺炎、腮腺炎、肝炎，预防“非典”，最近发现又增加一项“抗高原反应症”功能。能说它是“天下第一药”吗？恐怕不能。得了肝炎，在治疗时很少有人再去用板蓝根，因为市面上有很多专门治疗肝炎的药，在治疗肝炎时，用板蓝根绝对不如那些专门治疗肝炎的药。对于检验两总体方差相等性这个问题，如果数据为正态分布，F检验绝对是最灵敏（也就是犯第二类错误最小）的方法，只有当数据为非正态时，F检验不能使用了，才会使用Levene检验方法。
例5—14（续例4—8）
假定A，B两名工人生产相同规格的轴棒，关键尺寸是轴棒的直径。由于A使用的是老式车床，B使用的是新式车床，二者精度可能有差异。现他们各测定了13根轴棒直径的结果（数据见例4—8，数据文件：BS_轴棒直径.MTW）。试分析A，B两名工人生产的轴棒直径的方差相等吗？
解 建立假设：
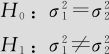
与例5—13所叙述的操作完全相同，由于二者皆为正态分布，因此可以得到下列结果及图5—19。
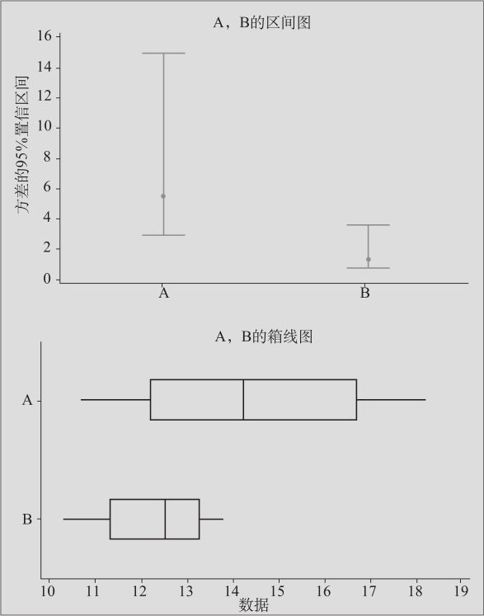
图5—19 两总体方差相等性检验2
双方差检验和置信区间：A，B
方法
统计量
标准差比＝2.038
方差比＝4.152
95％置信区间
检验
从计算结果中可以看出，两样本方差之比高达4.15，两样本方差相差这么多倍，p＝0.02＜0.05，结论应该是拒绝原假设，即可断言两总体方差并不相等。
