6.2　双总体比率检验

我们常需要对两个总体的比率进行比较，比如希望了解在两种工艺方法条件下产品不合格品率是否有显著差别，采用某种服务方法是否比另一种服务方法让顾客满意率有显著提高等。这类问题我们通常可以通过双总体比率检验方法予以处理。

设样本X₁，X₂，…，X_n来自二点分布总体X，X～b（1，p₁），样本Y₁，Y₂，…，Y_m来自二点分布总体Y，Y～b（1，p₂），两样本独立。我们希望检验的假设是这种类型：H₀：p₁＝p₂，H₁：p₁≠p₂，当然备择假设可以换成“＞”或“＜”。此问题可以改用“比率差”的说法：H₀：p₁－p₂＝0，H₁：p₁－p₂≠0，也可以更一般化地提出检验问题：H₀：p₁－p₂＝d，H₁：p₁－p₂≠d，当然备择假设也可以换成“＞”或“＜”的形式。这里d就是要检验的两总体的比率差。当然实际工作中，d＝0是最常见的情况。

引入以下记号：

在对参数p₁－p₂进行检验时，对于d取值是否为0，其检验统计量的形式稍有差别。以下分两种情况分别给出：

（1）p₁－p₂＝d（其中d≠0）时：

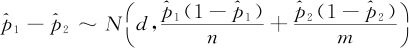
对其作标准化变换，得到统计量：

由此可以得到相应的拒绝域。其结果列在表6—2中。

表6—2　两个比率差为d的显著性水平为α的检验

（2）p₁－p₂＝0时，p₁与p₂可以使用公共的估计量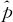（表达式见式（6—4））。

由于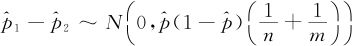，因此统计量

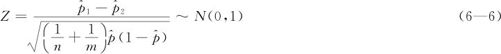
由此可以得到相应的拒绝域。其结果列在表6—3中。

表6—3　两个比率差为0的显著性水平为α的检验

例6—2

分别从A，B两种工艺条件下随机抽取1500片及1800片芯片，其中A种工艺条件下有340片为一等品，B种工艺条件下有350片为一等品。在α＝0.05下，检验A种工艺条件是否比B种工艺条件有较高的一等品率。

解　设p₁，p₂分别表示A，B两种工艺条件下的一等品率，此时要检验的假设为：

H₀：p₁＝p₂

H₁：p₁＞p₂

由所给出的备择假设，利用大样本的正态近似性，得出在α＝0.05水平上的拒绝域为{Z＞1.645}。

由样本数据知n＝1500，m＝1800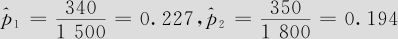，，可知：

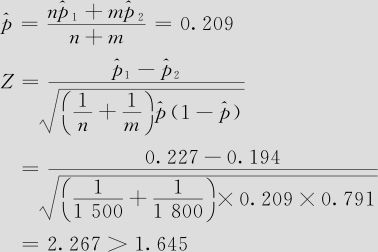
落在拒绝域中，拒绝原假设，即在α＝0.05水平上，A种工艺条件比B种工艺条件有较高的一等品率。

用MINITAB软件计算，从“基本统计量＞双比率（Stat＞Basic Statistics＞2 Proportion）”进入相关界面，输入相关数据后，得到下列结果：

双比率检验和置信区间

差值估计：0.0322222

差值的95％置信下限：0.00873597

差值＝0（与＞0）的检验：Z＝2.26　P值＝0.012

Fisher精确检验：P值＝0.013

这里p值＝0.012＜0.05，得到同样的结论：拒绝原假设，即在α＝0.05水平上，A种工艺条件比B种工艺条件有更高的一等品率。

例6—3

同种产品有甲、乙两种品牌。随机抽取800位及600位各自购买了甲、乙两种品牌的顾客，其中甲品牌有340位顾客对其产品质量表示满意，乙品牌有180位顾客对其产品质量表示满意。在α＝0.05下，检验甲品牌的顾客满意率是否比乙品牌的顾客满意率高5％以上。

解　设p₁，p₂分别表示甲、乙两种品牌的顾客满意率，此时要检验的假设为：

H₀：p₁－p₂＝0.05

H₁：p₁－p₂＞0.05

由所给出的备择假设，利用大样本的正态近似性，得出在α＝0.05水平上的拒绝域为{Z＞1.645}。

由样本数据知n＝800，m＝600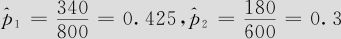，，可知：

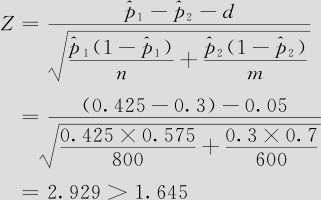
落在拒绝域中，拒绝原假设，即在α＝0.05水平上，甲品牌的顾客满意率比乙品牌的顾客满意率高5％以上。

用MINITAB软件计算，通过“基本统计量＞双比率（Stat＞Basic Statistics＞2 Proportion）”进入相关界面，如图6—3所示。

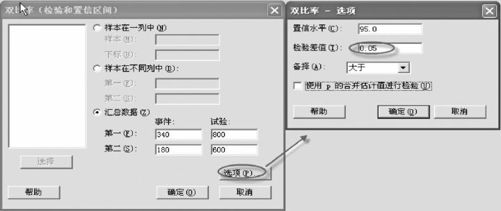
图6—3　双比率检验操作图

输入相关数据后，得到下列结果：

双比率检验和置信区间

差值估计：0.125

差值的95％置信下限：0.0828883

差值＝0.05（与＞0.05）的检验：Z＝2.93　P值＝0.002

这里p值＝0.002＜0.05，拒绝原假设，得到同样的结论：拒绝原假设，即在α＝0.05水平上，可以断言甲品牌的顾客满意率比乙品牌的顾客满意率高5％以上。