7.2　秩和检验法及Mann-Whitney检验法

除了使用“符号”这个工具，非参数检验方法中另一个强有力的工具是秩（rank），意为名次。我们先把秩的概念严格化。例如有11个数据，如何给它们赋予名次呢？一般来说这很容易，从小到大排好队后，立即可以得到名次。但遇见数据相等（称为“结”（tie））时则要恰当处理才行。在运动会上，如果第二名、第三名成绩一样，会称他们“并列亚军”，但这样处理在讨论检验性能时很不方便，所有数据的所有秩的和会因为有“并列”而发生变化。我们将之改进而采用“平均”的办法，将原来两个数据的2与3名，平均得到每个数据都是第2.5名。依此类推，如果3个或多个数据相同，则它们的共同秩是原来应有的秩的平均。请看表7—3中排好了的数据及它们相应的秩：

表7—3

如“14”有两个，原应位于3、4名，故它们都是3.5名；“19”有3个，原应位于第7，8，9名，故它们现在都是第8名。MINITAB可以对数据列自动计算出相应的秩，具体操作见例7—6。

对于给定的两组数据，如何检验它们的均值（或中位数）间是否有显著差异呢？先来解释一下我们的思考方法。

由于两组观测值个数不一定相等，我们称样本量较小的一组为“第一组”（样本量相同时，可以任意指定一组）。要检验的假设是两组中位数是否相等：

或者全部移至左侧，将检验写成：

如果将两组全部数据混合在一起，排出各数据之秩，再将各组内所有的秩相加，求出“秩和”（sum of rank）。我们先分析一下，式（7—6）中“H₀成立”与“H₀不成立”对秩和会有什么影响。

在图7—4中，我们用“○”代表第一组数据（样本量稍小者），而用“”代表第二组数据。如果第一组中位数明显比第二组要小，则第一组的秩和肯定应该比第二组的秩和要小很多（见图7—4（a））；如果第一组中位数明显比第二组要大，则第一组的秩和肯定应该比第二组的秩和要大很多（见图7—4（b））；如果两组中位数相差不大，则两组的秩和应该差不多（见图7—4（c））。因此，可以用秩和的差别是否足够大来判别两组中位数差异是否显著，即当第一组的秩和偏大或偏小都应拒绝H₀。差异到多大才算“差异显著”？可以根据两样本的数量查附表9得到临界值，具体计算过程参见例7—6。归纳起来说是：将两组数据合并排序并给每个观测值一个秩值，计算出样本量较小者组内所有秩的和T，查本书附表9中对应α＝0.025的左半栏（这是针对秩和值太大或太小双侧都拒绝的问题给出的，右半栏是针对单侧拒绝域给出的），得到临界值的下界T₁，上界T₂。若T≤T₁或T≥T₂，则拒绝原假设。当样本量之一超过10，则可以使用近似正态检验法。在历史上，首先是由威尔科克斯（F. Wilcoxon）在1945年提出了这种两样本之样本量相等条件下的秩和检验，曼（Mann）和惠特尼（Whitney）于1947年将此方法推广到两样本量不等的情况，所以常称双样本中位数检验方法为Wilcoxon-Mann-Whitney检验（WMW检验），在MINITAB的菜单上标注的是Mann-Whitney检验。

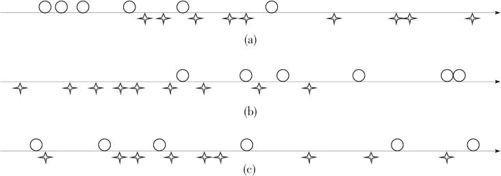
图7—4　双样本秩和检验示意图

例7—6

抽查两种工艺条件下生产的电容器，在固定的高电压脉冲冲击下，其寿命是产品质量的关键指标。A组抽取10片，B组抽取8片，记录其寿命的观测值如表7—4所示（耐冲击次数，单位：千次）（数据文件：NP_两组电容寿命.MTW）。试分析两种工艺条件下的电容器寿命有显著差异吗？（取α＝0.05）

表7—4

解　我们要检验的问题是两组中位数之差是否为0：

H₀：η₁－η₂＝0H₁：η₁－η₂≠0

注意到这两组寿命数据都不是正态分布的，不能使用双样本t检验来检验平均值之差是否为0。

先用MINITAB将全部18个数据堆叠为一列，并按由小到大排序，从“数据＞堆叠＞列（Data＞Stack＞Column）”入口，可得下列界面（见图7—5）。

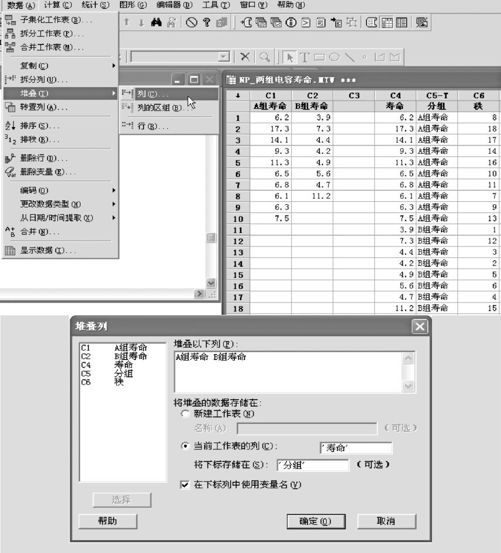
图7—5　双样本堆叠数据操作图

对于堆叠好的数据（见图7—5中上图C4及C5两列）可以使用MINITAB排秩功能将其秩的数值求出。从“数据＞排秩（DATA＞Rank）”入口，得到如图7—6所示界面，填写好有关信息（见图7—6），则可以得到图7—5中上图最右一列的数据。

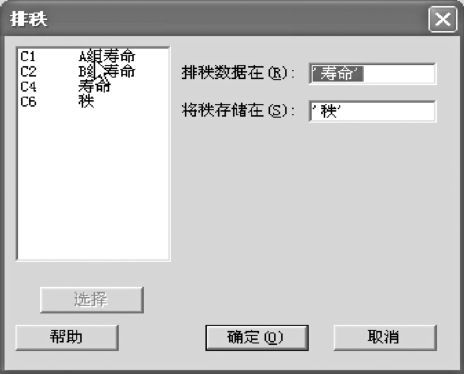
图7—6　数据排秩操作图

下面我们先用手算非参数检验法来检验中位数之差是否为0，以了解全部计算细节，然后再学会用计算机计算。

B组样本量较小，从排秩结果中可以求得B组的秩和为：

T＝1＋12＋3＋2＋5＋6＋4＋15＝48

查附表9，对应于n₁＝8，n₂＝10，在左栏查得接受域为（54，98），T值比下界54还小，落在接受域之外了，因此应拒绝原假设，即认为两种工艺生产的电容器寿命间有显著差异。

以上是对于小样本，自己动手计算的过程与步骤。实际工作时，不用这样麻烦，特别如果有一组数据超过10，则因附表9未涵盖，还要用近似正态方法获得。MINITAB中的Mann-Whitney检验可以适用于任意大小的样本量。下面介绍用MINITAB的操作。依次选择“统计＞非参数＞Mann-Whitney（Stat＞Nonparametric＞Mann-Whitney）”，填写两组变量名即可得到结果。

Mann-Whitney检验和置信区间：A组寿命，B组寿命

ETA1－ETA2的点估计为2.300

ETA1－ETA2的95.4置信区间为（0.900，6.601）

W＝123.0

在0.0145上，ETA1＝ETA2与ETA1≠ETA2的检验结果显著

这里给出了检验结果的p值＝0.0145，因此应该拒绝原假设，即可以断言两总体中位数间有显著差异。在两组合并样本中，样本量一共为18，两组样本全部秩之和是固定常数，即为从1到18的全部整数的和：1＋2＋…＋18＝171，前面手算获得B组秩和为48，所以A组秩和为剩余部分：W＝171－48＝123。ETA1－ETA2的点估计并不是两组中位数之差，而是所有两组的配对观测值之差的中位数；置信区间的计算公式是这样的：先将所有可能的配对观测值按A组减B组求出差值，将其由小到大排序，选出大于给定置信水平的置信区间中长度最短者，当然也有近似估计公式可用（可以参看参考文献［9］：吴喜之所编的《非参数统计》），这里就不详细介绍了。但应注意，因为数据属于离散数据，因而不一定能恰好得到指定置信水平的置信区间，这里给出的是最近似指定置信水平（这里是95.4％）的结果，由于置信区间不包含0，因此应拒绝原假设。结论与秩和法的查表结果一致。

双样本的Wilcoxon-Mann-Whitney（WMW）检验，在样本确实服从正态分布时虽然不如双样本t检验，但其渐近效率（这里不给出严格定义）高达0.955，两种检验效果差不多；而对于非正态（例如非对称分布），WMW检验反而比t检验要好。因此在进行双样本均值（或中位数）检验时，究竟是否要选用非参数方法，强烈地依赖于数据的分布状况。

例7—7

某市举行中学生长跑比赛。A，B两校都参加了比赛，各自获得的名次如表7—5所示（数据文件：NP_长跑比赛.MTW）。

表7—5

试分析两个学校长跑成绩有显著差别吗？（取α＝0.05）

解　由于数据是有序数据，是离散型数据，不能用连续变量方法来分析。对于这种数据我们仍然可以使用Mann-Whitney检验法。其操作步骤与例7—6完全一样，这里就不列出了。其结果为：

Mann-Whitney检验和置信区间：A校，B校

ETA1－ETA2的点估计为-18.50

ETA1－ETA2的95.6置信区间为（-29.01，-1.01）

W＝106.0

在0.0378上，ETA1＝ETA2与ETA1≠ETA2的检验结果显著

由于p值＝0.0378，因此结论是“两校长跑成绩有显著差别”。

在数据中出现结时，计算机将自动给出对错的修正结果，这时应以修正结果为准。