8.2　关于分布的探索性分析

我们先来讨论有关数据分布状况的工具。这里包括茎叶图、箱线图、字母图和根状图。

8.2.1　茎叶图

对于一批数据，我们首先希望能直观地看出它的各方面特征，例如数据批的接近对称程度，有多大的散布，是否有野值，是否有数据的集中及间隙等。茎叶图（stem-and-leaf display）就是用简单的图示方法把数据特征展现出来。

例8—1

对于参加统计课学习的某班92名学生测量了一些有关脉搏的指标。脉搏1是静息脉搏，脉搏2是运动脉搏。数据见表8—1（数据文件：EDA_脉搏.MTW）。试讨论静息脉搏的分布状况。

表8—1　学生脉搏数据

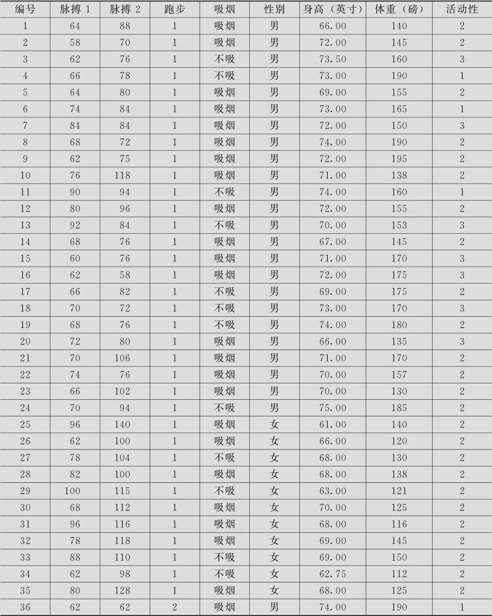
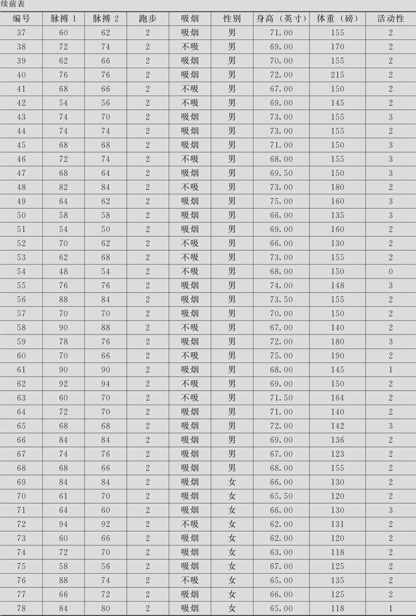
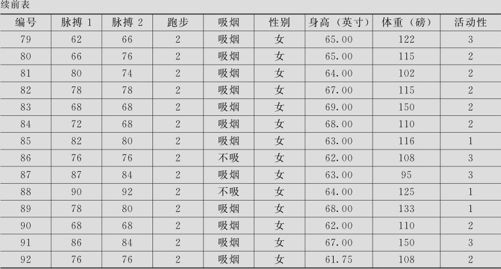
传统统计方法可以用直方图描述数据的分布状况。对于绘制直方图的方法，我们已在第3章给出。下面先给出直方图结果（见图8—1）。

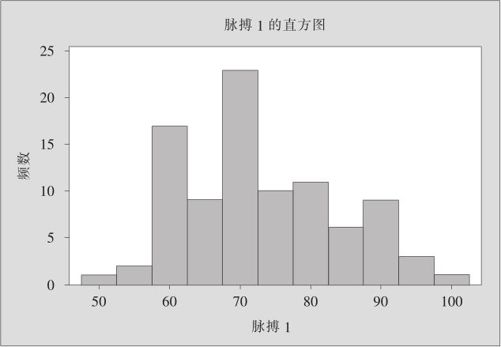
图8—1　学生脉搏直方图

根据上述图形可以看出数据分布的大致状况，但直方图也省略了很多细节，例如，脉搏为60附近（其实是介于57.5～62.5）的数据究竟有哪些？从直方图中是显示不出来的。即使换成“点图”，虽然每个点都能表示出来，但也经过了整理合并，损失了些细节。EDA使用茎叶图可以弥补这些缺陷。

从“统计＞EDA＞茎叶图（Stat＞EDA＞Stem and Leaf）”入口，在“图形变量（Graph Variables）”中填写入“脉搏1”（见图8—2），即可绘制出茎叶图。

图8—2　绘制茎叶图操作图

操作后可以得到输出结果如下（见图8—3）：

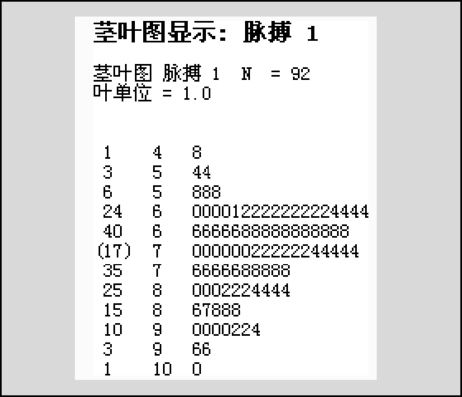
图8—3　学生脉搏茎叶图

绘制茎叶图的原理是：将每个数据分为“茎”和“叶”两部分，例如，学生脉搏为68，则可将60作为“茎”，将8作为“叶”。数据较多时（如本例），可以将茎分得稍细些，例如“60”，“65”都作为“茎”，60～64，65～69分列为两个“茎”。在图8—3中，将所有茎的值从小到大排列好，列于图中左侧第二列；将“叶”的数值列在其后。例如，茎为6的分成两部分，在60～64部分中，60有4个，61有1个，62有9个，63有0个，64有4个；在65～69部分中，66有5个，68有11个。从茎叶图中同样可以看见分布状况的总轮廓，包含数据较多的区间将导致“叶”较长，比如从本例学生脉搏茎叶图中可以明显看出，在60～74这段范围中，包含了较多的数据。它对于分布状况的描述与直方图功能相仿，但茎叶图增加了很多信息，主要是它无合并地提供了每个数据的状况。

作为茎叶图的另一特点，在图8—3中的茎叶图之最左列，给出了数据的累积深度。例如，48是深度为1的最小值；数值为54的数据有2个，截止到54时，深度已达到3；数值为58的数据有3个，截止到59时，深度已达到6，等等。同样从高端算起，100是深度为1的最大值；数值为96的数据有2个，截止到95，深度已达到3；数值为94的数据有1个，数值为92的数据有2个，数值为90的数据有4个，截止到90时，深度已达到10，等等。在最中间的一格内（用圆括号括起来的）指明中位数所在的区间，以及在本区间所包含的数据个数。本例中，可以得知中位数位于70～74组内，且本组共包含17个数据。茎叶图还有一个重要用途，那就是可以求出任意指定深度的观测值，例如本例中，可以求出深度为46的是哪个数值，其计算方法是：（1）从下端算起，由于下侧第5组累积已有40个观测值，因而深度为46的是此组的下组（茎为70）的第6个观测值70（即是升秩为46者）；（2）从上端算起，由于上侧第6组累积已有35个观测值，因而深度为46的是此组的上组（也是茎为70的那组）的第11个观测值72（即是降秩为46者）；中位数应是二者的平均值，因而中位数是71。

8.2.2　箱线图

对于一批数据，除了希望能直观地看出全部数据的各方面特征，还希望同时对于多个小组数据的各方面特征都能有比较直观的展现。箱线图（box plot）就是用简单的图示方法把多个数据组的特征同时展现出来。

我们已在8.1.3节中介绍了在EDA中常用的统计术语，其中描述数据分布状况的有下列五个最重要的数：中位数M，下四分数F_L，上四分数F_U，F_L－1.5d_F及F_U＋1.5d_F，通常称为“五数概括”。用下四分数F_L及上四分数F_U分别作箱子的两端，用M作中心线，用F_L－1.5d_F及F_U＋1.5d_F分别作为尾线的端点X^L及X^U，这就是箱线图。如果在两尾端之外还有观测值，则可以认为是“可疑异常值”。总之，箱线图可以直观地显示出一批数据的位置、散布、偏度、尾长和离群值状况。它与传统的箱线图一样都有很强的耐抗性，经得起少数异常数据的影响，长方形箱外即使有多个数据远离长方形箱也不会引起长方形箱位置及大小的变化。

从“统计＞EDA＞箱线图（Stat＞EDA＞Box Plot）”入口，选中左上角“一个Y、简单（One Y，Simple）”窗，在“图形变量（Graph Variables）”中填写入“脉搏1”（图省略），即可绘制出箱线图（见图8—4）。

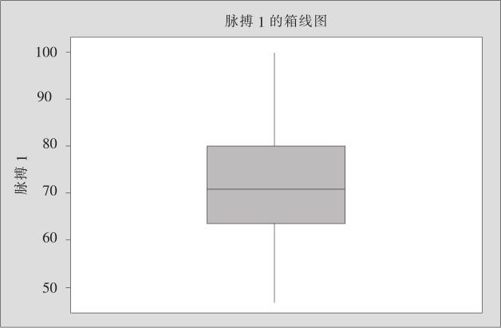
图8—4　学生脉搏箱线图

粗略看来，EDA的箱线图与原来传统的箱线图似乎完全相同，但实际上仍有微小差异，尤其当样本量较小时差异更大些。因为EDA中“五数概括”是：中位数M，下四分数F_L，上四分数F_U，F_L－1.5d_F及F_U＋1.5d_F；而传统的箱线图是由中位数M，下四分位数LQ，上四分位数UQ，LQ－1.5IQR及UQ＋1.5IQR这5个数构成，二者是有微小差别的。

与传统的箱线图相似，EDA的箱线图同样也可以显示多个组之间的差异。如本例，希望给出男女生脉搏的比较，则可以绘制出分组的箱线图。从“统计＞EDA＞箱线图（Stat＞EDA＞Box Plot）”入口，选中右上角“一个Y、含组（One Y，With Group）”窗，在“图形变量（Graph Variables）”中填写入“脉搏1”并加选“用于分组的类别变量”为“性别”（图略），即可绘制出脉搏1数值的分性别的箱线图（见图8—5）。

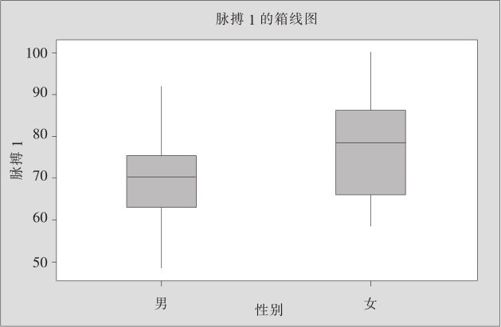
图8—5　学生分性别的脉搏箱线图

从图8—5中容易看出，女生的脉搏明显高于男生的脉搏。

8.2.3　字母图

对于一批数据，除了希望能直观地看出数据各方面的特征外，还希望能归纳出一些摘要性的数值特征结果。上面提到的“五数概括”就是其中一个很好的代表，这里给出了中位数M，下四分数F_L，上四分数F_U，F_L－1.5d_F及F_U＋1.5d_F。如果数据量更大，需要对双侧尾部更大范围内状况加以描述，就需要增加一些量，例如在五数概括的基础上，再增加两个上下八分数，则可以组成七数概括；在七数概括的基础上，再增加两个上下十六分数，则可以组成九数概括，等等。为了让这些分数有系统化的名称以能更方便地表示这些值，EDA规定：从字母F代表四分数开始按英文字母表的倒序，一个一个字母倒退，字母E代表八分数；字母D代表十六分数；字母C代表卅二数；字母B代表六十四分数；字母A代表一百二十八分数；如果还要再向下分，则用字母Z代表二百五十六分数；字母Y代表五百一十二分数；字母X代表一千零二十四分数；……

MINITAB则以H（hinges，折叶点）代表四分数，与一般命名法不全相同，但高阶分数E，D，C，B，A则与一般命名法恢复一致。

我们已知四分数与中位数深度关系为（见式（8—3））：

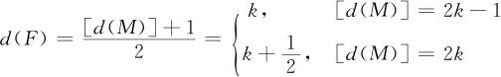
更一般地，对于后深度与前深度有关系：

这里中括号代表取整数之函数。式（8—7）的含义是，如“前深度”是指中位数深度，则“后深度”是指四分数深度；“前深度”是指四分数深度，则“后深度”是指八分数深度；依此类推。

将各字母相应的取值及上下两字母间的差值全部列出来，对于数据的双尾状况的显示是非常有用的，特别是它可以用来分析数据批的展布程度的耐抗量度，或用来搜索离群值。MINITAB软件将自动完成上述任务，给出各字母值。

仍以学生脉搏数据为例，从“统计＞EDA＞字母图（Stat＞EDA＞Letter Values）”入口，在“变量（Variables）”中填写入“脉搏1”（图略），即可得出相应的字母值（见图8—6）。

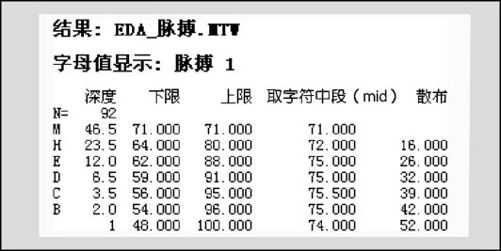
图8—6　学生脉搏的字母图

从图8—6中可以看出，中位数深度为d（M）＝46.5，中位数为71；两个四分数（或折叶点）深度d（F）＝23.5，下、上四分数分别为64及80，中点是下、上四分数的平均值，此数也称为四分数的“中概括（MidF）”，MidF＝72，散布（即四分展布）为16；两个八分数深度d（E）＝12，下、上八分数分别为62及88，中点MidE＝75，散布为26；两个十六分数深度d（D）＝6.5，下、上十六分数分别为59及91，中点MidD为75，散布为32＝6；…；两个六十四分数深度d（B）＝2，下、上六十四分数分别为54及96，中点MidB＝75，散布为42；两个极端值深度皆为1，极小值和极大值分别为48及100，中点也称为“极差中值”（center of range），极差中值为74，散布（即极差）为52。从本例数据所得到的若干个中点概括值几乎不变，说明数据状况基本上是对称的。

从理论上分析，由于高斯分布的四分数为μ±0.6745σ，四分散布为1.349σ，因而也常用四分散布除以1.349得到σ的估计量，此量常称为“四分伪标准差”（F-pseudosig-ma），它具有很好的耐抗性。通常情况下，此估计量应该与样本标准差S很接近。如果这两个估计量相差悬殊，则通常宁可用四分伪标准差也不用样本标准差S，因为样本标准差对极端值太敏感，四分伪标准差则要好得多。这是我们从EDA中得到的重要结论之一。

8.2.4　根状图

对于一批数据，悬浮式根状图是拟合了正态分布后偏离量的直方图，它显示与所拟合正态分布的偏差。其计算的原理是：按小组计算出实际数据的各百分位数，同时计算出相应的正态分布的百分位数，再计算出二者的差别“原始残差”（raw residual，RR），最后算出“双根号残差”（double root residuals，DRR），并将双根号残差展现成悬浮式根状图。我们可以从根状图中看出是否存在与正态分布偏离特别大的分布非正态的异常状况。对于第i组，记实际观测频数为n_i，正态分布相应频数为f_i，定义原始残差为：

定义双根号残差DRR_i为：

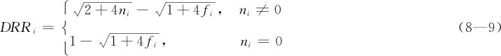
可以看出，DRR的核心部分是：

在样本量足够大的情况下，DRR_i应该是标准正态分布，也就是说其值绝大多数应落在（-2，2）之内，偶尔可以落在其外，但除非极特殊情况一般也不能超出（-3，3）。从DRRi的值是否有极端异常值可以判断数据与正态分布是否有较大差异。

从“统计＞EDA＞根状图（Stat＞EDA＞Rootogram）”入口，得到如图8—7所示界面，在“变量（Variables）”中填写入“脉搏1”，选定多列作为存储结果用（见图8—7）。

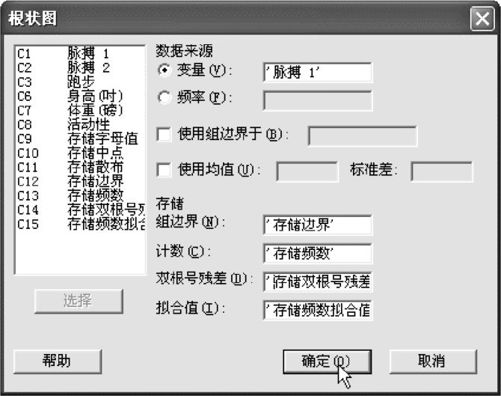
图8—7　学生脉搏根状图的操作

在此界面中显示出，数据允许有多种记录格式，例如可以是原始数据记录格式，也可以是分组并记录其频数的格式等。存储计算结果可供以后备查，以便显示偏离最大的组的细节。

运行后得到的悬浮式根状图见图8—8。

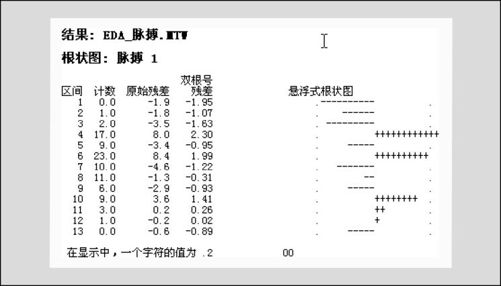
图8—8　学生脉搏的悬浮式根状图

在左半部数值结果显示中，可以看出共分了13组，在“计数”一列中显示了每组内的观测值个数，在“原始残差”一列中显示了根据式（8—8）计算出的组内实际观测值个数与预期的正态观测值个数之差，在“双根号残差”一列中显示了根据式（8—9）计算出的双根号残差。在右半部悬浮式根状图的图形结果显示中，分别用字符“+”或“-”代表双根号残差的符号，每个字符值为0.2，双侧圆点代表正负2的边界线。在本例图中，可以看出13组中只有第4组双根号残差值达到2.3（用12个“+”来显示），已经超出正负2的边界，显示数据与正态分布（高斯分布）有相当的差距。在原始数据文件的最后几列，可以看见存储的细节（见图8—9）。

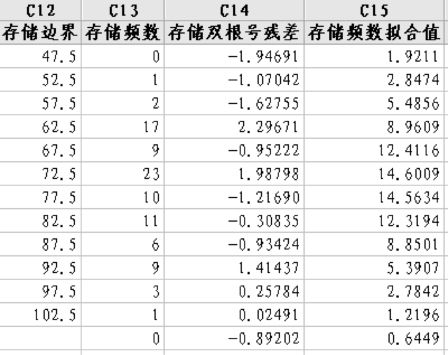
图8—9　学生脉搏的悬浮式根状图数值结果

图8—9中最左列的边界是各组的上界，例如双根号残差的最大值出现在第4组，其值为2.2967，观测值的上界为62.5（即本组包含的是落入57.5～62.5间的数据），实际共有17个观测值，按正态分布计算，此组应有8.96个观测值，代入式（8—9），可得第4组处双根号残差为：

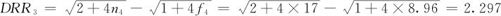
这说明，在偏离正态性的现象中，第4组的观测值个数过多是最重要的原因（第6组的观测值个数也偏多）。如果简单地进行正态性检验，当然同样可以得出“此数据非正态”的结论，但这里给出了更加细致的定量分析结果。

如果双根号残差超过（-3，3）范围，则在悬浮式根状图（见图8—8）的图形显示区内标记出“*”，表示偏离极端严重。