3.3　简单统计图形

单纯的数字和符号往往比较抽象乏味，适当的统计图形会显著增强数据的感染力，帮助人们理解统计分析结果。本节将介绍一些在表现描述性统计信息时最常用的统计图形及其实现方法，主要包括直方图、箱线图、饼图、时间序列图、三维散点图、3D曲面图和矩阵图。

3.3.1　直方图

直方图（histogram）常常用于了解数据的分布情况，使我们比较容易直接看到数据的位置状况、离散程度和分布形状，并且可与要求的分布进行比较。

直方图是用一系列宽度相等、高度不等的长方形表示数据的，其宽度代表组距，高度代表指定组距内的数据数。制作直方图的具体步骤如下：

（1）从n个样本数据中找出最大值a_k＝max和最小值a₀＝min，并计算极差值R＝max-min。

（2）对样本进行分组，决定组数k和组距d。k的取值范围通常在7～15之间，具体值一般随样本量n的增加而增加。d由极差R与组数k来确定，通常定义d＝R/k。

（3）确定各组的区间端点a₀，a₀＋d＝a₁，a₀＋2d＝a₂，…，形成如下区间：

［a₀，a₁），［a₁，a₂），…，［a_k－1，a_k］

（4）计算样本落在每个区间中的频数n_i，根据需要计算频率f_i＝n_i/n和密度D_i＝n_i/nd。

以样本为横坐标，以频数为纵坐标，在每个小区间上竖起一个长方形，它们相连形成一张频数直方图。纵轴的单位也可以用频率或密度表示，得到对应的频率直方图或密度直方图。

例3—3

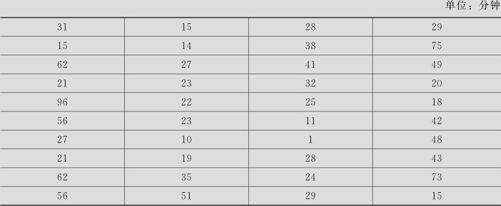
某银行对其所属的某营业网点顾客的等待时间进行抽样调查，其中测量了该网点在2月8日（周五）从上午10点至下午3点间所有顾客（共40人）的等候时间，试绘制直方图（数据列在表3—2中，数据文件：BS_直方图.MTW）。

表3—2　顾客等候时间数据表

解　利用MINITAB的实现方法如下：

（1）选择“图形＞直方图（Graph＞Histogram）”中的“简单（Simple）”。

（2）指定“图形变量（Graph variables）”为“等候时间”，则可得到如图3—4所示的图形输出。

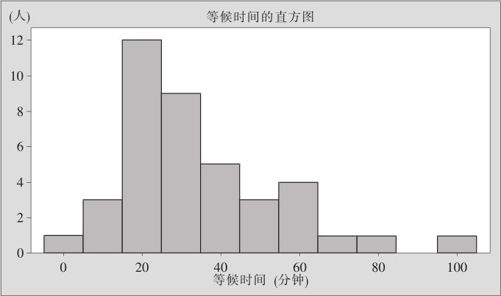
图3—4　顾客等候时间直方图

从图3—4中可以看出，总共40个顾客的等候时间集中在5～65分钟之间，其中又以等候15～25分钟的顾客数量最多，高达12个。数据整体呈明显的正偏（尾部右偏）分布，另外还有一个顾客的等候时间接近100分钟，形成延伸严重的高于均值的尾部。

3.3.2　箱线图

箱线图（boxplot）主要是利用数据中的五个统计量来描述数据的一种图示方法。利用它可以粗略地看出数据是否具有对称性、中心位置和分布范围等信息。此外，对同一性质的多组数据在同一坐标下分别作箱线图，可以直观地进行多组数据比较。

箱线图由箱体、上下须触线和星号三部分组成，图形的形状和位置由最小值、第一四分位数、中位数、第三四分位数和最大值这五个统计量决定。最小值、中位数和最大值的含义大家都很熟悉，第一四分位数Q1和第三四分位数Q3在前面3.2.1节中已作了介绍。

箱线图可以竖直画（见图3—5），也可以横着画（见图3—3）。以下我们用竖直画的箱线图（见图3—5）来说明其具体含义。箱体内位于中间的线代表中位数，箱体的下边界是Q1，箱体的上边界是Q3，箱体的长度对应着四分位间距，即Q3与Q1之间的差值。

图3—5　灯泡使用寿命箱线图

除了箱体之外，还有上下两条须触线。它们分别从箱体的上下边界为始端出发，尾端由上下限的计算公式给出：

上面两个公式的含义是：以下限为例，如果最小值很小，须触线下限将延伸到Q1－1.5IQR处为止；如果最小值较大，须触线的下限将到最小值处为止。上限的含义相同。最后介绍一下星号。如果上下限的计算结果不是观测值中的最大、最小值，箱线图上就会出现一些游离点，这些点有异常值的嫌疑，通常用“*”表示。

例3—4

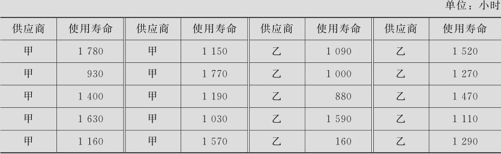
某公司从两家供应商各采购了一批灯泡，分别统计各组样品的使用寿命，试绘制箱线图分析（数据列在表3—3中，数据文件：BS_箱线图.MTW）。

表3—3　灯泡使用寿命数据表

解　利用MINITAB的实现方法如下：

1．选择“图形＞箱线图（Graph＞Boxplot）”中的“一个Y含组（One Y-With Groups）”。

2．指定“图形变量（Graph variables）”为使用寿命，指定“用于分组的类别变量（Categorical variables for grouping）”为“供应商”，则可得到如图3—5所示的图形输出。

从图3—5可以看出，两种灯泡的使用寿命分布的对称性较差，分布均似乎显正偏。供应商乙有一个使用寿命特别短的产品，大小如图中*号所处的位置所示，其原因值得调查。供应商甲的使用寿命似乎略高于供应商乙，同时除去异常值，供应商甲产品的分布范围比供应商乙的似乎略大些，但这些都不能肯定。如果要做出明确的结论，还需经过统计检验（见第5章）。

如果对于图3—5仍觉得不够满意，比如希望增加两供应商灯泡寿命的各自均值位置显示及增加两均值的连线，则可以重复刚才的操作，并打开右下角处的“数据视图”（见图3—6（a）），在打开的窗口中加选“均值符号”及“均值连接线”，并再次“确定”，其操作见图3—6。

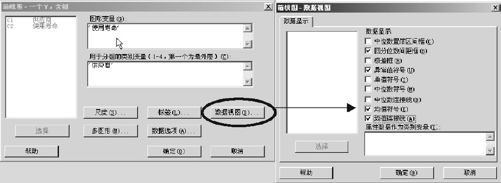
图3—6　增加箱线图功能的操作

再次操作后，将得到符合自己要求的图（见图3—7）。

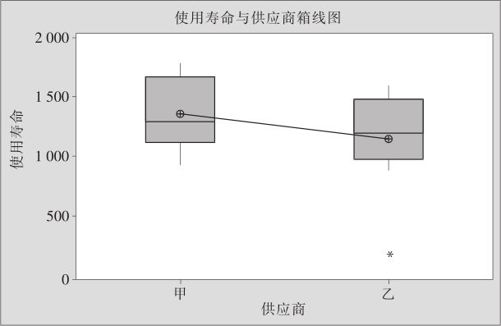
图3—7　增加箱线图功能的结果

上面通过增加图形功能的例题向大家展示了如何开发MINITAB软件所提供的丰富功能。本书中正式描述的操作都是能完成某个功能的最基本的操作，在界面上还有很多未提及的小窗口，大家可以打开尝试增加功能。这方面的内容丰富多彩，请大家在使用中学会完善功能，逐步提高使用MINITAB软件的水平。

3.3.3　饼图

饼图（pie chart）在显示属性统计资料的场合中使用最多。圆形中的各个不同大小和颜色的扇形代表不同的属性变量，它们的面积之和构成了一个完整的圆形，即代表所有属性变量的整体。这个特点非常适合体现某个整体的成分构成和各成分之间的对比关系。

制作饼图时，首先要画一个圆，其次根据各属性变量出现的频数f_i占总观测值数n的比率，计算出扇形度数θ_i＝f_i/n×360，然后以扇形度数为依据将圆周分割成一个个扇形，并添加不同的颜色和图例加以区分，最终绘制成简单易懂的饼图。

例3—5

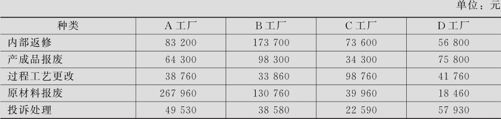
某集团公司下属四家工厂年终编写年度质量报告，汇总后得到当年的劣质成本金额数量，试绘制饼图分析（数据列在表3—4中，数据文件：BS_饼图.MTW）。

表3—4　全年劣质成本数据表

解　利用MINITAB的实现方法如下：

（1）选择“图形＞饼图（Graph＞Pie Chart）”中的“用整理好的表格画图（Chartvaluefromatable）”。

（2）指定“类别变量（Categoricalvariable）”为“种类”，指定“汇总变量（Sum-maryvariables）”为“金额”。

（3）在“饼图选项＞排列扇形区，按：（Pie Chart Options＞Order Slices By:）”中“选大小递减（decreasing volume）”，在“标签（Labels）”的“扇形区标签（Slice Labels）”中“选百分比（Percent）”，指定“多图形＞按变量＞按变量，组在相同图形中：（Multiple Graphs＞By Variables＞By variables with groups on same graph:）”为“工厂”，则可得到如图3—8所示的图形输出。

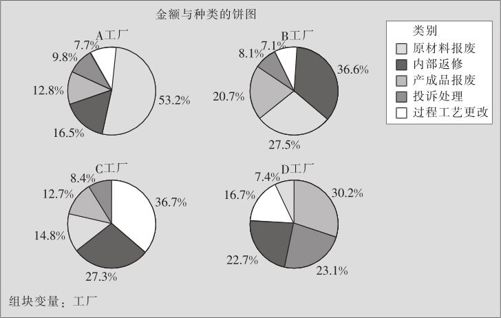
图3—8　饼图分析

从上图可以看出四家工厂劣质成本的构成比例各有不同，金额最高的劣质成本也各不相同，产生这些现象的具体原因值得进一步分析，例如使用列联表方法（详见6.3节）。

3.3.4　时间序列图

时间序列图（time series plot）是显示观察值随时间变化而不断变化的图形。在自然界和社会领域，客观现象发展变化的差异及其规律性可以通过时间变量反映时，往往会借助时间序列图来展现。

时间序列图有两个基本要素：时间要素和观察值要素。前者主要说明客观现象的观察值所属的时间类型及其长度，后者主要表明客观现象在某一时间点上发展变化的结果和状态。相对而言，观察值要素的作用更重要，对它的要求也更高。

制作时间序列图时，通常以时间为横坐标，以观察值为纵坐标，先按时间顺序依次描点，再用折线连接各点即可。

例3—6

某工厂成品仓库每月月末盘点记录产品的库存数量，试绘制时间序列图分析（数据列在表3—5中，数据文件：BS_时间序列图.MTW）。

表3—5　全年成品库存数据表

解　利用MINITAB的实现方法如下：

（1）选择“图形＞时间序列图（Graph＞Time Series Plot）”中的“简单（Simple）”。

（2）指定“序列（Series）”为“库存量”。

（3）在“时间／尺度（Time/Scale）”中选“时间＞时间尺度＞标记（Time＞Time Scale＞Stamp）”，指定“标记列（Stampcolumns）“为“月份”，则可得到如图3—9所示的图形输出。

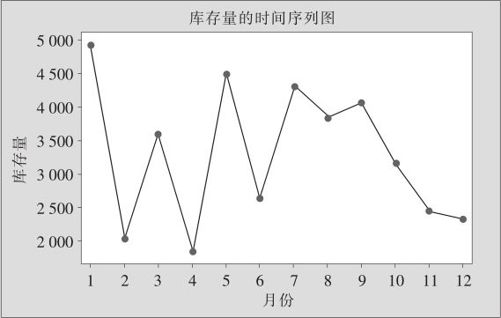
图3—9　时间序列图分析

从上图可以看出该厂成品库存的数量依托时间序列而表现出来的变化特点，其中上半年的波动范围较大，但下半年却呈显著递减趋势，暗示着某种积极因素在发挥作用。

3.3.5　3D散点图

散点图（scatterplot）是研究成对出现的两组数据之间相关关系的简单图示，它的实现方式相对比较容易，在此介绍更进一步的3D散点图（3D scatterplot），即可以研究成对出现的三组数据之间相关关系的三维立体图形。一个数据（X，Y，Z）就是三维空间中的一个点，很多个数据就构成了三维空间中的点集，观察点集的分布状态便可判别三组数据两两之间的相关程度，或是推断其中两组数据对另一组数据的影响程度。

制作3D散点图时，首先应建立与三组数据相对应的X轴、Y轴和Z轴，然后找出X，Y和Z的最大值和最小值，以这些值为参考界定三个坐标轴，并定义各个坐标轴的刻度，最后在这个三维坐标系中进行描点即可，必要时还可以画投影线。

例3—7

面包房制作某糕点时，为了解烘烤时间、烘烤温度与糕点口感（0分为最差，10分为最佳）的关系，特收集了一批过程数据，试绘制3D散点图分析烘烤时间与温度对糕点口感的影响（数据列在表3—6中，数据文件：BS_3D散点图.MTW）。

表3—6　糕点生产过程数据表

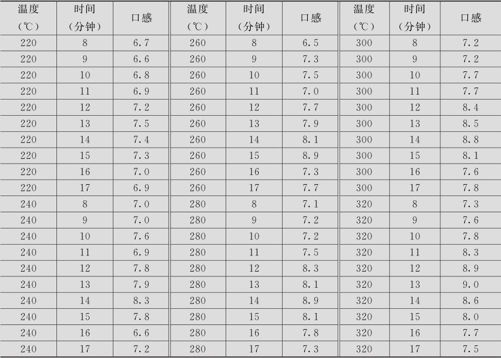
解　利用MINITAB的实现方法如下：

（1）选择“图形＞3D散点图（Graph＞3D Scatterplot）”中的“简单（Simple）”。

（2）指定“Z变量（Z variable）“为“口感”，“Y变量（Y variable）“为“温度”，“X变量（X variable）“为“时间”。

（3）在“数据视图（Data View）”的“数据显示（Data Display）”中选“投影线（Projectlines）”，则可得到如图3—10所示的图形输出。

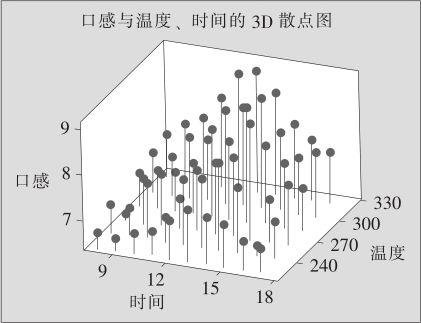
图3—10　3D散点图分析

从上图可以看出烘烤温度和时间对糕点口感都有显著的影响。一般来说，温度越高，口感越好；时间控制在12～15分钟区间内时，口感最好。此外，如果对3D散点图的三维立体效果不甚满意时，还可选择“工具＞工具栏＞3D图形工具（Tools＞Toolbars＞3D Graph Tool）”，用此工具栏上的按钮进行编辑处理。

3.3.6　3D曲面图

用于研究成对出现的三组数据之间相互关系的图形不是仅有3D散点图，3D曲面图（3D surface plot）是另一种能够达到此功效的图形表达形式。尤其是在探索如何用因素变量对响应变量构建一个合适模型的时候，它的作用特别突出。

与3D散点图类似，制作3D曲面图也需要有X，Y，Z三个轴。值得一提的是，图形中的曲面不是直接连接原始的数据点形成的一个曲面，而是首先基于原始的三维数据用插值法生成拟合Z值，然后再用X值、Y值和拟合Z值生成的一个平滑连续的曲面图。

例3—8

某炼钢厂的工艺部门已知加工温度和时间会对产成的钢铁的强度产生重要影响，为了进一步了解温度和时间影响钢铁强度的总体规律和趋势，收集了一批现场数据，试用3D曲面图进行探索性分析（数据列在表3—7中，数据文件：BS_3D曲面图.MTW）。

表3—7　钢铁生产过程数据表

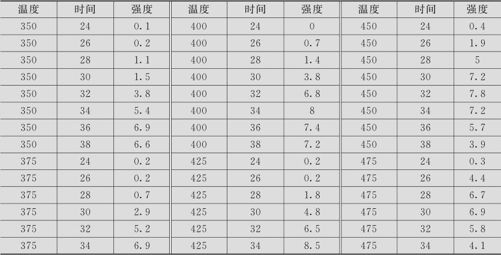
解　利用MINITAB的实现方法如下：

（1）选择“图形＞3D曲面图（Graph＞3D Surface Plot）”中的“曲面（Surface）”。

（2）指定“Z变量（Z variable）”为强度，“Y变量（Y variable）”为时间，“X变量（X variable）”为温度。

（3）在“数据视图（Data View）”的“数据显示（Data Display）”中选“曲面（Surface）”、“符号（Symbols）”和“投影线（Projectlines）”，则可得到如图3—11所示的图形输出。

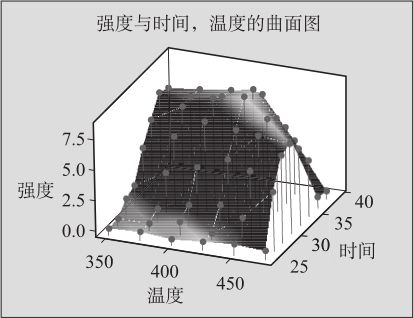
图3—113　D曲面图分析

从上图可以看出该曲面能够较好地表现温度和时间对钢铁强度的影响关系，强度实际值与拟合值的误差较小，值得用响应曲面分析（详见13.5节）的方法构建一个精确的模型并预测最优效果。同样，如果对图中的三维立体效果不甚满意时，也可用“工具＞工具栏＞3D图形工具（Tools＞Toolbars＞3D Graph Tool）”上的按钮进行编辑处理。

3.3.7　矩阵图

当我们需要研究的数据有4个、5个，乃至更多个变量时，3D散点图或3D曲面图也无法直接表达。这时候，矩阵图（matrix plot）就成了一个合适的图形工具。其实，矩阵图的全称是散点图矩阵图，它通过创建一个二维散点图阵列来同时评估多个变量对之间的关系。在数据变量较多时，分析效率会明显提高。

矩阵图中的每张子图都是反映任意两个变量关系的散点图，它有条理并紧凑地将所有二维散点图拼接在一起。对角线位置显示的是数据的变量名称，右上角部分与左下角部分其实是对称的，如果想简化图形可以省略不画。必要时还可以在所有的散点图上添加分组变量标记或者回归拟合线和平滑拟合曲线。

例3—9

某野生动物保护机构想研究黑熊的身体素质情况，通常在现场为熊称重的尺度使用起来很不方便，所以希望找到一些可用作体重指示器的更可靠、更简单的度量。因为不清楚哪些变量与体重密切相关，所以想创建一个矩阵图来确定各个度量之间的关系（数据列在表3—8中，数据文件：BS_矩阵图.MTW）。

表3—8　黑熊体型测量数据表

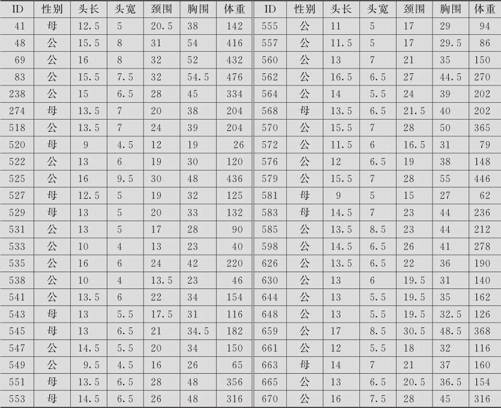
解　利用MINITAB的实现方法如下：

（1）选择“图形＞矩阵图（Graph＞Matrix Plot）”上半部分“图的矩阵（Matrixofplots）”中的“简单（Simple）”。

（2）指定“图形变量（Graph variables）”为头长、头宽、颈围、胸围、体重，则可得到如图3—12所示的图形输出。

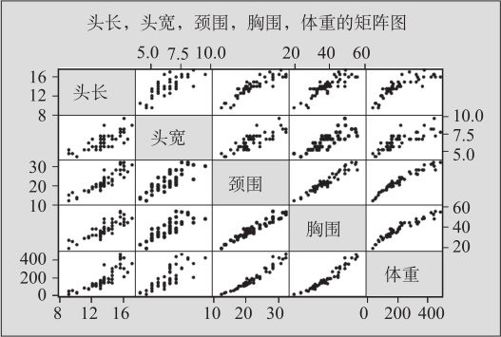
图3—12　矩阵图分析

从上图可以看出前4个度量都与黑熊的体重有一些正相关的关系，其中胸围和颈围与体重的相关性更加密切。此外，如果想观察不同性别的黑熊是否会有不同的体重指示器，可以选择“图形＞矩阵图（Graph＞Matrix Plot）”上半部分“图的矩阵（Matrix of plots）”中的“含组（With Groups）”进入操作；如果想观察体重指示器与体重的线性或非线性拟合效果，可以选择“图形＞矩阵图（Graph＞Matrix Plot）”上半部分“图的矩阵（Matrix of plots）”中的“包含平滑器（With Smoother）”进入操作。