12.3　计数控制图

一般对离散型随机变量所做的控制图，称为计数控制图。计数控制图是建立在二项分布B（n，p）或泊松分布P（λ）的理论基础上，由于二项分布和泊松分布各自的特征值均值和方差彼此相关、不独立，因此控制计数值的波动只需要一张控制图。计数控制图又要区分为两类，如果产品之检验结果只有两类：合格或不合格，这属于“计件”型，不合格产品数X肯定会小于总检查产品数n，且不合格产品数服从二项分布B（n，p），这要用监控不合格数的NP控制图，或监控不合格率的P控制图。另一种情况则是缺陷点的“计点”型，例如每天检查6片芯片，共有13个瑕疵点，瑕疵点个数服从平均值为λ的泊松分布，这要用监控缺陷数的C控制图，或监控单位产品上的平均缺陷数的U控制图。

关于各种类型的计数控制图的统计基础，现已整理为表12—4。这里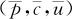是从实测数据估计而得的相应平均值。

表12—4　计数控制图的统计基础

计数控制图的制作步骤与计量控制图类似。本节将通过4个案例，逐一介绍常见计数控制图的实现方法。

例12—2

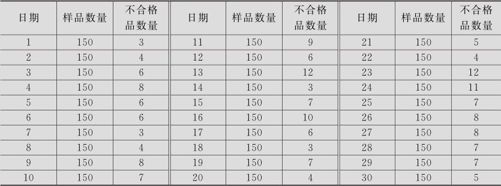
在二极管生产线上，于每个班次结束前抽取150个二极管进行检验。下面是6月份共计30个工作日每天的不合格二极管数量的记录。试绘制一个控制图来分析产品的不合格品率是否稳定（数据列在表12—5中，数据文件：SPC_二极管不合格品率.MTW）。

表12—5　6月份二极管的抽样结果

解　计算机软件MINITAB的实现方法如下：

1．从“统计＞控制图＞属性控制图＞P（Stat＞Control Charts＞Attributes Charts＞P）”进入。

2．指定“变量（Variables）”为“不合格品数量”，“子组大小（Subgroup sizes）”为“样品数量”，运行命令后得到P控制图（见图12—6）。

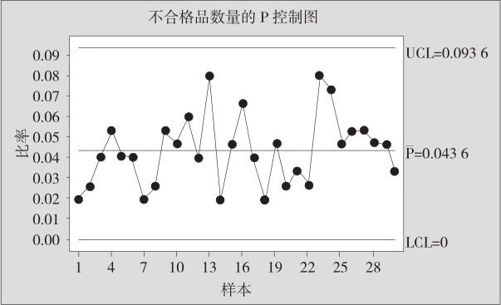
图12—6　6月份二极管不合格品数量的P控制图

由图12—6可知，P控制图中的所有数据点都未违背任何一条判异准则，整个过程的不合格品率非常稳定，二极管的生产处于统计控制状态。由于这里的样品数量是固定的常数“150”，因此也可以换成监控其不合格品数的NP控制图，其监控效果与P控制图完全相同，只是控制图中的纵坐标由不合格品率换成不合格品数罢了。

计算机软件MINITAB的实现方法如下：

1．从“统计＞控制图＞属性控制图＞NP（Stat＞Control Charts＞Attributes Charts＞NP）”进入。

2．指定“变量（Variables）”为“不合格品数量”，“子组大小（Subgroup sizes）”为“样品数量”，运行命令后得到NP控制图（见图12—7）。

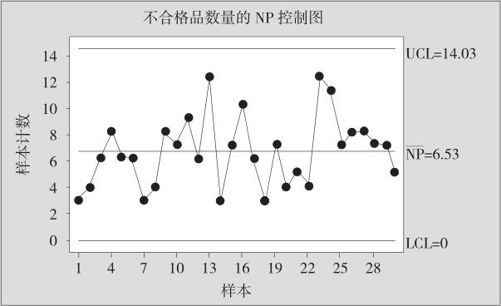
图12—7　6月份二极管不合格品数量的NP控制图

例12—3

在二极管生产线上，于每个班次结束前抽取数量不等的二极管进行检验。下面是12月份共计30个工作日每天的不合格二极管数量的记录。试绘制一个控制图来分析产品的不合格品率是否稳定（数据列在表12—6中，数据文件：SPC_二极管不合格品率2.MTW）。

表12—6　12月份二极管的抽样结果

解　由于每日抽取进行检验的二极管数量不等，因而不能使用NP图。我们用P图进行生产的监控。绘制P图的计算机软件MINITAB实现方法如下：

1．从“统计＞控制图＞属性控制图＞P（Stat＞Control Charts＞Attributes Charts＞P）”进入。

2．指定“变量（Variables）”为“不合格品数量”，“子组大小（Subgroup sizes）”为“样品数量”，运行命令后得到P控制图（见图12—8）。

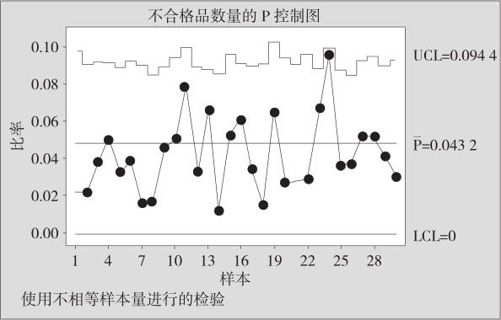
图12—8　12月份二极管不合格品数量的P控制图

由图12—8可知，虽然每天的抽检数量不同，上控制限变成了“城墙”形状，但二极管的生产仍处于统计控制状态。

有实际工作经验的人都会明白，如果控制图的样式如图12—8所显示那样，使用起来是很不方便的，而且此种“城墙”状控制图只能在分析用控制图中使用。为此，我国的国家标准（GB/T4091－2001）规定：“如果子组大小变化不大，则可以采用单一的基于平均子组大小的一组控制限。实际上，当子组大小的变化在子组大小目标值的±25％以内时，可采用上述方法。”“当子组大小变化较大时，可采用另一种利用标准化变量的方法。”

上面讨论过的NP控制图及P控制图都是针对“计件”型产品而制定的，产品检验结果只有两类：合格或不合格。总检查产品数n及不合格品率给定时，不合格产品数X服从二项分布B（n，p）。另一种情况则是缺陷点的“计点”型，缺陷点个数X服从平均值为λ的泊松分布，抽样调查的样本中很可能出现缺陷点个数超过检验样品数的情况。例如检查了4个电镀件，共出现了9个斑点。这时监控生产可以有两种控制图：监控缺陷数的C控制图；监控单位产品上的平均缺陷数的U控制图。下面分别举例予以介绍。

例12—4

在芯片的生产过程中，如果芯片上有一个瑕疵点，则认为是一个缺陷，每个班次结束前抽取10片芯片进行检验。下面是3月份前15个工作日每天总缺陷数情况的记录。试绘制一个控制图来分析产品的缺陷数是否稳定（数据列在表12—7中，数据文件：SPC_芯片缺陷率.MTW）。

表12—7　3月份芯片的抽样结果

解　先介绍监控单位产品上的平均缺陷数的U控制图。计算机软件MINITAB的实现方法如下：

1．从“统计＞控制图＞属性控制图＞U（Stat＞Control Charts＞Attributes Charts＞U）”进入。

2．指定“变量（Variables）”为“缺陷数”，“子组大小（Subgroup sizes）”为“样品数量”，运行命令后得到U控制图（见图12—9）。

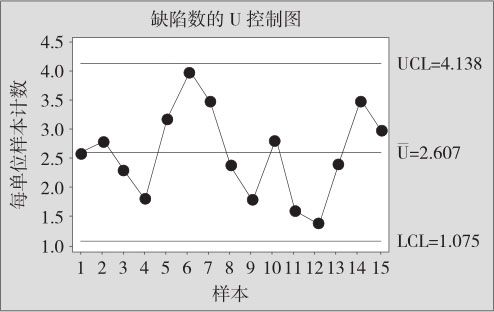
图12—9　3月份芯片缺陷数的U控制图

由图12—9可知，U控制图中的所有数据点都未违背任何一条判异准则，整个过程的缺陷率非常稳定，芯片的生产处于统计控制状态。由于这里的样品数量是固定的常数“10”，所以也可以换成监控其总缺陷数的C控制图，其监控效果与U控制图完全相同，只是控制图中的纵坐标由平均缺陷数换成总缺陷数罢了。

计算机软件MINITAB的实现方法如下：

1．从“统计＞控制图＞属性控制图＞C（Stat＞Control Charts＞Attributes Charts＞C）”进入。

2．指定“变量（Variables）”为“缺陷数”，运行命令后得到C控制图（见图12—10）。

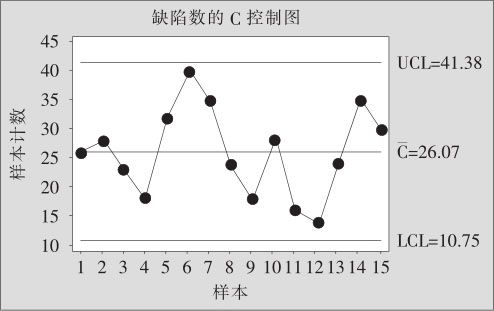
图12—10　3月份芯片缺陷数的C控制图

例12—5

在芯片生产过程中，每个班次结束前抽取一定数量的产品进行检验。下面是9月份前15个工作日每天的有缺陷芯片情况的记录。试绘制一个控制图来分析产品的缺陷率是否稳定（数据列在表12—8中，数据文件：SPC_芯片缺陷率2.MTW）。

表12—8　9月份芯片的抽样结果

解　由于每天检测的样品数量是不同的，因此只能使用U控制图。计算机软件MINITAB的实现方法如下：

1．从“统计＞控制图＞属性控制图＞U（Stat＞Control Charts＞Attributes Charts＞U）”进入。

2．指定“变量（Variables）”为“缺陷数”，“子组大小（Subgroup sizes）”为“样品数量”，运行命令后得到U控制图（见图12—11）。

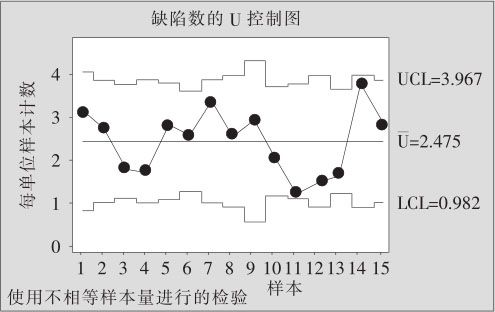
图12—11　9月份芯片缺陷数的U控制图

由图12—11可知，虽然每天的抽检数量不同，上、下控制限变成了“城墙”形状，但芯片的生产仍处于统计控制状态。当下限计算为负值时，计算机将自动把它修正为0，这样一来下限就变成LCL＝0的水平线了。图12—8的P图与此类似，它已变为LCL＝0了。