12.6　过程能力分析

在用控制图确认过程处于统计控制状态之后，可以进行过程能力分析，进一步判断过程能力是否达到顾客的要求。过程能力分析也是六西格玛项目中评价过程基线和改进方向的重要工具。过程的数据类型分为计量数据和计数数据两类，过程能力分析的方法也要分为两类。

12.6.1　计量数据的过程能力分析

通过比较过程公差限的宽度和过程度量值的变化宽度，计算其比值，可以评价过程满足顾客要求或工程规范的能力。当产生计量数据的过程稳定且输出服从正态分布时，如果分布的总体标准差σ已知，可按下列数学公式分别进行过程能力指数C_p与C_pk以及过程绩效指数P_p与P_pk的计算和分析（见图12—29）。

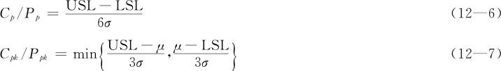
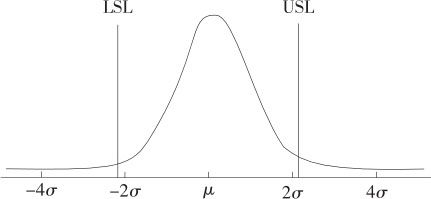
图12—29　过程能力分析示意图

由于总体标准差σ通常是未知的，因此必须使用实测样本对它进行估计后才能得出相应的样本统计量。如果强调的是从过程固有波动的角度来考察过程能力，其中的固有波动6σ主要由随机因素的影响而产生，对于划分子组的过程，其变化宽度值用控制图中的6/d₂来估计；对于不划分子组的过程，观测值是单值，只要将上式中的平均极差换成平均移动极差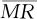即可，这时，过程能力指数记为C_p与C_pk，也称短期能力指数。如果强调的是从过程总波动的角度考察过程能力，其中的总波动6σ由随机因素和特殊因素的共同影响而产生，其变化宽度值用样本整体的标准差6S来估计，这时过程绩效指数记为P_p与P_pk，也称长期能力指数。

显然，所有这些指标的数值越大，标志着过程能力越好。随着时代的发展，对这些指标的要求也越来越高。例如，在传统的质量标准中，C_p＞1（公差超过6倍σ）表明过程能力尚可。但用高标准的六西格玛眼光来看，C_p≥2（公差超过12倍σ）的过程才是理想的过程。

至于在计算C_p和P_p的同时还要计算C_pk和P_pk的原因是：C_p和P_p是假定过程输出的均值与目标值重合时的过程能力，只反映了过程的潜在能力。但对大多数情况来说，过程输出的均值与目标值不重合。因此，引入C_pk和P_pk的目的就是将均值偏移的影响也考虑进来。在实际工作中，应当同时考虑这两类指数，以便对整个过程的状况有较全面的了解。显然，当过程的实际中心与公差中心重合时，C_pk和P_pk的数值一定会与C_p和P_p相等。当C_pk/P_pk的数值与C_p/P_p越接近时，说明过程的实际中心离公差中心越近；反之，当C_pk/P_pk的数值离C_p/P_p越远时，则说明过程的实际中心偏离公差中心越远。正是由于这个性质，可以从C_p/P_p及C_pk/P_pk这一对数值的状况清楚地看出过程的状况及过程应改进的方向。例如，当C_pk/P_pk的数值与C_p/P_p很接近，但数值都还偏小（例如C_p＝0.9，C_pk＝0.8），则说明过程的实际中心离公差中心不远，问题的关键是生产过程的波动太大，降低标准差是关键；反之，当C_pk/P_pk的数值与C_p/P_p相差悬殊，但C_p/P_p还算满意（例如C_p＝1.5，C_pk＝0.9），则说明生产过程的波动尚可，但是实际中心离公差中心较远，问题的关键是要将生产过程的实际中心调整至公差中心处。总之，要结合C_p/P_p与C_pk/P_pk的搭配才能清楚地看出过程的全面状况。

从统计学的角度看长期或短期的能力的差别，其实只是总体标准差σ的估计方法不同而已。因此，当生产过程只有随机误差的波动时，两者的数值应该相差不大，哪个稍大哪个稍小完全是随机的，不能完全确定；当生产过程除了含有随机误差的波动，还含有明显的组间差异时，两者的数值应该相差悬殊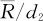，用（或用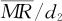）来估计出的σ比用整体s估计出来的σ要小很多，因而短期能力指数将比长期能力指数大很多。因此，在实际问题中，如果发现短期能力指数与长期能力指数相差不多时（不论谁大谁小），就可以肯定，生产过程中只受到随机误差波动的影响；如果发现短期能力指数比长期能力指数大很多时，就可以肯定，生产过程中除了受到随机误差波动的影响，组间差异的影响是非常显著的。

过程能力的另一个常用指数是C_pm。当生产过程不但给出上下公差限，而且给出过程的目标值m时，可以用C_pm表示过程能力：

式中

很明显，当过程的实际中心μ与过程目标值m重合时，C_pm的数值一定会与C_p/P_p相等。当C_pm的数值与C_p/P_p越接近，则说明过程的实际中心与过程目标值m越接近；反之，当C_pm的数值与C_p/P_p相比越小，则说明过程的实际中心与过程目标值m越远。与C_pk/P_pk不同的是，C_pk/P_pk反映的是实际中心μ离公差限中心值的偏离程度，而C_pm的应用则可以更广泛些，这里可以指定任意值作为过程目标。

描述过程能力的另一个常见的指数是“偏离指数”。由前可知，当过程均值与公差中心重合时，C_pk＝C_p；当过程均值与公差中心不重合时，C_pk＜C_p，而且偏离越严重时二者相差越大。根据这个性质，很容易想到一个量，我们称K为偏离指数，有

当过程均值与公差中心重合时，K＝0；当过程均值与公差中心不重合时，K＞0；即K总是一个正数，K越大表示偏离越严重。如果K达到1，则说明C_pk＝0，即过程均值偏离到正好等于上（或下）公差限。如果K＞1，表明C_pk＜0，即过程均值偏离到上（或下）公差限之外了，通常这种情况可以不在我们讨论范围内。

结合式（12—7）和式（12—10）两个定义，如果公差中心记为T，半公差限记为R，则容易得到偏离指数K的另一个等价定义：

这样一来，偏离指数K的含义就更直观了，它是偏离量与半公差限之比（见图12—30）。

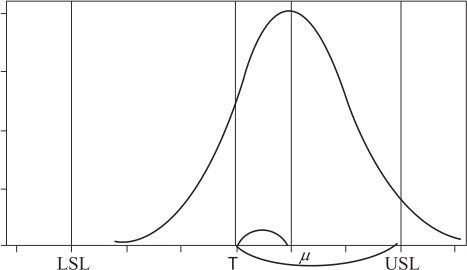
图12—30　过程的偏离指数K的示意图

前面讲过，单独一个指数，例如C_p或C_pk都不能全面描述过程能力的状况，但二者的组合（C_p，C_pk）则可以全面描述过程的状况。同样，（C_p，C_pm）也是可以全面描述过程的状况的一对指标。在增加了偏离指数K之后，（C_p，K）也是可以全面描述过程的状况的一对指标。具体使用哪一对指标作为过程能力的描述依赖不同的场合，可能各有各的特点，但从数学上说，这三对的含义和价值都是相同的。

下面用例12—11对计量数据的过程能力分析的实际应用加以说明。

例12—11（续例12—1）

在钢珠生产过程中，假定顾客允许的钢珠直径的变异范围为［10.90，11.00］，试进行过程能力分析（数据列在表12—3中，数据文件：SPC_钢珠直径.MTW）。

解　计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞能力分析＞正态（Stat＞Quality Tools＞Capability Analysis＞Normal）”进入。

2．指定“单列（Single column）”为“直径”，指定“子组大小（Subgroup size）”为“批次”，在“规格下限（Lower spec）”中输入“10.90”，在“规格上限（Upper spec）”中输入“11.00”。

3．打开“选项（Options）”，在“目标（添加C_pm到表格）”中输入过程的目标值“10.95”。运行命令后得到图12—31。

观察图12－31，可以获得很多信息。首先，图正中带两条拟合曲线的直方图给了我们最直观的认识。两条线几乎完全重合，将左上角的标准差（组内）＝0.0252228与标准差（整体）＝0.024645相比，相差甚微，这都说明，除组内随机误差外，组间差的差异是不显著的。其次，C_p＝0.66，C_pk＝0.66，两者均小于1，说明过程能力不足，两者没有差别，说明改进过程时，主要改进方向是设法降低过程的波动。再次，P_p＝0.68，P_pk＝0.67，两者均近似于C_p与C_pk，说明当前的过程能力非常接近过程固有的能力，过程中不存在组间差异过大的特殊因素，应当从寻找随机因素入手提高过程能力。此外，图左下方的PPM值的统计从可能出现的不良率这个角度解释了过程能力的优劣。

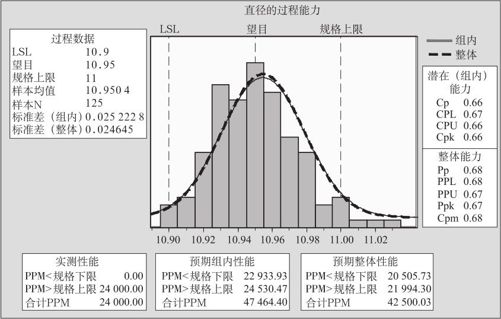
图12—31　计量数据的过程能力分析

另外要注意的是，在进行上述分析之前，先应该验证过程是稳定的，还应该验证过程服从正态分布，才能进行过程能力的计算。为了简化这一分析过程，计算机软件MINITAB提供了另一个窗口“六合一”的一条龙式的全流程：Capability Sixpack。具体的实现方法如下：

1．从“统计＞质量工具＞Capability Sixpack＞正态（Stat＞Quality Tools＞Capability Sixpack＞Normal）”进入。

2．指定“单列（Single column）”为“直径”，指定“样本大小（Subgroup size）”为“批次”，在“规格下限（Lower spec）”中输入“10.90”，在“规格上限（Upper spec）”中输入“11.00”。

3．打开“选项（Options）”，在“目标（添加C_pm到表格）”中输入过程的目标值“10.95”，运行命令后得到图12—32。

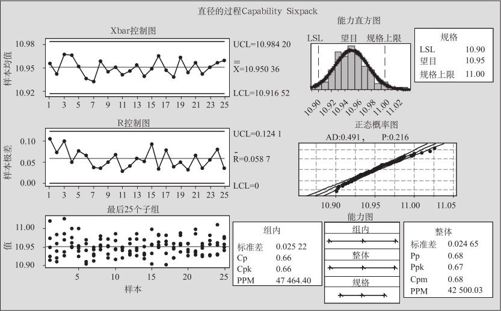
图12—32　过程能力的Capability Sixpack分析

图12—32蕴含着非常丰富的信息。首先，左上的Xbar控制图、左中的R控制图以及左下最后25个子组的散点图可以用来验证过程是否稳定。其次，右上的能力直方图和右中的正态概率图可以用来验证过程是否服从正态分布。此外，右下的能力图精确地显示出过程能力指数及其置信区间。

12.6.2　计数数据的过程能力分析

对于输出特性为计数数据的过程，也需要进行过程能力分析。数据分布的类型不同（Poisson分布和二项分布），过程能力的估算方法也有所不同。对于二项分布的过程绩效指标主要用百万机会缺陷数DPMO，可以由此算出缺陷率p，查标准正态分布的上侧概率表（见附表2）即可求得西格玛水平Z值。详细步骤可以参看例12—13。对于Poisson分布的过程绩效指标则略有不同，有单位缺陷数DPU、直通率YFT、缺陷率p和西格玛水平Z等几个指标，下面先列出主要的计算公式以说明过程绩效指标的计算方法和相互关系，详细步骤可以参看例12—12。

式中，D为缺陷数；U为单位数；Φ^－1（）为逆累积标准正态概率函数。

例12—12

某电话分局最近一个月（30天）内共发生接错电话事故4次，试以日为单位计算电话接线过程的西格玛水平Z。

解　容易得到单位缺陷数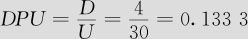。但由于4次接错电话事故不一定恰好在不同的4天之内，因此以天为单位计算“不良”，并不能断言不良率为13.33％，而应该按Poisson分布以式（12—10）至式（12—13）来计算。根据式（12—11），得知直通率Y_FT＝e^-DPU＝e^－0.1333＝87.517％，那“一天内无任何接错电话事故”的概率为87.517％（比1－13.33％＝86.67％要稍大一些）。不良率（一天中至少有一次接错电话事故的概率）为p＝1－87.517％＝12.483％（比13.33％要稍小一些）。

计算西格玛水平的公式是：Z＝Φ^－1（Y_FT）＝Φ^－1（87.517％）＝1.15118。其操作是：从“计算＞概率分布＞正态分布（Calc＞Probability Distributions＞Normal Distribution）”入口，选中“逆累积概率（Inverse cumulative probability）”，在“输入常量”格内，输入常数“0.87517”（参见图4—4），即可得到结果“1.15118”。手边无计算机时，也可以将0.87517代入标准正态分布函数表（见附表1）反查，或将不良率0.12483代入正态分布上侧概率表（见附表2）反查，都可以得到相应Z值近似为1.15。

下面对二项分布的计件数据的过程能力分析用例12—13加以说明。

例12—13（续例12—2）

试对二极管生产线的状况进行过程能力分析（数据列在表12—5中，数据文件：SPC_二极管不合格品率.MTW）。

解　计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞能力分析＞二项（Stat＞Quality Tools＞Capability Analysis＞Binomial）”进入。

2．指定“缺陷数（Defectives）”为“不合格品数量”，“实际样本量（Use sizes in:）”为“样品数量”，运行命令后得到图12—33。

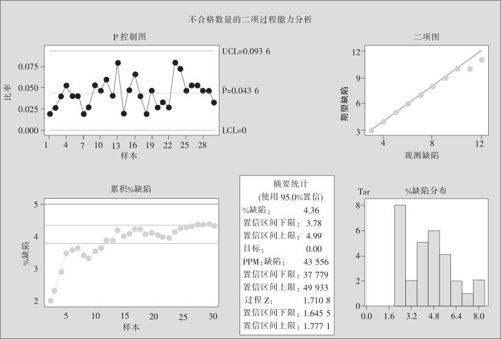
图12—33　计数数据的过程能力分析

观察图12—33，可以获得很多信息。首先，图中左侧的P控制图和累积不良品率图表明过程处于统计受控状态。其次，图中右侧的二项分布概率图和不良品率的直方图表明过程的输出数据服从二项分布。最后，图中下方的摘要统计显示，过程绩效指标为43556ppm，缺陷率p＝4.36％，西格玛水平Z＝1.7108，以及各自的置信区间。显而易见，如果用六西格玛的标准（DPMO＝3.4ppm，Z＝4.5）来衡量，该过程的能力指标还是比较低的。

由于不良品率与西格玛水平的换算经常要进行，MINITAB软件的输出常常同时给出两个值，具体计算步骤如例12—12所述。本书后的附表2也给出了对应数值表。例如例12—13中，不良品率p＝4.36％，按0.0436查附表2，则可得到西格玛水平Z＝1.71。对于更小的不良品率也可以很清楚地查出来，例如，不良品率为30ppm，写成0.000030＝0.0⁴30，查附表2可得知Z＝4.01。

12.6.3　非正态数据的过程能力分析

当需要进行过程能力分析的计量数据呈非正态分布时，直接按12.6.1节中介绍的方法处理会有很大的风险。一般解决方案的原则有两大类：一类是设法将非正态数据转换为正态数据，然后就可按正态数据的计算方法进行分析；另一类是根据以非参数统计方法为基础，推导出一套新的计算方法进行分析。遵循这两大类原则，在实际工作中成熟的实现方法主要有三种，现在简要地介绍每种方法的操作步骤。

第一种方法是Box-Cox变换法。

（1）估计合适的Lambda（λ）值；

（2）计算求出变换后的数据y^*；

（3）根据原来给定的USL和LSL，计算求出变换后的USL和LSL；

（4）对y用USL和LSL^*求出过程能力指数。

第二种方法是Johnson变换法：

（1）根据Johnson判别原则确定转换方式；

（2）计算求出变换后的数据y^*；

（3）计算求出变换后的USL和LSL；

（4）对y用USL和LSL^*求出过程能力指数。

第三种方法是非参数计算法：

当第一、二种方法无法适用，即用Box-Cox法和Johnson法均无法找到合适的转换方法时，还有第三种方法可供尝试，即以非参数方法为基础，不需对原始数据做任何转换，直接按以下数学公式就可以进行过程能力指数C_p与C_pk的计算和分析。

式中，x_α是数据X分布的α分位数，例如x_0.005表示随机变量X分布的0.005（即0.5％）分位数。

例12—14（续例12—8）

假定质量标准允许的杂质含量的上限为24，已知其数据分布不正态，试进行过程能力分析（数据列在表12—13中，数据文件：SPC_Box Cox变换.MTW）。

解　从例12—8的计算结果中可以得知，Box-Cox变换所取λ＝0为最好，也即是要对杂质率取自然对数。将杂质率取自然对数后的值记录在原来文件中，然后就可以得到计算结果。其计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞能力分析＞正态（Stat＞Quality Tools＞Capability Analysis＞Normal）”进入。

2．指定“单列（Single Column）”仍为“杂质含量”，指定“子组大小（Subgroup size）”仍为“5”，在“规格上限（Upper spec）”中输入“24”，在“Box-Cox”中指定取λ＝0，在“选项（Option）”中设定“目标（Target）”为“10.95”，即可得到如图12—34所示结果。

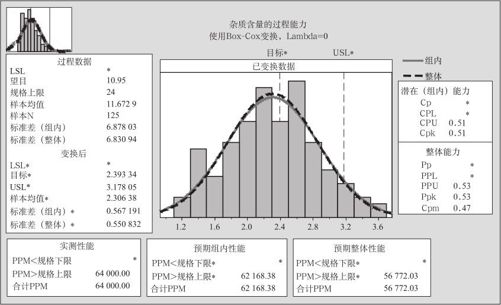
图12—34　Box-Cox变换法的过程能力分析

本例由于数据量足够，因此也可以使用非参数计算法，可将数学公式编写成宏指令ncap，供需要时调用，其调用格式是：

％ncap　X　USL　LSL

关于宏指令的具体内容，请参阅本书的5.6节，在此不再赘述。对于只有单侧公差限时，调用上述宏指令时，仍然要补充任一数以填写成两个限都存在的形式。命令如下：

％ncap　C1　24　0

输出结果中只有下列这一行是有意义的：

数据显示

下面简要介绍Johnson变换法的基本原理，并重点用案例说明使用此方法实现非正态数据过程能力分析的过程。

Johnson变换体系一般将连续数据分成三大数学类型，每个类型分别对应不同的转换公式。

第一种，SB分布类型，变换公式为：

第二种，SU分布类型，变换公式为：

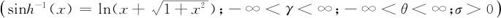
第三种，SL分布类型，变换公式为：

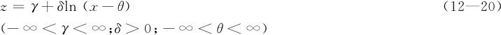
具体的模型判别和参数估计比较复杂，有兴趣的读者可以参阅参考文献［27］：邹远敏、波兰斯基和马森（Y. Chou，A. M. Polansky and R. L. Mason）的论文。通过相应的统计原理和实践检验可以证明，经Johnson转换后计算所得的过程能力指数与实际值的拟合度很高，即误差很小。

例12—15（续例12—8）

假定质量标准允许的杂质含量的上限为24，已知其数据分布不正态，试进行过程能力分析（数据列在表12—13中，数据文件：SPC_Box Cox变换.MTW）。

解　计算机软件MINITAB的实现方法如下：

1．从“统计＞质量工具＞能力分析＞正态（Stat＞Quality Tools＞Capability Analysis＞Normal）”进入。

2．指定“单列（Single column）”为“杂质含量”，指定“子组大小（Subgroup size）”为“5”。打开“变换（Transformation）”，选择“Johnson转换（Johnson transformation）”，在“规格上限（Upper spec）”中输入“24”，运行命令后得到图12—35。

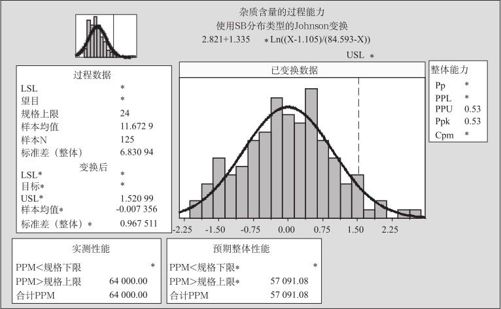
图12—35　Johnson变换法的过程能力分析

观察图12—35，同样可以获得很多信息。首先，图正中带拟合曲线的直方图是经Johnson转换后的过程数据，与左上方表示原始数据的带拟合曲线的直方图相比，正态性明显好转。其次，转换所采用的公式为图上方所示：

2.821＋1.335ln［（X－1.105）/（84.593－X）］

再次，从两边的及下边的数据表格中可以看到，USL^*＝1.52099，P_pk＝0.53，合计ppm＝57091.08。显然，该过程的过程能力不高，很有改进的必要。另外也可以看出，使用非参数方法与经Box-Cox变换或Johnson变换后的计算结果相差不多，二者不需要很大样本量，而使用非参数方法需要样本量要大得多。