13.5　响应曲面设计

13.5.1　响应曲面设计概论

在实际工作中，常常需要研究响应变量Y究竟如何依赖于自变量，进而能找到自变量的设置使得响应变量得到最佳值（望大、望小或望目）。如果自变量的个数较少（通常不超过3个），则响应曲面方法（response surface methodology，RSM）是最好的方法之一。本方法特别适合于响应变量望大或望小的情形，如果问题是望目的情形，虽然用全部重复响应曲面试验的方法也能解决，但参数稳健设计（robust parameter design）方法则更适合于响应变量望目的情形。

通常的做法是：先用2水平的因子试验的数据，拟合一个线性回归方程（可以含交叉乘积项），如果发现有弯曲的趋势，则希望拟合一个含二次项的回归方程。其一般模型是（以两个自变量为例）：

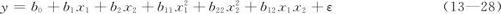
这些选项比因子设计的模型增加了各自变量的平方项。由于要估计这些项的回归系数，原来因子设计所安排的设计点就不够用了，要再增补一些试验点。这种先后分两阶段完成全部试验的策略就是“序贯试验”的策略。适用于这种策略的方法有很多种，其中最常用的就是中心复合设计（central composite design，CCD）。

13.5.1.1　中心复合设计

图13—49就是三维空间（即3个因子）中的一个中心复合设计示意图。

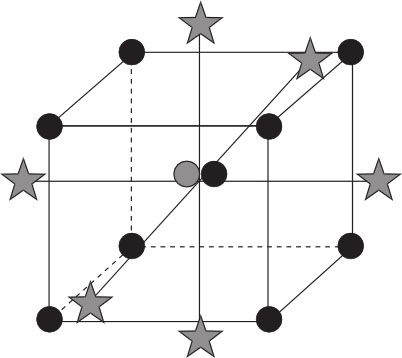
图13—49　3因子中心复合设计布点示意图

以下叙述中给出的坐标都假定各因子已代码化。

整个试验由下面三部分试验点构成：

（1）立方体点（cube point）（或角点（corner point）），各点坐标皆为1或－1，这就是组成因子试验的部分。

（2）中心点（center point），各点之各维坐标皆为0。

（3）星号点（star point）（或轴点（axial point））。除一个自变量坐标为±α外，其余自变量坐标皆为0。在k个因子情况下，共有2k个星号点。

上述立方体点和部分中心点构成本章13.3节中介绍过的一个普通的全因子设计，星号点和另一些中心点将其扩展为2阶设计。当然，如果可以肯定试验区域已接近于最优区域，则不必经过序贯试验，而直接进行中心复合设计，3部分试验点同时进行。这里有三个问题需要仔细讨论：

（1）如何选择全因子设计部分；

（2）如何确定星号点的位置（即确定α的数值问题）；

（3）如何确定中心点的个数问题。

在因子设计部分，通常都取全因子试验的安排方法，当因子个数大于5时才考虑部分因子设计，这时通常要求设计的分辨度在Ⅴ以上。

在α的选取上可以有多种出发点，旋转性（rotatability）是个很有意义的考虑。所谓旋转性指的是：将来在某点处预测值的方差仅与该点到试验点中心的距离有关，而与其所在方位无关，也即响应变量的预测精度在以设计中心为球心的球面上是相同的。可以证明，为了满足旋转性的要求，这时α值应取

式中，F代表因子试验点的总数。当因子试验选择了对k个因子的全因子试验时，则有

（当k＝2，α＝1.414；当k＝3，α＝1.682；当k＝4，α＝2；当k＝5，α＝2.378）

对于α值的选取其实不必很精确，设计只要有近似旋转性（near rotatability）就够了。按上述公式选定的α值来安排CCD设计是最典型的情形，它既可以满足旋转性，也可以同时实现试验的序贯性，此种试验特称中心复合序贯设计（central composite circumscribed，CCC），它是CCD中最常用的一种。

如果要求进行CCD设计，但又希望试验水平安排不能超过立方体边界时，可以将星号点设置为±1，则计算机会自动将原CCD缩小到整个立方体内，这种设计也称为中心复合有界设计（central inscribed design，CCI），但这种设计失去了序贯性，因为前一次在立方体点上已经做过的试验结果，在后续的CCI设计中已经没有用了。

带区组的CCD设计中，对于α值的选取就要从另一个角度出发了。由于把区组也作为一个因子（它是可控的，但它又是“讨厌因子”）来安排，在最开始估计各项效应显著性时，要把“区组”作为一个因子放入回归方程以减小误差，从而增加参数估计及判定的精度；但后来在作预报时，又应将“区组”这个因子从回归方程中删除。此时首先考虑的是，希望在“保留”和“删除”区组因子这两种不同选择下，对其他因子效应的估计要保持不变，也就是说，要保持“区组”因子与其他因子间效应估计的独立性或这两部分因子间的正交性。为此，我们要调整α值的选取标准，这时顾及不到旋转性而只能顾及正交性的要求了。具体的计算公式这里不详细叙述，计算机会自动按正交性的要求对不同的因子个数计算出相应的α值来。

对于α值的选取的另一个出发点也是有意义的，就是取α＝1。这就意味着将星号点的位置向中心收缩而设在立方体的表面上，这样的设计称为中心复合表面设计（central composite face-centered design，CCF）。这样做的另一个好处是每个因子取值的水平数只有3个（－1，0，1）；而一般的CCD，因子取值的水平数是5个（－α，－1，0，1，α），这在更换因子水平较困难的情况下是有意义的。另一种情况下也将有用：如果希望试验设计有序贯性，即允许先进行因子设计，其结果在2阶回归中仍然要采用，做CCF就是有意义的，但CCF的代价是失去了旋转性。其示意图见图13—50。

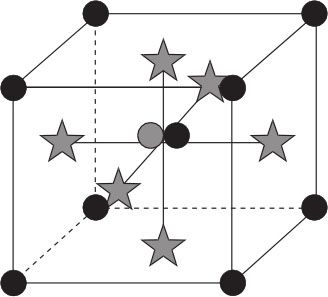
图13—50　3因子中心复合表面设计布点示意图

在中心点的个数（number of center，Nc）问题上，更是有很多细节要分析。在满足旋转性的前提下，如果再适当选择Nc，则可以使在整个试验区域内的预测值都有一致均匀精度（uniform precision）。这当然是好事。特别是在试验前，我们无法预知最优点究竟位于何处，在整个试验区域内的预测值都有一致均匀精度很重要，如果中心点重复得过少，则在试验接近中心的区域内之预测精度反而较低。为此，中心点的试验要重复很多次，具体次数见表13—26。但有时认为，这样做的代价太大，Nc其实取2以上就够了；如果安排中心点的目的主要是估计试验误差，则可能需要Nc取4以上。

表13—26　CCD设计试验点数表

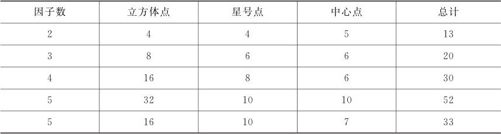
下面是一致均匀精度的CCD设计在不同因子数的情况下，博克斯所建议的各类型试验点的个数表（见表13—26）。

在表13—26中前3行（因子个数不超过4）的设计方案是唯一的；当因子个数为5时，有两种选择，前一种在因子点上进行的是全因子试验2⁵，而后一种是进行的部分因子试验2^5－1，相应的中心点个数要求也不同。

总之，当时间和资源条件都容许时，进行CCD试验设计时尽量按照表13—26中所给出的试验计划去安排试验，可以达到一致均匀的精度，设计结果和推测出的最佳点都比较可信。实在需要减少试验次数时，中心点至少也要2～5次。当因子水平更换有困难且试验水平安排不能超过立方体边界时可采用CCF设计。必须要保证一致均匀精度时，只能牺牲序贯性而保持旋转性，这时可以采用CCI设计。这些对于具体问题的处理原则将会在响应曲面设计的计划阶段体现出来。

13.5.1.2　Box-Behnken设计

响应曲面设计的另一种方法就是Box-Behnken设计。这种设计安排是将因子各试验点取在立方体的棱的中点上。3因子的Box-Behnken设计取点示意图见图13—51。

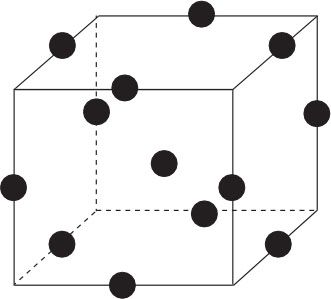
图13—51　3因子Box-Behnken设计取点示意图

这种设计所需点数比CCD要少，它也具有近似旋转性，它最适应的试验区域是球形域（而不是立方体域），它特别适合于立方体顶点无法获得数据时使用。但其最大缺点是设计没有序贯性，上批进行过的试验结果数据对下批试验几乎没有用，每批试验都要全部重新做。因子个数为3时，试验次数为12＋3＝15；因子个数为4时，试验次数为24＋3＝27。除非极端重视试验次数，否则通常不采用这种设计。

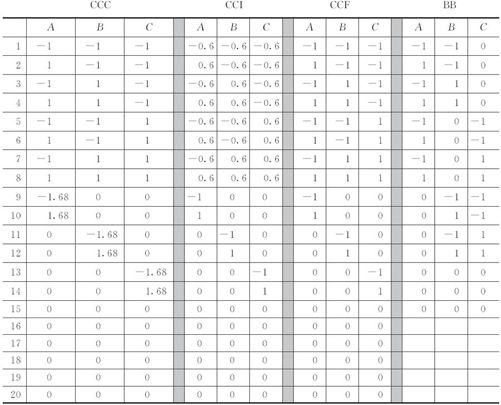
下面以3个因子为例，给出4种设计的计划表（见表13—27），其中前3种是CCD。第1种是普通的CCD（即CCC），第2种是CCI，第3种是CCF，第4种是Box-Behnken（BB）设计。前3种试验都要20次，Box-Behnken设计需要15次。这些设计都假定一开始就希望完成全部响应曲面设计，未作序贯设计的安排，而且表中所列数值假定已代码化。

表13—27　3因子4种响应曲面设计试验点计划表

13.5.2　响应曲面设计的计划

一旦识别出来的因子个数较少，就可以准备进行响应曲面分析方法。整个响应曲面设计的计划应该包含两个阶段：求最优试验区域；安排试验计划。

第一阶段要先求出最优试验区域。这阶段要先识别目前试验区域的状况，究竟此区域已经接近或达到了能使响应变量达到最佳值的最优区域了，还是仍然远离最优区域？我们以望大型（望小型完全相同）问题为例来讨论，望目型问题虽然可以通过多次重复试验方法然后再使用多响应曲面设计方法加以解决，但更常见的是使用本章13.6节介绍的参数稳健性设计方法。由于通常响应变量的极大值是在有曲面的弯曲的“山顶”部分达到的，因此，我们首先要特别认真地分析数据是否显示了弯曲性，或在数据拟合线性回归方程时的ANOVA表中是否显示了“失拟”现象。如果可以断言弯曲或失拟并不严重，则说明目前试验区域的位置仍然远离最优区域。就像爬山时，如果脚下虽然倾斜但仍然是较为平坦的区域，则说明此时仍然仅在半山坡上，离山顶依然遥远。这时，首要任务是先沿最陡峭的方向爬上去，当可以肯定达到山顶区域了，再建立细致的曲面方程来描述其数学规律。因此，我们可以归结响应曲面试验的两个阶段如下：

第一阶段：用最速上升法（steepest ascent search）寻找试验的最优区域。由于这时的回归方程是线性的，其等值线是些近似的平行直线，选取与等值线垂直的方向作为“最速前进方向”（path of steepest ascent），边沿此方向前进边做试验（对每个选定的位置只做一次即可）。若响应变量数值持续增加，则继续前进，直到响应变量数值出现了下降的情况才停止。选定刚才已得到的最佳值之处作为新一批响应曲面设计的中心点，转入下面的第二阶段。

第二阶段：在已确认为最优区域的范围内，进行响应曲面试验。要根据实际条件来安排CCD设计或Box-Behnken设计，在CCD型设计中又有CCC（中心复合序贯设计）、CCI（中心复合有界设计）和CCF（中心复合表面设计）三种选择可能。

下面先较详细地介绍第一阶段，即如何使用最速上升法来寻求试验的最优区域的问题。其基本思想可以用下列等值线示意图（见图13—52）显示出来。图中只讨论了2个自变量的情形，最优值是最大值（即问题是望大特性的），其实这种思路不难推广到更多维的情况。

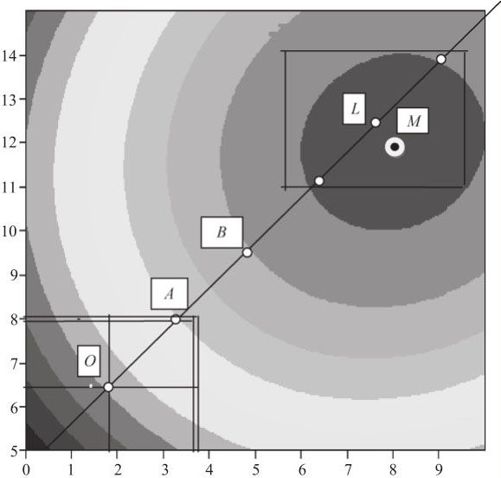
图13—52　最速上升法示意图

在图13—52中，整个区域是自变量所容许的范围，其中左下角的以O为中心的矩形区域是我们开始时进行因子试验的区域。容易看出，在分析响应变量的状况时，可以清楚地看出，在矩形区域内等值线的弯曲并不严重，响应变量与自变量间基本上还是线性关系。这时一方面可以用原来因子设计所使用的分析方法，另一方面说明这个区域离我们要寻求的整个区域上的最优值还很远。为了能尽快地找到最优值，应该沿着与等值线垂直的上升方向前进，这就是最速上升路径。当然前进时其步长不要太长，第一步常以刚好抵达因子试验的边界为最好（见图中点A），这时可以保证第一步迈出后其响应变量值肯定是增加的。沿此方向继续前进，且每前进一步都进行一次试验（如B等），获得其响应变量的值。如果此值继续增大，则沿此方向再前进一步，再获得其响应变量的值；如果此值已经开始减小（如图中抵达点L后，则再出发前进将使响应变量值减小），则在此方向上获得了响应变量的最大值点（即图中的点L）。当然一般点L不会正巧是响应曲面在整个范围内的最大值（例如本图中全部区域的真正最大值点位于点M），但我们可以得到一个以点L为中心的区域，再在此区域上安排若干试验点，尽量拟合一个二次曲面方程。由点A出发找到点B直到点L的上述方法常被称为“最速上升法”。通常可以认为这样做就能找到最优区域了。当然这不一定准确，如果仍未抵达最优区域，则重复上述最速上升方向前进的办法，甚至重复若干次，最后总是能找到最优区域的。

下面我们介绍最速上升法的一般计算原理，为方便起见，以下用两个自变量的情况作为代表来说明含义，而且假定是有望大特性的指标，朝响应变量增长的方向前进。

大家知道，如果等值线图中，各等值线基本上是平行直线（可能略有弯曲），则最速上升方向一定是与等值线垂直的方向。当弯曲很严重，或者根本没有“平行的趋势”，这主要是由于响应变量的回归方程中含有高次项或交叉项，这时，不存在固定的最速上升方向，想要尽快地寻求最大（小）值，只能在每个试验点上求此点处的最速上升方向，前进一步后对最速上升方向要另行计算。一般地，如果等值线方程为：

u＝F（x，y）＝C

则与等值线垂直的方向为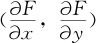。一般地，当维数为m时，其公式与此相同。

设等值线方程为：

则与等值线垂直的方向为：

在实际工作中常见的是线性方程，而且不含交叉乘积项，这样一来，我们就可以得到较简单的公式。一般地，若回归方程为下列形式：

则由（13—32）可知其等值线的垂直方向为：

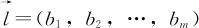
其单位向量（即长度为1的向量）为：

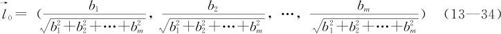
在实际问题中，前进的步长取长度为1并不总是合适的，太长了不一定能继续保持增长，太短了前进步伐太慢，一般认为最好的长度是前进一步后恰好抵达原来设计的边界。具体的寻求最速上升途径的过程，可以从更细致的图中看出。图13—53就是二维情况下寻求最大值的过程。图中，我们先在左下角以O为中心的矩形区域开始进行因子设计，获得的响应变量的等值线见该区域上的那组平行直线（假定没有失拟，弯曲也不严重），回归方程为u＝a＋b₁x₁＋b₂x₂，b₁和b₂是回归系数，在以b₁和b₂为两直角边的直角三角形中，斜边长度为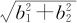，而斜边所指示方向就是最速上升方向（图中的OC方向）。在此方向上截取一段，使之恰好达到原来试验区域的边界点（图中的OA），则第一步前进到A，第二步沿此方向继续前进到B，以下依此类推，继续前进。这样求出最速上升方向不仅对两个自变量情况成立，一般到m个自变量依然成立。

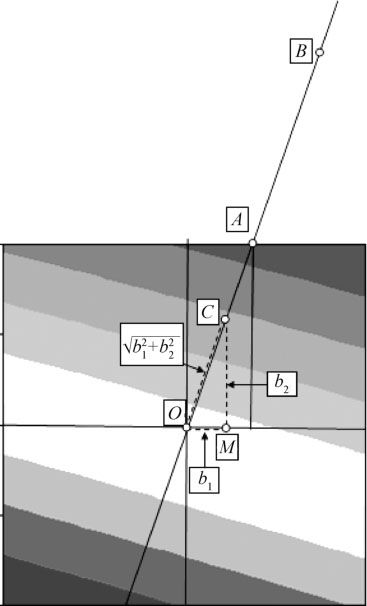
图13—53　最速上升方向计算示意图

需要注意的是，如果原来的自变量有范围的限制，一直沿最速上升途径前进并不一定是可行的，如果前进的途中已有某个自变量超出限制的情况，则应该令该自变量取相应边界上的值，其余自变量仍按原来的最速上升方向继续前进，直到响应变量的值出现下降为止。

在实际工作中，在求出A，B，…最速上升方向上的坐标点后，要分别进行一次试验以获得响应变量的值。如果响应变量的值是比前一个点上升的，则继续前进至下一个点；如果到某个点后，响应变量的值是比前一个点出现下降的，则证明在前一个点处已达到了此最速上升方向线上的最大值。再下一步应该是以这个最大点为中心，安排新一轮因子试验，这时如果弯曲不显著，证明离山的顶峰还差得远，则应重复上述寻求新的最速上升路径，以寻求新的最大点；如果弯曲严重，则应该以此次因子试验的结果为基础，安排更多点进行试验以形成一个响应曲面设计。求出响应变量的二次回归方程后，可以通过方程解出在试验区域内的最大值。这就是由因子设计逐渐发展至响应曲面设计的一般途径。

上述计算还是比较复杂的，而且还要对于原始自变量数据给出调整，因为要不断判断所选定的点是否超出允许的边界范围。为了计算方便，我们提供了宏指令，由回归方程直接求出最速上升方向，给出前进10步的相应各自变量的取值，这里的处理办法是：如果超界则以后皆取边界点的值。当然，通常前进用不了10步，一般就会发现响应变量出现下降的情况，这时就不要再继续前进了。如果真的到了前进10步仍然一直上升的话，那也应该在最后一点处安排一次因子试验，以重新拟合线性方程，因为前进多步后，回归方程常常会出现变化，以新的数据来计算新的最速上升路径将会更准确些。

需求最速上升方向并安排试验的方法称为“最速上升法”，这部分内容如我们刚才所介绍的，必须另行计算，因此一般都认为最速上升法本身并不属于响应曲面设计的内容。

下面我们举出实例，学会求出最速上升点坐标的方法，过程中还要学会调用宏指令的计算步骤。当然本宏指令仅限于交互作用项不显著时使用，如果交叉项显著，则要利用式（13—32）直接手算，这当然很麻烦，具体计算例题这里从略。

例13—16

焊接优化试验。经过因子试验，发现影响焊接拉拔力的因子有两个，且各自有其可行域：因子A为温度（450摄氏度至820摄氏度），因子B为点焊时间（50毫秒至160毫秒）。最后一次因子试验是这样进行的。因子A温度低水平取500摄氏度，高水平取560摄氏度；因子B点焊时间低水平取60毫秒，高水平取90毫秒。安排的是全因子试验加3个中心点，响应变量为拉拔力（单位：kg），其试验结果见数据文件：DOE_焊接（综）.MTW，数据见表13—28。

表13—28　焊接拉拔力试验结果数据表

试分析此次试验结果，并寻求最优点或最速上升方向，求出前进途径上前4个点的坐标。

解　这是一个全因子设计，其分析方法已在例13—4中作了详细介绍，这里不重复详细步骤，只是摘录出主要的计算结果。

回归方程为：

y＝141.2＋14.55Temp＋17.85Time

这里自变量皆为代码化数据，且交叉项不显著。残差诊断中虽然显示有些弯曲迹象，但统计分析显示并无显著弯曲。

其等值线图见图13—54。容易看出响应变量的最速上升方向，而且箭头的终点直达试验区域的边界。

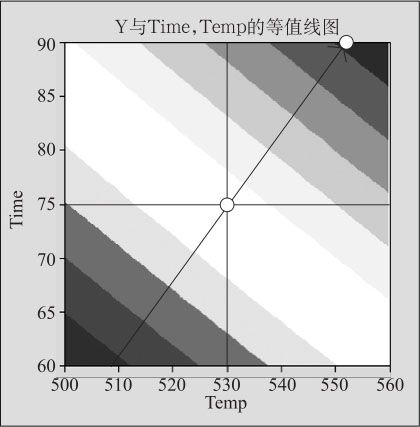
图13—54　焊接拉拔力试验结果等值线图

下面给出计算最速上升方向上各试验点的坐标的方法。

现在Temp的系数为14.55，Time的系数为17.85，长度为1的单位方向向量应该分别是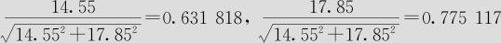。方向向量中第二项“Time”的系数最大，前进1/0.775117＝1.290128倍单位向量就达到此次因子试验的边界了，这时步长向量中的Time＝1.290128×0.775117×15＝15，Temp前进增量为1.290128×0.631818×30＝24.4538，这就是第一步的结果。用人工计算比较麻烦，可以使用宏指令，不但直接可以得到多步（这里限定10步）试验点的计算结果，而且一旦某个自变量达到该变量的试验区域外边界，则将保留其边界值而沿边界前进。调用宏指令方法如下。

打开数据文件DOE_POA.MTW，填写清楚有关信息（见表13—29的前6列）。

表13—29　求最速上升路径结果

这里第1列是回归变量名称（有几个自变量就填写几个，可以不止2个），第2列是回归方程中的系数，第3，4列填写本次试验时所取的因子高低水平值，第5，6列填写自变量所容许的最宽范围（如果无边界限制，则要填写随便选定的很小和很大的两个数，此2行不能空白）。以工作表文件DOE_POA.MTW为工作平台时，宏指令的调用非常简单，直接在“编辑＞命令行编辑器”中填写：

％doepoa

则计算机就可以把结果全部算出，包括中心点坐标、每步各自变量的增加值，以及从第1步、第2步，…，直到第10步，每次试验点的坐标N1，N2，…，N10。我们摘出前4点列入表13—29中的C9～C12。

在实际工作中，后续的步骤是这样的：按列出的试验点坐标进行试验，再对试验结果数据进行分析判断，决定最佳点位置。本例的计算结果状况类似于图13—52，这里从略，读者可自行补出。原来的因子试验预测已知中心点的响应变量值y值（即焊接拉拔力）为141.227，我们在N1处进行试验（近似取温度554摄氏度，时间为90毫秒），试验结果为171.5（按原来算出的回归方程计算出的预测值为171.304）。同样，在N2处（近似取温度579度，时间为105毫秒）试验结果为203.2；在N3处（近似取温度603摄氏度，时间为120毫秒）试验结果为238.6；在N4处（近似取温度627摄氏度，时间为135毫秒）试验结果为210.4。显然，N3处响应变量的值最大，沿最速上升路径再前进到N4，响应变量的值反而下降了。这就提示我们，现在可能已经到了弯曲显著的区域了，我们所能获得的最大值是在N3处出现的，下一步应该以N3为中心，再次安排因子试验。然后根据试验结果判断，究竟弯曲是否严重。如果弯曲不严重，则应再次按新拟合的回归方程求出新的最速上升路径，在此线上寻求更优值作为出发点；如果弯曲严重，则认为已经进入“最优区域”，应补充若干点，完成响应曲面设计，求出响应变量的二次回归方程，进而解出全区的最优点。

寻找试验的最优区域以后的步骤，主要是如何按响应曲面设计要求补充安排新试验点以及如何分析试验结果等，我们将在13.5.3节介绍。

下面介绍第二阶段，即进行响应曲面试验。这首先要创建响应曲面设计。

各计算机软件都能自动生成各种设计的表格，MINITAB软件操作的主要步骤是：

从“统计＞DOE＞响应曲面＞创建响应曲面设计（Stat＞DOE＞Response Surface＞Create Response Surface Design）”入口（见图13—55左上），首先在对话框中可以选定中心复合（CCD）或Box-Behnken设计，并选定因子个数。在“显示可用设计（Display Available Design）”框中可以看到不同要求下所需要的试验次数（见图13—55右上）。

在“设计（Design）”对话框中（见图13—55左下）选定总试验次数、中心点试验次数及α值。计算机提供默认的试验次数选择，这都是最佳选择，除非资源限制使试验次数实在达不到这些要求可以自行选择，否则通常不要改变试验次数。在α值的选取上有三种选择：（1）默认，这时计算机会按因子个数、旋转性还是正交性要求自动求出最佳的α值；（2）选“表面中心（α＝1）”，即安排CCF（中心复合表面设计）；（3）自定义α值。

在“因子（Factor）”对话框（见图13—55右下）中，除了要设定各因子的实际水平外，还要注意选取星号点的设置。当“水平定义（Levels Define）”栏中选定“立方体点（Cube Points）”时，表示这时设定的水平作为立方体点，也就是说这时选择的是CCC（中心复合序贯）设计，星号点将超出立方体。选定“轴点（Axial Points）”时，表示这时设定的水平作为轴上的星号点，即这时选择的是CCI（中心复合有界）设计，星号点将达到立方体边界而不超出，立方体点将向内收缩。

在“选项（Options）”对话框（界面图从略）中，若选定“随机化运行顺序”，则计算机会自动将运行顺序随机化；如果不选，就可以看到标准化的安排方法。在标准化顺序安排中，开始部分是因子设计点（立方体点），中间部分是星号点部分，最后是中心点，将来真正进行试验时，再将试验顺序随机化也行。这些与其他试验设计相同，不再赘述。

例13—17

提高密封胶条黏合力试验。影响黏合力的3个因子是：A：烘烤温度（220～240摄氏度），B：烘烤时间（6～10秒），C：黏合压力（100～140帕）。在因子设计时，分别取下列条件，安排了全因子试验（2³＋3）：

因子A：烘烤温度，低水平220，高水平240（摄氏度）

因子B：烘烤时间，低水平7，高水平9（秒）

因子C：黏合压力，低水平110，高水平130（帕）

试验后发现，数据呈现明显弯曲状况，希望进一步安排些实验以拟合响应曲面方程。

由于要进行序贯试验，最好选CCD型设计。从“统计＞DOE＞响应曲面＞创建响应曲面设计（Stat＞DOE＞Response Surface＞Create Response Surface Design）”入口（见图13—55），在对话框中选定中心复合设计，并选定因子个数为“3”。在“显示可用设计（Display Available Design）”框中可以看到未划分区组时试验次数为“20”（见图13—55右上）。

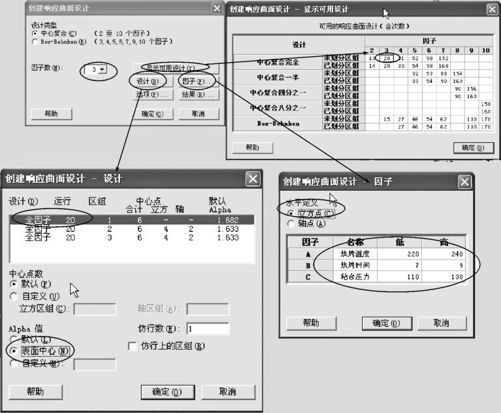
图13—55　响应曲面设计操作图

打开“设计（Design）”后，本例中试验需要20次，这是可行的，不必修改；中心点数也不用另设。但选哪种CCD，则要考虑更多条件。由于在烘烤温度上，原来的试验温度条件已经取在边界上了，不允许再超界因而不能使用CCC，而为了保持序贯性，只能放弃有旋转性的CCI，故而应选用CCF，即在“设计（Design）”中选定“表面中心（Surface Center）”。

打开“因子（Factors）”后，要选“立方点（Cube Point）”，再填写各因子名称及水平。

打开“选项（Options）”后，为了看清结构，暂时先删除“随机化（Randomize）”，得到下列结果（见表13—30）：

表13—30　3因子响应曲面CCF设计表

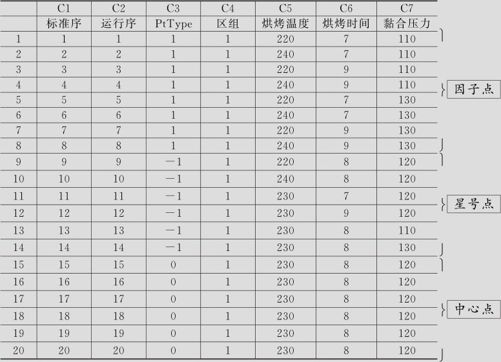
在表中的20次试验中，第1至第8号因子点以及第15至17号中心点（共11个点），已经在因子设计阶段获得了数据，只要将这些结果填在后面第8列上，然后再补充其他9个试验，就可以完成全部响应曲面的试验任务。

13.5.3　响应曲面设计的分析及实例

响应曲面设计也是试验设计的一种，其分析方法当然应该与一般的试验设计的分析步骤相同，其流程图如图13—14所述，也分为五大步骤。

响应曲面试验的分析方法与一般的试验设计分析的差别就在于其选项。响应曲面试验设计要拟合的是二次曲面，其一般模型是（以两个自变量为例）：

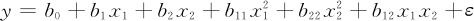
选项比过去增加了各自变量的平方项。另外，在计算机的输出中，输出的表达上也有些细微的差别，在此不多加叙述，详细比较可以从下面例题中看出。

例13—18

提高烧碱纯度问题。在烧碱生产中，经过因子的筛选，最后得知反应炉内压力及温度是两个关键因子。在改进阶段先进行了全因子试验，因子A压力的低水平及高水平取为50帕及60帕，因子B反应温度的低水平及高水平取为260摄氏度及320摄氏度。在中心点处也作了3次试验，试验结果如表13—31所示（数据文件：DOE_烧碱纯度（响应1）.MTW）。

表13—31　烧碱纯度的全因子设计数据表

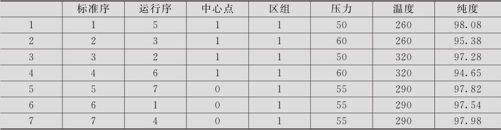
对于这批数据按全因子试验进行分析，其结果如下：

第一步：拟合选定模型。

首先将全部备选项列入模型，这里包含A压力，B温度，及它们的交互作用项AB（压力*温度），得出结果如下：

拟合因子：纯度与压力，温度

纯度的效应和系数的估计（已编码单位）

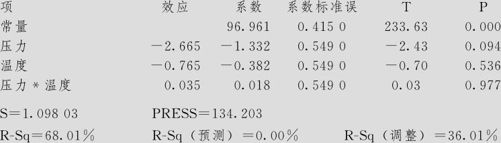
纯度的方差分析（已编码单位）

从ANOVA表首先可以看到，模型的总效果（主效应及2因子交互效应项）不显著。另外可以清楚地看到，在弯曲一栏中，p值只有0.014，显示这里响应变量纯度有明显的弯曲趋势。另外，在残差分析中，由残差对各自变量的图（见图13—56）中也验证了严重弯曲的存在。

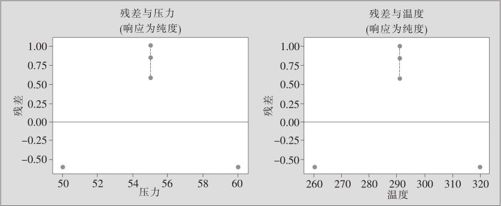
图13—56　纯度残差对自变量“压力”及“温度”的散点图

这些结果说明：在本问题中，试验数据有明显的弯曲，这也提示我们，现在进行的试验区域可能已达到响应变量的最佳区域了。这时对响应变量纯度单纯拟合一阶线性方程不够了，要再补充些“星号点”，构成一个完整的响应曲面设计，拟合一个含二阶项的方程就可能解决问题。我们补做4次星号点上的试验，而且由于我们确信这批新做的试验，其各方面条件都与上批相同，因此直接将它们并在一起进行分析。如果没有这种假定，两批试验应该当作两个“区组”来对待才能使分析更准确。补充的4个“星号点”试验结果见表13—32（全部数据形成的文件：DOE_烧碱纯度（响应2）.MTW）。

表13—32　烧碱纯度优化问题第二批试验数据表

对全部11个点构成的CCC（中心组合序贯）设计进行分析，拟合一个完整的响应曲面模型。分析结果如下：

第一步：拟合选定模型

从“统计＞DOE＞响应曲面＞分析响应曲面设计（Stat＞DOE＞Response Surface＞Analyze Response Surface Design）”窗口进入（见图13—57），点击窗口“项（Terms）”后，界面如图13—57右上半部分所示。

图13—57　响应曲面设计的分析操作图

首先将全部备选项列入模型。这里包含A（压力），B（温度），及它们的平方项AA，BB以及它们的交互作用项AB。获得的计算结果如下：

结果：DOE_烧碱纯率（响应2）.MTW

响应曲面回归：纯度与压力，温度

分析是使用已编码单位进行的。

纯度的估计回归系数

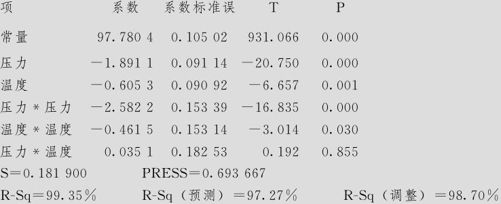
纯度的方差分析

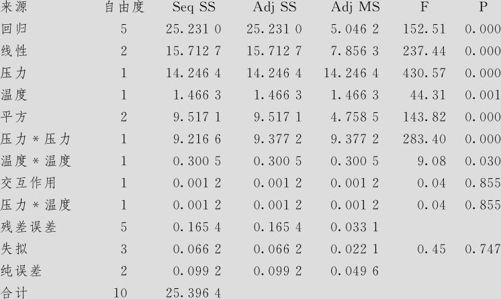
在第一步要注意观察下面几处要点：

（1）看ANOVA表中的总效果。在本例中，对应回归项（Regression）的p值为0.000（即＜0.001），表明应拒绝原假设，即可以判定本模型总的说来是有效的。

看ANOVA表中的失拟现象（Lack of Fit）。在本例中，失拟项的p值为0.747，其数值远比临界值0.05大，表明无法拒绝原假设，即可以判定本模型并没有失拟现象。

（2）看拟合的总效果多元全相关系数R²（即R-Sq）及修正的多元全相关系数（即R-Sq（调整））。本例中，R-Sq为99.35％，R-Sq（调整）为98.70％，二者已经很接近了，但如果将影响不显著的效应删去，二者会更接近。

S值的分析。本例中，S＝0.1819。

R-Sq（预测）＝97.27％，PRESS＝0.693667。

（3）各项效应的显著性。在计算结果的最开始参数估计中，列出了各项效应及检验结果。可以看出，压力、温度，及它们的平方项压力压力、温度温度都是高度显著的，而它们的交互作用项压力*温度则不显著（p值为0.855），将来修改模型时，应该将此交互作用项删除。总的来说，模型拟合效果是好的。

第二步，进行残差诊断

利用计算机自动输出的残差图（见图13—58和图13—59）可以很容易地进行残差诊断。四合一残差诊断包括4项诊断（见图13—58）。

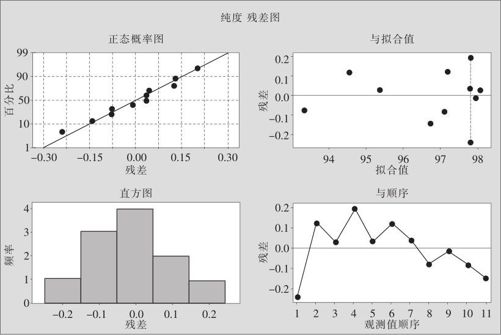
图13—58　响应曲面设计的四合一残差分析图

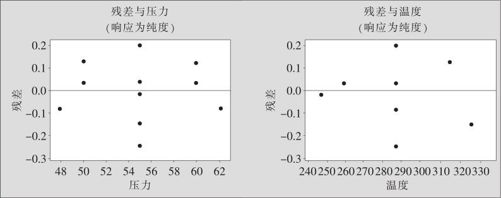
图13—59　残差对于自变量的散点图

从6张图中可以看出，残差的状况是正常的。我们解释一下，如何分析图13—58右上图是否有残差不齐性的问题，粗略看来好像有“喇叭口”的趋势，但在图中先要找到3个中心点的位置。由于3个中心点的拟合值一定相同，所以3个中心点在右上图中一定会出现3点竖直排列的状况（如图中虚线所示），这完全是试验误差形成的波动，如果别的点的残差没有超过这些中心点残差波动的范围，就应该视为正常，此图无问题。

第三步：判断模型是否要改进

从残差诊断中看出，模型基本上是好的，没发现残差对自变量的“S”形或“反S”形弯曲，因此不需要增加x的高阶项。为了确认残差对于预测值是否没有非齐性，是否要对y进行变换，还可以使用宏指令来定量地分析（参见13.3.3.2节）。

调用宏指令，格式如下：

％boxcoxdoe　C7　M1　6　C21-C60

计算结果见图13—60。

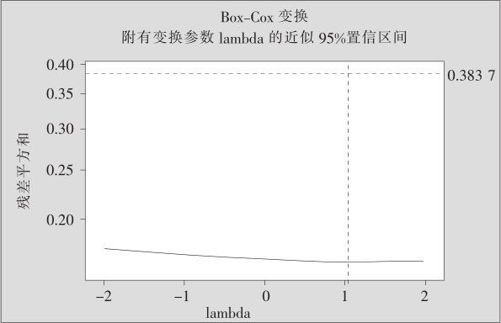
图13—60　响应曲面设计的Box-Cox变换分析图

在λ＝1处，残差平方和曲线落在95％置信曲线下方，因此说明此例中对于y不需要进行变换。

只是在检验各项效应中，发现2个自变量间的交互效应项不显著，因而改进模型主要是删除此不显著项。因此，实际上，又要返回第一步。

新第一步：拟合选定模型

本例中，在重新拟合模型的计算时要删去交互作用项“压力*温度”，保留其他项，再次计算所得的结果如下：

响应曲面回归：纯度与压力，温度

分析是使用已编码单位进行的

纯度的估计回归系数

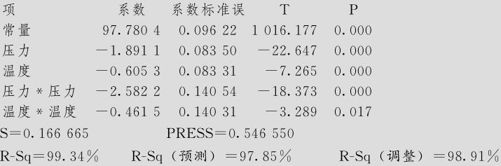
纯度的方差分析

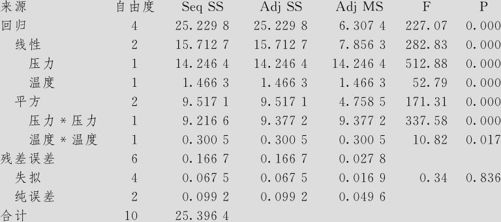
纯度的估计回归系数，使用未编码单位的数据

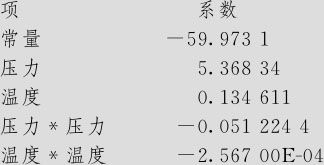
对于这次的计算结果，我们仍用前面介绍过的方法与步骤进行分析。此时观察到下面几处要点：

（1）先看ANOVA表中的总效果。在本例中，对应回归项（Regression）的p值为0.000（即＜0.001），表明应拒绝原假设，即可以判定，本模型总的说来是有效的；看ANOVA表中的失拟现象，在本例中，对应失拟项的p值为0.836，其值远比临界值0.05大很多，表明无法拒绝原假设，即可以判定，本模型删去了一项，但并没有造成失拟现象。

（2）看删减后的模型是否比原来有所改进。我们把两个模型计算的多元全相关系数R-Sq和修正的多元全相关系数R-Sq（调整），标准差的估计量S，预测残差平方和（PRESS）及R-Sq（预测）各项值汇总成表13—33。

表13—33　全模型与删减模型效果比较表

可以看出，由于模型项数减少了一项，R-Sq通常会有微小的降低，但关键是看R-Sq（调整）是否有所提高（本例R-Sq（调整）是有提高的），S的值是否有所降低（本例S的值由0.1819降为0.1667），预测残差平方和（PRESS）是否有所降低（本例由0.693667降为0.54655），R-Sq（预测）是否有提高（本例由97.27％提高到97.85％）。本例结果证明删除了不显著的交互作用项后，回归的效果更好了。

除上述常用结果外，为了获得更精密的数值结果，还可以输出更精确的对于原始数据的回归系数值。

由上述数值，可以写出最后确定了的回归方程：

新第二步：进行残差诊断

没有发现任何不正常情况（详细结果从略），可以确认上述模型为我们最终选定的模型，不用再进行第三步修改模型了。

第四步，对选定模型进行分析解释

本问题是希望纯度越大越好，这里两个平方项系数皆为负，又没有交叉项，可以肯定将可以从回归方程中（令两个偏导数为0）求得最大值（但不能保证此最大值一定落在原来试验范围内）。在求解前，我们先看一下等值线图及曲面图（见图13—61）。从图中可以清楚地看到，在原试验范围内确实有个最大值。

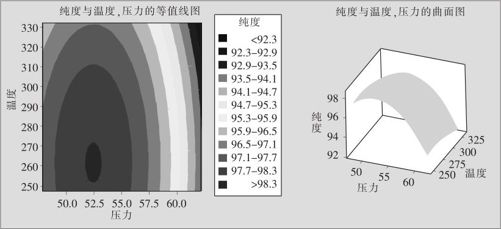
图13—61　响应变量的等值线及曲面图

利用人工解方程的方法，由于两因子交叉项为0，可以对两个变量分别求解最大值。由一元二次函数性质知，y＝ax²＋bx＋c，当a＜0时，y的最大值将位于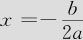处，因此也可以得到最优解。当

压力＝5.36834/（2×0.0512244）＝52.4（帕）

温度＝0.134611/（2×0.0002567）＝262.2（摄氏度）

时，所获得的纯度最高。

计算机也提供了响应优化器，可直接获得最优解。从“统计＞DOE＞响应曲面＞响应优化器（Stat＞DOE＞Response Surface＞Response Surface Optimizer）”入口，选定“响应（Response）”为“纯度”，在“设置”中，选定“目标”是“望大”，“下限”填写为“80”，“望目”填写为“100”，则可以得到图13—62，这里为计算方便，对自变量只保留了一位小数。结果与我们手算结果相同，纯度将达到98.325。这个结果比我们已经做过的试验中最好的结果（98.08）还要好些。

图13—62　响应变量优化器的计算结果图

为了获得置信区间，从“统计＞DOE＞响应曲面＞分析响应曲面设计（Stat＞DOE＞Response Surface＞Analyze Response Surface Design）”入口，选定“响应（Response）”为“纯度”，在“预测（Prediction）”中，在自变量设置处，填写“52.4，262.2”，则可以得到下列结果：

根据该模型在新设计点处对纯度的预测响应

前一个置信区间（95.0％ CI）表明的是回归方程上的点的置信区间，此值可以作为改进的结果的预报写在总结报告中。后一个置信区间（95.0％ PI）表明的是以上述回归方程上的预测值的置信区间为基础，加上观测值固有的波动所给出的置信区间，这就是将来做一次验证试验时将要落入的范围，可供做验证试验时使用。如果要求出多次（例如3次）验证试验的平均值，就要使用宏指令，这里有件事情要注意，那就是要确认自己所存储的设计矩阵究竟是已编码数据还是未编码（即原始）数据。如果在进行分析时使用的是代码数据，存储的设计矩阵也是编码后的数据，最优设置之值也应该是已编码的数据；如果求最优设置时对自变量常使用的是原始数据，则要对原始数据的设计矩阵再存一次才能使用。设M1，M2分别是全模型（6个自变量）及删减模型（5个自变量）的编码数据设计矩阵，M3是原始数据5个自变量的设计矩阵，则调用宏指令应该是：

％ypred　C7　M3　5　3　C8

得到最终结果为：

m次验证试验均值的95％置信区间

m＝3.0

模型的均方误（MSE）＝0.027777

95％置信区间下界＝98.0094

95％置信区间上界＝98.6407

13.5.4　多响应曲面设计的最优分析

前面各节讨论响应曲面分析仅限于单个响应变量的问题。实际工作中常遇到要同时考虑多个响应变量的情况，例如希望断裂强度越大越好，同时希望厚度越小越好；希望质量水平越高越好，但同时希望成本越低越好，等等。如何同时考虑多项指标是个很复杂的课题。这里有两种思路：一种是设法将多个指标用某种方式结合成某个综合的单指标，仍将问题化为单指标来考虑；另一种思路则是设法直接处理多指标问题。本节将只讨论后种思路。下面通过一个例题阐明解决这类问题的具体方法，结合MINITAB软件提供的两个窗口来具体实现最优化。我们先讨论一个实际问题。

例13—19

验血校正试验。本问题是要求同时考虑4项响应指标：

（1）吸收（absorb），要求：≤61.85，希望越小越好；

（2）模糊（blanking），要求：≥300；

（3）比率（ratio），要求：介于0.4～0.5之间；

（4）分离（separation），要求：≥200。

影响这几项指标的自变量有2个：

A：抗体（antibody），取值要在（10，40）之内；

B：试剂（reagent），取值要在（20，50）之内。

由于自变量范围明确不能超越，因此安排了CCI（中心复合有界）设计，试验费用昂贵，中心点只安排了2次，试验结果如下（见表13—34）（数据文件：DOE_验血（多响应）.MTW）。

表13—34　验血校正试验数据表

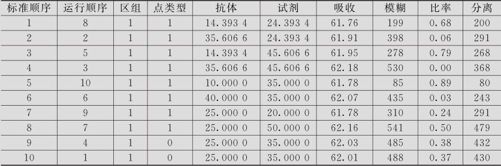
希望能找到满足所有要求条件且吸收越小越好的最佳因子设置。

先对这4个响应变量分别进行响应曲面设计分析，观察对于各响应变量有显著影响的自变量项（当然它们不全相同），取这些变量的全部：A，B，AA，BB，AB。

多响应变量的优化有两个工具可以使用：重叠等值线图及响应优化器。

重叠等值线图（Overlaid Counter Plot）就是对于选定的自变量区域内，将多个响应变量的取值等值线画在同一张图内，这便于观察同时满足多项要求的状况。从“统计＞DOE＞响应曲面＞重叠等值线图（Stat＞DOE＞Response Surface＞Overlaid Counter Plot）”入口（界面见图13—63左），选定“响应（Response）”为全部4个响应变量；打开“等值线（Counter）”窗口（界面见图13—63右），在各响应变量设置处，填写各自范围。对于只有“≤”者，将其上界值写入“高”，将自己任意选的低值写入“低”；对于只有“≥”者，将其下界值写入“低”，将自己任意选的高值写入“高”；对于同时有“≤”及“≥”者，将其下界值写入“低”，将其上界值写入“高”。这样就可以得到下列重叠等值线图结果（见图13—64）。

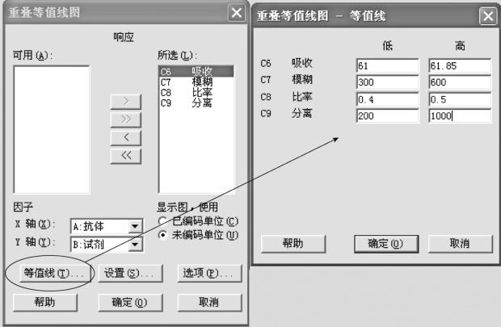
图13—63　多响应变量重叠等值线图操作

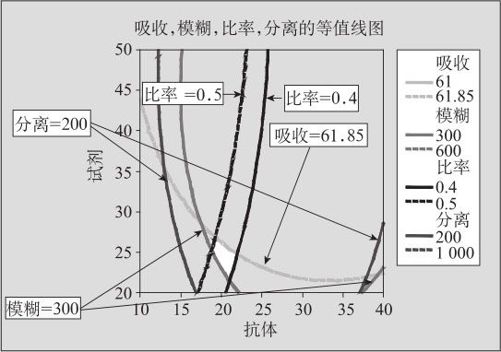
图13—64　多响应变量重叠等值线图

在重叠等值线图中，所有带阴影色的区域都是“不可行区域”，中间左下方有个白色“可行域”。如果输入“响应（Response）”时，逐个填写响应变量，则在打开“等值线（Counter）”窗口（界面见图13—63右）后，逐个填写各自范围，则可以看到等值线的个数逐渐增多，填充导致可行域逐渐缩小的过程。

为了寻求最优设置，我们可以用工具“十字线”协助。对准图形点鼠标右键，找到“十字线”；或从工具栏中点击“十字线”，即可以产生能自由移动的十字线（见图13—65）。在移动十字线时，计算机在左上角自动跳出“坐标窗”显示十字线位置及各响应变量的数值。从本例来看，希望吸收越小越好，则应该让“比率”尽可能接近下限0.4，让“模糊”也尽可能接近下限300，即应当将十字线尽可能靠近此二线的交点处（菱形的最下角）。这样，“吸收”就尽可能地小了，可以达到61.789。

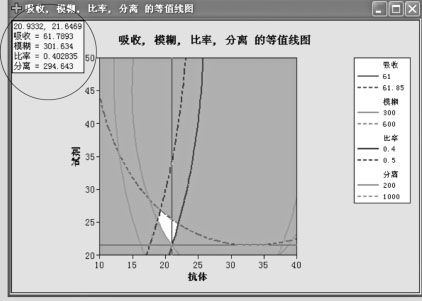
图13—65　多响应变量重叠等值线中的十字线

多响应变量的优化还有另一个工具可以使用：响应优化器（Response Optimizer）。

响应优化器可以同时处理多个响应变量的优化设置选择问题。从“统计＞DOE＞响应曲面＞响应优化器（Stat＞DOE＞Response Surface＞Response Optimizer）”入口（界面见图13—66左上），选定“响应（Response）”为全部4个响应变量；打开“设置（Setup）”窗口（界面见图13—66右上），在各响应变量设置处，填写各自优化目标。对于只有“≤”者，将其目标写为“望小”，上界值写入“上限”，将自己任意选的低值写入“望目”，“下限”空白；对于只有“≥”者，将其目标写为“望大”，下界值写入“下限”，将自己任意选的高值写入“望目”，“上限”空白。由于多个响应变量选优问题可能很复杂，计算机要先找到“初始值”作为出发点，如果搜索几次都不能满足所设要求时，计算机会“自动罢工”而无任何有意义成果输出。为此，我们要打开“选项（Options）”，输入一个“可行点”（不一定很准确），然后计算机就可以开始正常的“选优”计算了。在本例中，我们将因子A（抗体）设为21，将因子B（试剂）设为21.5，就可以计算了。

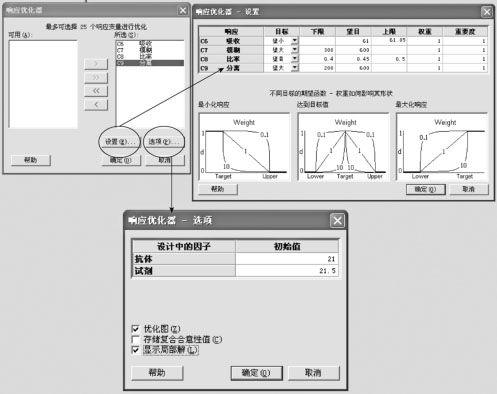
图13—66　多响应变量响应优化器操作

计算后，可以得到下列响应最优化结果，见图13—67。

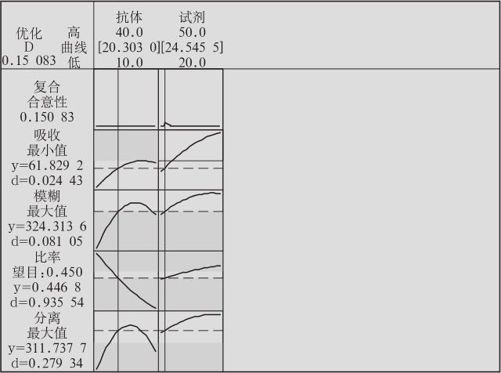
图13—67　多响应变量响应优化结果

但是，上述结果很显然是并不令人满意的。如果调整“重要性”，将“吸收”的“重要性”提高到10，其余三项的“重要性”降为0.1，则结果能达到比重叠等值线更好（其实是更精确）的结果（见图13—68）。设置为：因子A（抗体）设为20.9903，因子B（试剂）设为21.5152，吸收可以降低到61.7877。

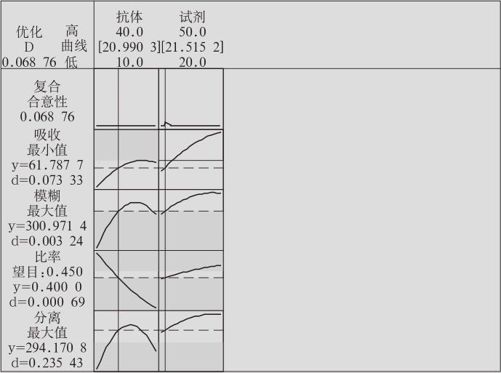
图13—68　多响应变量响应优化结果

我们前面已经说过，在处理多响应变量的优化问题时，有两个工具可以使用：重叠等值线图及响应优化器。从这个例子可以看出应用重叠等值线图显得直观、方便，但实际上，每张等值线图只是针对两个自变量时绘制的，多个自变量时必须要同时考虑多张重叠等值线图，这样一来，重叠等值线图实际上只在仅有两个自变量时才特别有效，变量一多，应用很不方便。下面我们就举例说明这种多自变量的情况，同时，此例也是对于解决望目特性问题的介绍。

例13—20

黏接膏体黏接力试验。不干胶黏接广泛应用于实际工作中。有时，对于黏接膏体之黏接力并非希望一定最大，而是希望与某个理想值最接近（有一定的黏度又容易撕开，且不同的被包装物及不同的使用条件对理想值的要求也不相同）。本问题是要求黏接力达到一个理想值，同时希望黏接力的波动最小。

影响本黏接膏体之黏接力的因子有三个。因子A为酚醛树脂％含量；因子B为甲醛硝钠％含量；因子C是反应温度。响应变量为黏接力，按每个搭配条件重复进行3次试验。试验是在最优区域内的CCI试验，因子A（酚醛树脂％含量）取值为32％～36％；因子B（甲醛消钠％含量）取值为1.6％～1.8％；因子C是反应温度（120摄氏度～160摄氏度）。由于自变量范围明确不能超越，因此安排了CCI（中心复合有界）设计，按Box响应曲面设计经典设计，中心点安排了6次，试验结果如下（见表13—35，数据文件：DOE_黏合剂（多响应）.MTW）。

表13—35　黏合剂试验数据表

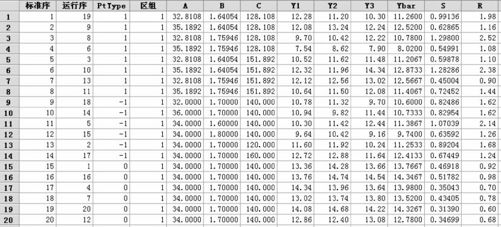
希望能找到在平均黏合力为13.5（千克）时，波动最小的最佳因子设置。

解　先求出3次试验结果的均值Ybar和标准差S对于Ybar和S分别进行响应曲面设计的分析，发现这两个响应变量所含各个因子、它们的平方项、交互作用项几乎都是显著的（只有Ybar中的AC项不显著）。先对Ybar的取值状况进行分析，绘制其等值线图，发现在设计区域内在设计的中心点附近确实可以有最大值。其等值线图见图13—69。

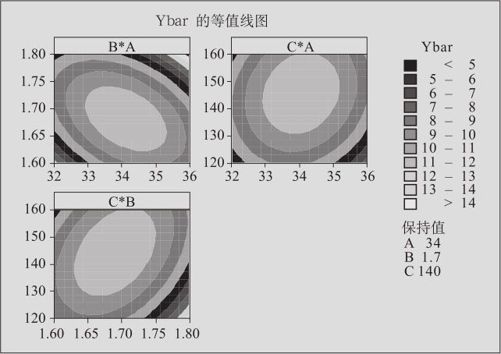
图13—69　黏合剂试验的多响应变量等值线图

由于自变量有3个，分三组，每次只讨论两个自变量，如果要求得出最优值（特别是同时求出两个响应变量的最优值）是很麻烦的事，因为确实很难同时看到未选入的那个自变量变化后的状况。我们改为直接使用响应曲面的优化器，操作如图13—70所示。

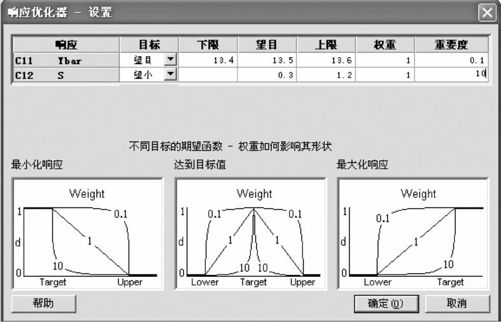
图13—70　黏合剂试验的优化器使用图

其计算结果见图13—71。

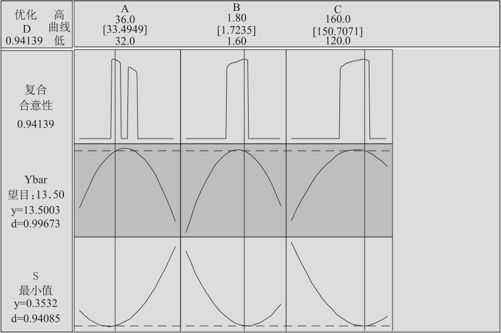
图13—71　黏合剂试验的优化结果图

对于望目特性的响应变量选优的问题，可以将望目值设为目标，然后指定某种精度就可以计算了。我们先取的是Ybar的限制为（13.4，13.6）。这时我们得到，在A＝33.4949，B＝1.7235，C＝150.707时，Ybar可以达到13.5003，S可以小至0.3532。但我们不要满足于这个结果。如果我们在使用响应曲面的优化器时，将图13—70中响应变量的取值要求稍加改动，将Ybar的限制由（13.4，13.6）改为（13.49，13.51），则Ybar可以达到13.5026，S可以更小至0.3527，这比上述结果更好。如此说来，是否对于望目特性的响应变量都可以用缩小其允许范围而得到改进呢？显然不是，如果我们在使用响应曲面的优化器时，将Ybar的限制由（13.49，13.51）改为（13.499，13.501），则Ybar表面上有些改变，但S却变大了：这时Ybar为13.5000，S却变大为0.5134。这说明，如果对望目特性要求得过严，则满足此条件的自变量范围将更窄，一般说来S常常会变差的。

下面我们对于多响应变量优化器使用中的“重要度”加些补充说明。

仍以黏接力设计为例，有时我们希望获得黏接力最大，同时希望黏接力的波动达到最小，这时如何选择“最优值”呢？

首先我们先对响应变量Ybar求最大值。这时按单响应变量优化处理，暂不考虑标准差S的问题。容易知道，Ybar的最大值为13.9302，这是在A＝34.1010，B＝ 1.6889，C＝144.6465时得到的。如果对响应变量S求最小值。这时仍按单响应变量优化处理，暂不考虑Ybar的问题。容易知道，S的最小值为0.3192，这是在A＝ 32.4444，B＝1.7313，C＝160.0时得到的。如果同时考虑Ybar达到最大值及S达到最小的问题，则可以肯定的是，两者所能达到的最优值都一定不如只考虑单响应变量时的好。这时必须考虑到二者的重要性设置，对于不同的设置肯定会得到不同的结果。当二者的重要度相等时（二者皆取1，这与同样取别的值结果是相同的），可以看到，Ybar的最大值为13.7905，S的最小值为0.3783，这是在A＝33.7778，B＝1.7111，C＝145.859时得到的。当二者的重要度发生变化时（在MINITAB中，重要度的取值限定在0.1～10），则最优值会发生变化。例如，当Ybar的重要度取10，S的重要度取0.1，这时Ybar的最大值为13.9299（从图13—69中可以看出，本例的响应曲面顶部曲率很小，几乎是个“平顶山”，这时也差不多达到了单响应变量时达到的最大值13.9302），S的最小值为0.4414（远高于单响应变量时的最小值0.3192），这是在A＝34.1010，B＝1.6889，C＝144.242时得到的；当Ybar的重要度取0.1，S的重要度取10，这时Ybar的最大值为13.0685，S的最小值为0.3390，这是在A＝33.1313，B＝1.7273，C＝153.131时得到的。

总之，当自变量个数超过2时，等值线图的应用受到诸多限制，响应变量优化器则显示出很大的威力，按不同的要求可以得到不同标准下的“最优点”。