我的书签
添加书签
移除书签第四章 放射性向本来无放射性的物质传播
在研究放射性物质的过程中，皮埃尔·居里和我都观察到过一种奇特的现象，那就是，凡是靠近镭盐放置的物品，经过一段时间，也都会变得具有放射性。在我们发表的关于这个现象的第一篇论文中，我们已经着重指出，原来没有放射性的物质以这种方式获得了放射性并不是由于有外来的放射性粒子附着在这些物质的表面。这里，我将从两个方面来进一步证明，这个结论是毋庸置疑的。不仅我在下面介绍的这些实验全都支持这种看法，而且，本来无放射性的物质被激发出来的放射性在停止镭的影响之后逐渐消失所遵循的那些规律，也能够说明这一点。
我们将新发现的这种现象命名为：感生放射性。
在第一篇关于这个现象论文中，我们列出了感生放射性的几个基本特征。我们选择了由不同物质制成的隔板，先把它们放在固体镭盐的近旁，激发出放射性。然后，再用电学法研究这些隔板的放射性。我们观察到下面这些事实：
1．暴露在镭射线作用下的隔板，获得的放射性随暴露时间而增加，并按照渐近规律达到一个确定的极限。
2．已经被镭的作用激发出放射性的隔板，在脱离镭的作用以后，它的放射性会在几天之后消失。而且，它获得的这种感生放射性随时间而减弱，也是按照渐近规律趋于零。
3．在其他条件都相同时，不同的隔板被相同的镭试样感应得到的放射性与隔板材料无关，玻璃、纸和金属，全都获得了同等程度的放射性。
4．同一个隔板被不同的镭试样感应得到的放射性有不同的极限值，镭试样的放射性越强，这个极限值越高。
此后不久，卢瑟福发表了他的研究结果，指出钍的化合物也能够产生感生放射性现象。他的发现，除了上面提到的这些规律，还增加了一个新的重要事实：带负电的物体获得的感生放射性要大于其他物体获得的感生放射性。卢瑟福还观察到，从氧化钍侧旁流过的空气在大约10分钟内仍然还保持有明显的电导性。处在这种状态的空气能够把感生放射性带给没有放射性的物质，特别是那些带负电的物质。卢瑟福对他发现的这些事实给出了一种解释。他认为，钍的化合物，特别是钍的氧化物，在向外散发一种放射性射气 。这种射气能够被气流带走，而且带正电。这种射气就是感生放射性的来源。多恩改用含有镭的钡盐重复了卢瑟福使用氧化钍所做的那些实验。
德比尔纳在他的实验中则发现，锕也能够使它近处的物体出现明显的感生放射性。同钍的情形一样，使用锕，气流传播放射性的作用也非常明显。
感生放射性现象的具体表现各种各样，在敞开环境的空气中由镭激发近处物质所感应的放射性，测量结果简直毫无规律。但是皮埃尔·居里和德比尔纳发现，如果在密闭容器内进行实验操作，这种现象还是很有规律的。于是，他们便改在密闭的空间内来研究感生放射性。
在密闭空间内感应的放射性
皮埃尔·居里和德比尔纳所进行的实验是把放射性物质装入一个开有小孔o 的小玻璃瓶a 内（图11），再把玻璃瓶放在一个被罩起来的密闭空间的中心。在这个密闭空间内放入几块用不同材料制成的测试板A、B、C、D、E。这些测试板被放射性物质照射一天之后都获得了放射性。不论测试板是用什么材料制成（铅、铜、铝、玻璃、硬橡皮、蜡、纸板、石蜡），只要尺寸相同，测试板所获得的放射性强度都相同。但是，每一块测试板任何一面获得的放射性，与在敞开空气中进行实验时该测试板同一面获得的放射性比较起来，各自的强度都更大。
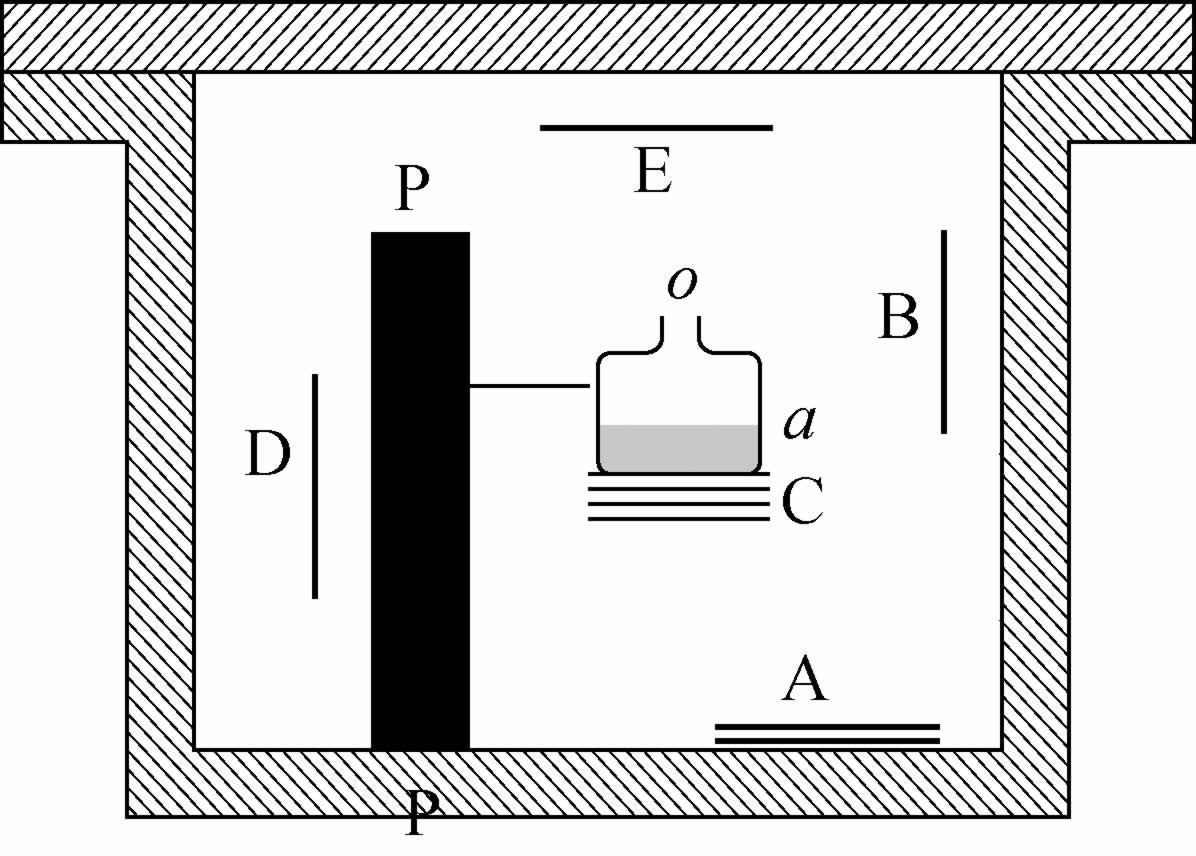
图11
把玻璃瓶a 完全密封起来重复上述的实验，则没有产生感生放射性。
由此可见，感生放射性并不是由镭的辐射直接产生的。正因为如此，所以在上述实验中，测试板D虽然被一层厚铅板PP与放射性镭隔开，它也同B和E一样感应了放射性。
事实上，放射性是由空气从放射性物体一点一点地运送到那最后被激发出感生放射性的物体上的。即使只有一根非常细的毛细管，空气也能从其中通过把放射性运送到很远的距离。
同固体镭盐相比，它的水溶液引起的感生放射性更强，而且也更有规律。
液体也能够获得感生放射性。例如，把纯水和镭盐溶液一起放入一个密闭空间，纯水就被赋予了放射性。
有一些物质（磷光和荧光物质、玻璃、纸、棉花、水、各种盐溶液），把它们放入具有放射性的密闭空间，还能发出亮光。在这种环境，具有磷光特性的硫酸锌会显得特别光辉夺目。然而，这些发光物质获得的感生放射性，与在相同条件下被激发却不发光的金属或者其他物质获得的放射性，是一样的。
在密闭容器内被激发而获得放射性的任何物质，不论是什么材料，它们的放射性都会随时间增加而达到一个极限值 。而且，对于同样的材料和在同样的实验条件下，这个极限值总是一样的。
感生放射性的极限与放射性密闭空间中气体（空气、氢气、二氧化碳）的种类和压强无关。
在同一个密闭空间激发的感生放射性的极限取决于放射性溶液中含镭量的多少，似乎与镭的数量成正比。
气体在感生放射性现象中所起的作用
射气 在放置有固体镭盐或者镭盐溶液的密闭空间，充满其中的气体也具有放射性。用管子抽出其中的气体把它们收集在试管中，这些气体仍然保持有放射性。这时，试管壁也获得了放射性，试管内的气体则会在黑暗中发出亮光。这种放射性和发光性最终会完全消失。但是，这种消失是一个渐进过程，一个月后还有可能探测到放射性。
自从我们开始研究放射性以来，皮埃尔·居里和我就经常会在加热沥青铀矿时提取到一种放射性很强的气体。但是，正如刚才提到的实验，这种气体的放射性最终会完全消失。
我们没有在这种气体的光谱中看到新的谱线，由此判断它不可能是一种具有放射性的未知气体。我们后来才知道，原来那就是感生放射性现象。
由此可见，钍、镭和锕这几种放射性物质感应出放射性，全都是借助气体逐渐传播实现的。放射性被气体从放射性物质慢慢传播到密闭容器的四壁；如果从其中抽出气体，那种能够激发出放射性的源物质便随气体跑到了容器外面。
在用电学法借助图1所示的装置测量镭化合物的放射性时，电容器两块极板之间的空气本身也带有放射性。不过，当极板之间有气流通过时，并没有察觉到电流强度有所下降。这说明，分布在极板之间空间的那种放射性同固体状态的镭试样的放射性比较起来，可以忽略不计。
但是，若用放射性钍进行实验，就不能不考虑电容器极板之间空气的放射性的影响。我在测量钍化合物的放射性时，测得的电流作无规律变化，那就是由于我使用的电容器是暴露在敞开空气中的缘故。这时，只要出现很小一点气流，电流强度就会有相当大的变化。在这种情况下，散布在钍化合物附近空间中的放射性同试样本身的放射性相比，已经不能忽略不计。
用锕做实验，气流的影响更加严重。使用放射性本来很强的锕化合物作试样，当有气流通过时，它变得好似只有弱得多的放射性。
由此推测，气体中应该包含有一种特殊形式的放射性能量。卢瑟福认为，那大概是放射性物质向外散发出来的射气 或者说某种携带着放射性的气体物质。皮埃尔·居里和我的看法则是，说镭产生了一种气体，这种假定至今也还没有得到证实。我们现在只能说，射气不过是以一种目前还不知道的形式蓄积在气体中的放射性能量。
固体的感生放射性在敞开空气中的耗散定律
把一块固体测试板放入一个密闭空间用镭激发足够长时间，然后取出暴露在敞开的空气中。这时，它将按指数定律失去其放射性。感生放射性逐渐消失的这个规律对于任何受到激发的物体都成立，可以表示为下式：
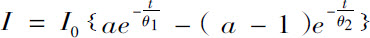
式中I 0 是测试板从密闭空间被取出时刻的初始辐射强度；I 是经过时间t 后的强度；a 是一个数值系数，a ＝4.20；θ 1 和θ 2 是两个时间常数，θ 1 ＝2420秒，θ 2 ＝1860秒。两三个小时之后，上式实际上已经变为一个简单的指数函数，式中第二项指数对I 值的影响已经可以忽略不计。于是，这个放射性耗散定律就可以简单地表述为：辐射强度每过28分钟减小至先前强度的一半。放射性在非密闭的存在着空气的空间逐渐消失的过程最后必然要遵守的这个耗散定律，可以被看成是固体物质被镭激发产生的感生放射性的一个特征。
被锕激发的固体，它们在敞开的空气中也按照上面类似的指数定律失去其放射性，只是耗散过程要慢一些。
被钍激发而具有放射性的固体，放射性消失得更慢，它们的辐射强度要每过11小时才会减小至先前的一半。
放射性在密闭空间内的耗散，射气湮灭的速度
让一个密闭容器内充满某种气体，用镭照射使它获得放射性，然后使其脱离镭的影响。这时，这个密闭容器也会按照一定的规律失去其放射性，但是放射性消失的速度要比在敞开的空气中慢得多。用一只玻璃管进行实验就可以发现这种放射性耗散规律。把玻璃管插入一种镭盐溶液中，与溶液接触一段时间，使它内部获得放射性。取出后迅速用火焰烧熔玻璃管两端，将其封死。然后测量玻璃管在失去其放射性的过程中从它的管壁发出的辐射的强度。
这样测得的耗散规律也是一个指数定律，可以非常精确地表示为 (1)
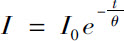
此式中，I 0 是初始辐射强度；I 是在时刻t 的辐射强度；θ 为一个时间常数，θ ＝4.970×105 秒。
辐射强度每过四天减小至先前的一半。
不论在什么实验条件进行实验（密闭空间的尺寸、容器壁的材料、密闭容器内气体的种类、被镭盐溶液作用的时间，等等），得到的都是这个耗散定律，绝不会改变。在从-180℃到＋450℃的温度范围进行的实验表明，无论在什么温度，也仍然是这个耗散定律。因此，这个定律完全可以被看成是被密闭在一个空间中的具有感生放射性的空气的一个特征。
在上述这些实验中，玻璃管壁的放射性是靠蓄积在内部气体中的辐射才得以维持。如果抽出气体，使玻璃管内成为真空，那么，放射性会立即加快散失，辐射强度将变为每过28分钟减小至先前的一半。用普通空气换掉玻璃管内具有放射性的空气，结果也是如此。
由此可见，辐射强度每过四天才减小至一半的耗散定律，其实是蓄积在内部气体中的辐射能的耗散特征。用卢瑟福的话来说，镭散发出来的射气会作为时间的函数自发消失，每过四天减少至先前的一半。
钍散发的射气又是一种类型，消失得要快得多。它的辐射强度大约每过70秒就会减小至先前的一半。
锕的射气消失得更快，每过几秒钟就会减少至先前的一半。
获得放射性的液体和镭溶液的放射性的变化
不论什么液体，只要放入一个具有放射性的密闭空间，都会获得放射性。取出液体，把它暴露在敞开的空气中，液体就会迅速失掉其放射性，并把放射性传播给周围的气体和固体。如果把这样得到的具有放射性的液体放入烧瓶中密封起来，它失去放射性的速度就要慢得多。在这后一种情形，液体的辐射强度每过四天才减小至先前的一半，同在类似条件下气体的放射性减小速度一样。液体和气体的这种类似性似乎向我们暗示，辐射能量保存在液体中的方式大概与它保存在气体中的方式完全相同（以射气的形式保存）。
镭盐溶液在这方面也有类似之处。首先，有一个事实是非常重要的，那就是，在密闭空间内放置的镭盐溶液，如果在此密闭空间内它的旁边还有一个盛有纯水的容器，那么，经过一段时间，在镭盐溶液和纯水之间建立起辐射平衡之后，镭盐的放射性就绝不会比它旁边的纯水强。把镭盐溶液从密闭空间取出，装进敞口容器内暴露在空气中，它的放射性就会散布到周围空间，最后使得溶液几乎没有放射性，尽管溶液中仍然含有镭。此后，如果把这种溶液再装入烧瓶密封起来，它又会重新逐渐得到放射性，并在大约两周后达到一个强度相当大的最大值。至于那些不含镭的液体，尽管可以利用镭的化合物激发使它们也具有放射性，但是，它们一旦暴露在大气中失去放射性，此后再装入烧瓶密封起来，就绝不会重新获得放射性。
放射性理论
这里介绍的是由皮埃尔·居里和德比尔纳阐明的一种普遍适用的放射性理论。这种理论可以把我刚才介绍的关于感生放射性的研究结果同实际观测到的那些不带任何假设的确凿事实协调起来。
按照这种理论，每一个镭原子本身就是一个可以持续不断地产生能量的能源，无须假定这种能量另有来源。积聚在镭中的这种放射性能量有通过两种不同的方式向外散逸的倾向。一种是辐射（带电和不带电的射线）；另一种是传导，即以气体和液体为媒介将能量逐渐传递给周围的物质（产生一种射气并转变为感生放射性）。
放射性物质内部积聚的能量越多，通过辐射和通过传导失去的放射性能量也越多。整个系统必须达到平衡，而在平衡时，镭新产生的能量正好可以补偿这两种方式损失的能量。这种考虑问题的方法类似于研究生成热量的现象。任何物体的内部，如果因某种原因持续不断地有热量产生出来，那么，新生成的热量就会蓄积在物体内而使它的温度升高，直到通过辐射和传导失去更多热量从而与继续不断产生的热量达到热平衡为止。
一般说来，除了在某些特殊环境，放射性能量不能在固体中传导。保存在一根密封管内的溶液，由于此时只能通过辐射失去能量，它的放射性会得到加强。
相反，装在一个敞口容器里的溶液，以传导方式失去的放射性能量相当大，因此在平衡状态下，溶液的放射性会减弱。
暴露在空气中的固体镭盐，它的放射性并未见减弱，这是因为这种固体物质的内部不传导放射性能量，只有它很薄的表层才在产生感生放射性。然而镭盐的溶液则不同，它们会产生非常强的感生放射性现象。固体状态的镭盐，放射性能量被积聚在内部，它主要是通过辐射散逸出去。但是，若把镭盐溶解在水溶液中，不多几天，它的放射性能量就会一部分被分配给盐，而另一部分被分配给水。这时如果通过蒸馏再把两者分离开来，那么，由于水带走了大部分放射性，固体镭盐的放射性就要比溶解前小得多（只有原来的十分之一或十五分之一）。不过，固体镭盐此后还能够逐渐恢复它原来的放射性。
上面的理论还可以更深入一步，即假定镭的放射性不过是镭的原子以散发一种射气的形式释放出放射性能量的一种现象。
我们可以把每一个镭原子都看成是一个正在持续不断地散发射气的射气源。镭原子在产生射气的同时，也就产生了这种形式的能量。射气的能量此后才逐渐转化为贝克勒尔辐射的放射性能，而转化的速度则正比于镭所积聚的射气的数量。
当把一种镭溶液放入一个密闭容器内时，溶液中镭原子产生的射气就在容器内扩散开来，蔓延到容器壁。射气就是在这里转化成辐射。溶液虽然也发出贝克勒尔射线，但数量极少。发出辐射，不过是一种外部效应 。另一方面，在固体镭的情形，射气很难逸出，只能聚集起来，局限在一个很小的范围转化为贝克勒尔辐射。所以，固体镭的辐射具有较高的强度。
上面介绍的这种放射性理论如果普遍成立的话，那么就应该是所有的放射性物质都在产生射气。对于镭、钍和锕，事实的确如此。特别是锕，散发射气的数量还非常大，即使在固体状态也会散发。铀和钋似乎完全不散发射气，虽然它们在产生贝克勒尔射线。这两种物质不会在密闭空间产生感生放射性，这与前面提到其他放射性物质都不同。这个事实也不一定就同上面的理论绝对矛盾。如果铀和钋散发的射气会很快湮灭掉的话，那么，自然就很难观察到这样的射气被空气携带和它们使周围物质产生感生放射性的效应。作这样的假设并非毫无根据，因为一定数量的镭射气和钍射气，如果都减小至一半，两者各自所需要的时间之比是5000∶1。我们在下面还会看到，事实上。在一定条件下，铀也是能够激发出感生放射性的。
感生放射性的另一种形式
镭使附近固体产生的感生放射性，按照在敞开空气中的耗散定律，一天之后就会几乎消失殆尽。
但是也有例外。有一些物质。例如赛璐珞、石蜡、生橡胶等，它们在被镭射线充分作用之后，感应得到的放射性消失的速度要比根据耗散定律的预期慢得多，常常要经过15～20天以后才检测不到。看来，这些物质具有以射气形式储存放射性能的性质。此后，它们会逐渐失去这种放射性能，并使邻近的物质获得感生放射性。
慢耗散感生放射性
此外还有一种形式的感生放射性，这似乎是在密闭的具有放射性的空间保存数个月的任何一种物质都能够获得的一种放射性。从密闭的空间取出这些物质，它们的放射性先是按照正常的耗散定律（半小时减小到一半）减小到一个很小的数值，但是，在减小到大约为初始值的1/20000时，它们的放射性就不再减小了，至少是减小得非常慢，甚至有时还会增大。我们的一些铜片、铝片和玻璃片，在六个月后还仍然残留有放射性。
这些现象似乎揭示出与通常的感生放射性不同的又一种类型感生放射性，它们的演变过程要慢得多。
这种类型的感生放射性，无论感应产生还是耗散消失，都需要很长的时间。
物质在含镭溶液中感应的放射性
为了提取到镭，需要处理含有镭的放射性矿石，通过一系列化学分离过程将原来大量矿石中的放射性全部集中到所得到的众多分离物中的某一种产物上了。这样得到的放射性产物，它们的放射性可以是铀的放射性的数百倍，其中已经把许多物质如铜、锑、砷等以完全不带放射性的状态分离出去了。想要进一步浓缩已经得到的这些放射性物质，由于有一些物质（铁、铅）是无法以完全不带放射性的状态被分离出去的，那就得另想办法。这时，每一次化学分离都不再能够分离出绝对不带放射性的产物。任何一次分离的结果，所得到的所有分离物全都或多或少具有不同程度的放射性。
在发现存在着感生放射性之后，吉塞尔曾最早尝试用放射性物质去激发通常并无放射性的铋，使它感应出放射性。他把没有放射性的铋投入一种具有很强放射性的镭盐溶液中，结果得到了具有放射性的铋。他据此认为，从沥青铀矿中提取到的钋很可能其实是沥青铀矿中含有的镭作用于附近而产生的具有感生放射性的铋。
我把铋制品投入具有很强放射性的镭盐溶液中，也得到了放射性铋。
做这种实验有很大的难度，必须采取措施，务必彻底清除掉溶液中的任何一点镭。我们知道，任何1克本来没有放射性的物质，哪怕只夹杂了极其微量的镭都足以产生非常强的放射性。因此，我们其实很难判断我们从溶液中重新分离出来的那种具有放射性的铋产物是否真的已经得到了彻底清洗和十分纯净。每做一次净化处理都会使放射性减小，然而，这有可能是清除了杂质镭，也有可能是获得了感生放射性的铋在净化过程中也发生了化学反应而有损失。
我的实验结果多半能够肯定，我所得到的铋没有受到镭的污染，的确获得了放射性，而且能够保持这种放射性。我是用加水沉淀的方法来从硝酸盐溶液中分离得到我的放射性铋的硝酸盐。我发现，经过认真的净化处理，铋能够像钋那样被分离出来。放射性最强的这一部分会最先沉淀。
如果净化处理做得不好，沉淀中就仍然夹杂有痕量的镭，实验就会失败。我这样得到的放射性铋，从我的分离过程看，应该是非常纯净的，它的放射性是铀的2000倍。这份铋制品的放射性会随时间而减小。但是，我用相同的净化措施和相同的分离方法所得到的这种产物的另一份制品，它的放射性却在三年后都未见减小，仍然保持了它起初的放射性。
这份制品的放射性是铀的150倍。
把铅和银投入含镭的溶液中，我还得到了具有放射性的铅和银。一般说来，用这种方法得到的感生放射性几乎不随时间而减小。但是，这样得到的放射性物质其后免不了会发生一系列化学变化。
德比尔纳在锕的溶液中放入钡，也得到了具有放射性的钡。他的这种钡在参与了几次化学反应之后还仍然具有放射性。由此看来，它的放射性应该体现的是一种比较稳定的原子特性。德比尔纳提取这种放射性氯化钡所使用的分离方法同钡-镭氯化物的分离相同，这种放射性最大的成分在水和稀盐酸中的可溶性最小。干燥的钡的氯化物会自发发光，它的贝克勒尔辐射类似于钡-镭氯化物的辐射。德比尔纳如此制得的一种具有放射性的氯化钡，其放射性是铀的1000倍。但是，他得到的这种钡并不具有镭的全部特性，在光谱仪上，看不到镭的任何一条最强的谱线。不仅如此，把这种放射性钡静置一旁，它的放射性还会不断减小，三周以后，放射线强度就减小到了只有原来强度的三分之一。
物质在含有放射性物质的溶液中被感应出放射性，这是一个还需要深入加以研究的领域。初步的研究表明，似乎在不同的实验条件下，得到的会是稳定性很不一样的原子感生放射性。在这种情况下感应得到的放射性，也许与那种耗散缓慢，在一个具有放射性的密闭空间内位于较远距离受到长久照射所获得的感生放射性属于同一个类型。我们必须要搞清楚，感生放射性在多大程度上影响到了原子的化学属性，以及它是否能够改变原子的化学性质，不论是暂时改变抑或是永久改变。
对于在较远距离被激发出放射性的物体进行化学研究会相当困难，这是因为，被激发物体的感生放射性仅限于它的表面很薄的一层，结果，物体的全部物质中其实只有很小一部分受到了影响。
把某些物质放入含有铀的溶液中，也可以使它们获得感生放射性。对于钡，已经成功进行了这种实验。德比尔纳所做的这种实验，是把硫酸加入同时含有铀和钡的一种溶液中，在这种情况下得到的硫酸钡沉淀获得了放射性，而铀盐则失去了一部分放射性。贝克勒尔还发现，重复实验多次，甚至可以得到几乎没有放射性的铀。这些实验结果会给人一种印象，似乎有某种不是铀的放射性物质从铀中分离出来了，而铀正是由于含有这种物质才具有放射性。然而事实并非如此。因为，过了几个月，铀又恢复了它原来的放射性，而沉淀出来的硫酸钡则失去了它所获得的放射性。
对于钍，也观察到了类似的现象。卢瑟福利用氨水使一种钍盐的溶液出现沉淀，然后取出溶液，把它蒸发至干。他得到了很少一点残余物，经检测，具有放射性。再检测原来溶液中含有钍的沉淀物，放射性已经减弱。卢瑟福把这种具有放射性的残余物取名为钍X 。过了一段时间后，残余物失去了放射性，而含钍沉淀物恢复了原来的放射性。
总之，在对感生放射性现象进行过的研究中看不到一种统一的模式，不同的物质有不同的表现。有些物质容易获得感生放射性，有些物质则不容易。
实验室里的放射性微粒和感生放射性
在研究强放射性物质时，为了保证能够得到精密的测量结果，必须遵守一套严格的操作规范。在化学实验中和在物理实验中使用的各种物品，过不多久就会获得放射性，能够穿透黑纸使照相底板感光。灰尘中微粒、房间里的空气、衣物等等，全都带有放射性。房间里的空气也变成了电导体。空气成了导体，这给我们的实验室带来很大的麻烦，我们已经没有一件实验用具是完全绝缘的。
因此，必须要采取特别的防范措施，尽最大可能防止在实验室里出现放射性尘粒，并避免感生放射性现象。
绝对不要把化学实验所使用的物品带入进行物理研究的房间，而且尽可能不要在这个房间里留存任何并非必需的放射性物质。我们已经养成一种习惯，在开始用电学法进行实验研究前，总要把实验设备的不同部分用绝缘的金属导线连接起来，再用接地的金属套管把这些导线加以屏蔽，以防止外来电场的干扰。在研究放射性物质时，即使采取这样的预防措施也仍然有漏洞。空气既然成了导体，那么金属导线和金属套管之间就没有完全绝缘，而金属导线和金属套管之间不可避免地总会有接触电动势，这就有可能在两者之间的空气中产生电流，导致静电计偏转。我们现在的做法，是让所有的金属导线都穿过填满了石蜡或其他绝缘材料的金属套管，使它们与空气隔绝。此外，在这类研究中，最好是使用密封良好的静电计。
非放射性物质引起的感生放射性
还有人尝试过不用放射性物质，而用其他方法来产生感生放射性。
维拉德把铋制成克鲁克斯管的对阴极（阳极），使它接受阴极射线的作用。结果，他的实验品铋获得了非常微弱的放射性。用它照射照相底板，需要曝光八天才能得到感光影像。
麦克里南（Maclennan）让几种盐类接受阴极射线的作用，然后加热略微升高它们的温度。经过如此处理的盐类获得了能够将其他带正电物体中和，使之不再带电的性质。
这类研究是很有意义的。如果我们能够采用已知的物理手段使得原来没有放射性的物质产生出比较大的放射性的话，那么，我们或许就有希望由此找到为何某些物质具有自发放射性的原因。
放射性物质放射性的变化，溶液的影响
钋的放射性，如我前面介绍过的，会随时间而减小。这种减小是缓慢的，但是对于不同的试样，它们的放射性并不是以相同的速度减小。我的一份铋-钋硝酸盐试样，它在11个月后失去了一半的放射性，在33个月以后失去了原来95％的放射性。其他的试样，它们的放射性也大致以这种方式减小。
我从硝酸盐制得的另一份含有钋的金属铋试样，它的放射性在刚制得时曾经是铀的100000倍。如今，这份金属铋的放射性已经下降到了具有中等强度（铀的2000倍）。我们会每间隔一段时间就测定一次它的放射性。在六个月中，它失去了67％的放射性。
化学反应大概不会使放射性物质失去放射性。一般说来，快速地经过一系列化学变化之后，放射性并未见有什么损失。
与上述钋的情况不同，镭盐具有稳定不变的放射性，多年后，都没有检测出它们的放射性有所减弱。
刚制得的处于固体状态的镭盐并不是一开始就具有强度稳定不变的放射性。它的放射性从刚制得那一刻起就在一直增大，在大约一个月后达到一个实际上是常量的极限值。镭盐溶液的情况则与此相反。刚制得的镭盐溶液具有很强的放射性，但是，暴露在空气中，它的放射性会迅速减弱，最后达到一个比原来的放射性要小得多的极限值。放射性的这种变化是被吉塞尔最先观察到的，不难用射气理论加以解释。溶液的放射性减弱，是由于有射气散逸到周围空间丢失掉了。如果把溶液装入一只密封管，这种放射性减弱的现象能够很好地得到抑制。在空气中已经损失了放射性的溶液，装入密封管内，还能恢复一部分放射性。最近，我将镭盐溶解在溶液中，再从中提取出固体状态的镭盐，它的放射性随时间而增大。这是因为，在这段时间，固体镭中正在重新积聚起越来越多的射气。
下面来介绍我研究这个问题进行的一些实验。
一种钡-镭氯化物溶液，暴露在空气中，两天后放射性减弱到了1/300。
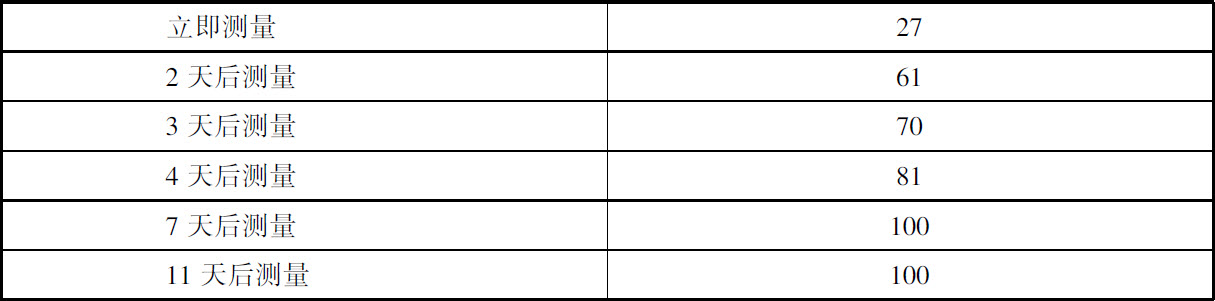
把一种溶液装入一只玻璃管，塞紧管口。过一段时间，打开容器，把溶液倒入一个浅皿，然后测量它在不同条件下的放射性，结果如下表。
把一种曾经在空气中敞开放置了一段时间的一种钡-镭氯化物溶液装入一支玻璃管，密封起来，然后测量玻璃管在不同条件下的放射性，结果如下表。
从溶液制得的固体盐，它的刚制得时的初始放射性取决于它先前溶解在溶液中时间的长短，时间越长，放射性越弱。它的放射性有相当大一部分已经转移给了溶剂。下面给出的数字是我用一种固体氯化物进行实验所测得的它的初始放射性。这种固体氯化物的极限放射性为800。实验中把它这种固体盐分别溶解在溶液中保持不同时间，然后蒸干重新得到固态盐，立即测量它的放射性，结果如下表。
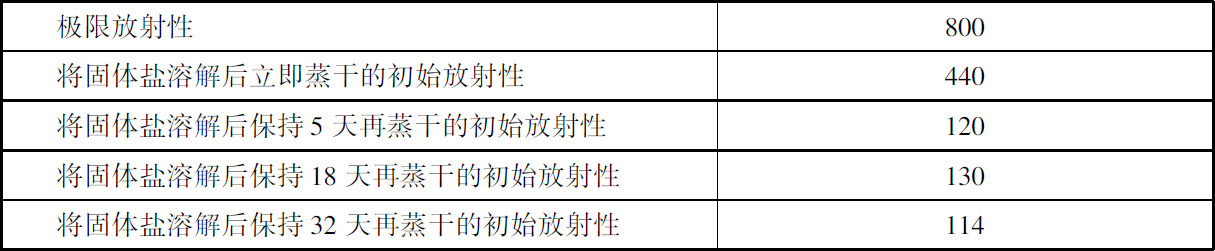
在上述实验中，盛有这种盐溶液的容器仅用一片表面皿盖住。
我利用上述实验中所使用的同样氯化物制备了两种溶液，其中一种溶液的浓度是另一中溶液浓度的8倍。分别放在两只玻璃管内，密封起来，保存13个月，然后蒸干后测量，结果如下表。
显然，在溶剂数量更多的溶液中这种盐的放射性损失会更大，因为要有更多的放射性能量传递给体积更大的液体，才能使后者的更大空间达到能量饱和。所以，这同样一种盐的两份固体试样会有不同的初始放射性。此后，这两份试样的放射性不断增强，但开始时增强的速度差别很大。一天后，两者的放射性强度相同，并以相同的方式继续增强，直至达到这种固体盐的放射性极限。
从下面的实验可以看出，在稀溶液中的盐类，放射性的损失是非常快的。把数量相同的三份同一种镭盐分别溶解在三份等量的水中。把第一份溶液（a ）与空气接触放置一小时，然后蒸干。把空气流通入第二份溶液（b ），经过一小时，然后蒸干。把第三份溶液（c ）敞开在空气中露置13天，然后蒸干。最后分别测量从这三份溶液中得到的三份固体镭盐试样的初始放射性，结果如下表。
上述实验中所使用的那同一种镭盐的极限放射性大约是470。从上面给出的数字可以看出，对初始放射性影响最大的是头一个小时，而且，气流通过溶液b 搅出气泡一小时，影响甚微。实验使用的溶液，其中镭盐比例大约是0.5％。
表现为放射性能量的射气，对于周围是空气的固体形态的镭来说，要从固体向外传播应该是非常困难的。对于浸没在液体中固体镭，也应该如此。一块固体的硫酸镭，即使放入水中晃动一整天，它的放射性同暴露在空气中的同一种硫酸镭并无两样。
把镭盐放入真空，按说，所有能够散逸的射气都应该离开了它。然而，把氯化镭放在真空中保存六天，再作检测，它的放射性几乎丝毫不受影响。这个实验表明，镭盐的放射性主要是来自组成镭盐的那些粒子内部所产生放射性能，那自然不受真空的影响。
镭在溶液中的放射性损失，相对说来，是总辐射中具有穿透性的射线的损失要比可吸收射线的损失更大。下面是关于这个问题的几个例子。
我们把放射性已经达到其极限值470的氯化镭溶解在溶液中，一小时以后，将溶液蒸干，立即用电学法测量如此得到的固体氯化镭的初始放射性。结果发现，总的初始辐射等于其总极限辐射值的0.3。但是，如果用一张0.01mm厚的铝箔隔板将试样盖住，再测量穿过铝箔的辐射强度，那么，测得的穿过隔板的初始辐射便只有穿过这同一块隔板的极限辐射的0.17。
把镭盐溶解在溶液中的时间延长至13天，在这种情况下测得的总的初始辐射是总的极限辐射的0.22，而把两者穿过0.01mm铝箔后的值作比较，前者只等于后者的0.13。
在溶液中溶解时间不同的两种情况，溶解后的初始辐射对极限辐射的比率都要大于这两种辐射穿过0.01mm铝箔后的同一比率，前者为后者的大约1.7倍。
必须指出的是，蒸发溶液重新得到溶解过的试样，必然会有一段时间试样是处于中间状态，在这个状态，它既不完全是固体也不完全是液体。此外，为了尽快脱水，还不得不对试样加热。
由于这两个原因，在实验中几乎不可能测量到试样从溶液回到固态的初始放射性的真实值。在上面介绍的实验中，在溶解时间不同的两种情况，是把等量的放射性物质溶解在相同数量的水中，并在尽可能相同的条件下把溶液蒸干，加热温度不超过120℃或130℃。
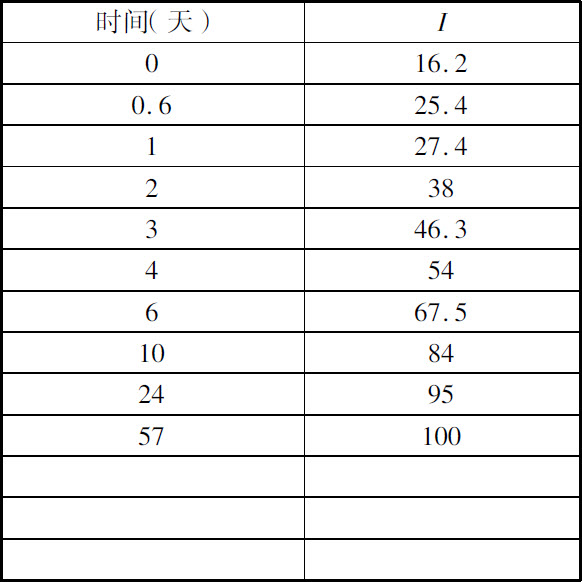
我曾研究过从蒸干溶液得到固体镭盐的时刻到它达到其放射性极限时刻这一期间试样放射性的增强规律。在下面给出的列表中，把辐射强度I 表示为时间的函数，规定极限强度等于100，时间则从试样变干燥开始计算。表I（图12中曲线I）给出的是总辐射值，表Ⅱ（图12中曲线Ⅱ）给出的仅是可穿透射线（穿过了3cm的空气和0.01mm铝隔板的射线）。
表Ⅰ
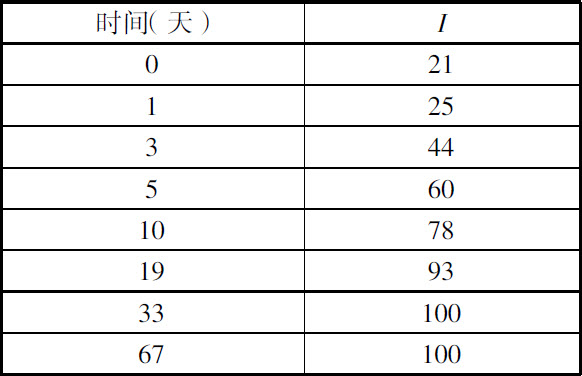
表Ⅱ
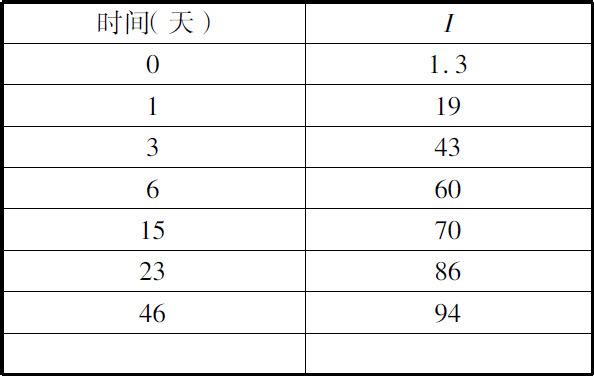
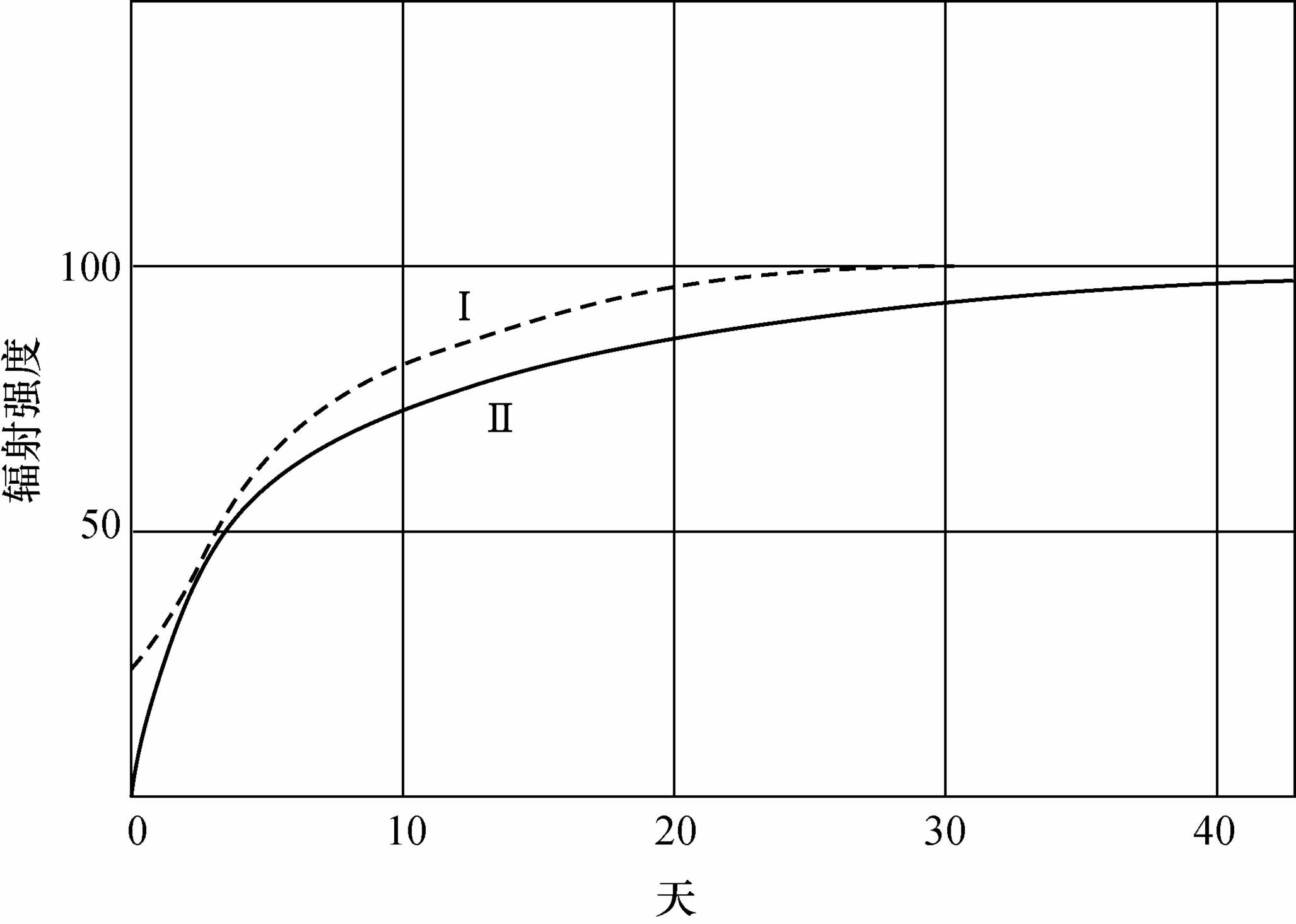
图12
我还对其他试样也进行过这样的对比测量，但得到的结果彼此并不绝对一致，尽管得到的曲线的总体样子相同。要得到非常吻合的结果是非常困难的。这里我仅指出，为了让试样获得它所能达到的全部放射性，常常需要等待不止一个月的时间，而且，穿透性最强的那些射线受溶液的影响最大。
从上面两个例子我们已经看到，能够穿过3cm的空气和0.01mm厚的铝隔板的初始辐射强度只有极限强度的1.3％，而总辐射的初始强度则是总极限辐射的21％。
我有一份一直溶解在溶液中的镭盐，最近才把它蒸干制成固体。这份试样同样也具有引起感生放射性的能力（以及容许射气逸出的能力），而且它的这种能力与另一份在被制成固体以后就长期保持在固体状态，已经获得了极限放射性的镭盐试样不相上下。但是，这两份试样的放射性却差别很大，例如，前者放射性强度要弱得多，只及后者的1/5。
加热引起的镭盐放射性的变化
镭化合物受到加热，会向外散发一种射气，从而失去一部分放射性。加热越剧烈，时间越长，放射性损失就越大。例如，把镭盐加热到130℃保持一小时，它的总辐射会损失掉10％。但是，加热到400℃，时间只有10分钟，则不会产生明显的影响。在炽热状态加热几个小时，则会损失掉总辐射的77％。
加热损失放射性，总辐射中的可穿透射线的损失要比可吸收射线更加严重。例如，加热数小时使总辐射损失掉了77％，而同样的加热却能够使穿过3cm的空气和0.01mm厚的铝隔板的辐射差不多全都损失掉（99％）。把钡-镭的氯化物加热到熔融状态（接近800℃）保持数小时，则会损失掉穿过0.3mm铝隔板的辐射的98％。在高温下长时间加热，实际上能够使辐射中不再有那种具有穿透性的射线。
加热使镭盐失去部分放射性，这种效果不会持久。在常温下，镭盐的放射性又会自行恢复，逐渐增大至某个确定的极限值。我还观察到一个奇怪的事实，这加热后达到的极限值要高于被加热前的极限值，至少对于氯化物是如此。例如，我有一份钡-镭氯化物试样，在制成固体后经过一段长时间，它的总辐射强度用数字表示等于470，其中能够穿过0.01mm铝隔板的辐射等于157。把这份试样加热到炽热状态保持数小时，两个月后，它的放射性再次达到极限，这次测得的总辐射等于690，穿过0.01mm铝隔板后的辐射等于227。我的这份钡-镭氯化物试样经过加热后，与加热前相比，无论总辐射还是穿过铝隔板后的辐射都增大了，增大的比率分别为690/470和227/157。这两个比率其实相等，都等于1.45。
另有一份镭-钡氯化物试样，在制成固体后，最后测得极限放射性为62。把它熔融，保持在熔融状态数小时。凝固后，再研磨成粉末。这份试样逐渐增大其放射性，最后达到一个等于140的新的极限值。这个极限放射性值是先前将溶液经过没有被明显加热的蒸干而得到固体状态的极限放射性值的两倍。
我还研究过镭化合物被加热以后放射性逐渐增大的规律。下面给出的是对总辐射和对可穿透辐射分别进行测量的结果。表I和表Ⅱ中的数字是把辐射强度（I ）表示为时间的函数，并规定极限强度等于100。时间从加热结束时开始计算。表Ⅰ（图13中曲线I）给出的是钡-镭氯化物试样的总辐射强度值。表Ⅱ（图13中曲线Ⅱ）给出的是这份试样的辐射穿过3cm的空气和0.01mm厚铝隔板后的强度值。两份试样都在耀眼的炽热状态下加热7个小时。
表Ⅰ
表Ⅱ
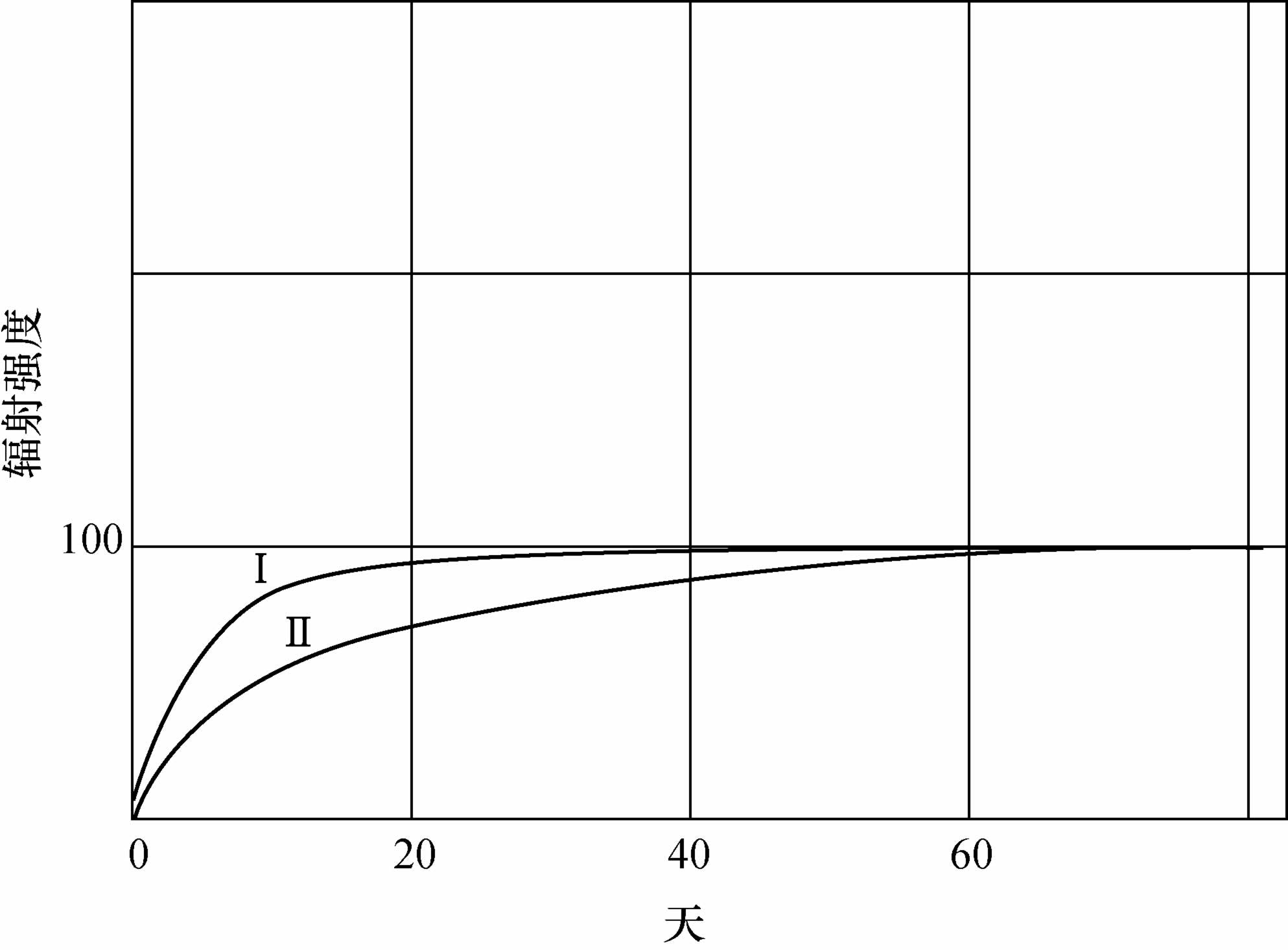
图13
我也测量过其他的试样，所得结果的一致性不是很好。
如果把加热过的镭化合物溶解在溶液中，加热效果会完全消失。我先制备出放射性同为1800的同一种镭化合物的两份样品，把其中的一份剧烈加热，它的放射性因此下降到670。然后，我再把这两份试样各自都溶解在溶液中，保持20小时。最后测量从溶液得到的它们在固体状态下的初始放射性，结果是未加热过的试样为460，加热过的试样为420。显然，两份试样并无显著差别。但是，如果不是把两份镭化合物试样溶解在溶液中保持足够长的时间，比如说，刚一溶解便立即蒸干，那么，没有加热过的那份试样的放射性就要比加热过的试样的放射性强得多。由此可见，必须要处在溶解状态一定的时间，加热效果才会被消除。有一种放射性为3200的镭盐，将它的一份试样加热，结果放射性减小到1030。把这份试样和同一种镭盐的另一份没有加热过的试样各自都溶解在溶液中，然后立即蒸干。对得到的固体测量初始放射性，结果是未加热过的一份试样为1450，加热过的试样为760。
固体的镭盐，它们激发产生感生放射性的能力也会受到加热的极大影响。在被加热期间，镭化合物会比常温状态发出数量更多的射气。但是，再冷却到常温状态，不仅它的放射性要比被加热前小得多，而且感应出放射性的能力也大为下降。不过在加热停止后的一段时间，镭盐的放射性又会逐渐增强，甚至有可能超过原来的强度。它的感应出放射性的能力也会部分地得到恢复。但是，如果长时间地加热到炽热状态，它的这种感应出放射性的能力就会差不多完全丧失，以后也不可能再自行恢复。这时，如果把这种丧失了感生放射性能力的镭盐溶解在水中，然后在烤箱中在120℃下蒸干，则有可能使它重新获得这种能够感应出放射性的能力。这种处理，就好像把镭盐置于一种特殊的物理条件，在这种特殊条件下，它要比未曾加热到过高温的同一种固体试样更不容易散发射气，因而也就能够达到比被加热前更高的放射性极限。要使镭盐转变到它被加热前的这种物理状态，只需把它溶解，再在加热不超过150℃的温度下蒸发至干。
下面是几个实验研究例子。
有一份放射性为1600的钡-镭的碳酸盐试样，它在一个密闭容器内作用于铜板，后者得到的感生放射性极限用a 来表示。
设这份试样未被加热前所产生感生放射性极限a ＝100，被加热后测得结果如下。
加热使钡-镭碳酸盐的放射性损失了90％，但在随后的一个月又恢复到了原来的强度值。
在另一个例子中，是使用钡-镭的氯化物做同样的实验，试样的放射性为3000。用上述实验同样的方法测量它的感应出放射性的能力。
仍然规定加热前的钡-镭碳酸盐所产生的铜板的放射性极限a ＝100。
测量的是钡-镭碳酸盐试样在炽热状态被加热3小时的感应出放射性的能力。
对溶解和加热后镭盐的放射性发生变化原因的理论解释
上面介绍的这些事实，在一定程度上可以根据镭的能量是以射气的形式产生出来，然后再转化成辐射能的理论来加以解释。镭盐溶解后，它所产生的射气蔓延开来，扩散到溶液的外面，从而使得在没有这种放射性源的地方也有了放射性。在溶液被蒸干以后，所得到的固体镭盐只有微弱的放射性，这是因为此时它内部只含有数量很少的射气。此后，镭盐中慢慢重新积聚起越来越多的射气，使它的放射性上升，最后达到一个极限值。达到这个极限值，表明镭所产生射气已经正好能够补偿射气向外散发以及在各个位置就地转变为贝克勒尔射线所造成的损失。
镭盐被加热时，向外散发的射气大量增加，所以，它所感应的放射性现象要强于在常温状态下的镭盐。当镭盐回到常温状态时，类似于在溶液中的情形，它的射气已经消耗殆尽，内部只包含有少量的射气，它的放射性自然就大为减弱。此后，又有射气在固体镭盐内重新积聚，于是辐射逐渐增强。
可以认为，镭总是在稳定不变地产生出射气，其中一部分散逸到外部，剩下的部分便在镭自身内部转化为贝克勒尔射线。把镭加热到炽热状态，它会丧失掉大部分感应出放射性的能力，那也就是说，它向外散发的射气减少了。在这种情况下，镭自身使用射气的比例就应该相应增大，因此，放射性物质能够达到一个更高的放射性极限。
下面，我们来从理论上推导出固体镭盐在被溶解或者被加热后其放射性增大的规律。我们姑且假定，在每一个时刻，镭所发出的辐射的强度都与当时存在于镭内部的射气数量q 成正比。我们知道，射气自发湮灭的规律是使得镭内部在每一时刻所包含的射气数量按照下式减少：
式中q 0 是观测开始时刻的射气量；θ 是一个时间常数，等于4.97×106 秒。
设Δ表示镭在单位时间内所产生的射气量，我们假定它是一个常量。现在，我们来考虑如果没有射气散逸到外部，将会是怎样一种情况。这时，所产生的全部射气都将被镭用来产生辐射。由式（1），我们得到
θ在平衡状态，镭内部应该有确定数量的射气Q，即有
于是，镭发出的辐射应该与Q 成正比。
我们再考虑镭处在一种正在向外部散发射气的环境，又将是怎样一种情况。这种环境，也就是镭化合物溶解在溶液中或者被加热的环境。这时，平衡被打破，镭的放射性将下降。但是，一旦消除了导致射气损失的那种原因（放射性物质恢复到固体状态或者停止加热），射气又会在镭内部重新积聚起来，而且，会有一段时间射气产生的速度Δ超过它们湮灭的速度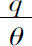
。于是我们有
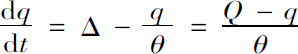
从而得到
式中q 0 为在时刻t ＝0时镭内部包含的射气量。
式（3）表明，镭在平衡状态下所包含的射气量Q 超过在给定时刻它所包含的射气量q 的多出部分是时间的函数，按指数律减小。这也就是射气自发消失的规律。镭发出的辐射正比于内部所包含的射气量，而极限辐射强度超过实际辐射强度的部分应该按照同样的指数律减小。例如，这超过部分大约每过四天减小至一半。
上面介绍的这个理论并不完善，因为讨论中忽略了射气向外部散逸的损失。同时，想要确定射气损失如何随时间而减小也很困难。把实验结果同和这个不完善的理论的结果加以比较，缺乏令人满意的一致性。但是我们仍然相信，这个理论至少有一部分反映了真实。极限放射性超过实际放射性的部分每过四天减小至一半的这个规律近似反映了放射性在加热后10天内逐渐得到恢复的过程。放射性在溶解后得到恢复的过程，至少在从蒸发至干后的头两三天起到10～15天这段时间也是大致符合这个规律的。溶解和加热后放射性发生变化的现象在其他方面也很复杂，比如说，上面这个粗略的理论还不能解释可穿透射线比起可吸收射线来为何受到的抑制会更大的原因。
————————————————————
(1) 原文下面公式中指数漏一负号，现已补上。——校者注
