第四章　平面中的面积论

Chapter IV. Theory of Plane Area

§18　多边形的剖分相等和拼补相等

本章所根据的公理和第三章一样，即连续公理之外的全体直线的和平面的公理，亦即公理Ⅰ_1～3 ，Ⅱ～Ⅳ。

第三章中所阐明的比例论，和那里所引进的线段计算，使得我们有可能用上述的公理，即在平面中而又不用连续公理 ，来建立欧几里得的面积论。

既然按照第三章中的探讨，比例论的主要根据是巴斯噶定理（定理40），所以面积论也如此。面积论的如此建立，在我看来，是巴斯噶定理在初等几何中最突出的应用之一。

定义 　若一个简单的多边形P 的两点用任意一条折线段连接，而这折线段整个的在这多边形的内部，且不含有重点，那么就产生两个新的简单的多边形P ₁ 和P ₂ ，它们的内点都在P 的内部；我们说：P 分割成 P ₁ 和 P ₂ ，或者剖分成 P ₁ 和 P ₂ ，或者P ₁ 和 P ₂ 合并成 P ^【49】 。

定义 　若两个简单的多边形都能剖分成有限多个三角形，而且这些三角形成对的互相合同，这两个多边形就说是剖分相等 。

定义 　若两个简单的多边形P 和Q 能够给添加有限多个这样的成对的剖分相等的多边形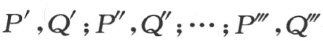 合并，使得按下列方式合并成的多边形 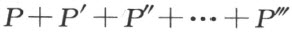和 互相剖分相等，P 和Q 就说是拼补相等 （图53）。

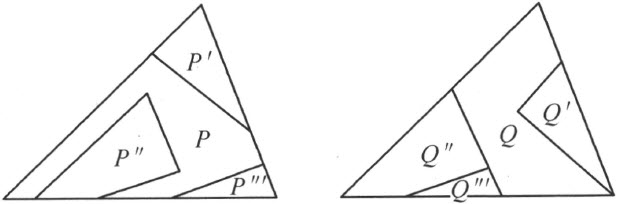
图　53

从这些定义立刻知道：若剖分相等的多边形各拼合上剖分相等的多边形，结果仍然剖分相等 ；若剖分相等的多边形中各去掉剖分相等的多边形，剩下的就拼补相等 （参看补篇Ⅲ）。

下述定理还成立：

定理43  若两个多边形P ₁ 和P ₂ 都和第三个多边形P ₃ 剖分相等，则它们也剖分相等。若两个多边形都和第三个多边形拼补相等，则它们也拼补相等。

证明 　从假设，P ₁ 和P ₃ 各有一个分成三角形的剖分，它们的诸三角形成对的合同；而且P ₂ 和P ₃ 也各有一个如此的剖分（图54）。同时考虑P ₃ 的这两个剖分，在一般的情形下，一个剖分中的每一个三角形被另一个剖分中的诸线段分成若干个多边形。再作适当多条线段，把这些多边形的每一个都分成三角形，而且在P ₁ 和P ₂ 中分别作对应的分成三角形的剖分，然后，P ₁ 和P ₂ 这两个多边形显然分成了同样多的成对的合同三角形，因此，按照定义，彼此剖分相等。

图　54

定理43的第二句话的证明不会发生困难^【50】 （参看补篇Ⅲ）。

下列概念的定义和通常的一样：长方形、平行四边形的底边 和高线，三角形的底边 和高线 。

§19　等底边和等高线的平行四边形和三角形

下面的图（图55）所表明熟知的欧几里得的证明给我们下述定理：

图　55

定理44 　等底边等高线的两个平行四边形拼补相等。

再者，有下述熟知的事实：

定理45 　任意一个三角形ABC 和某一个等底边而半高线的平行四边形剖分相等。

证明 　（图56）二等分边AC 于点D ，边BC 于点E ，其次延长线段DE 两倍长到F ，于是三角形DCE 和FBE 合同，从而三角形ABC 和平行四边形ABFD 剖分相等。

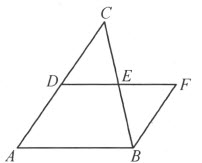
图　56

从定理44和定理45，再参考定理43，即得下述定理：

定理46 　等底边等高线的两个三角形拼补相等 。

大家都知道，下述事实是容易证明的，如同附图（图57）所表出的：等底边等高线的两个平行四边形，因而，从定理43和定理45，等底边等高线的两个三角形，恒剖分相等 ，然而我们要注意，这种证明不用阿基米德公理是不可能的 ；事实上，在每一种非阿基米德几何（例如第二章§12中的一种这样的几何）中，能给出两个三角形，它们等底边又等高线，因而从定理46它们拼补相等 ，但是它们却不剖分相等 ，为证实这句话，设在一种非阿基米德几何中，在一条射线上取两条这样的线段AB ＝e 和AD ＝a （图58），使得没有整数n 适合下列关系：

n ·e ≥a

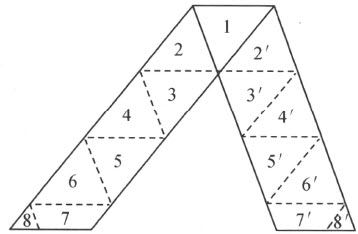
图　57

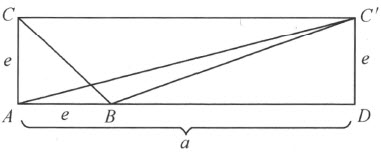
图　58

在线段AD 的两端点处，作长等于e 的垂直线段AC 和DC ′。根据定理46，三角形ABC 和ABC ′拼补相等。从定理23得：三角形的两边的和大于第三边，这里所说的两边的和是按照第三章中所引进的线段的计算来理解的。

因此，BC <e ＋e ＝2e 。再者，不用连续性能证明：一条完全在三角形内部的线段小于这个三角形的最长的边^【51】 。因此，每一条在三角形ABC 内部的线段也小于2e 。

假设三角形ABC 和ABC ′能剖分成有限多个（如k 个）成对的合同三角形。三角形ABC 的剖分中的每一个子三角形的每一条边，或者在三角形ABC 内，或者在ABC 的一条边上，这就是说，它小于2e 。所以，每一个子三角形的周长小于6e ；全体周长的和因而小于6k ·e 。三角形ABC 的这个剖分中的诸子三角形的周长的和必定等于三角形ABC ′的这个剖分中的诸子三角形的周长的和，所以三角形ABC ′的剖分中所用的子三角形的周长的和必定也小于6k ·e ，这个和一定含有整个的AC ′这条边，这就是说：应该有不等式AC ′<6k ·e ；在这情形下，由于定理23，更应该有不等式a <6k ·e 。但是，这后面的关系与我们关于线段e 和a 的假设相矛盾。于是，假设三角形ABC 和ABC ′能剖分成成对的合同子三角形，就发生矛盾。

在初等几何中关于多边形拼补相等的重要定理，特别是毕达哥拉斯定理，都是上文所列出的诸定理的浅易推论。我们还提出下述定理：

定理47 　对于任意一个三角形（因而任意一个简单的多边形），恒有一个与它拼补相等的、一股等于1的直角三角形。

关于三角形的论断，根据定理46，定理42和定理43容易推出^【52】 。关于多边形的论断，可如下证明。剖分简单的多边形成三角形，对于这些三角形决定和它们拼补相等且一股等于1的诸直角三角形，由于这些长度等于1的股可以看做是这些三角形的高线，然后再利用定理43和定理46合并这些三角形，就证明了我们的论断^【53】 。

要进而完成面积的理论，我们面临着一个本质上的困难。特别是我们此前的讨论中，没有断定是否所有的 多边形都拼补相等。若都拼补相等，则此前证明的定理并未告诉我们什么，而且无意义。关键的问题是：两个拼补相等的长方形若有一公共边，是否另一边也必定合同。

只要再详细地研究就会知道，要解答上述的问题，我们需要定理46的逆定理，即下述的定理：

定理48 　若两个拼补相等的三角形有相等的底边，则它们也有相等的高线。

这条基本定理48是欧几里得 《几何原本》第一卷中的第39条定理。在证明这条定理时，欧几里得求助于下述普遍的关于量的原理：整体大于它的部分。这就等于引进了一条新的关于拼补相等的几何公理 ^（1） 。

现在我们能够不用这样的一条新公理来证明定理 48。因而能够按照我们所计划的方式 ，即只用平面公理而不用阿基米德公理 ，来建立面积论 。要想了解这个，我们需要引进面积的度量概念。

§20　三角形和多边形的面积的度量

定义 　在平面几何中，一条直线AB 分布在这直线上的点为两个区域，这两个区域中的一个称为在从A 出发的射线AB 或“有向线段 AB ”之右 ，而且在从B 出发的射线BA 或“有向线段 BA ”之左 ；另一个称为在射线AB 之左，而且在射线BA 之右。对于两条有向线段AB 和AC 来说，若B 和C 都在从A 出发的同一条射线上，在有向线段AB 和AC 之右的区域是同一个（而且反过来也对）。若对于一条从点O 出发的射线g 来说，右区域已经确定了，而且一条从点O 起的射线h 在这区域中，由直线h 所决定的两个区域中那含有射线g 的一个称为在 h 之左 。我们知道，在平面几何中，这样的从一条确定的射线AB 出发，就唯一地规定了每一条射线或每一条有向线段的左右侧^【54】 。

一个三角形ABC 的内部的点或者在边AB ，BC ，CA 之左，或者在CB ，BA ，AC 之左。在第一种情形下，我们说ABC （或者BCA 或者CAB ）是这三角形的正周向 ，而且CBA （或者BAC 或者ACB ）是负周向 ；在第二种情形下，我们说CBA 是这三角形的正周向，而且ABC 是负周向。

定义 　若在以a，b ，c 为边的三角形ABC 中作高线h _a ＝AD ，h _b ＝BE （图59），根据定理41，从三角形BCE 和ACD 的相似即得到比例

a ：h _b ＝b ：h _a

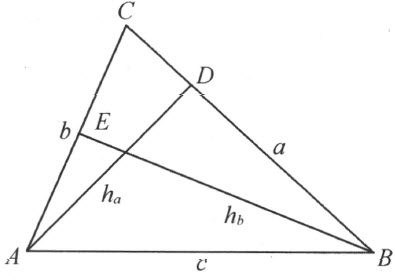
图　59

即

ah _a ＝bh _b

因而，在每一个三角形中一条底边和它对应的高线的乘积和所选取的底边无关。因此底边和高线的乘积的一半是这三角形的一条特征线段a 。设在三角形ABC 中，周向ABC 是正的。这正 线段a （根据本书上的定义）现在就称为正周向的三角形ABC 的面积度量 ，用［ABC ］表示；负 线段-a 称为负周向的三角形ABC 的面积度量 ，用［CBA ］表示。

然后下述的简单定理成立：

定理49 　若一点O 在三角形ABC 的外部（图60），则这三角形的面积度量有下列关系：

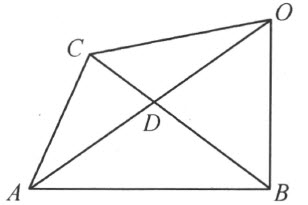
图　60

［ABC ］＝［OAB ］＋［OBC ］＋［OCA ］

证明 　首先，假设线段AO 和BC 交于一点D 。从面积度量定义，用线段计算的分配律，得到

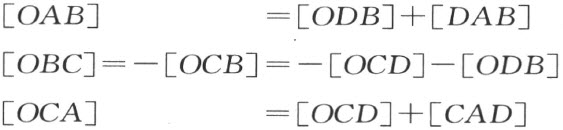
把这些方程中所提到的线段加起来，而且用本书上所提到的一条定理^【54a】 ，就得到

［OAB ］＝［OBC ］＋［OCA ］＝［DAB ］＋［CAD］

由此，再根据分配律，推得：

［OBC ］＝［OBC ］＋［OCA ］＋［ABC ］

在关于点O 的位置的其他假设下，同样可以证明定理49的论断。

定理50 　若一个三角形ABC 任意地剖分为若干个三角形△k ，则正周向的三角形ABC 的面积度量就等于全体正周向的三角形△k 的面积度量的和。

证明 　设三角形的正周向是ABC （图61）。设DE 是三角形ABC 内部的一条线段，而且是剖分中的两个三角形DEF 和DEG 的公共边。设DEF 是三角形DEF 的正周向，那么GED 是三角形DEG 的正周向。现在在三角形ABC 外取一点O ；根据定理49，下列关系成立：

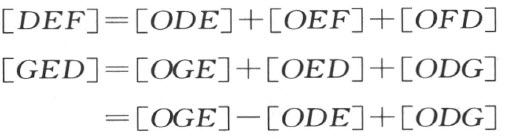
图　61

这两个线段方程相加时，在右端的面积度量［ODE ］消去了。

根据定理49，把全体正周向的三角形△k 的面积度量都这样地写出来，把这些这样得到的线段方程都加起来。在右端中，从三角形内部中的每一条 线段DE 所作成的面积度量［ODE ］都消去了。把三角形ABC 的剖分中所用的、在这三角形的边上的点，依次用A ，A ₁ ，…，A _l ，B ，B ₁ ，…，B _m ，C ，C ₁ ，…，C _n 表示，而且把全体正周向的三角形△k 的面积度量的和简单的叫做∑。容易看出，当所有的线段方程加起来时，就得到：

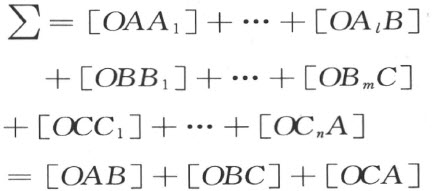
因而根据定理49，

∑＝［ABC ］

定义 　一个正周向的简单多边形的面积度量［P ］定义如下：取这多边形分为三角形的一个确定的剖分，然后定义［P ］为所有这些正周向的三角形的面积度量的和。根据定理50，而且运用和§18中定理43的证明的相似方法，即可知面积度量［P ］和如何剖分成三角形的方式关系，因而只由这个多边形自身唯一决定^【55】 。

从这个定义，再根据定理50，即得：剖分相等的多边形的面积度量相等 。（此处和此后，说到面积度量，都指正周向的多边形的面积度量^【56】 。）

再者，若P 和Q 是拼补相等的多边形，则根据定义必有成对的剖分相等的多边形P ′，Q ′，…，P″ ，Q″ ，使得由P ，P ′，…，P″ 所拼成的多边形P ＋P ′＋…＋P″ 和由Q ，Q ′…，Q″ 所拼成的多边形Q ＋Q ′＋…＋Q″ 剖分相等，从方程

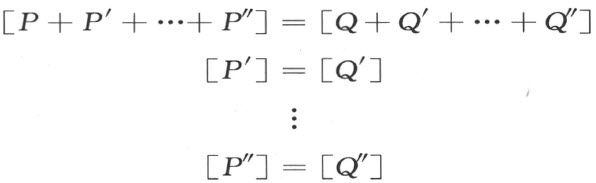
容易得到

［P ］＝［Q ］

即拼补相等的多边形的面积度量相等 。

§21　拼补相等和面积度量

在§20中已经证明了拼补相等的多边形的面积度量恒相等。由此可得定理 48的证明 。用g 表示这两个三角形的相等底边，用h 和h′ 表示相应的高线；从所假设的这两个三角形的拼补相等，即得到它们的面积度量也相等，即

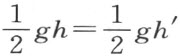
再除以 ，得到

h ＝h ′

这就是定理48的论断。

现在，我们也能证明§20的末尾的论断的逆定理。事实上，设P 和Q 是面积度量相等的两个多边形，根据定理47作具有下述性质的两个直角三角形△和E ：每一个都有一股等于1，而且三角形△和多边形P 拼补相等，三角形E 和多边形Q 拼补相等。从§20的末尾的定理，即得△和P 的面积度量相等，E 和Q 的面积度量也相等。因为P 和Q 的面积度量相等，所以△和E 的面积度量也相等。既然这两个直角三角形都有一股等于1，因此它们的另一股必然也相等，即这两个三角形△和E 合同，因而根据定理43这两个多边形P 和Q 拼补相等。

本节和前节中所求得的两个事实，综合成下述定理：

定理51 　拼补相等的两个多边形面积度量相等，而且面积度量相等的两个多边形拼补相等。

特别地，若两个拼补相等的长方形有一条公共边，则另一边必相等。还得到下述定理：

定理52 　设用直线把一个长方形分成若干个三角形。只要去掉了其中的一个三角形，其余的三角形就不可能填满这长方形。

德左尔特 （de Zolt） ^（2） 和斯铎尔兹（O. Stolz） ^（3） 都用这条定理作为公理，后来舒尔 （F. Schur） ^（4） 和克林 （W. Killing） ^（5） 借助于阿基米德公理证明了它。上文我们证明了，这条定理完全不依赖于阿基米德公理 。

在定理48，定理50，定理51的证明中，主要用了在第三章§15中所引进的线段计算，而且既然这计算主要是根据巴斯噶定理（定理40），或者更确切地说，根据这定理的特殊情形，所以巴斯噶定理是面积论的最重要的基石。

容易看出，也能够反过来从定理46和定理48得到巴斯噶定理。事实上，从直线CB ′和C ′B 的平行（图62），由定理46得知三角形OBB ′和OCC ′拼补相等；同样地，从直线CA ′和AC ′的平行，得知三角形OAA ′和OCC ′拼补相等，所以三角形OAA ′和OBB ′也互相拼补相等，从定理48得知，直线BA ′和AB ′也必定平行。

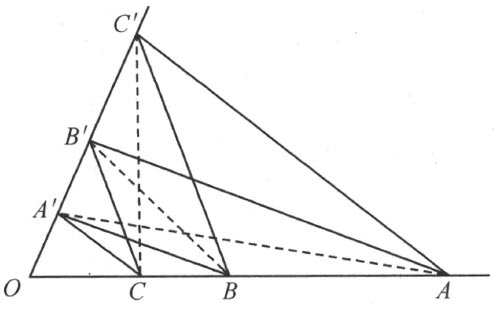
图　62

再者，容易看出，若一个多边形整个的在另一个多边形的内部中，则前者的面积度量小于后者的面积度量，而且根据定理51，这两个多边形不拼补相等。定理52是这个事实的特殊情形。

于是我们建立了平面上面积论的主要定理。

高斯 （Gauss）已经使数学家注意到空间中相应的问题。我曾经猜测在空间中类似地建立体积论是不可能的，而且提出下述具体的确定的问题 ^（6） ：求出具有下述性质的等底面和等高线的两个四面体；它们不能剖分成合同的四面体，而且它们也不能在拼补上合同的四面体之后，作成能剖分成合同的四面体的多面体。

戴恩 ^（7） 成功地得到证明；他严密地证明了，如同上文中建立平面上的面积论的方式，建立空间中的体积论是不可能的。

因此，在处理空间中的类似问题时，必须求助于别种方法，如卡瓦列利（Cavalieri）原理 ^（8） 。

在这种意义下，舒士（W. Süss） ^（9） 建立了空间中的体积论。舒士用下列名称：若两个四面形有等高线和拼补相等的底面，它们就叫做卡瓦列利式相等；若两个多面体能剖分成有限多成对的卡瓦列利式相等的四面体，它们就叫做卡瓦列利式剖分相等；最后，若两个多面体能表为卡瓦列利式剖分相等的多面体的差，它们就叫做卡瓦列利式拼补相等。然后不用连续公理，能证明体积度量相等和卡瓦列利式拼补相等是等价的概念；而只有用阿基米德公理，才能证明体积度量相等的多面体也卡瓦列利式剖分相等。

对于平面而言，自定理51以及本书的思考（紧接定理46之后）就得出定理：任意两个拼补相等的多边形也必剖分相等。这里特别提到西得来（J. P. Sydler） ^（10） 最近所得到的一个结果：在阿基米德公理的假设下，上述定理能推广到空间中的多面体上去。由此，又可以推出下述结论：对于剖分相等而言，多面体的等价类的集合具有连续统的势。

————————————————————

（1） 实际上，我们要在附录Ⅱ中建立一种几何。在这种几何中，除去公理Ⅲ，（这条公理Ⅲ，将被另一条较弱的形式替代）外，这里所根据的公理Ⅰ～Ⅳ都满足了，但是，在这种几何中的定理48，从而命题“整体大于它的部分”不成立。

（2） “在几何等价理论上，关于多边形相等的原理”（Principü della eguaglianza di poligoni preceduti da alcuni critici sulla teoria della equivlenza geometrica. Milano, Briola 1881）。也参看“关于多面体和球面多边形相等的原理”（Principü della eguaglianza di poliedri e di poligoni. Milano, Briola 1883）。

（3） Monatshefte für Math. Und phys., 卷5，1894。

（4） Sitzungsberichte der Dorpater Naturf. Ges. 1892。

（5） Grundlagen der Geometrie，卷2，章5，§5，1898。

（6） 参看我的报告“数学问题”第三。

（7） 戴恩“关于等体积多面体”（Über raumgleiche Polyeder, Göttinger Nachr. 1990）和“关于体积”（Über den Rauminhalt, Math. Ann., 卷55，1902）；再参看Kagan. Math. Ann.，卷57［后一篇论文中有可能的最简单的证明，参看俄文文献：B. φ.KaraH“关于多面体的变换”——单行本，初版，1913年。 出版，和再版1933年 出版——俄译者注］。

（8） 对于空间，只是定理51的第一部分，定理48，定理52，有类似的定理成立；可参看沙突诺夫斯基（Schatunowsky, C. O. ）“关于多面体的体积”（Über den Rauminhalt der polyeder, Math. Ann.，卷57）。戴恩在论文“关于球面三角形的面积”（Über den Inhalt sphärischer Dreiecke Math. Ann.，卷60）中指出：建立平面上的面积论也可不用平行公理，而只用合同公理。还参看芬奇尔（Finzel）“一般几何中面积的理论”（Die Lehre Vom Flächeninhalt in der allgemeinen Geometrie, Math. Ann.，卷72）。

（9） “多面体体积理论的基础”（Begründung der Lehre vom Polyederinhalt, Math. Ann.，卷82）。

（10） 西得来“关于多面体的剖分”（Sur la decomposition des Polyèdres．Comm．Helv．16, 266—273，1946/44）。