《热的解析理论》导读

（北京大学　郭敦仁　孙小礼）

·Chinese Version Introduction·

《热的解析理论》是记载着傅立叶级数与傅立叶积分的诞生经过的重要历史文献，在数学史，乃至科学史上被公认为是一部划时代的经典性著作。

拿破仑·波拿巴

傅立叶：一首数学的诗

傅立叶（Jean-Baptiste-Joseph Fourier, 1768—1830）是法国数学家和物理学家，1768年3月21日生于法国欧塞尔（Auxerre），1830年5月16日卒于巴黎。著名的傅立叶级数和傅立叶积分是19世纪杰出的数学创造，它深刻地影响了19世纪乃至20世纪的数学物理学以及数学的各个领域的发展，同时，人们也公认傅立叶的成果是极优美的数学作品，被称颂为“一首数学的诗”。

生平简述

傅立叶出身平民，父亲是位裁缝。9岁时双亲亡故，以后由教会送入镇上的军校就读，表现出对数学的特殊爱好。他还有志于参加炮兵或工程兵，但因他家庭地位低贫而遭到拒绝。后转至巴黎，希望在更优越的环境下追求他有兴趣的研究。可是法国大革命中断了他的计划，于1789年回到家乡欧塞尔的母校执教。

在大革命期间，傅立叶以热心地方事务而知名，并因替当时恐怖行为的受害者申辩被捕入狱。出狱后，他曾就读于巴黎师范学校（Ecole Normale），虽为期甚短，却给人留下深刻印象。1794年，当巴黎综合技术学院（Ecole Polytechnique）成立时，他被任命为助教，协助拉格朗日（J-L. Lagrange, 1736—1813）和蒙日（G. Monge, 1746—1818）从事数学教学。这一年他还讽刺性地被当做罗伯斯庇尔（Robespierre, 1758—1794）的支持者而被捕，经同事营救获释。1898年，蒙日选派他跟随拿破仑远征埃及。在开罗，他担任埃及研究院的秘书，并从事许多外交活动，但是，同时他仍不断地进行个人的业余研究。

1801年回到法国后，傅立叶希望继续执教于巴黎综合技术学校，但因拿破仑赏识他的行政才能，任命他为伊泽尔（Isère）地区首府格勒诺布尔（Grenoble）的高级官员，由于政绩卓著，1808年拿破仑又授予他男爵称号。此后几经宦海浮沉，1815年，傅立叶终于在拿破仑百日王朝的尾期辞去爵位和官职，毅然返回巴黎以期全力投入学术研究。但是，失业、贫困以及政治名声的落潮，这时的傅立叶处于一生中的最艰难时期。由于得到昔日同事和学生的关怀，为他谋得统计局（bureau of statistics）主管之职，工作不繁重，收入足以为生，使他得以继续从事科学研究。

1816年，傅立叶被选去重组科学院（Académie des Sciences）。初时因怒其与拿破仑的关系而为路易十八所拒。后来，事情澄清，于1817年重新被任命，其声誉又随之迅速上升。他的任职得到了当时年事已高的拉普拉斯（P-S. Laplace, 1749—1827）的支持，却不断受到泊松（S-D. Poisson, 1781—1840）的反对。1822年，他被选为科学院的终身秘书（secrétaire perpétuel），这是极有权力的职位。1827年，他又被选为法兰西学院（Académie Française）院士；还被英国皇家学会选为外国会员。

傅立叶一生为人正直，他曾对许多年轻的数学家和科学家给予无私的支持和真挚的鼓励，从而得到他们的忠诚爱戴，并成为他们的至交好友。他帮助过的科学家中，有知名的奥斯特（H. C. Oersted, 1777—1851），狄利克雷（P. G. L. Dirichlet, 1805—1859）、阿贝尔（N. H. Abel, 1802—1829）和斯特姆（J. C. F. Sturm, 1803—1855）等人。有一件令人遗憾的事，就是傅立叶收到伽罗瓦（E. Galois, 1811—1832）的关于群论的论文时，他已病情严重而未阅，以致论文手稿失去下落。

傅立叶去世后，在他的家乡为他树立了一座青铜塑像。20世纪以后，还以他的名字命名了一所学校，以示人们对他的敬重和纪念。

杰出的科学成就

傅立叶的科学成就主要在于他对热传导问题的研究，以及他为推进这一方面的研究所引入的数学方法。早在远征埃及时，他就对热传导问题产生了浓厚的兴趣，不过主要的研究工作是在格勒诺布尔任职期间进行的。1807年，他向科学院呈交了一篇很长的论文，题为《关于热传导的研究报告》（Mémoire sur la propagation de la chaleur），内容是关于不连续的物质和特殊形状的连续体（矩形的、环状的、球状的、柱状的、棱柱形的）中的热扩散（即热传导，笔者注）问题。其基本方程是：

这是三维情形。

在论文的审阅人中，拉普拉斯、蒙日和拉克瓦（S. F. Lacroix, 1765—1843）都是赞成、接受这篇论文的。但是遭到了拉格朗日的强烈反对，因为文中所用如下的三角级数（后来被称为傅立叶级数）

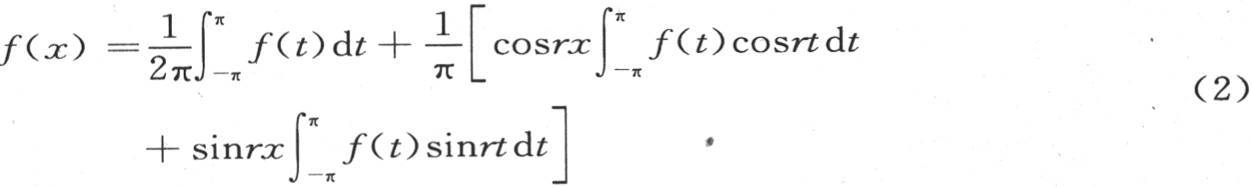
表示某些物体的初温分布，这与拉格朗日自己在18世纪50年代处理弦振动问题时对三角级数的否定相予盾。这篇文章因此而未能发表。不过，在审查委员会给傅立叶的回信中，还是鼓励他继续钻研，并将研究结果严密化。

为了推动对热扩散问题的研究，科学院于1811年悬赏征求论文。傅立叶呈交了一篇对其1807年的文章加以修改的论文，题目是《固体中的热运动理论》（Théorie du mou vement de la chaleur dans les corps solides），文中增加了在无穷大物体中热扩散的新分析。但是在这一情形中，傅立叶原来所用的三角级数因具有周期性而不能应用，于是，傅立叶代之以如下的积分形式，后来被称为傅立叶积分：

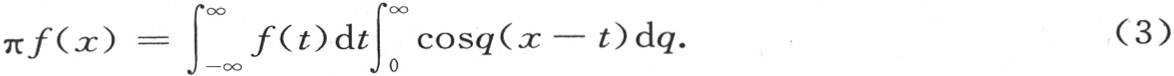
这篇论文在竞争中获胜，傅立叶获得科学院于1812年颁发的奖金。但是评委——可能是由于拉格朗日的坚持——仍从文章的严格性和普遍性上给予了批评，以致这篇论文又未能正式发表。傅立叶认为这是一种无理的非难，他决心将这篇论文的数学部分扩充成为一本书。他终于完成了这部书：《热的解析理论》（Théorie analytique de la chaleur），于1822年出版。他原来还计划将论文的物理部分也扩充成一本书，名为《热的物理理论》（Théorie physique de la chaleur）。可惜这个愿望未能实现，虽然处理热的物理方面的问题也是他得奖论文中的重要内容，而且在他晚年的研究工作中甚至是更重要的内容。

《热的解析理论》是记载着傅立叶级数与傅立叶积分的诞生经过的重要历史文献，在数学史，乃至科学史上被公认为是一部划时代的经典性著作。然而，对于傅立叶在数学上和数理物理上工作的具体评价，历来众说纷纭。有些人只注意了傅立叶级数和傅立叶积分本身的推导，从非时代的严格性标准来要求他。实际上，要全面理解傅立叶的成就，还应该注意到以下两个方面：一是他把物理问题表述为线性偏微分方程的边值问题来处理。这一点，连同他在单位和量纲方面的工作，使分析力学超出了牛顿在《自然哲学的数学原理》中所规定的范畴。二是由他所发明的解方程的强有力的数学工具产生了一系列派生学科，在数学分析中提出了许多研究课题，极大地推动了19世纪及以后的数学领域中的第一流的工作，并且开拓出一些新的领域。况且，傅立叶的理论和方法几乎渗透到近代物理的所有部门。

傅立叶在《热的解析理论》这部著作中，写进了他的差不多所有有关的工作，而且在此书的各个版本中几乎丝毫未加更动。因此，把这些内容联系其他没有发表的、为人引述的、散见于各处的资料，贯串起来，就可以切实地概现他的全部研究成果，以及他表述和处理问题的风格。同时，通过这些材料，也可以看出，在某些关键之处，傅立叶未能克服的困难和他失败的原因。

傅立叶在热的分析理论方面的第一件工作中，采用了这样的模型：热是由分立粒子间的穿梭机制传送的，其物理理论是简单的混合过程，所用数学属于18世纪50年代的。在他所研究的问题中，其一是关于排列在一圆环上的n个粒子。他获得在n为有限数的情形下的完全解。他想把结果推广到连续的情形未能成功，因为当n无限增大时，指数上的时间常数趋于零，从而使所得的解与时间无关。后来他才明白应如何修正他的传输模型以避免这一反常的结果。此外，在他集中注意于完全解及其困难时，他未能意识到，当t＝0时，他的解给出一个内推公式，可用以得到连续情形下的傅氏级数。（拉格朗日此前之所以未能发现傅氏级数也可类似地来解释，而并非像通常所认为的那样，是由于顾虑到严格性所致。）

傅立叶成功建立的热传导方程可能是得益于毕奥（J. B. Biot, 1774—1862）早先关于金属条中的稳定温度的工作，毕奥区分了体内传导和体外辐射。但是毕奥的分析，由于用了一个错误的物理导热模型而导出一不正确的方程。傅立叶则因构建了较好的物理模型而克服其困难，容易地获得一、二维情况下充分显示与时间的关系的类似于（1）这一类型的方程。

傅立叶的杰作是选择这样一种情形的问题来应用他的方程的，即一条半无穷的带，一端是较热的均匀温度，沿其边则是较冷的均匀温度，具有极其简单的、导源于伯努利兄弟（Bernoullis）和欧拉（L. Euler, 1707—1783）的分析力学传统中的物理意义。稳定情形无非就是笛卡儿坐标下的拉普拉斯方程。傅立叶可能试用过复变函数方法（这样的解见于他的《热的解析理论》一书中）。但其后就用分离变数法得到了级数解和以下边界条件的方程：

用无穷矩阵的方法来求方程（4）的解，并将它推广到任意函数f（x），这一工作曾屡次遭受批评。但不应忘记，这一工作是在柯西—魏尔斯特拉斯（Cauchy-Weierstrass）的正统理论建立之前几十年做的。傅立叶不是一个头脑简单的形式主义者；他精于处理有关“收敛”的问题，在他讨论锯齿形函数的级数表示时就显示出了这种能力。有关傅立叶级数的收敛性的几种基本证明，例如狄利克雷的证明，其主要思想均可在傅立叶的著作中找到。而且，比任何人更早，他已看到，在计算傅氏级数的系数时，对一给定的三角级数逐项积分，是不能保证其正确性的。

傅立叶的三角级数展开的使人震惊之处在于，他表明一种似乎是予盾的性质：在一有限区间内，完全不同的代数式之间的相等性。对于很广泛的一类函数中的任何一个函数，都可以相应地造出一个三角级数，它在指定的区间内具有与这函数相同的值。他举例说明，那给定的函数甚至可以在基本区间内分段有不同的代数表示式。虽然三角级数展开和任意函数两者曾为其他人（包括泊松）用过，但前者只限于有关周期现象的问题，而后者，当作为偏微分方程的解出现时，由于其性质，是假定不可能用代数式表示的。

关于傅立叶这一首次成功的研究结果的早期记载，说明了这个结果的生命力和他本人对此成果的惊异。在他的工作中，有受到蒙日影响的痕迹，如用曲面表示解，以及确定方程的解的边界值的分离表示。此后，傅立叶满怀信心地进入了新的领域。在三维情形遭到了一些困难，但把原方程分为两个方程就解决了。这两个方程，一个与内部传导有关，一个则与表面上的温度梯度所产生的辐射有关。应用于球体时运用球坐标，结果是一非谐的三角级数展开，其中的本征值是一超越方程的诸根。傅立叶运用他关于方程式论的知识，论证了这些根的实数性。当然，这一问题曾使他困惑了多年。在圆柱体的热传导问题中他又作了进一步的推广，其傅立叶解就是如今所称的贝塞尔（Bessel）函数。所用的技巧由傅立叶后来的同事佛朗索（J. C. François）、斯特姆和刘维（J. Liouville, 1809—1882）全面地予以普遍化。

在研究沿一条无穷长的线上的热传导问题时发展出来的傅立叶积分理论，可能是基于拉普拉斯把热扩散方程的解表示为一任意函数的积分变换的思想，这函数表示初始的温度分布。傅立叶通过对有限区间中级数展开的推广，分别导出了对原点是对称的和反对称的情形之下的余弦和正弦变换。逐渐地他才认识到，把一给定的函数分解为偶函数和奇函数的普遍性。

傅立叶在这方面的创造性工作于1817—1818年间又最后一次绽发光辉，他成功地洞察到积分变换解与运算微积之间的关系。当时，傅立叶、泊松、柯西（A. L. Cauchy, 1789—1857）之间形成了三足鼎立之争。后两人于1815年已开始运用这样的技巧，但是傅立叶针对泊松的批评给予了摧毁性的反击。他展示了几个方程的积分变换解，这几个方程是长期以来未能得到分析的，同时他还提出了导致系统理论之门径。其后，柯西运用复变函数中的残数（residue）理论也获得了同样的结果。

作为一位数学家，傅立叶对于实际问题中的严格性的关心，不亚于除柯西和阿贝尔以外的任何人，但他未能想到极限理论本身的重要意义。在对他1811年获奖论文的评议中，关于缺乏严格性和普遍性的批评，长久以来是被误解了。那些批评，其动机有许多是带有政治成分的。泊松和毕奥，是在热扩散理论方面被他超过的劲敌，多年来总是力图贬低傅立叶的成就。关于严格性的批评，可能是根据泊松的观点，即认为在球形问题中出现的本征值未能证明是实数，而复数根将导致在物理上是不可能的解。（泊松自己在数年后为傅立叶解决了这一问题。）所谓傅立叶级数解（2）缺乏普遍性，可能是将它同拉普拉斯早先得到的积分解对比，而在后者中，被积函数清楚地含有任意函数。

傅立叶的机智在于分析力学方面。他对分析技巧和符号表示极为精通，例如，定积分符号 就是他发明的。这种能力，加上他的物理直观力，使他的研究能够获得成功。在他之前，分析力学中出现的主要方程常是非线性的，所用解法都是专设的近似法。当时，微分方程领域也像是一个尚无通路的丛林。傅立叶为解偏微分方程创造了和说明了一种连贯的方法，即可以把一个方程及其级数解按照不同的物理情况清楚地分离为不同的分部来加以分析。我国数学家、微分方程方面的专家申又枨教授（1901—1978）曾经说：“傅立叶的创造，是给各种类型的偏微分方程（波动方程、扩散方程、拉普拉斯方程等）提供了一种统一的求解方法，就好比从前在算术中解“四则问题”时各种难题有各种解法，而运用代数方程以后，就有了统一的简便的解法。”这个比喻，很好地形容出傅立叶的方法在微分方程领域的重要意义和广泛的实用价值。事实上，傅立叶的方法确实是如此之强有力，以致过了整整一个世纪，非线性微分方程才重新在数学物理学中突起。

对傅立叶来说，每一数学陈述（尽管不是形式论证中的每一中间阶段）都应有其物理含意，包括展示真实的运动和能够（至少原则上）被测量两个方面。他总是如是地说明他的解，使所得到的极限情况能为实验所检验，而且一有机会他就自己动手来做实验。

傅立叶早年草设的物理模型虽很粗糙，但在他1807年所写的文章里，就已全面地把一些物理常数糅进他的热传导理论中。对物理意义的关注，使他看到在他的形式技法中所存在的潜力，能检验在傅立叶积分解的指数上出现的成群的物理常数的相关性。由此出发，他得出了关于单位和量纲的全面理论，虽然其中一部分是L. 卡诺（Lazare Carnot, 1753—1823）曾预期到的。这是自伽利略以来在物理量的数学表示理论方面第一个有成效的进展。与他同时代的人，如毕奥，在同一问题上的混乱情形相比，就更显示出傅立叶的成就。

虽然傅立叶多年从事热的物理理论的研究，但是他最初基于热辐射现象方面的贡献却未能长久存在。他对他的理论的各种应用都很关心，诸如对温度计的作用和房间供暖问题的分析，以及最重要的，对地球年龄下限首次作出的科学的估算等。令人不解的是，傅立叶相信热作为宇宙中的首要媒介的重要性，但他似乎对于热作为一种动力方面的问题却不感兴趣，以致对S. 卡诺（Sadi Carnot, 1796—1832，是L. 卡诺的儿子）有关热动力问题的著名论文毫无所知。

和傅立叶的著名的热传导问题的成就相比，他在数学的其他方面的工作就鲜为人知了。首先是他对方程式论有着长时间的浓厚兴趣。早在16岁时他就作了关于笛卡儿在负号法则的一个新证明。这一法则可表述如下：

设f（x）＝x^m ＋a₁ x^m－1 ＋…＋a_m－1x ＋a_m ，则f（x）的诸系数具有一系列正负号。如果把同号的两相邻系数称为“不变”，异号的称为“变”，那么f（x）的正（或负）根的数目最多等于序列中“变”（或“不变”）的数目。

傅立叶的证明方法是这样的：以（x＋p）乘f（x），得一新的多项式，它比f（x）多了一个系数，使系数序列中多了一个正负号，同时多了一个正（或负）根p；并且可以看出系数序列中“变”（或“不变”）的数目至少增加1个。因为傅立叶的这一成果很快就成为标准的证法，所以证明的详情可见于任何一本讲述这一法则的代数教科书，虽然人们未曾知道这一证法的发明者就是青年傅立叶。

傅立叶还把笛卡儿法则推广到估计在一给定区间［a，b］内f（x）的实根数，并于1789年向科学院递交了一篇文章，其中有他对自己的定理的证明，可惜文章在巴黎那革命动荡的年代里丢失了。大约30年后这篇文章才得以发表。由于另有一位兼职数学家布当（Ferdinand Budan de Bois-Laurent）也发表过类似的结果，所以关于在给定区间内n次代数方程的实根数的判定法，后来被称为傅立叶—布当定理。直到傅立叶逝世之前，他始终没有中断过方程式论方面的研究，并且计划写出一部七卷本的专著：《方程判定之分析》（Analyse des équations déterminées）。他已写出头两卷，但他预感到生前大概不可能完成这部著作，于是写了一个全书提要。1830年，由他的友人纳维埃（Navier）将这部未完成的著作编辑出版。从全书提要中，可以看出傅立叶对方程式论有过十分广泛的研究。其中最重要的是各种区分实根和虚根的方法，对牛顿—拉夫逊（Raphson）求根近似法的改进，对D. 伯努利求循环级数中相继项之比的极限值的法则的推广，等等。由于傅立叶还有线性不等式的求解法和应用方面的工作，以及他对这一问题的出众的理解，因而也被后人称为线性规划的先驱。

在傅立叶的最后的岁月里，当他主持统计局的工作时，他的研究接触到概率和误差问题。他写下了一些关于根据大量观测来估计测量误差的重要文章，发表于1826年和1829年的统计局报告上。傅立叶对力学问题也作过相当多的探讨，他曾发表过关于虚功原理的文章。

对科学和哲学的深远影响

综观傅立叶一生的学术成就，他最突出的贡献就是他对热传导问题的研究和新的普遍性数学方法的创造，这就为数学物理学的前进开辟了广阔的道路，极大地推动了应用数学的发展，从而也有力地推动了物理学的发展。

傅立叶大胆地断言：“任意”函数（实际上是在有限区间上只有有限个间断点的函数）都可以展成三角级数，并且列举大量函数和运用图形来说明函数的三角级数展开的普遍性，虽然他没有给出明确的条件和严格的证明，但是毕竟由此开创出“傅立叶分析”这一重要的数学分支，拓广了传统的函数概念。1837年，狄利克雷正是研究了傅立叶级数理论之后才提出了现代数学中通用的函数定义。1854年，黎曼（G. F. B. Riemann, 1826—1866）在讨论傅立叶级数的文章中第一次阐述了现代数学通用的积分定义。1861年，魏尔斯特拉斯运用三角级数构造出处处连续而处处不可微的特殊函数。正是从傅立叶级数提出来的许多问题直接引导狄利克雷、黎曼、斯托克斯（G. G. Stokes, 1819—1908）以及从海涅（H. E. Heine, 1821—1881）直至康托尔（G. Cantor, 1845—1918）、勒贝格（H. L. Lebesque, 1875—1941）、里斯（F. Riesz, 1880—1956）和费希（E. Fisch）等人在实变分析的各个方面获得了卓越的研究成果，并且导致一些新的数学部门，如泛函分析，集合论等分支的建立。傅立叶的工作对纯数学的发展也产生了如此深远的影响，这是傅立叶本人及其同时代人都难以预料到的，而且，这种影响至今还在发展之中。

傅立叶之所以能取得富有如此深刻内容的成就，正如撰写傅立叶传记的两位作者所说，这只有赋有生动的想象力和具有适合其工作的清醒的数学哲学头脑的数学大师才能达到。傅立叶有哲学头脑，但他没有写出哲学著作。从傅立叶的著作中，我们看到：他坚信数学是解决实际问题的最卓越的工具，并且认为，“对自然界的深刻研究是数学最富饶的源泉”。这一见解是傅立叶一生从事学术研究的指导性观点，而且已经成为数学史上强调通过研究实际问题发展数学（包括应用数学和纯粹数学）的一派数学家的代表性格言。

傅立叶的研究成果又是表现数学美的典型，傅立叶级数犹同用数学语言谱写的一首长诗。著名物理学家麦克斯韦（J. C. Maxwell, 1831—1879）曾把《热的解析理论》称为“一首伟大的数学的诗”。W. 汤姆孙（W. Thomson或Lord Kelvin, 1824—1907）不但称之为“数学的诗”，而且宣称他自己在数学物理中的全部生涯都受到了这部著作的影响。

傅立叶的研究工作还引起了他的同时代的哲学家的重视，法国哲学家、实证主义的创始人孔德（A. Comte, 1798—1857）在《实证哲学教程》（1842）中，把牛顿的力学理论和傅立叶的热传导理论都看做是实证主义基本观点在科学中的重要印证。而辩证唯物主义哲学家恩格斯（F. Engels, 1820—1895）则把傅立叶的数学成就与他所推崇的哲学家黑格尔的辩证法相提并论，他曾写道：“傅立叶是一首数学的诗，黑格尔是一首辩证法的诗。”

参考文献

1．J. Fourier, The Analytical Theory of Heat, translated with notes by Alexander Freeman, Dover Publication, Inc. 1955.

2．Fourier, Jean-Baptiste-Joseph, (written by J. R. Ravetz & I. Grattan-Guinness), in C. C. Gillispie, Dictionary of Scientific Biography, vol. V, Princeton University Press, 1972.3．H. S. Carslaw, Introduction to the Theory of Fourier Series and Integrals, Third Edition, New york, Dover Publication, 1950.

4．H. Eves, An Introduction to the History of Mathematics, Fourth Edition, Library of Congress Cataloguing in Publication Data, 1976.

5．M. Kline, Development of Mathematics in the 19^th Century, Chapter II, Math. Sci. Press, 1972.［德］K. 克莱因著《古今数学思想》，北京大学数学系数学史翻译组译，第2，3，4册，上海，上海科学技术出版社，1979。

6．E. T Bell, Men of Mathematics, New york, Dover Publication, 1963.

7．A. Zygmund, The Role of Fourier Series in the Development of Analysis, Historia Math. 2 (1975) No. 4.

8．王青建：“傅立叶——一位受人敬重的科学家”，《数学的实践与认识》，1988，No. 2。

9．恩格斯：《自然辩证法》，第183页，北京，人民出版社，1971。