第2章　论反射

解释了光波在均匀物质中传播的效应以后，下一步我们将考察当光波遇到其他物体时发生的现象。首先，我们将弄清楚，怎样用这些同样的光波来解释光的反射，以及为什么反射会保持角度相等。

惠更斯手稿中对钟摆观察的原始记录。

解释了光波在均匀物质中传播的效应以后，下一步我们将考察当光波遇到其他物体时发生的现象。首先，我们将弄清楚，怎样用这些同样的光波来解释光的反射，以及为什么反射会保持角度相等。

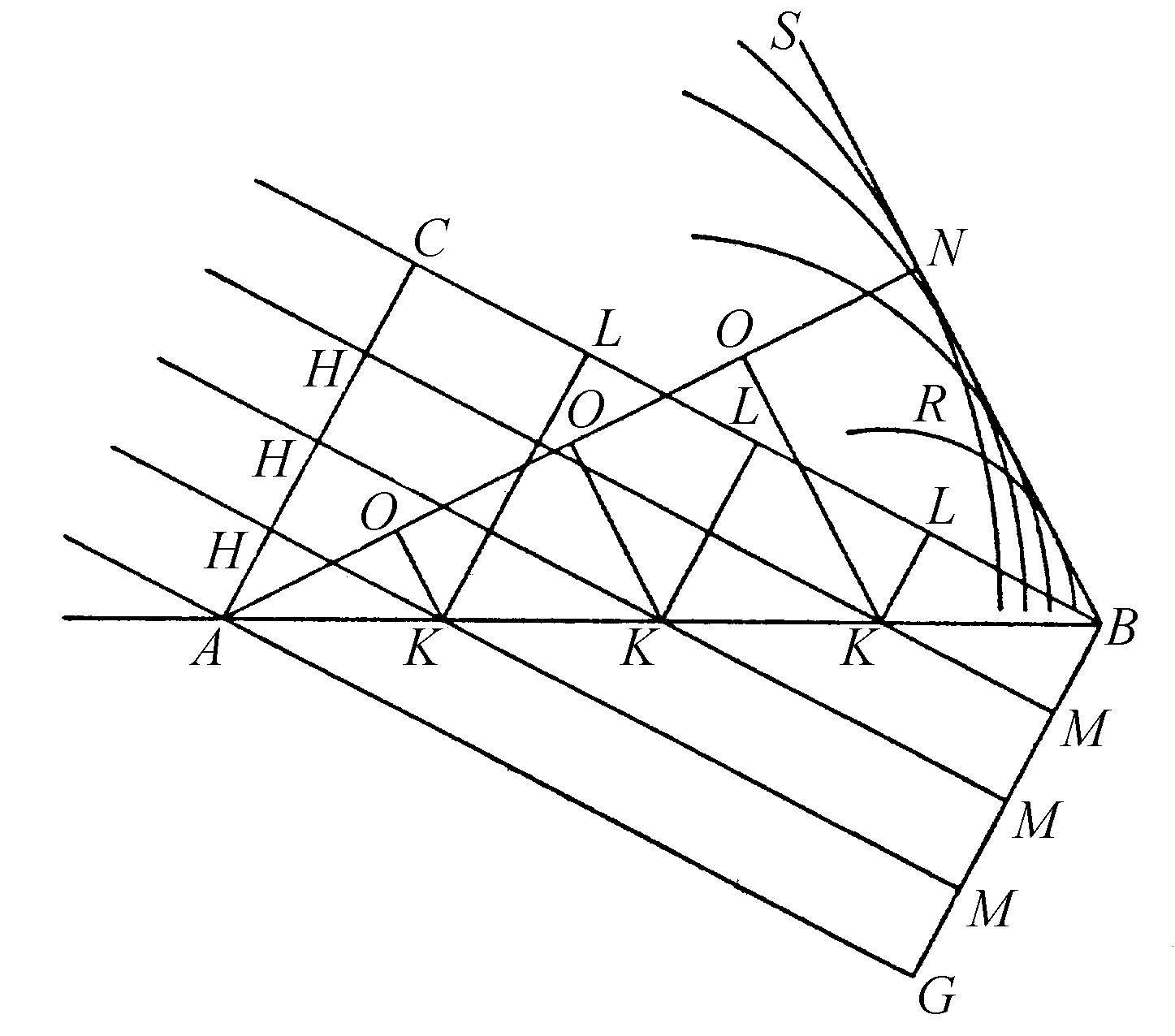图7

设有某种金属、玻璃或其他物体的一个表面AB，平滑而光亮（图7）。我先假定它是完全均匀的（我将一直使用这个假定，直到本章结尾处理一些不均匀问题止）。再设一条倾斜于AB的线AC，表示光波的一部分，而光波的中心离得非常远，以至AC可以被视为一条直线。由于我们好像在一个平面中来整个地考虑这个问题，设想本图所在的平面，是经过波的中心球面波的剖截面与AB平面正交。在整个讨论中只作这一次说明就够了。

波AC上的C点沿着直线CB，经过一段时间间隔行进到平面AB上的B点，可以假定CB从亮中心出发，并与AC垂直。在同样这段时间间隔内，同一个波上的A点，受到阻碍而不能或者至少部分地不能将其运动传播到AB平面以外，而不得不在该平面上方的物质中，沿着等于CB的距离继续运动，如前所述，发出它自身的球面分波。这个波在这里由圆周SNR表示，其中心为A点，半径AN与CB相等。

如果大家进一步考察波AC上的其他一些部分H，就可以看到，它们不仅沿着平行于CB的直线HK，到达了表面AB，而且还以K、K、K为中心在透明的空气中产生球面分波，这里用一些半径等于KM的圆周来表示，换句话说，这些半径等于HK延长到与AC平行的直线BG处的延长部分。显而易见，所有这些圆周有一个公切线BN，即从B点作出的那条直线，它与以A点为中心以等于BC的AN为半径的第一个圆相切。

直线BN（由B与过A的垂线的垂足N之间的点组成）本身是由所有这些圆周构成的，它限定由波AC的反射所引起的运动；而且在BN上发生的运动比其他任何地方都强得多。所以，依照前面的解释，BN是波上C部分到达B点时AC波的传播。因为除了平面AB下方的直线BG以外，再没有其他像BN那样的线，是上述所有圆的公切线；在这里假设了运动可以传递到与平面上方一样的介质中，直线BG是波AC的传播。如果你想要知道波AC是如何连续地传播到BN的话，你只需在上述图形中，画出平行于BN的直线KO，以及平行于AC的直线KL。这样你就看到平直波AC逐渐屈折为各个OKL部分，并在NB处再次变直。

这里很明显，反射角等于入射角。由于三角形ACB和BNA都是直角三角形并有一公共边AB，而且边CB又与边NA相等，则这些边对应的角相等，即角CBA等于角NAB。而且正像垂直于CA的CB标记入射线的方向那样，垂直于BN的AN标记了反射线的方向，因此，这些光线对于平面AB具有相同的倾角。

不过在考虑上述论证时，人们可能会认为，在本图的平面中BN为圆形波的公切线的确是真的，但是实际上作为球面波的这些波还有无数类似的公切线，即那些由直线BN经过B点绕轴BA旋转所产生的锥面上的直线。于是剩下的就是要证明在这个问题上并不存在什么困难，而且通过同样的论证，看到为什么入射线与反射线总是位于与反射平面垂直的同一个平面内。注意，被认为只是一条直线的波AC产生不了光。因为一束可见光线，不管它怎么窄，总有一个宽度。因此，表示波在行进时构成光线，有必要用某种平面图形来代替AC，就像我们已经采用的方法那样，通过假定光点在无穷远处，表示为图8中的圆HC。依照前面的论证容易看到，到达平面AB的这个波HC上的每一段都在AB上产生它的分波。在C到达B点时这些分波会有一个公切面，即一个类似于CH的圆BN，并且这个圆被一个平面从中间垂直地相交，该平面也与圆CH和椭圆AB同样地相交。

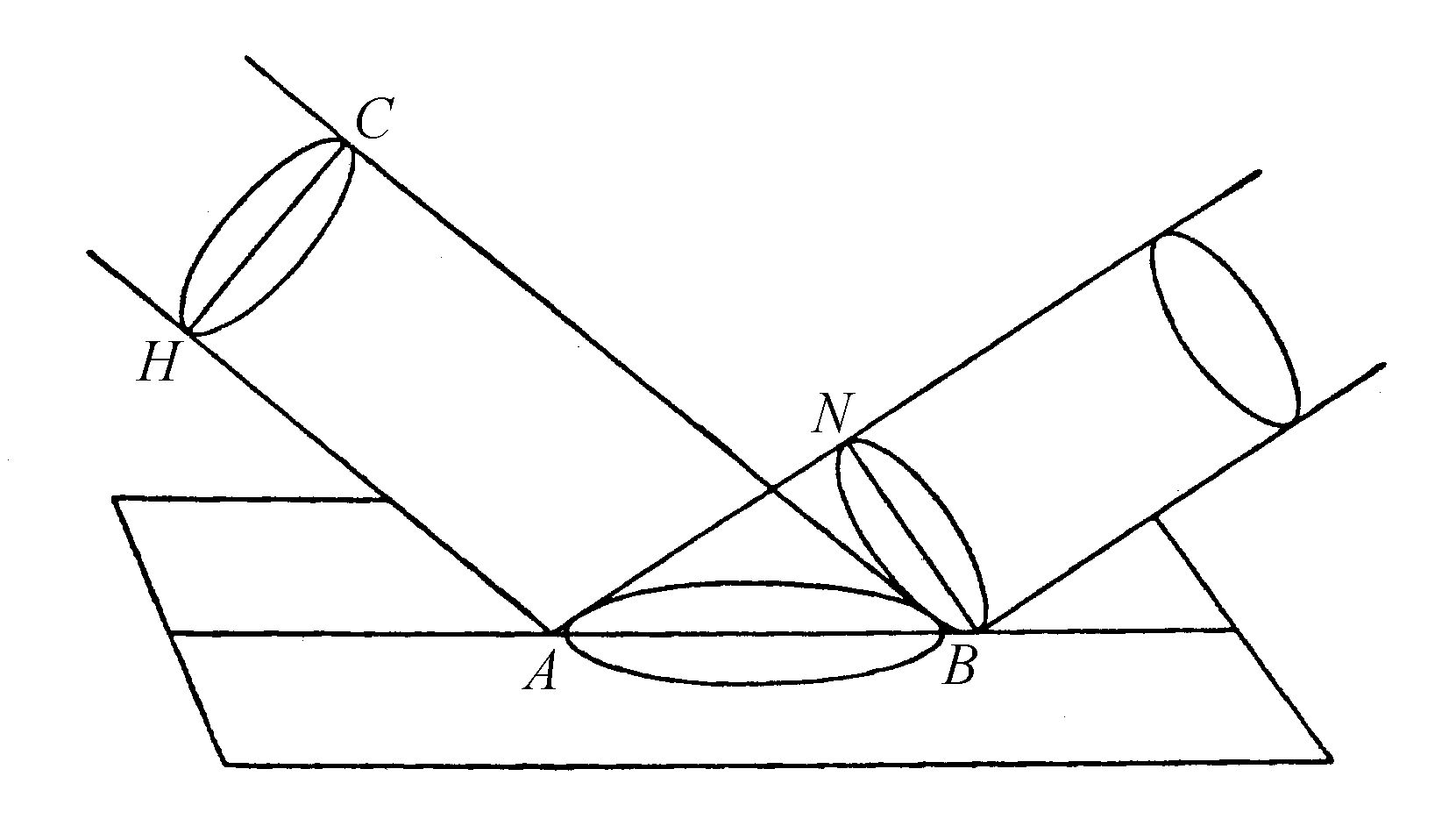图8

也可以看到，除了圆BN以外，所谓的分波球面不会再有其他的公切面；因此，正是在这一平面上，存在着比其他任何地方更多的反射运动，从而持续从波CH来的光。

在前面的论证中，我曾指出，入射波的A段的运动本身不能或者至少不能全部地传播到平面AB之外。因此必须注意，尽管“以太”物质的运动可能将其本身部分地传播到反射体，但这不能改变决定反射角的波的行进速度。因为在同一种物质中，轻微的撞击与强烈的撞击应当一样快地产生波。这一点出自我们以上所说过的像弹簧那样起作用的物体的性质，即无论压缩多少，它们反冲的时间相等。同样在光的一切反射中，对于任何物体，反射角总是应当等于入射角，不管该物体是否有一种可能吸收部分入射光运动的性质。并且实验表明，事实上没有哪一种磨光了的物体违背这个规律。

不过，在我们的论证中最值得提及的事情是，不像所有试图解释光效应的人们假设的那样，不要求把反射面考虑为一个均匀的平面；而只需要互相靠近放置的反射体的物质微粒所可能具有的那种光滑程度所得到的平面；这些微粒比“以太”物质的微粒要大些，关于这一点在我们讨论物体的透明性与蔽光性时还会涉及。由于反射面像这样由聚集在一起的微粒组成，而“以太”微粒在上面又比较小，显然不能以那些作者一贯采用的方法，类比球投向墙上时所发生的情况来证明反射角与入射角相等。但是在我们的方法中能毫无困难地作出解释。例如，由于应当设想在考虑的最小可见面中有无数微小的水银微粒，像一堆尽可能地撒平的沙粒那样排列着，就我们的情况而言，这个可见面就变得像擦亮的玻璃一样平。虽然与“以太”微粒比较起来，它始终是粗糙的，很明显我们所说的全部反射球面波的中心却几乎在一个均匀平面上，以至公切面能够按照光产生所需要的那样，精确地同它们吻合。在我们的论证方法中，只有这一点是必要的条件，不需要能引起相反作用的各处所反射的运动剩余部分，就使得所说的角度相等。