第七章　矩形棱柱中的热传导

·Chapter VII Propagation of Heat in A Rectangular Prism·

傅立叶比他同时代的许多人都更注意数学表述的物理意义。例如，把定积分看做面积就始于他，并且，通过对解中物理常数的关注，他得出了关于单位和量纲的完整理论，这是自伽利略以来在物理量的数学表示理论方面第一个有效的进展。

今日的巴黎高等师范学院微机械学大楼

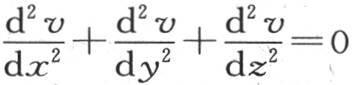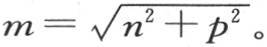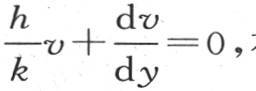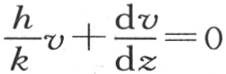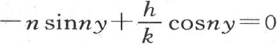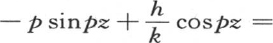
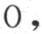321　我们在第二章第4节第125目中所陈述的方程 表示无穷长棱柱中的均匀热运动，该棱柱的一端受恒温作用，它的初始温度假定为0。为了对这个方程积分，我们首先研究v的一个特殊值，同时注意当y变号或者是z变号时函数v应当保持不变；并且当距离x无穷大时，它的值应当变得无穷小。由此不难看到，我们可以选择函数ae^-mx cosnycospy作为v的一个特殊值；作出这个代换，我们就得到m² －n² －p² ＝0。用任意两个量代替n和p我们都有 v的值在y＝l或-l时还应当满足定义方程 在z＝l或是-l时，满足方程 （第二章第4节第125目）。如果我们对v给定上述值，那么我们有 和 或者是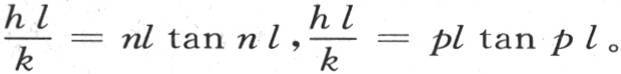 由此我们看到，如果我们找到一个弧ε，使得εtanε等于整个已知量 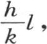那么我们就可以把量 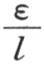看做是n或p。现在容易看到存在无数个弧，它们各自乘以它们的正切，就给出同一个确定的积 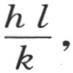由此得到，我们可以找到作为n和p的无数不同的值。

322　如果我们用ε₁ ，ε₂ ，ε₃ ，…表示满足定义方程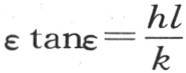 的无数个弧，那么我们可以用任一个这样的弧除以l来表示n。量p亦可以这样来表示；这时我们应当取m² ＝n² ＋p² 。如果我们对n和p给定其他的值，那么我们会满足这个微分方程，但是与表面条件无关。所以，我们可以用这种方法得到v的无数个特殊值，并且当这些值的任一集合的和仍然满足这个方程时，我们就可以建立一个更一般的v值。

依次对n和p取所有可能的值，即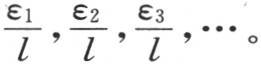 用a₁ ，a₂ ，a₃ ，…，b₁ ，b₂ ，b₃ ，…表示常系数，则v的值可以用下述方程来表示：

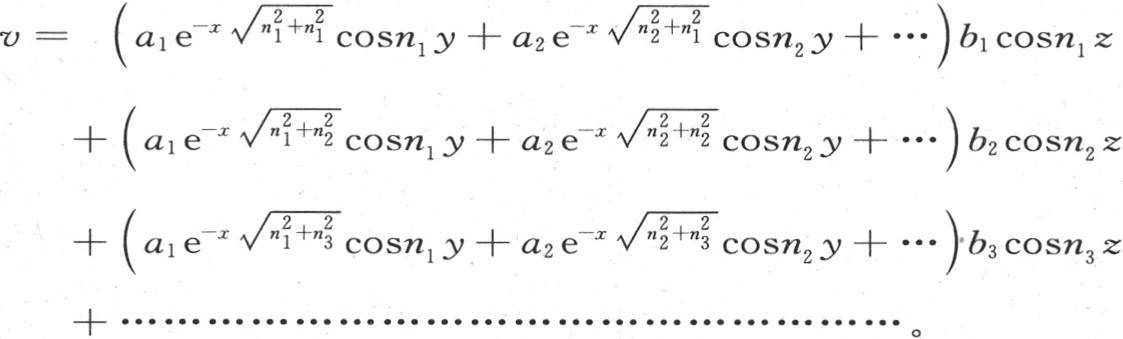
323　如果我们现在假定距离x为0，那么截面A的每一点应当保持一恒温不变。因此，一旦令x＝0，无论我们可能对y或者是z给定什么值，只要它们在0到l之间，v的值就必然总是一样的。这样，只要令x＝0，我们就得到v＝（a₁ cosn₁ y＋a₂ cosn₂ y＋a₃ cosn₃ y＋…）×（b₁ cosn₁ z＋b₂ cosn₂ z＋b₃ cosn₃ z＋…）。

用1来表示端面A的恒定温度，则出现两个方程1＝a₁ cosn₁ y＋a₂ cosn₂ y＋a₃ cosn₃ y＋…，1＝b₁ cosn₁ z＋b₂ cosn₂ z＋b₃ cosn₃ z＋…。这时，只要确定数目无穷的系数a₁ ，a₂ ，a₃ ，…，使得方程右边总可以等于1就够了。这个问题在数n₁ ，n₂ ，n₃ ，…形成奇数级数的情况下已经得到解决（第三章第2节第177目）。此处n₁ ，n₂ ，n₃ ，…是由无穷高阶方程所给定的一些不可通约量。

324　记方程1＝a₁ cosn₁ y＋a₂ cosn₂ y＋a₃ cosn₃ y＋…，用cosn₁ ydy乘方程两边，并从y＝0到y＝l取积分。因此我们确定第一个系数a₁ 。其余的系数可以以同一方法确定。

一般地，如果我们用cosνy乘方程两边，并对它积分，那么对应于右边由a cosny所表示的唯一的项，我们有积分a∫cosnycosνy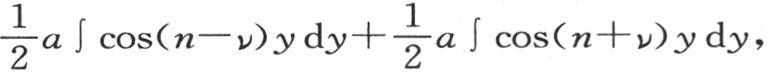或者是 或者是

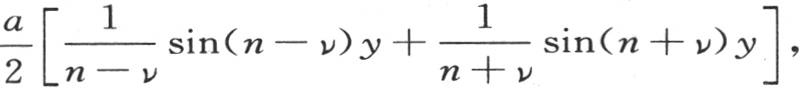
使y＝l，则有

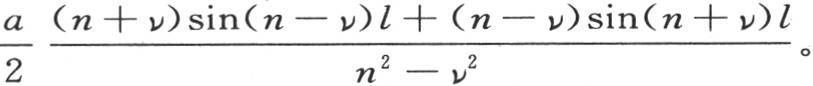
现在，n的每个值都满足方程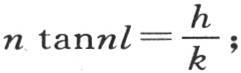 ν也如此，因此我们有n tannl＝νtanνl；或n sinnl cosνl－νsinνl cosnl＝0。所以，前面那个简化成 的积分，除开n＝ν这种唯一情况外，等于0。这时取积分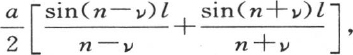 我们看到，如果我们有n＝ν，那么它等于量 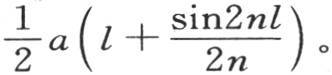由此得到，如果在方程1＝a₁ cosn₁ y＋a₂ cosn₂ y＋a₃ cosn₃ y＋…中，我们希望确定右边用a cosny所表示的某项的系数，那么我们就应当用cosny dy乘两边，并且从y＝0到y＝l积分。我们有合成方程 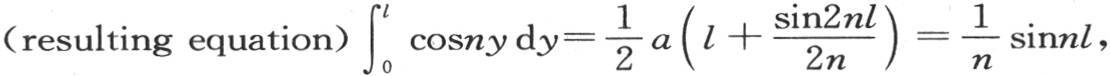由此我们推出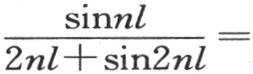 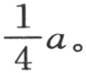如此，就可以确定系数a₁ ，a₂ ，a₃ ，…；b₁ ，b₂ ，b₃ ，…亦如此，它们分别与前面的系数相同。

325　现在不难建立v的一般值。

第一，它满足方程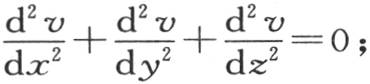

第二，它满足两个条件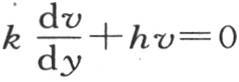 和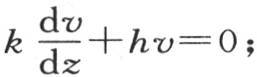

第三，当我们令x＝0时，在0到l之间，无论y值和z值是怎样的，它都给出v的一个常数值；因此，它是所提出的问题的全解。

我们因而得到方程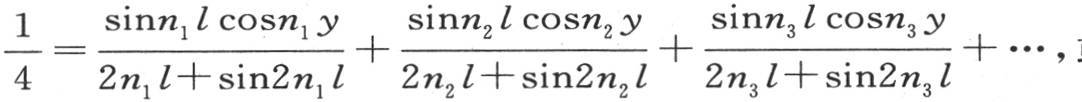 或者用ε₁ ，ε₂ ，ε₃ ，…表示弧n₁ l，n₂ l，n₃ l，…，则是 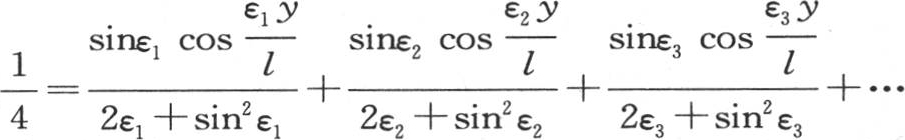， ^【1】 当x＝0时，这是对包含在0到l之间的所有y值都成立、因而对包含在0到-l之间的所有y值也成立的一个方程。

把a₁ ，b₁ ，a₂ ，b₂ ，a₃ ，b₃ ，…这些已知值代入v的一般值中，我们有下述方程，它包含所提出的问题的解，

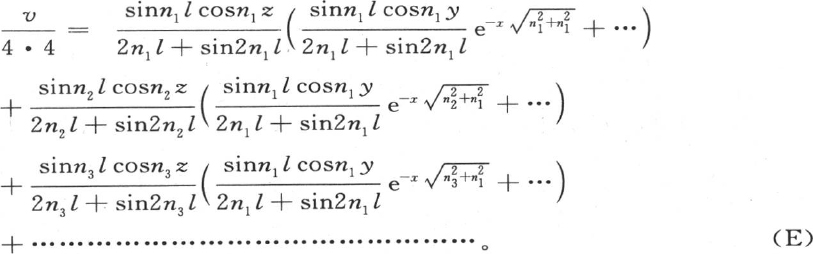
由n₁ ，n₂ ，n₃ ，…表示的量有无穷多个，并且分别等于量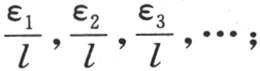 弧ε₁ ，ε₂ ，ε₃ ，…是定义方程 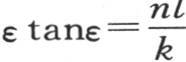的根。

326　由前面的方程（E）所表示的解是属于这个问题的唯一解；它代表方程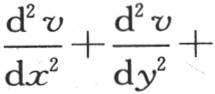 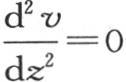的通解，其中，任意函数已随已知条件确定。容易看出，不可能有任何不同的解。事实上，让我们用ψ（x，y，z）表示从方程（E）所导出的v的值，显然，如果我们对这个固体给定由ψ（x，y，z）所表示的初始温度，那么只要在原点的截面保持恒温1，这个温度系统就不会发生任何变化：因为，由于方程 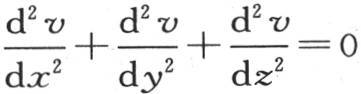被满足，所以温度的瞬时变化必然为0。如果在对这个固体内其坐标为x，y，z的每一点给定初始温度后，我们对在原点的截面给定温度0，那么情况则不同。无需计算我们就可以清楚地看到，在后一种情况下，固体的状态将不断变化，它所包含的初始热将一点一点地耗散到空气中去，并进入在末端保持0度的冷物质中去。这个结果依赖于函数ψ（x，y，z）的形式，当x有像这个问题所假定的一个无穷值时，这个函数的值变为0。

如果初始温度不是+ψ（x，y，z），而是在这个棱柱的所有内点为-ψ（x，y，z），则会存在类似的作用；只要在原点的截面总保持0度不变。在每一种情况下，初始温度都将不断趋近介质的恒定温度，这个温度为0；并且所有的终极温度都将是0。

327　在准备了这些预备步骤之后，考虑严格等于作为这个问题的对象的两个棱柱中的热运动。对于第一个固体，假定初始温度是+ψ（x，y，z），并且在原点A的那个截面保持固定温度1。对于第二个固体。假定初始温度是-ψ（x，y，z），在原点A的截面的所有点都保持0度。显然，在第一个棱柱中温度系统不可能发生变化，在第二个棱柱中这个系统则不断变化，直到所有温度都变成0为止。

如果我们现在让这两个不同的状态在同一固体中重合，那么热运动就会自由完成，就像每个系统都独立存在一样。在由这两个被联合起来的系统所形成的初始状态中，由假定，除截面A的点外，这个固体的每一点都是0度。现在第二个系统的温度变化愈来愈大，并且完全变成0，同时第一个系统的温度保持不变。因此，在无穷时间后，温度的永恒系统就变成由方程（E）或者是v＝ψ（x，y，z）所表示的系统。我们应当注意，这个结果依赖于和初始状态有关的条件；只要包含在棱柱中的初始热是这样分布的，就会出现若基底A保持0度不变则它完全变成0的情况。

328　我们可以对前面的这个解增加几个注记：

第一，不难看到方程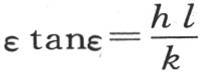 的性质；我们只需假定（见图15）我们已经作出曲线u＝εtanε，弧ε取作横轴，u取作纵轴。这条曲线由各渐近线的分支所组成。对应于渐近线的横坐标是 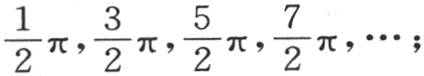对应于交点的横坐标是π，2π，3π，…。如果我们现在在原点作一个等于已知量 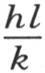的纵坐标，过它的端点作一条与横轴平行的平行线，那么交点就给出所提出的方程 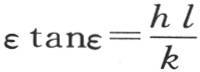的根。这个作图指明每个根所处的区间。我们不打算停下来指出应当用来确定这些根的值的运算过程。这类研究不存在任何困难。

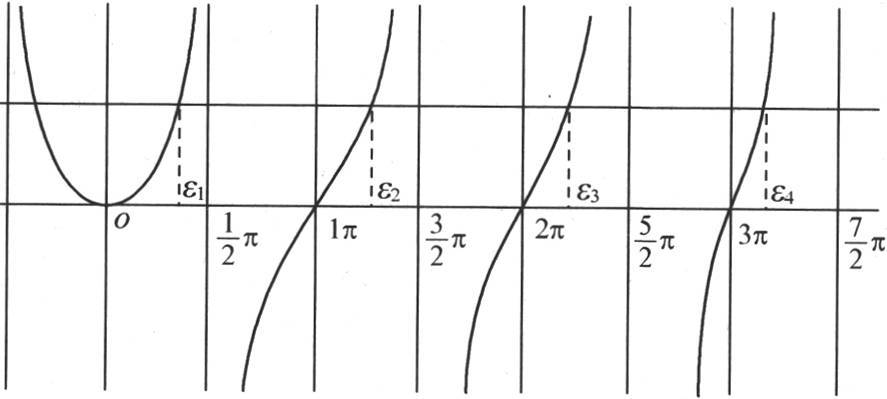
图15

329　第二，由一般方程（E）我们不难得到，x的值变得愈大，那么，在v值的各项中，我们能得到分数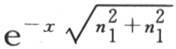 的那一项，相对于它后面的每一项来说，就愈大。事实上，由于n₁ ，n₂ ，n₃ ，…是递增的正数，所以分数 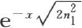大于进入后面各项的任一个类似的分数。

现在假定我们可以观察到在这个棱柱的轴上位于很远距离x处的一个点的温度，和这个轴上位于距离x＋1处的一点的温度，1是测量单位；这时我们有y＝0，z＝0，第二个点的温度与第一个的比明显等于分数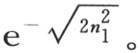 轴上这两点的温度比的这个值随距离x的增加而变得更精确。

由此得到，如果我们在这个轴上标出每个都与前一个的距离等于测量单位的点，那么某点与它前面一点的温度比，就不断收敛于分数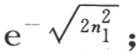 因此，距离相等的点的温度以按几何级数下降而结束。无论棒的厚度如何，只要我们考虑位置处在与热源相距很远的点，这个规律就总是成立。

由这个作图我们不难看到，如果所说的量l，棱柱厚度的一半，是很小的，那么n₁ 就取比n₂ ，n₃ ，…小得多的值；由此得到，第一个分数 比任何一个类似的分数都大得多。因此，在棒的厚度很小的情况下，为了使等距离的点的温度能以几何级数降低，与热源的距离就不必是很远的。这个规律在棒的整个范围内都成立。

330　如果半厚度l是一个很小的量，那么v的一般值就简化成含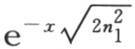 的第一项。因此，表示坐标为x，y，z的点的温度的函数v在这种情况下由方程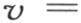 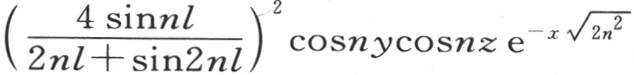所给出，弧ε或者是nl变得很小，正如我们由那个作图所看到的一样。这时方程 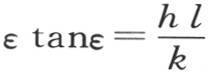简化成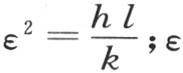 的第一个，或者说ε₁ 的值，就是 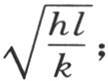通过对图形的观察，我们知道其他根的值，因而量ε₁ ，ε₂ ，ε₃ ，ε₄ ，ε₅ ，…依次是 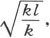π，2π，3π，4π，…。所以，n₁ ，n₂ ，n₃ ，n₄ ，n₅ ，…的值是 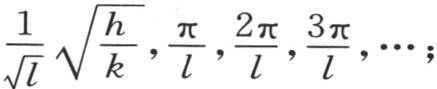由此得到，如我们上面所说，如果l是一个很小的量，那么第一个值n就比所有其他值无比地大，所以我们肯定可以从v的一般值中略去第一项之后的所有项，如果现在我们在第一项中代入所得到的n值，注意弧nl和2nl等于它们的正弦，那么我们有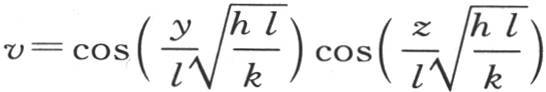 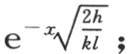由于进入余弦符号内的因子 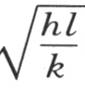很小，所以得到，当半厚度l很小时，对于同一截面的不同点，温度变化很小。这个结果可以说是自明的，但是注意到它怎样由分析来解释则是有用的。由于棒很细，这个通解事实上简化成唯一的一项，只要用1代替很小的弧的余弦，我们就有 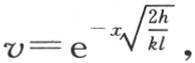在所研究的情况下表示驻温的一个方程。

在前面第76目中我们得到过同样的方程，在这里它是由完全不同的分析得到的。

331　前面的解指明这个固体内部的热运动的特征。不难看到，当棱柱在它的所有点都达到我们所考虑的驻温时，一股恒定热流就朝未受热的那一端流过垂直于轴的每一个截面。为了确定对应于一个横坐标x的热流量，我们应该设想在单位时间内流过这个截面元的热量等于系数k、面积dy dz、时间元dt和取负号的比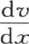 的积。因此，我们应该从z＝0到棒的厚度z＝l，从y＝0到y＝l，取积分 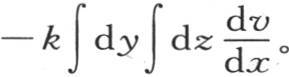这样我们得到整个热流量的四分之一。

这个计算结果揭示了流过棒的一个截面的热量如何减少的规律；并且我们看到，距离很远的部分从热源那里得到很少的热，因为它直接发出的热部分地朝表面耗散到空气中去了。通过这个棱柱任一截面的热，如果我们可以这样说的话，形成密度从这个截面的一点到另一点不等的一个热层。它通过处在该截面右边的这个棱柱的整个端面，对从表面逃走的热不断进行补充：由此得到，在一定时间内从棱柱的这一部分所逃逸的全部热量严格地由根据该固体的内热导率而进入的热所补偿。

为了检验这个结果，我们应当计算这一热流在表面所产生的热量。面积元是dx dy，v是它的温度，hv dx dy是在单位时间内从这个面积所逃逸的热量。因此积分h∫dx dy v表示从表面的一个有限部分所逃逸出去的总热量。假定z＝l，我们现在应当运用含y的v的已知值，然后一次从y＝0到y＝l积分，另一次从x＝x到x＝∞积分。这样我们得到从这个棱柱上表面所逃逸的热的一半；取这个结果的四倍，我们就得到整个上表面和下表面所失去的热量。如果我们现在使用表达式h∫dx∫dz v，对v中的y给定它的值l，并且一次从z＝0到z＝l积分，另一次从x＝0积到x＝∞；那么我们就得到从两个侧面所逃逸的热量的四分之一。

在所指明的界限之间，所取的积分h∫dx∫dy v，对于v的每一项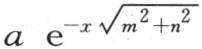 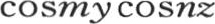， ^【2】 给出 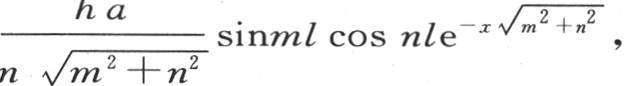积分h∫dx∫h z v给出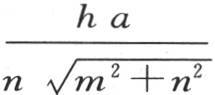

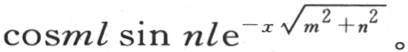
因此，这个棱柱通过位于横坐标为x的截面的右边的整个部分而从其表面所失去的热量，由类似于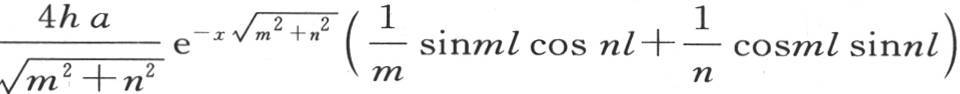 的所有项组成。另一方面，在同一时间内进入横坐标为x的这个截面的热量由类似于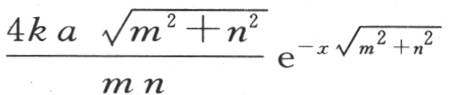 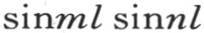的项组成；因此下述方程 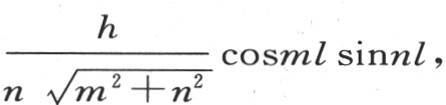或k（m² ＋n² ）sinml sin nl＝h m cosml sinnl＋h n sinml cosnl必然成立。现在我们分别有km² sinml sinnl＝h m cosml sinnl或者是 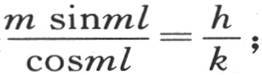我们也有kn² sinnl sinml＝hn cosnl sinml或者是 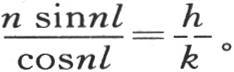因此该方程被满足。在被耗散的热和被传入的热之间不断建立的这种补偿是这个假定的一个明显结论；并且分析在这里再现已经表示过的条件；不过，注意在以前一直不服从于分析的新问题中的这种一致性是有用的。

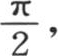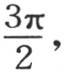332　假定作为棱柱基底正方形边长一半的l很长，并且我们希望确定轴的不同点的温度下降所遵循的规律；则我们应当在一般方程中对y和z给定为0的值，对l给定一个很大的值。现在作图在这种情况下表明，ε的第一个值是 第二个是 第三个是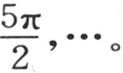 让我们在一般方程中作这些代换，并使n₁ l，n₂ l，n₃ l，n₄ l，…代之以它们的值 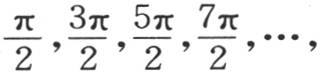同时用分数α代替 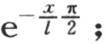这样我们得到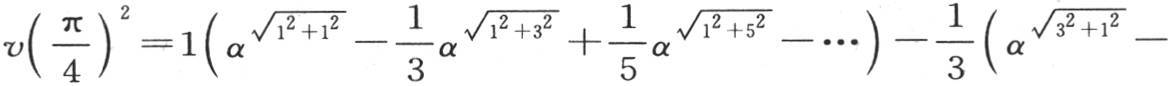

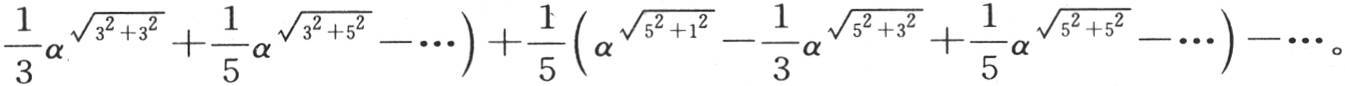
我们由这个结果看到，这个轴的不同点的温度随它们与原点距离的增加而迅速降低。如果这时我们在一个被加热并且保持永恒温度的支架上放一个无穷高的棱柱，该棱柱正方形基底的边长的一半l很大；那么热通过这个棱柱的内部而传导，并从表面耗散到周围的空气中去，周围空气的温度假定为0。当这个固体达到固定状态时，轴上各点将有极不相等的温度，在等于基底边长一半的高度上，最热一点的温度将小于基底温度的十五分之一。

注释

【1】 　在英译本中，此式分母中的正弦，分别是sinε₁ ，sinε₂ ，sinε₃ ，有误，现依法文《文集》本订正。——汉译者

【2】 　此式及其相应文字是根据法文《文集》本补充的。——汉译者