第2章　经典力学

引　　言

经典力学是当代理论物理学中最古老的部分，甚至可以说，现代科学就是从伽利略和牛顿对力学的表述开始的。西方文明中的一些最伟大的科学家如拉格朗日、哈密顿和庞加莱（Poincaré）等，都为经典力学作出过有决定意义的贡献。不仅如此，经典力学还是20世纪的科学革命如相对论和量子理论的起点。

不幸的是，多数的大学课本却把经典力学当做一门封闭的学科。我们将看到，经典力学并非一门封闭的学科，实际上，它是一门迅速进化着的学科。过去的20年间，科尔莫戈罗夫（Andrei Kolmogoroff）、阿诺德（Vladimir Arnol'd）、莫泽（Jürgen Moser）以及其他人介绍了一些重要的新发现，而在最近的将来，还可望有更重大的进展（Moser，1972）。

经典动力学已成为科学方法的范例。在法文中，人们常用“理性”力学这个词，意思是经典力学的定律正是理性的定律。经典动力学的属性之一是严格的决定论。在动力学中要基本上分清可任意给定的初始条件和用来计算系统以后（或以前）的动力学态的运动方程。如我们将要看到的那样，只有当一个完全确定的初始态的概念并不意味着过分理想化时，经典动力学的这个严格决定论的信念才是正确的。现代动力学是和开普勒的行星运动定律以及牛顿对“二体问题”的解一起诞生的。但是，只要我们一考虑第三个物体，比如说第二个行星，问题就变得惊人的复杂。只要系统足够复杂（例如在“三体问题”中），我们就会看到，关于系统初始状态的知识，无论具有怎样的有限精度，也无法使我们预言该系统在过了一段长时间后的行为。即使确定这个初始状态时精度变得任意大，这个预言的不确定性也还是存在。甚至从原则上也不可能知道，比如我们所居住的太阳系在整个未来是否稳定。这样的考虑极大地限制了轨道或世界线概念的可用性。所以，我们不得不去考虑和我们测量结果相容的那些世界线的系综（见图2.1）。但是，只要我们一离开对单个轨道的考虑，我们便离开了严格决定论的模型，我们就只能作出统计的预言，预报平均的结果。

图2.1　由与系统初始状态相对应的相空间中的一个有限区域发出的各种轨道

事情的变化往往是奇妙的。多年来，经典正统观念的支持者力图把统计的观点赶出量子力学（参见第3章）。爱因斯坦有一句名言：“上帝是不掷骰子的”。但我们现在看到，只要一考虑比较长的时间，就连经典动力学本身也需要统计的方法。还有更为重要的，那就是我们必须承认这样的事实：尽管经典动力学在一切理论科学中也许是最精致的，但它也不是一个所谓“封闭”的科学。我们可以对它提出一些有意义的问题，而它对此却给不出回答。

因为经典动力学在一切理论科学中是最古老的，所以它的发展在许多方面揭示了科学进化的内在动力。我们可以看到一些范例的产生、发展和衰亡。可积的动力学系统和遍历的动力学系统等概念就是这样的范例，我们将在本章的下面几节中叙述。当然，在本章里我们不能系统地叙述经典动力学的理论基础；只能着重提到和本书主题有直接关系的那些特性。

哈密顿运动方程和系综理论

在经典力学里，用坐标q₁ ，…，q_s 和动量p₁ ，…，p_s 来描述点粒子系统的状态较为便利。用上述变量表出的系统的能量，具有头等的重要性，它通常取如下形式：

其中第一项只取决于动量，是动能；而第二项只依赖于坐标，是势能（详见Goldstein，1950）。用这些变量所表达的能量就是哈密顿量，它在经典动力学中起着核心的作用。我们将只考虑所谓“保守系统”，即H不明显地依赖于时间的系统。一个简单的例子是一维谐振子，其哈密顿量是

其中m是质量，k是弹性常数，其值与谐振子的频率v（或角速度ω）有如下关系：

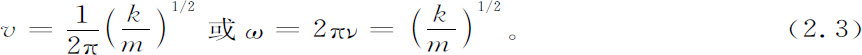
在多体系统中，势能通常是二体相互作用的总和，象在引力系统或静电系统中那样。

对我们来说，问题的要点是，只要知道了哈密顿量H，该系统的运动就决定了。的确，经典动力学的定律可以用下面的哈密顿方程来表达：

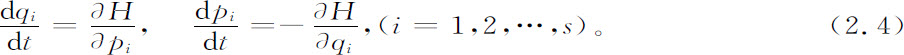
经典动力学能够用一个量——哈密顿量来表达自己的定律是它的一大成就。

现在，我们可以想象一个2s维的空间，其中的点由坐标q₁ ，…，p_s 确定。这个空间叫做相空间。每个力学态对应着这个空间的一个点p_t 。有了在时间t₀ 时起始点p的位置，再加上哈密顿量，就完全决定了该系统的变化。

考虑q₁ ，…，p_s 的一个任意函数，利用哈密顿方程2.4，该函数对于时间的变化由下式给出

这里的［f，H］是所谓f与H的泊松括号。因此，f不变的条件是

显然，

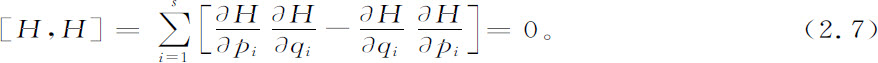
这个关系式简单地表示出能量的守恒。

为了实现动力学与热力学之间的连接，如吉布斯和爱因斯坦所作的那样，引入表象系综的概念是很有用的（Tolman，1938）。吉布斯对系综作了如下定义：“我们可以想象大量具有相同性质的系统，但它们在给定瞬时的组态和速度是不同的，而且这个不同还不仅是无穷小的。之所以如此，是为了体现各种组态和速度的一切可能的组合……”。

因此，基本的思想在于：我们考虑的不是一个单个的动力学系统，而是一个系统的集合，其中每一个系统都对应着同一个哈密顿量。这个集合或系综的选择，取决于加在系统上的条件（例如我们可以考虑孤立系统或者与热源接触的系统），同时也取决于对初始条件的了解程度。对于十分确定的初始条件，其相应的系综将很鲜明地集中于相空间的某个区域内；而对于不够确定的初始条件，则其相应的系综分布在相空间中一个很宽的区域上。

对于吉布斯和爱因斯坦来说，系综的观点不过只是一个方便的计算工具，以便在没有给出精确初始条件的情况下，用来计算平均值。但是，正如我们在本章及第7章中将看到的，系综观点的重要意义，比吉布斯和爱因斯坦当初所想象的要深远的多。

一个系统的吉布斯系综，在相空间中由一个“云”状的点集来代表（见图2.2）。

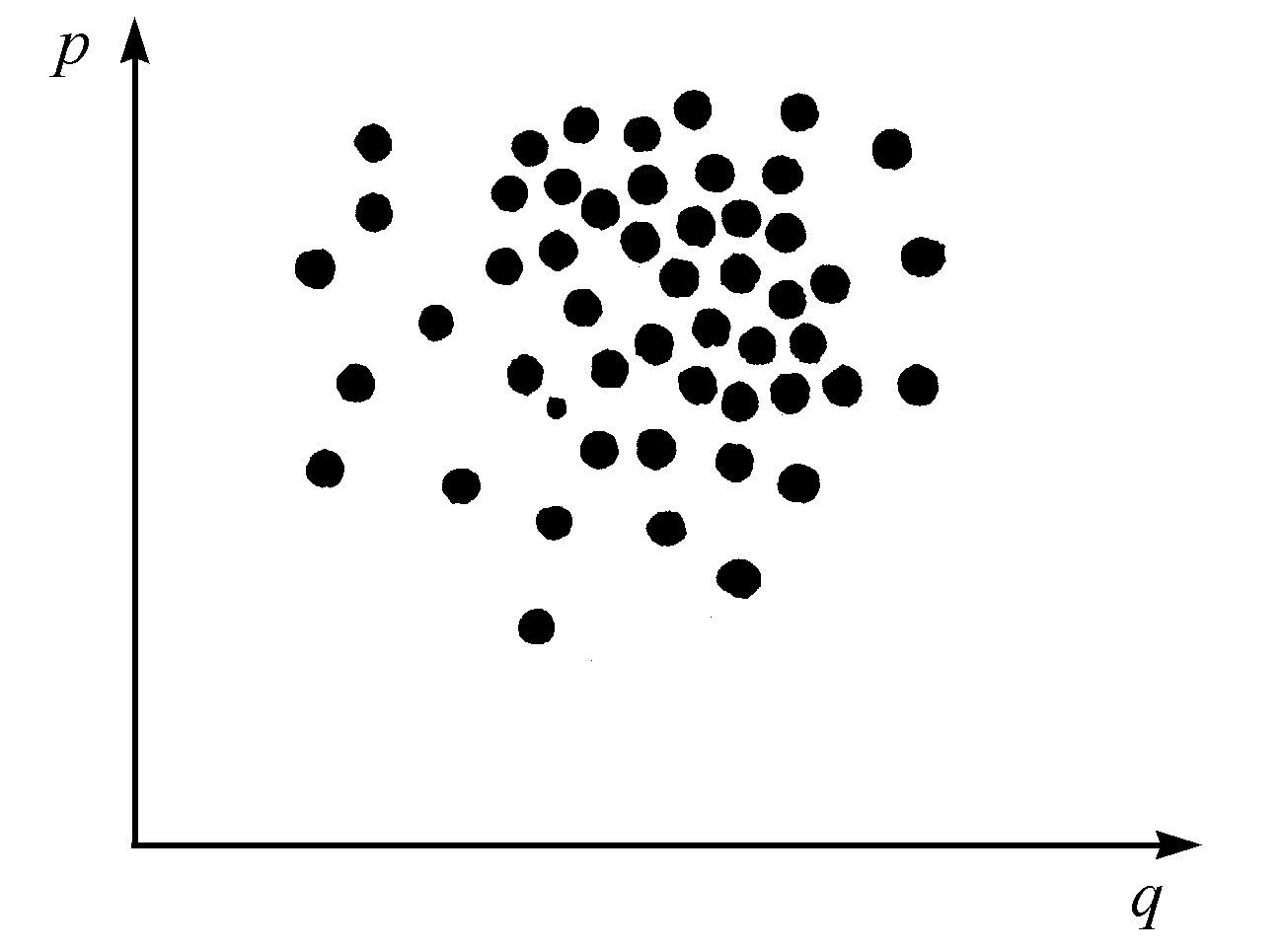
图2.2　吉布斯系综

这些系统（其状态由不同的点所描述）具有相同的哈密顿量和相同的约束，但它们的初始条件不同。

在每个区域都包含着大量点的极限情况下，这个“云”可以描述成连续的流体，它在相空间中的密度为：

因为系综中点的数目是任意的，所以我们可以把ρ归一化，就是

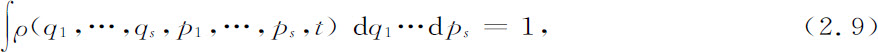
因此，

就代表了在时刻t，在相空间的体元dq₁ ，…，dp_s 中找到代表点的概率。

相空间的每个体元中密度的改变，是由于通过其边界的流动差。显著的特点是，相空间中的流动是“不可压缩”的。换句话说，流动的散度为零。的确，利用哈密顿方程2.4，我们有

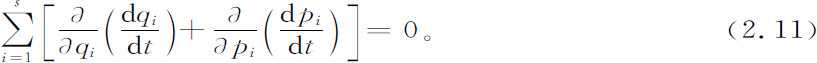
结果得到，相空间的体积对于时间是守恒的（见图2.3）。

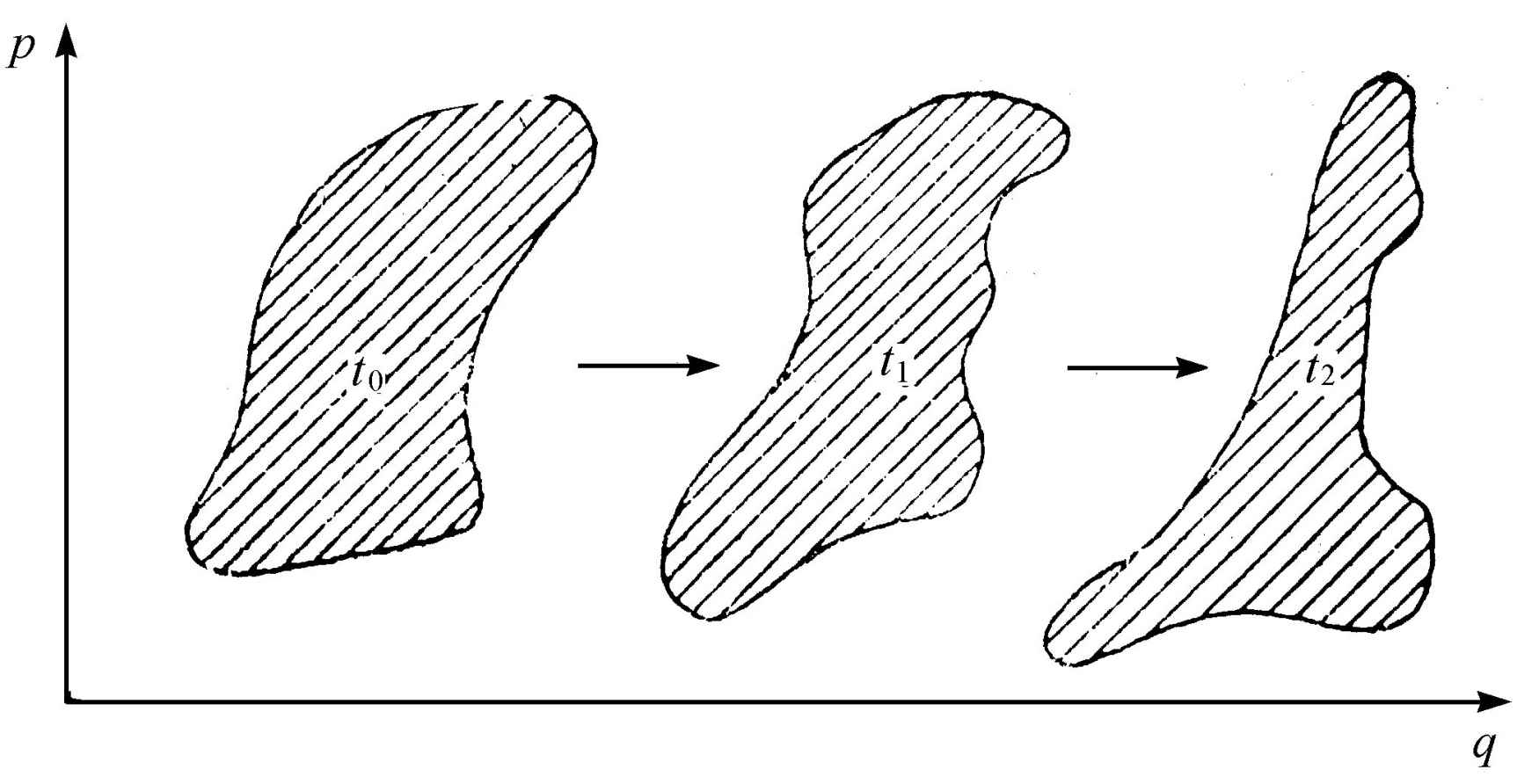
图2.3　相空间中体积的守恒

利用方程2.11我们得到一个对于相空间密度ρ的简单的运动方程。如所有教科书中所示（Tolman，1938），这就是著名的刘维方程，可写成如下形式：

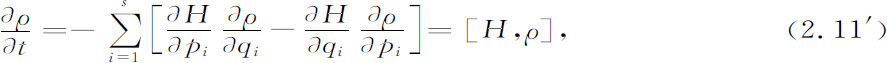
这里的括号，和方程2.5中的一样，是H与ρ的泊松括号。使用算符表述常常是很方便的，我们简单地用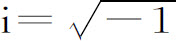 乘以方程（2.11′）并写作

这里的L就是线性算符：

下一节我们再详细讨论算符的概念。为了简化符号，我们只考虑一个自由度的情况。引入与i的乘积是为了把L作成一个厄米算符，如第3章中所研究的量子力学的许多算符那样。每本教科书里都有关于厄米算符的正式的定义；量子力学系统中算符的定义，我们将在第3章关于算符和并协性的一节里说明。它们之间的区别是，它们所作用的空间不同。经典力学中L作用于相空间，而量子力学中的算符是作用于“坐标”空间或动量空间的（见第3章）。近来，在统计力学中，刘维算符得到广泛的应用（Prigogine，1962）。

我们对系综理论的兴趣是显然的。即使我们不知道精确的初始条件，也可以考虑吉布斯密度，并利用系综平均的方法来计算任一力学性质A（p，q）的平均值

我们还要说明，很容易求出刘维方程（2.12）的如下的形式解：

这个表达式可以用直接求导的方法来验证，在这里提一句还是有必要的。吉布斯的系综方法，通过相空间的密度函数ρ，引入了概率的概念。用这个方法，我们既可以研究“纯”的情况，其中初始条件是事先给定的；也可以研究“混合”的情况，它相当于各种可能的初始条件。不过，密度函数的时间进化仍然具有严格决定论的动力学特色。它和概率过程或随机过程（比如第1章中叙述过的布朗运动）没有任何简单的联系。在这里，没有出现如转移概率那样的概念。一个最显著的差别是时间所起的作用。解2.12′对于所有的t值，无论正负，都是有效的；而解1.13却是仅对正t而言的。用数学语言说，解2.12′对应于一个群，解1.13对应于一个半群。

算　　符

一般地说，算符的引入是和量子力学有关的。我们将在第3章研究量子力学的观念。现在我们只强调，在采用系综观点时，经典动力学里也出现了算符。我们确实已在方程2.13中引入了刘维算符的概念。

算符通常具有本征函数和本征值。一个算符作用于它的某个本征函数时，得到的是这个函数乘以与之相应的本征值。例如算符A代表二阶导数：

显然，当它作用于一个任意函数（比如说x² ）时，它将把这个函数变成另一个函数。但是有些函数却保持不变，例如考虑“本征值问题”

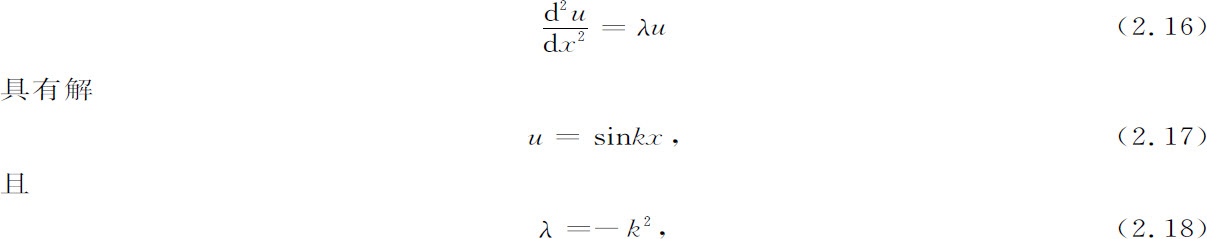
其中k为一实数。这些就是分别与该算符对应的本征函数和本征值。

本征值既可以是分立的，也可以是连续的。为了理解这个区别，我们再考虑本征值问题2.16。到目前为止我们还没有引入边界条件，现在我们加上这样的条件，就是在对应于x＝0和x＝L的域的边界处，本征函数为零。这些就是边界条件，它们在量子力学中的出现是自然而然的，其物理意义是粒子陷于该域中。这些边界条件很容易得到满足。的确，由条件

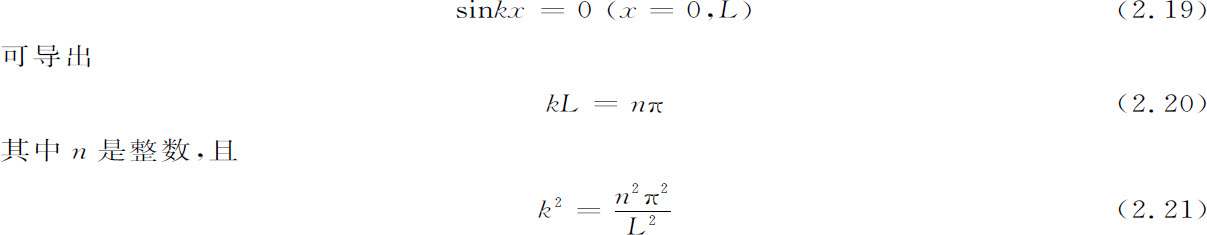
于是我们看到，两个允许态之间的间隔与域的大小有关。由于这个间隔与L² 成反比，所以在大系统的极限情况下，我们得到所谓连续谱。相反，在有限系统的情况下，我们得到分立谱。

常常需要考虑一个稍复杂的极限，其中系统的体积V和粒子数N都趋于无穷，但它们的比却保持为常数，即

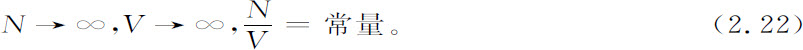
这就是所谓热力学极限，它在对多体系统的热力学行为的研究中起着重要作用。

区别分立谱和连续谱，这对描述相空间密度ρ的时间进化来说，是十分重要的。如果L具有分立谱，则刘维方程2.11′将导致周期运动。但是，如果L具有连续谱，运动的性质就会发生剧烈的变化。

我们将在第3章关于不稳定粒子衰变的一节回到这个问题上来。不过此处我们要注意：与量子力学中发生的现象相反，即使是一个有限的经典系统，也会具有连续谱。

平衡系综

我们在第1章中已经看到，趋近热力学平衡态，就是向一个终态的进化。对于初始条件来说，终态的作用就像是个吸引中心。不难猜想，用相空间中的吉布斯分布函数来说，这意味着什么。让我们考虑一个系综，它的所有成员都具有相同的能量E。吉布斯密度仅在由

所定义的能量面上不为零。

最初，我们自然会考虑这个能量面上的一个任意的分布。于是，这个分布就会按照刘维方程随时间而进化。关于热力学平衡态意味着什么这个问题，最简单的看法就是假定：在热力学平衡态，能量面上的分布ρ会趋向于一个常数。这就是吉布斯的基本思想，相应的分布被他称为微正则系综（Gibbs，1902）.吉布斯可以证明，这个假设导出了平衡态热力学的定律（亦见第4章）。除了微正则系综外，他还引入了别的系综，比如正则系综，对应于和一个在均匀温度T下的大能源接触的系统。这个系综也得出了平衡态热力学的定律，并能使人们对于像平衡熵这样的热力学性质，作出非常简单的分子解释。但是这里我们不再细谈这些问题了，而是把注意力集中于一个基本问题，必须给系统的动力学加上什么样的条件，才能保证分布函数趋向微正则的或正则的系综？

可积系统

在几乎整个19世纪内，可积系统的思想统治了经典动力学的发展（Goldstein，1950）。这个思想很容易通过谐振子的情况来说明。代替正则变量q和p，我们引入新变量J和α，其定义如下：

这个变换很像从笛卡儿坐标到极坐标的变换。α又叫角变量，J是相应的动量，称为作用变量（见图2.4）。利用这两个变量，方程2.2取简单的形式：

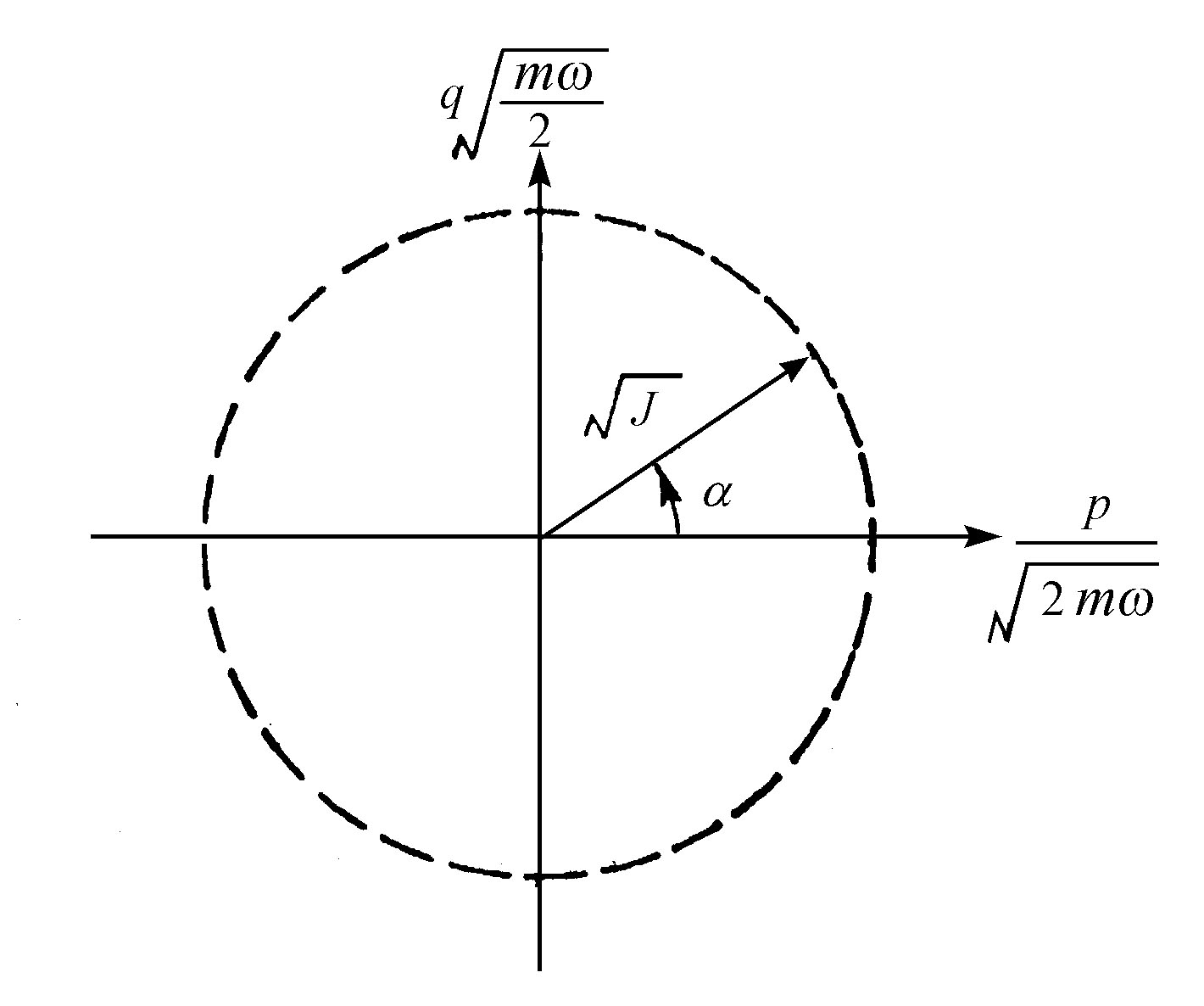
图2.4　谐振子从笛卡儿坐标p、q到作用变量J、角变量α的变换

我们实行了一个正则变换，它使哈密顿量从一种形式2.2变到了另一种形式2.25。我们得到了什么呢？在新的形式下，能量不再被分成动能和势能。方程2.25直接给出总能量。我们立即看到这个变换对更为复杂的问题所带来的好处。只要我们还有势能，我们就无法真正把一个能量赋予组成该系统的各个物体，因为有一部分能量是在各个物体“之间”的。通过这个正则变换，我们得到了一个新的表象，这个表象使我们可以谈到完全确定的物体或粒子，因为势能已被消掉。于是我们得到一个哈密顿量

而且它只和作用变量有关。对于一些系统，我们可以通过适当的变量代换，从方程2.1得到方程2.14以及从方程2.23得到方程2.26。按定义，这样的系统就是动力学的可积系统。于是，对于这些系统，我们可以如图2.5中所示的那样把势能“变换掉”。

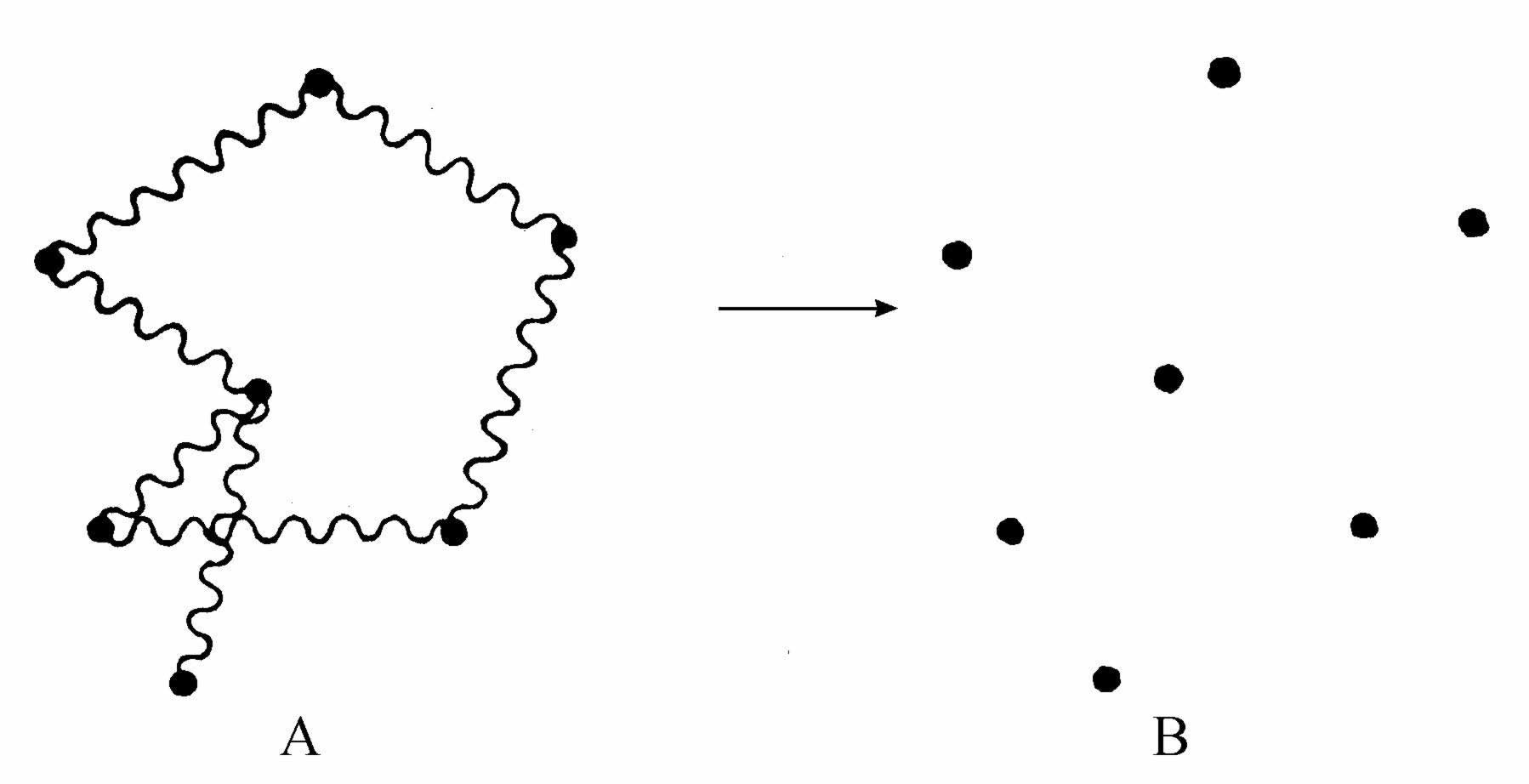
图2.5　可积系统势能的消失

在A中用波纹线代表势能。

物理世界，比如说由基本粒子及其相互作用所代表的物理世界，符合于一个可积系统吗？我们将在第3章回到这个基本问题上来。

到作用变量和角变量的变换，还有另一个显著特性，就是在方程2.25中，谐振子的频率ω可用哈密顿量直接表达出来（而不用通过运动方程的积分导出）。与之类似，在一般情况下，我们有s个频率ω₁ ，…，ω_s ，每个频率都通过

和哈密顿量发生关系。和作用变量J_i 对应的那些坐标，按定义就是角变量α₁ ，…，α_s 。物理量是这些角变量的周期函数。

用作用变量表达的形式为方程2.26的哈密顿量导致一些重要的结果。现在，正则方程是（见方程2.4和2.27）：

因此，每个作用变量是一个运动常数，而角变量是时间的线性函数。

在整个19世纪，研究经典动力学问题的数学家和物理学家都在寻找可积系统，因为一旦找到了变成哈密顿量形式的变换——方程2.26，积分问题（即运动方程的求解）就变得平庸了。因此，当布伦斯（Heinrich Bruns）首先证明（庞加莱又在更加一般的情况下证明），从包括太阳、地球、月球的三体问题开始，经典动力学中最令人感兴趣的问题并不能导致可积系统的时候（Poincaré，1889）科学界大为震惊。换句话说，我们不可能找到一个导致方程2.26形式的正则变换，因而也就不能借助于正则变换找到如作用变量J_i 那样的不变量。在某种意义上说，这乃是经典动力学整个前期发展的一个终点。

我们将在本章题为“既非可积又非遍历的动力学系统”的一节中讨论庞加莱的基本定理。让我们先简单提一下，从动力学与热力学的关系这个角度上看，庞加莱定理是最成功的。一般说来，假如有某些物理系统是属于可积系统这一类的，它们就不会忘掉它们的初始条件。假如开始时作用变量J₁ ，…，J_s 已具有给定的值，那么这些值就会一直保持下去，而分布函数就不会在与给定能量值E相应的微正则面上变得均匀起来。十分清楚，终态就会极大地依赖于系统的制备，而如趋于平衡这样的概念就会失去其意义了。

遍历系统

鉴于使用可积系统难于体现趋于平衡的问题，麦克斯韦和玻耳兹曼把注意力转向了另一类动力学系统。他们引入的学说，现在一般称为“遍历假说”。用麦克斯韦的话来说，“为直接证明热力学平衡问题所必需的唯一假定是，当系统处于实际的运动状态时，它将或迟或早地遍历满足能量方程的各个相点”。不过，一些数学家已经指出，一条轨道显然不能占满“一个面”，因此这个论点就不得不改变为，按照所谓“准遍历假说”，系统将或迟或早地遍历能量面上任意靠近的各个点（Farquhar，1964）。

值得注意的是，我们正在处理动力学系统的一个范例，它和在研究可积系统时所用的观点正好相反。在这个范例中，实质上只有一条“覆盖”着能量面的轨道。遍历系统只有一个不变量，而不是像可积系统那样，具有s个不变量J₁ ，J₂ ，…，J_s 。如果我们记得我们感兴趣的通常是多体系统，而对于这个多体系统来说，s具有阿伏伽德罗常数的数量级（约为10²³ ），就会发现差别确实是惊人的。

毫无疑问，存在着遍历的动力学系统，尽管它的类型是很简单的。作为遍历的时间进化的一个例子，我们可以给出在二维单位方格上的运动，相应的方程如下：

在周期边界条件

之下，这些方程很容易求解，因此，相轨道是

轨道的基本特点取决于α值。有两种情况必须分清：如果α是有理数，比方说α＝m/n，那么轨道就是周期性的，经过周期T＝n之后又重复，这样一来，系统就不是遍历的。另一方面，如果α是无理数，那么轨道将满足准遍历假说的条件。它就可以任意接近单位方格上的各个点。它将“填满”这个方格（图2.6）。

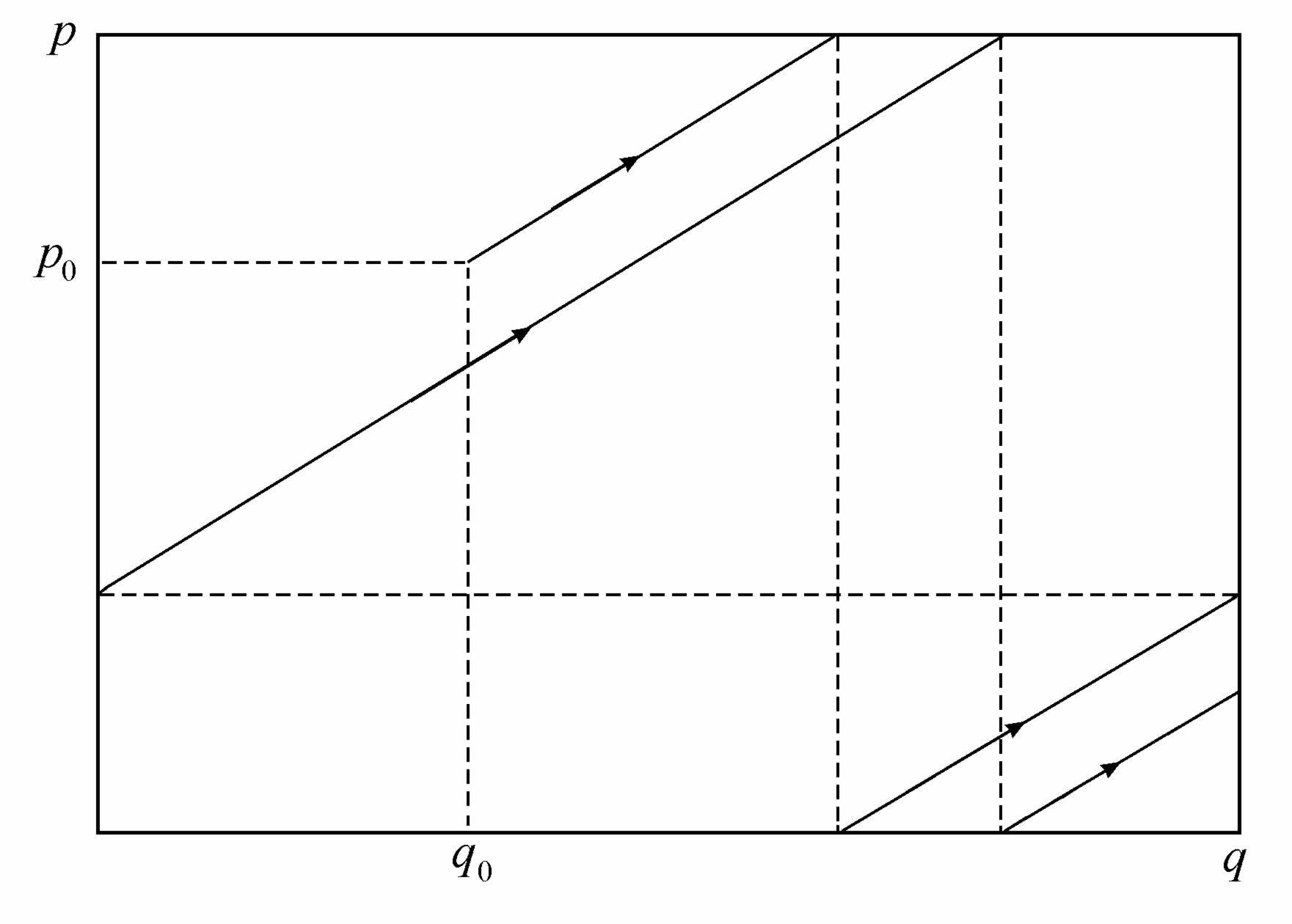
图2.6　方程2.31给出的相轨道

α是无理数时，轨道密集在单位方格上。

为以后参考起见，必须指出，尽管运动具有遍历性，相流体的每个小区域在运动中是没有形变的，因为小矩形Δp Δq不仅保持其大小，而且保持其形状。作为方程2.29的结果，有dΔp/dt＝dΔq/dt＝0。这和另一类运动是相反的（见第7章和附录A），在那里，相流体的运动引起强烈的扰动。

运动方程2.29中的数α和1是两个特征频率（ω₁ 和ω₂ ）；一个和p对应，另一个和q对应。可以写成

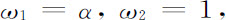
两个都是常数，这就是谐振子的频率，见方程2.25。

如果在一个动力学问题里含有一个以上的频率，那么有一个基本问题就是所谓频率的线性无关性。如果α是有理数，我们可以找到两个不全为零的数m₁ 和m₂ ，使得

因此这两个频率是线性相关的。另一方面，如果α是无理数，等式2.24对于非零的数m₁ 和m₂ 不可能成立，于是这两个频率就是线性无关的。

约在1930年，伯克霍夫（George Birkhoff）、冯·诺伊曼（Von Neumann）和霍普夫（Heinz Hopf）等人的工作对经典力学中的遍历问题给出了一个确定的数学形式（Farguhar，1964；Balescu，1975）。我们已看到，相空间中的流动是体积（或“测度”）守恒的。但是这仍留下多种未解决的可能性。在一个遍历系统的情况下，“相流体”扫过微正则面上的整个有效空间，但如所见，它可以基本上不用改变其形状而作到这一点。然而还有更复杂得多的流动也是可能的：即不但相流体扫过整个相体积，而且体元的初始形状发生严重的畸变。初始块向四面八方伸出变形虫式的手臂，这样就使得无论初始组态如何，分布总会在一段较长的时间之后变成均匀的。这种首先被霍普夫考查过的系统叫做混合系统（mixing system）。无法画出一个简单的图来表明这个流动，因为两个相邻的点无论多么靠近，也是会发散的。即使我们从一个形状简单的分布出发，最后我们得到的也是一个“怪物”。曼德布洛特就是这样正确地称呼具有这种复杂性的客体的（Mandelbrot，1977）。也许，和生物学的情形类比，可以阐明这个复杂性的程度：例如我们可以想一下肺叶以及它所包含的肺泡的多层组织多么复杂。

甚至还有比混合流动性质更强的流动，已被科尔莫戈罗夫和西奈（Ya. Sinai）特别加以研究（Balescu，1975）。使人特别感兴趣的是所谓“K流动”（K-flow），其特性更加接近随机系统的特性。

实际上，当我们从遍历流动进到混合流动，然后又进到K流动的时候，相空间中的运动就变得越来越不可预言了。我们也就越来越远离了决定论的思想，而这种思想在如此漫长的时间内一直是经典力学的特征（使用所谓面包师的变换的一个例子将在附录A中讨论。）

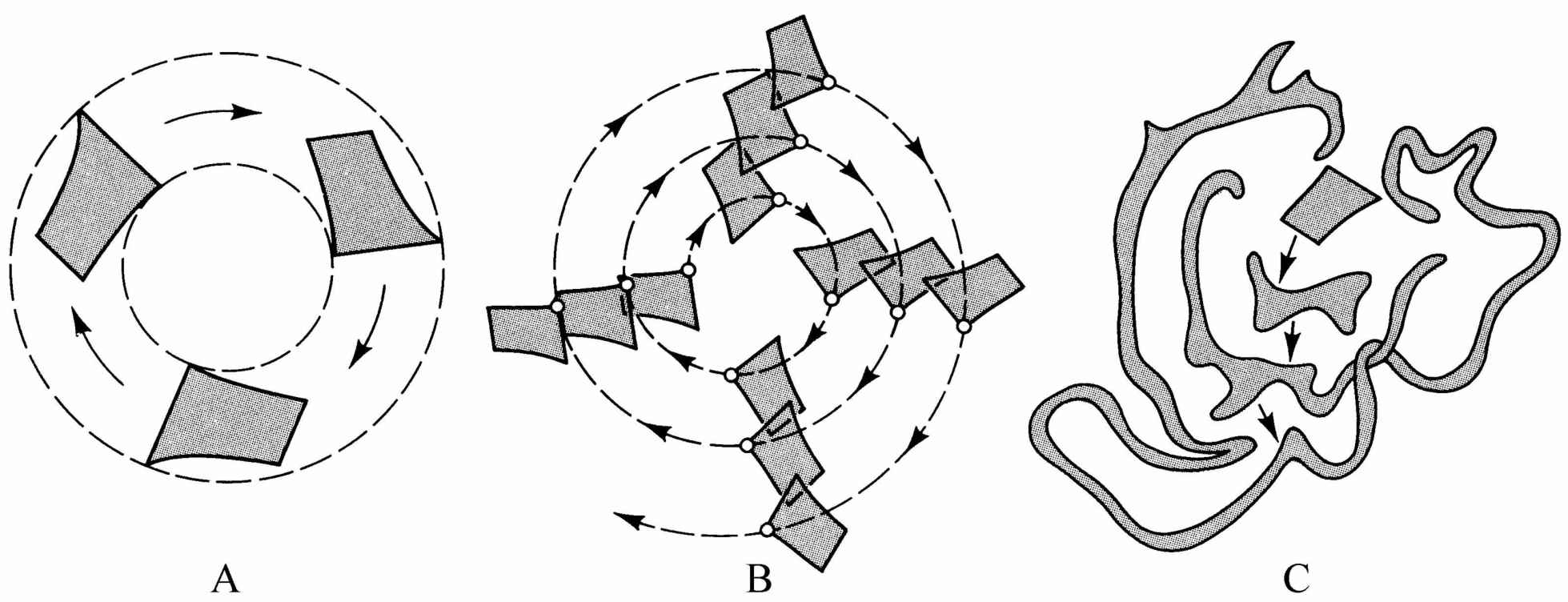
图2.7　相空间中各种类型的流动

（A）非遍历的；（B）遍历的但不是混合的；（C）混合的。

从L的谱特性来看，这些不同类型的流动之间的差别是十分简单的。比如，遍历系统意味着方程

有唯一的解，即

因此它对应于微正则面上的一个常数。

参照一下方程2.13，我们会看到方程2.34的确是方程2.33的解，但遍历系统的特点在于这个解是唯一的。同样（例如参见Lebowitz，1972），混合系统含有更强的性质，即L没有非零的分立本征值。最后，K流动意味着除了混合系统的性质外，其解的多重度（即对于给定本征值的解的个数）是常数。

遍历理论的一个意外的结果就是，运动的“不可预言性”或“随机性”与刘维算符L的如此简单的性质有关。在一系列值得注意的论文里，西奈（例如参见Balescu，1975）可以证明，一个盒子里有多于两个硬球的系统是一个K流动（因而也是混合系统和遍历系统）。可惜，不知道对于别的（特殊性更少一点的）相互作用定律，它是否仍能成立。不过绝大多数物理学家仍然持这样的观点，即认为这仅仅是形式上的困难，而且在物理系统里观察到的趋向平衡的现象的力学基础，一定能在遍历系统的理论中找到。

科尔莫戈罗夫在一篇重要的文章中首次提出了这样的看法：动力学系统一般地说应当是遍历系统（Kolmogoroff，1954）。他指出，对于多数种类的相互作用动力学系统，可以在限于遍历面上的一个子空间（不变环）内建立周期轨道。另一些研究也在减弱我们对遍历系统普遍性的信任。例如，一组重要的工作是由费米（Enrico Fermi）、帕斯塔（John Pasta）和乌拉姆（Stanislaw Ulam）实现的（Balescu，1975）。他们对非谐振子的耦合链的行为作了数字上的研究。他们预期这个系统应很快地达到热平衡态。然而他们发现的却是在各种简正模式的能量下的周期振荡。科尔莫戈罗夫的工作由阿诺德和莫泽发展成为所谓KAM理论。也许这个新理论的最使人感兴趣的方面就是：动力学系统可以导致随机运动，即有点类似在混合系统或K流动中发生的那种类型的运动，而并不取决于遍历性。让我们更详细地考虑一下这个重要的观点。

肺的模型

既非可积又非遍历的动力学系统

为了使我们对动力学系统的行为有一个清晰的概念，最有效的方法就是转到数字的计算上去。这方面的创始工作是埃农（Michel Henon）和海勒斯（Carl Heiles）在1964年作出的（见参考文献），自那以后又由许多人如约翰·福特（John Ford）和他的同事们进一步发展了（Balescu，1975）. 计算通常是对两个自由度的系统，并且是对给定的能量值进行的。这样就剩下三个独立变量（因为给定总能量，就是给出了一个包括两个动量p₁ ，p₂ 和两个坐标q₁ ，q₂ 的条件）。于是编出了一个计算机程序来解运动方程，并把轨道与q₁ p₂ 平面的交点画出图来。为了进一步简化，只画出这些交点的一半，就是说轨道向“上”走的那一半，即q₁ ＞0（见图2.8）。

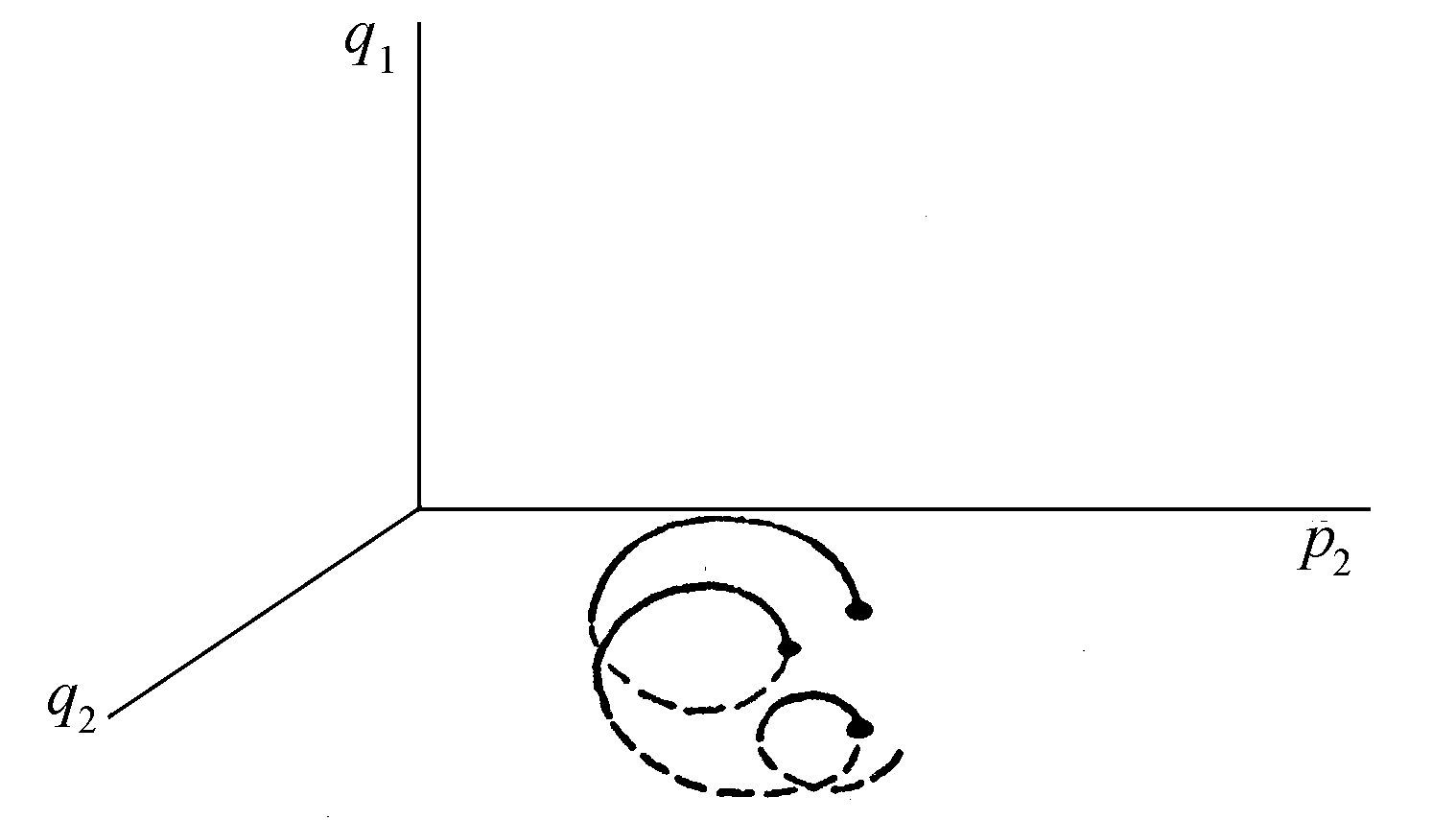
图2.8　埃农-海勒斯系统的一个三维轨道

在这种曾被庞加莱使用过的图上，可以清楚地看出该系统的动力学行为。如果运动是周期性的，交点干脆就是一个点。如果轨道是有条件的周期轨道，即如果轨道被限制在一个环上，则相继的交点将在q₂ p₂ 平面上画出一条封闭曲线。最后，如果轨道是“随机”的，就是说轨道在相空间中无规则地乱跑，则交点也在q₂ p₂ 平面上无规则地乱跑。这三种情况示于图2.9中。

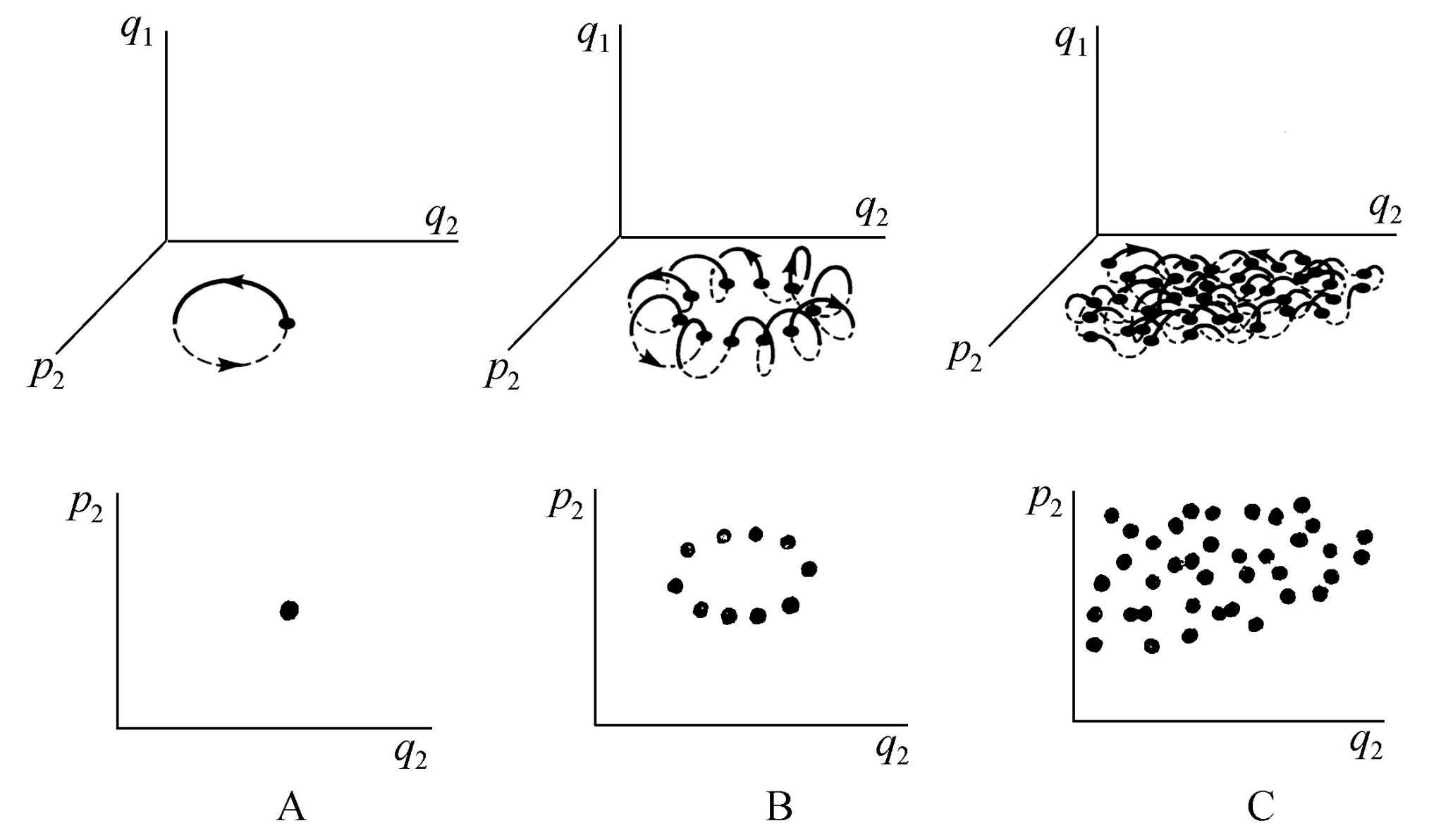
图2.9　各种类型的轨道

（A）周期的；（B）有条件的周期的；（C）随机的。

福特以及其他人所做的一个有趣的观察是，一个动力学系统在一定环境下，可能会从有条件的周期运动过渡到“随机”运动。为了分析这个发现，让我们从下面的哈密顿量出发，它由两项组成，一项是只与正则动量有关的未微扰哈密顿量H₀ ，另一项是既与正则动量有关，又与正则坐标有关的微扰。

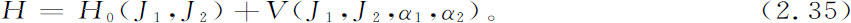
假如没有微扰，则J₁ 和J₂ 就应是与问题相应的作用变量，我们就会有与哈密顿量H₀ 有关的两个“无微扰”频率，并如方程2.27给出的那样为

注意与谐振子情况的一个主要区别是：H_o 通常不是J₁ 、J₂ 的线性函数，这两个频率是作用相关的。

现在我们看一下哈密顿量2.35中微扰V的作用。因为一般地说这是一个角变量α₁ ，α₂ 的周期函数，所以我们可以把它写成傅里叶级数的一般形式。典型地，我们考虑如下形式的微扰：

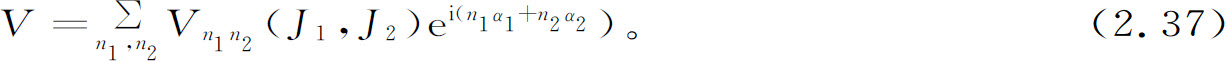
令人感兴趣的是，通过微扰理论，运动方程的解总要含有下列项：

它相当于势能除以无微扰系统的频率总和所得到的比。如果傅里叶系数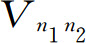 在共振时不为零的话，这将导致“危险”的行为。因为对于共振，有

表达式2.38是不确定的，于是异常的行为就在意料之中了。

正如数字实验所指出的那样，正是由于共振的发生，使得从周期或准周期的行为导向随机的行为（见图2.9）。共振破坏了动力学运动的简单性。共振相当于能量或动量从一个自由度到另一个自由度的大规模转移。在数字计算中，通常只考虑有限数目的共振，比如两个共振。但重要的是要研究，如果共振的数目趋于无穷，即若在J₁ J₂ 平面的每个任意小的区域中都有共振的话，将会发生什么？这种情况相当于以前提过的关于可积系统不存在的庞加莱定理。共振导致了如此不规则的运动，以至运动的不变量，不同于哈密顿量，已不再是作用变量的解析函数了。我们称之为“庞加莱突变”，它将在本书的后面章节中起重要作用。庞加莱突变流行的程度是很惊人的，它出现于从著名的三体问题开始的大多数动力学问题之中。

惠塔克的“adelphic积分”理论（Edmund Wittaker，1937）为庞加莱基本定理的物理意义提供了一个很好的说明。让我们考虑图2.10的作用空间J₁ ，J₂ 中从某点A开始的一条轨道，并考虑该点上的频率ω₁ ，ω₂ 。对于一大类哈密顿量，惠塔克可以通过级数展开从形式上解决运动的问题。但是根据频率ω₁ ，ω₂ 是不是有理独立的（或可通约的），级数展开的类型会是很不相同的。因为ω₁ ，ω₂ 通常是作用变量的连续函数，所以每当它们的比是m/n形式的有理数时，它们就是有理相关的；而如果这个比不是有理数，则它们是有理独立的。因此即使对于两个非常靠近的点A、B，由于每个有理数都夹在无理数之间，反过来每个无理数也都夹在有理数之间，所以运动的类型也是不同的。这就是我们以前已经提到的弱稳定性概念的基本内容。十分清楚，庞加莱突变可以导致“随机”运动。对于可积系统，轨道可以看做是运动不变量的“交线”。例如在两个自由度的情况下，一条轨道对应于两个面J₁ ＝δ₁ 和J₂ ＝δ₂ 的交线，这里δ₁ 和δ₂ 是给定的常数（见方程2.26）。但只要我们有庞加莱突变，这个运动不变量就变为非解析的、“病态”的函数，它们的交线也是如此（见图2.11）。

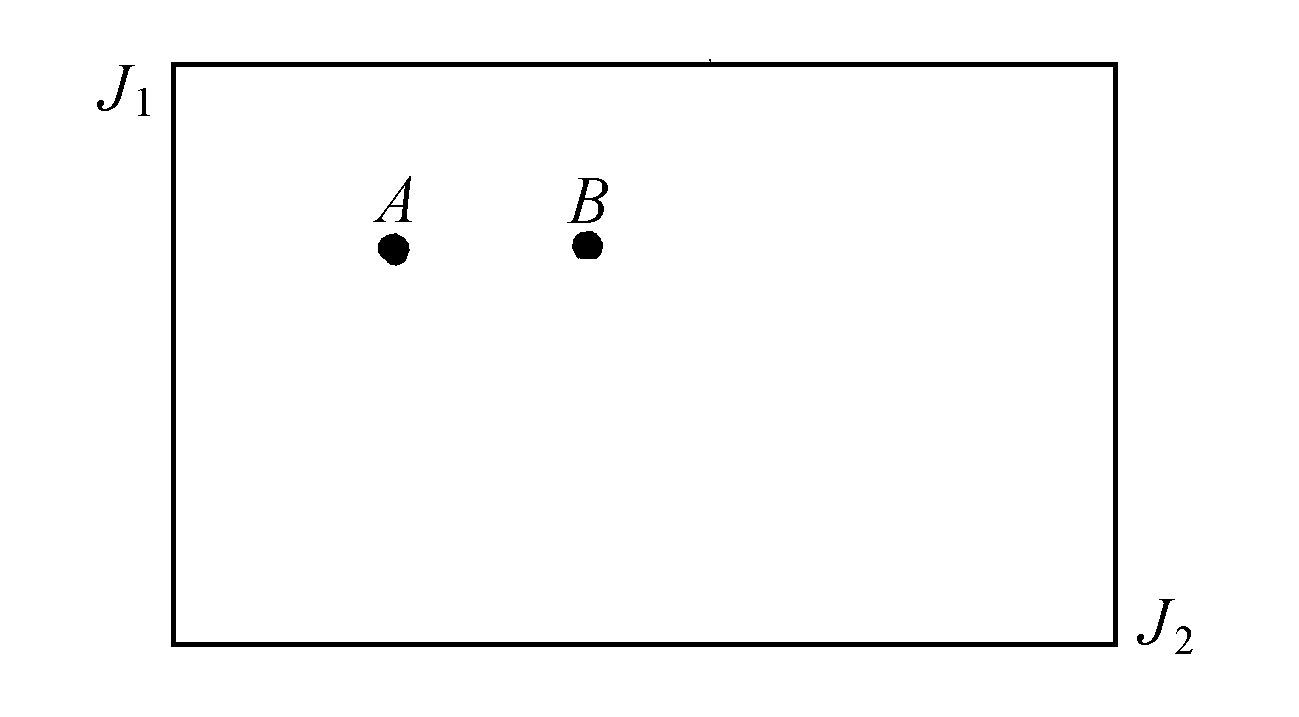
图2.10　惠塔克理论的图示

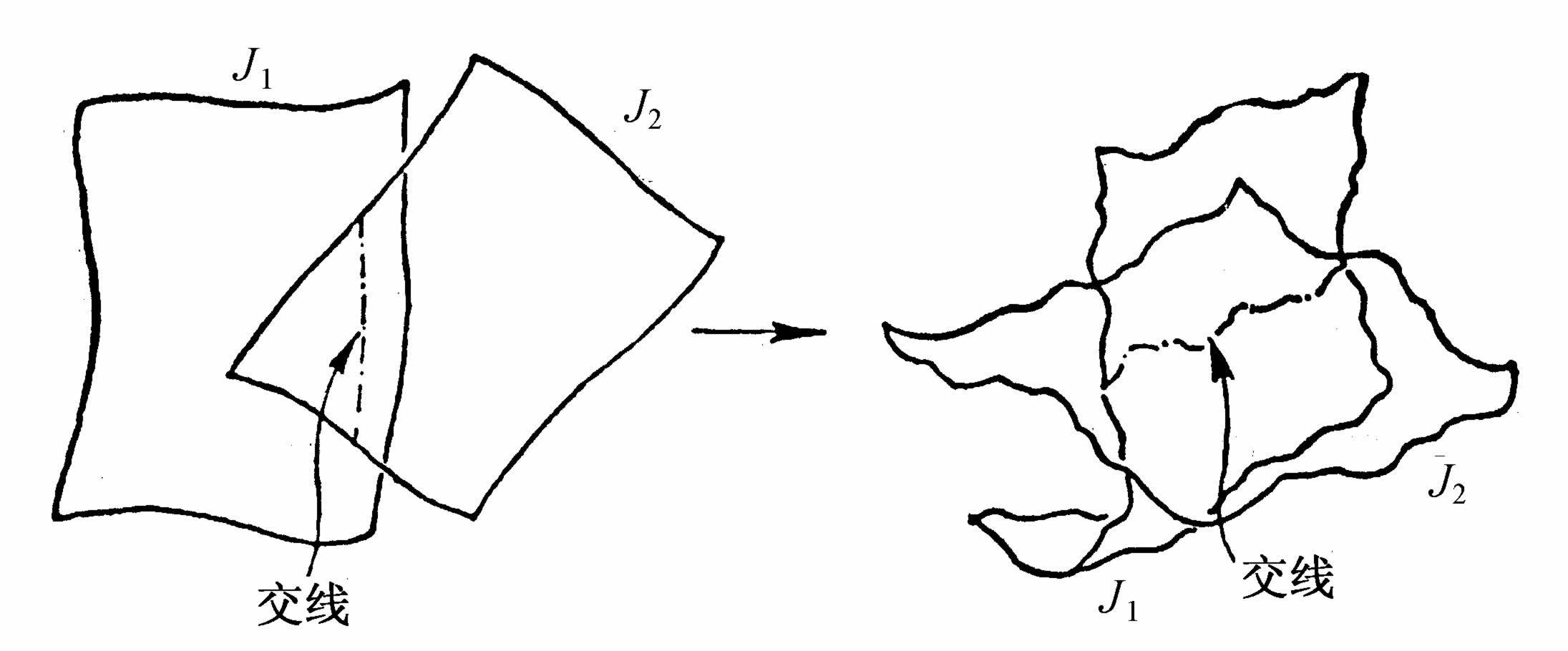
图2.11　相空间中的轨道作为两个不变量面的交线

应当注意，产生庞加莱突变的不可积系统比起遍历系统（或混合系统）来，情况要更加复杂。在不可积系统的情况，我们知道，作为KAM理论的结果，一般地说既存在着局限于有效相空间的某部分上的周期运动，也存在着“覆盖”整个相空间的随机运动。两种类型的运动都可以有正的测度。与此相反，对于遍历（或混合）系统，局限运动的测度是零。我们在下节中分析这种情况的后果。

弱稳定性

我们已经看到，至少有两种情况，动力学运动引入了随机因素。一种情况是混合流动（或满足更强条件的流动，如K流动）；另一种情况，我们称之为庞加莱突变，其中当引入相互作用时，共振会阻止无微扰运动不变量的“连续性”。这两种情况是很不相同的：在第一种情况，动力学系统的特点在于，刘维算符带有十分确定的谱特性（例如连续谱）。而在第二种情况，H分解为两部分H₀ 和V（见方程2.35），这是主要的。但是，无论哪种情况，运动的特点都是这样，即从任意靠近的点发出的两条轨道，随着时间的推移都会变得强烈发散。这相当于通常所说的运动的不稳定性，它对于动力学系统在较长期间内的行为具有明显的重要性。为了把这个行为和在简单系统中发现的行为作一对比，我们考虑一个单摆，其哈密顿量为

其中，第一项是动能，第二项是重力场中的势能。坐标q在这里换成了θ，即偏角。

这个摆可以作两种运动：或者在其平衡位置左右振荡，或者绕其悬点旋转。只有当摆的能量足够大时，才有可能旋转。我们可以在相空间中表示出可能发生一种运动或另一种运动的区域，如图2.12所示。对于我们来说，重要之点在于，对应于振动或旋转的相空间中的相邻点，都属于同一区域。因此，甚至在对系统初态的了解很有限的情况下，我们也能确定系统将是旋转还是振动。

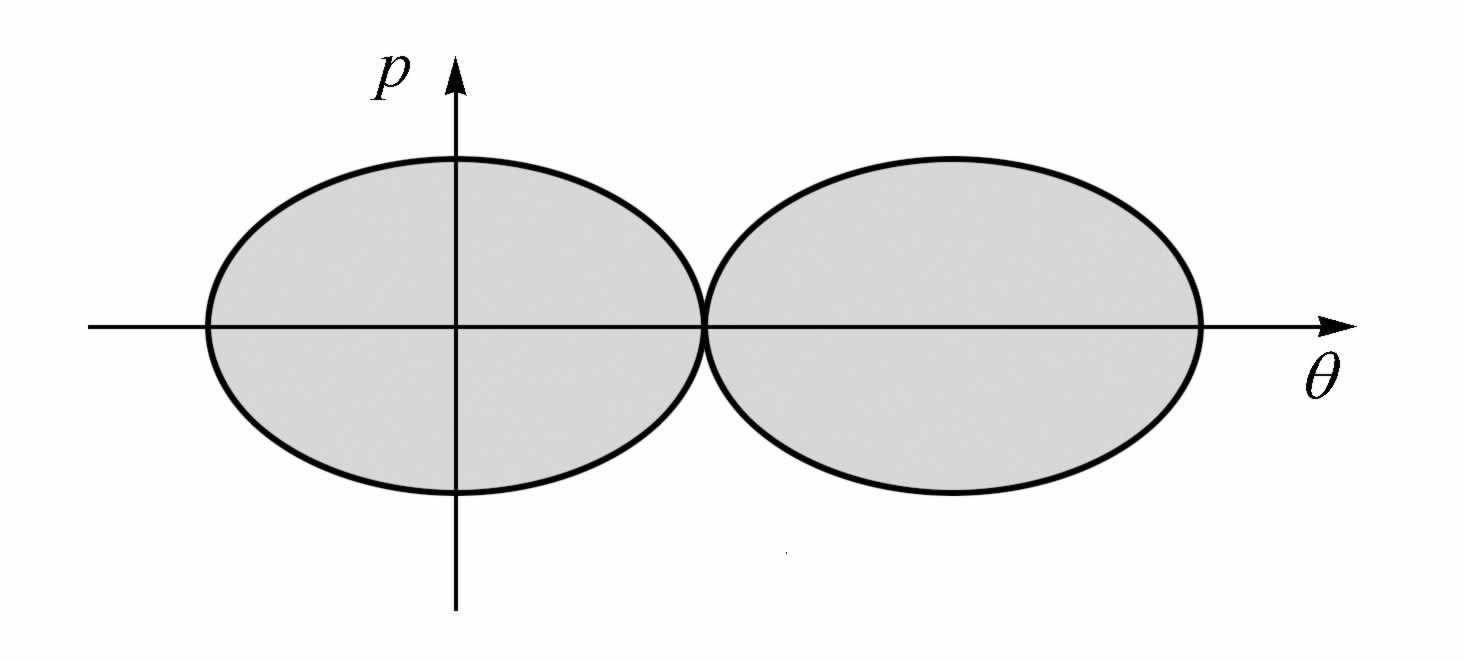
图2.12　旋转器的相空间

阴影区对应于振动，阴影外的区域对应于旋转。

对于只具有弱稳定性的系统，这个性质失掉了。在这样的系统里，我们可以在一种运动的邻域里找到另一种运动（见图2.13）。因为这个性质是始终保持着的，所以不存在要求我们提高观测精度的观点。于是相空间的微观结构就具有极端的复杂性。这就是为什么统计的观点进入到每一个长期预报中去的原因。

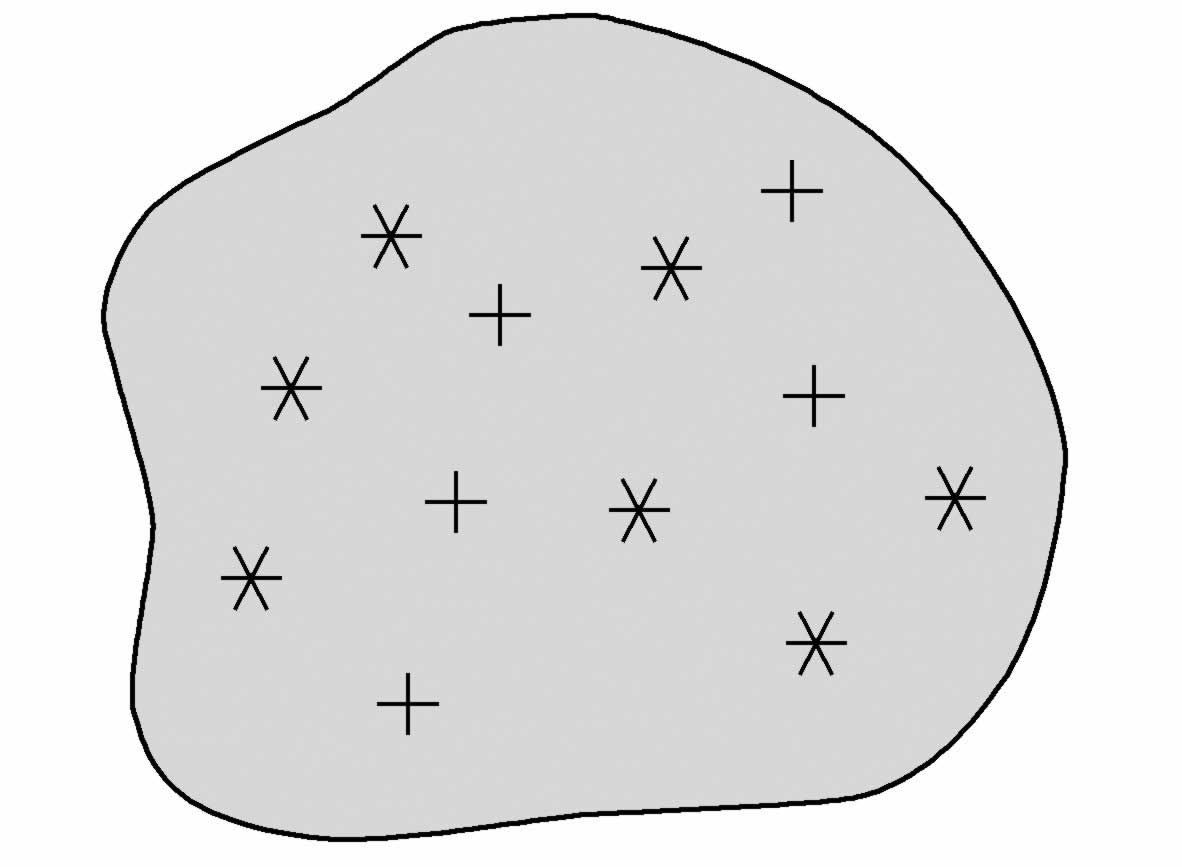
图2.13　弱稳定性系统的示意

在星号所示运动的邻域里我们可找到加号所示的运动。

在这样的情况下我们必须考虑统计系综。我们不能把“混合”情况还原到和一条单一轨道相应的“纯”的情况（单一轨道在相空间中表示为一个δ函数）。这是一个实践性困难还是一个理论性困难呢？我支持这样的观点：这个结果具有重要的理论和概念上的意义，因为它迫使我们越过纯动力学描述的极限。一个类似的问题——光速对信号传播的极限是一个实践问题还是一个理论问题呢？——已由相对论作出了回答。相对论指出，由于这个极限，我们对于空间和时间的概念必须改变。

试图这样地去描述物质世界，仿佛我们并不是这个世界的一部分，这种作法总是很吸引人的。于是我们可以设想任意的、甚至是无限的传播速度，并确定具有无限精度的初始条件。但是从外面观察世界并不是物理学的目的。物理学是要通过我们的测量，描述在我们面前出现的、我们所从属的物质世界。按照相对论所开创的、量子力学所遵循的思维线索，理论物理学的基本目的就是阐明由测量过程而引入的一般极度。

但是，弱稳定性仅仅是为把时间和不可逆性纳入动力学的形式结构而迈出的一步而已。我们将看到，熵的引入，或一般地说，李雅普诺夫函数的引入，使这个形式结构的整体发生了深刻变化（见第3章和第7章）。这是一个最意想不到的进展。我们原来期望从基本粒子领域里的新发现或是从宇宙进化方面的新见识中，看到新的理论结构的诞生。但最使人惊奇的是，这个和我们已相处了150年之久的热力学不可逆性的概念，要迫使我们去发现新的理论结构。

我们还要强调一下，这个不可逆性问题在经典动力学历史上已经起到了创造性的作用，并且在量子力学中甚至更是如此（见第3章）。热力学的挑战导致了遍历理论和系综理论，并成为一些十分重大进展的起点。这个存在的物理学与演化的物理学之间的富有成果的对话，一直延续到今天。这我们将在第7章和第8章里看到。