第五章　实心球中的热传导

·Chapter V of the Propagation of Heat in A Solid Sphere·

傅立叶主要是一位数学家，而不是物理学家。他主要以数学方法研究热现象，并由此创造出一套数学理论。这并不否认他有深刻的物理思想，也不否认他曾作为一位物理学家工作过。然而，从当时的科学背景和他的研究的理论目的和贡献看，他仍然主要是以他的数学创造而对数学和物理学发生影响，而不是相反。

欧塞尔的驳船广场

第一节　通　解

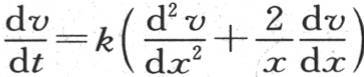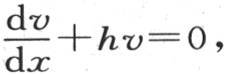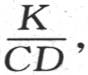283　球中的热传导问题在第二章第2节第117目中已经阐述过了；它在于对方程 进行积分，因此，当x＝X时，这个积分可满足条件 k表示比 h表示两个热导率的比 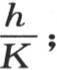v是在历经时间t之后在半径为x的一个球形薄层中所观察到的温度；X是球的半径；v是x和t的一个函数，当我们假定t＝0时，该函数等于F（x）。函数F（x）被给定，并表示固体的初始状态和任意状态。

如果我们令y＝vx，y是一个新的未知数，那么在这个代换之后，我们有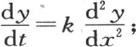 因此我们应当对最后这个方程进行积分，然后取 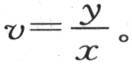首先，我们将考查可以赋予y的最简单的值是什么值，然后形成将同时满足这个微分方程、满足与表面有关的条件，以及满足初始状态的一般的值。不难看到，当这三个条件被满足时，解就是完全的，并且不再有其他的解。

284　设y＝e^mt u，u是x的一个函数，我们有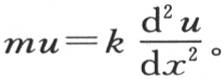 首先我们注意到，当t的值变成无穷的时，v的值在所有点上就都应当为0，因为物体被完全冷却。因此m只可能取负值。现在k有一个正数值，因此我们得出结论，v的值是一个圆函数（circular function），这从方程 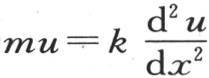的已知性质中得出。设u＝A cosnx＋B sinnx；我们有条件m＝-kn² ，因此我们可以用方程 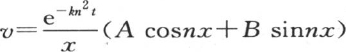来表示v的一个特殊值，这里n是任一正数，A和B是常数。首先我们可以注意到，常数A应当为0；因为当我们使x＝0时，表示中心温度的v值不可能是无穷的；因此项Acosnx应当略去。

此外，数n不可能任意取值。事实上，如果在定义方程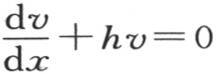 中我们代入v的值，那么我们得到nx cosnx＋（hx－1）sinnx＝0。

由于这个方程应当在表面成立，所以我们在这个方程中假定x等于球半径X，它给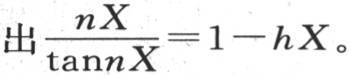

设λ是数1－hX，nX＝ε，我们有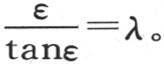 因此我们应当找到一个弧ε，它除以它的正切给出一个已知商λ，然后取 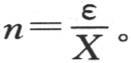显然，这样的弧有无穷多个，它们与它们的正切有一个给定的比，因此这个条件方程 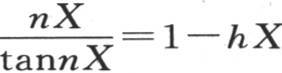有无穷多个实根。

285　作图很适合于揭示这个方程的性质。设u＝tanε（图12）是一条曲线方程，弧ε是这条曲线的横坐标，u是纵坐标；设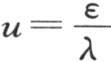 是一条直线方程，它的坐标也由ε和u来表示。如果我们从这两个方程中消去u，我们就有所提出的方程 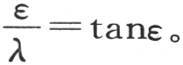因此未知数ε是这条曲线和这条直线的交点的横坐标。这条曲线由无穷多个弧所组成；对应于横坐标 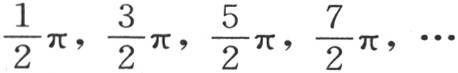的所有纵坐标都是无穷大的，对应于点0，π，2π，3π，…的所有纵坐标则都为0。为了画出其方程为 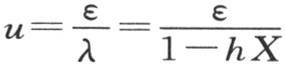的直线，我们作正方形o1ω1，并量出从ω到h的量hX，联结点h和原点o。其方程是u＝tanε的曲线non作为在原点的正切有一条把直线分成两等分的线段，因为这个弧与正切的极限比是1。我们由此得出结论，如果λ或1－hX是一个小于1的量，那么直线mom在曲线non的上方经过原点，并且这条直线与第一个分支有一个交点。同样清楚的是这同一直线截更远的分支nπn，n2πn，…。因此方程 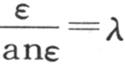有无数实根。第一个根在0到 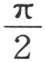内，第二个根在π到 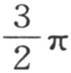内，第三个在2π到 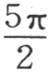内，…。当这些根的序号很大时，它们就很接近于它们的上极限。

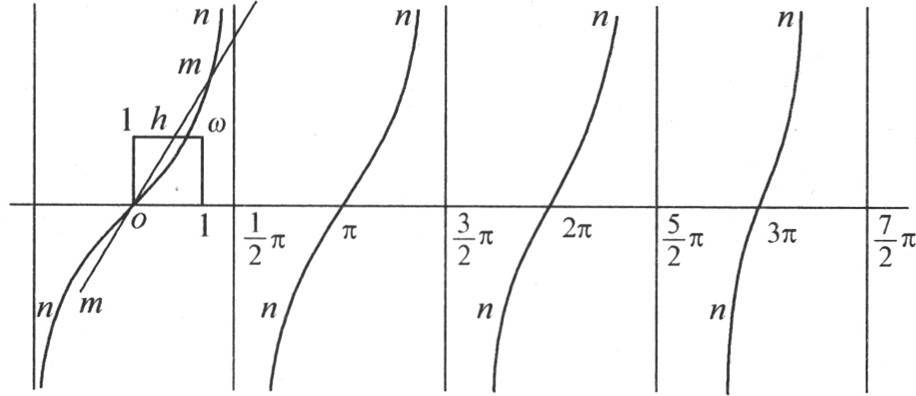
图12 ^【1】

286　如果我们要计算其中一个根，例如第一根的值，那么我们可以应用下述规则：写出两个方程ε＝arctanu和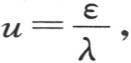 arctanu表示其正切为u的弧的长度，然后对u取任一数，由第一个方程推出ε的值；把这个值代到第二个方程中去，并推出另一个u值；把u的第二个值代到第一个方程中去；因此我们得到一个ε的值，这个值通过第二个方程给出u的第三个值。在第一个方程中代入这个值，我们有一个新的ε值。因此连续用第二个方程确定u，用第一个方程确定ε。这个运算给出愈来愈接近于未知数ε的值。根据下面的作图，这是显然的。

事实上，如果点u对应于（见图13）赋予纵坐标u的任意值，并且如果我们在第一个方程ε＝arctanu中代入这个值，那么点ε就对应于我们由这个方程所计算出的横坐标。如果在第二个方程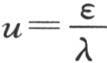 中代入这个横坐标ε，我们将得到一个对应于点u′的纵坐标u′。把u′代入第一个方程，我们得到对应于点ε′的横坐标ε′；然后，把这个横坐标代入第二个方程，它给出一个纵坐标u″，当把这个纵坐标代入第一个方程时，它给出第三个横坐标ε″，以次类推，以至无穷。也就是说，为了表示前面这两个方程连续交替的运用，我们必须从点u向曲线作一条水平线，且从交点ε向直线作一条垂线，从交点u′向曲线作一条水平线，从交点ε′向直线作一条垂线。以次类推，以至无穷，由远而近地愈来愈趋于所要找的点。

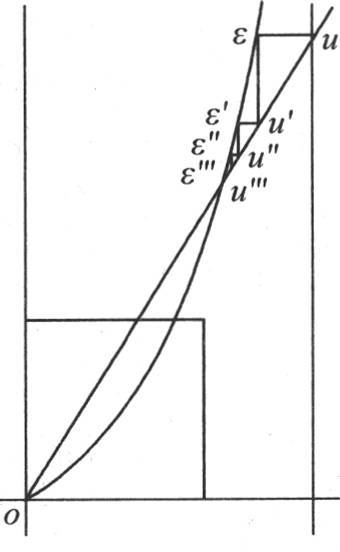
图13

287　上面的图13表示任意为u所选择的纵坐标大于对应于交点纵坐标的情况。另一方面，如果我们为u的初始值选择一个较小的量，并且以同样的方式应用两个方程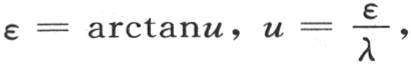 那么我们也会得到逐渐接近于未知值的那些值。图14表明，在这种情况下，我们通过与那些水平线段和垂线段的端点相接的点u，ε，u′，ε′，u″，ε″，…而不断向交点上升。从一个过于小的u值开始，我们得到小于并且收敛于未知值的量ε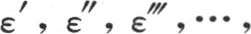， 从一个过于大的u值开始，我们也得到一些收敛于未知值的量，但每一个都比它大。因此我们确定了把要找的量总是包含在内的逐步接近的界限。其中任一次逼近都由公式 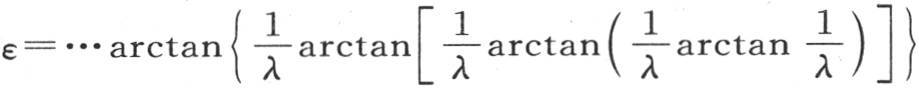来表示。当所指明的几个运算完成后，这一系列的结果就相差得愈来愈小，我们就得到ε的一个近似值。

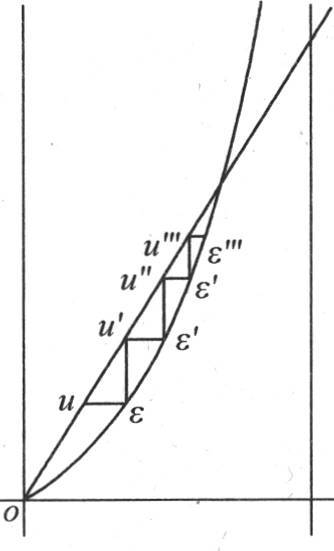
图14

288　对两个方程ε＝arctanu和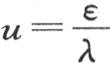 给出u＝tanε和ε＝λu的形式，我们则可以尝试以不同的顺序应用这两个方程。这时我们应当取ε的一个任意值，把它代入第一个方程，我们得到一个u值，这个值代入第二个方程后，它给出ε的第二个值；然后以同样的方式把这个新的ε值应用到第一个方程中去。但是，由作出的图形可知，沿着这个运算过程，我们离开交点愈来愈远，而不是像前面的情况那样逼近它。我们得到的逐个ε值不断减少，一直到0，或者无限增大。我们将依次从ε″到u″，从u″到ε′，从ε′到u′，从u′到ε，直至无穷。

由于我们刚才已经阐明的这个规则可以应用到方程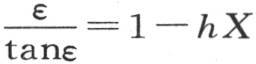 的每个根的计算上去，而且这个方程有给定的范围，所以我们应当把所有这些根都看做是已知数。此外，我们原本只需要确信这个方程有无数实根。我们已经解释了这个逼近过程，因为它以一个著名的作图为基础，这个作图法可以有效地应用到几种情况中去，并且它立即会显示出这些根的性质和范围；尽管如此，这个过程对所说的方程的实际应用可能是冗长乏味的；在实践中采用某种其他逼近方法可能要容易些。

289　我们现在知道，为了满足问题的两个条件，我们可以对函数v给定一个特殊形式，这个解由方程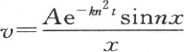 或者是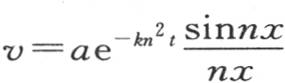 来表示。系数a是任一个数，数n是 中的那个n。由此得到，如果不同薄层的初始温度与商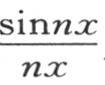 成正比，那么它们都将在整个冷却阶段保持它们已经形成的比而一起降低；每一点的温度将随一条对数曲线的纵坐标而降低，该曲线的横坐标表示历经时间。这样，假定弧ε被等分并取作横轴，则我们在每个界点建立一个等于正弦与该弧的比的纵坐标。这个纵坐标系统指示初始温度，这些初始温度应当在从中心到表面的不同薄层中分布已定，因为整个半径是被等分的。在这个结构下，表示半径X的弧ε不能任意选取；必须是这个弧与它的正切有一个给定的比。由于存在满足这个条件的无数个弧，因此我们可以形成无数个初始温度系统，这些系统在球中自我存在而温度的比在冷却期间不发生任何变化。

290　剩下的问题只是通过一定数量的部分状态或者是无数部分的状态来建立任一初始状态，每一个这样的部分状态都表示我们刚才所考虑过的一个温度系统，其中，纵坐标随距离x而变化，并与正弦和这个弧的商成正比。这样，球内部的一般热运动就分解成许多特殊运动，它们每一个都自由地完成，仿佛它们单独存在似的。

用n₁ ，n₂ ，n₃ ，…表示满足方程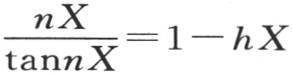 的量，假定它们从最小的一个开始按顺序排好，则我们建立一般方程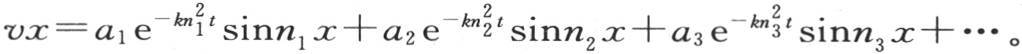

如果使t＝0，那么，作为温度的初始状态的表达式，我们有vx＝a₁ sinn₁ x＋a₂ sinn₂ x＋a₃ sinn₃ x＋…

无论初始状态怎样，问题都在于确定系数a₁ ，a₂ ，a₃ ，…。这样，假定我们知道v从x＝0到x＝X的这些值，并且用F（x）表示这组值，则我们有

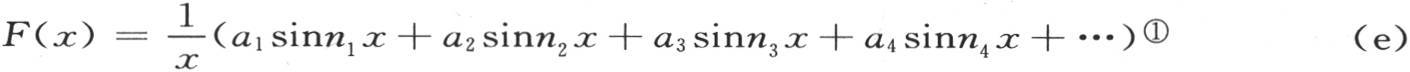
①　关于这种形式的级数表示一个任意函数的可能性，汤姆森爵士给出了一种证明。《剑桥数学学报》，第3卷，第25—27页。——A. F.

291　为了确定系数a₁ ，用x sinnxdx乘方程两边，并从x＝0到x＝X积分。在这些区间之间所取的积分∫sinmx sinnx dx是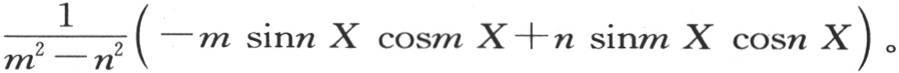

如果m和n是从根n₁ ，n₂ ，n₃ ，…中所选出的数，它们满足方程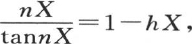 那么我们有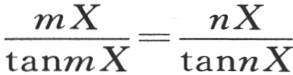 或者是m cosm X sinnX－n sinm X cosnX＝0。

由此我们看到，这个积分的整个值是0；不过存在唯一一种积分不为0的情况，此时m＝n。这时它变成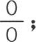 运用已知的规则，它简化成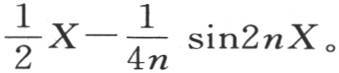

由此得到，为了求出系数α₁ 的值，在方程（e）中，我们应当写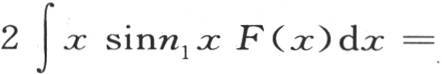 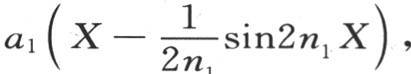积分从x＝0取到x＝X。同样，我们有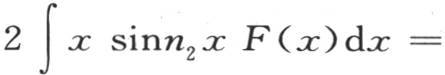

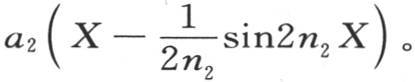
所有后面的系数都可以以同样的方法确定。不难看到，无论任意函数F（x）怎样，定积分2∫x sinnx F（x）dx总有一个确定的值。如果函数F（x）由以任一方式画出的一条曲线的可变纵坐标来表示，那么函数xF（x）sinnx与不难根据第一条曲线所构造的第二条曲线的纵坐标相对应。由第二条曲线在横轴x＝0和x＝X之间所围成的面积来确定系数a_i ，i是根n的序号指标。

任意函数F（x）进入积分符号下的每个系数，并对v值给出问题所要求的所有普遍性；因此我们得到下述方程

这就是对方程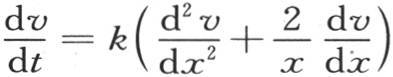 的通积分所应当给出的形式，以使它能表示实心球中的热运动。事实上，这个问题的所有条件都被满足。

第一，满足偏微分方程；

第二，从表面所逃逸的热量同时与最后那些薄层的相互作用一致，并且与空气对表面的作用一致；也就是说，v值的每一部分都满足的方程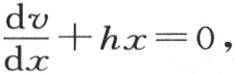 在我们对v取所有这些部分的和时，也成立；

第三，这个给定的解与我们假定时间为0时的初始状态一致。

292　方程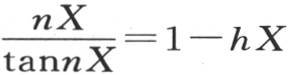 的根n₁ ，n₂ ，n₃ ，…是极不相等的；因此我们得到，如果时间值相当大，那么v值的每一项相对于它前面的项就非常小。随着冷却时间的增加，v值后面的那些部分就不再有任何明显的影响；并且，在开始组成一般运动，以使初始状态能由它们所表示的那些部分状态和基本状态，除一个以外，都几乎完全消失。在终极状态中，不同薄层的温度，以和圆中的正弦与弧的比随弧的增加而减少的同一方式，从中心向表面而降低。这个规律自然地控制着实心球中的热分布。在它开始存在时，它在整个冷却期间都存在。无论表示初始状态的函数F（x）如何，所说的这个规律都不断趋于形成，当冷却延续一段时间后，我们就可以假定它存在而不会有明显的误差。

293　我们把这个一般解应用到一个球在某种液体中浸泡很长时间，其所有点都得到相同温度的情况中去。在这种情况下，函数F（x）为1，系数的确定归结为从x＝0到x＝X对x sinnxd x进行积分：该积分是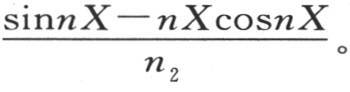 这样，每个系数的值因而表示为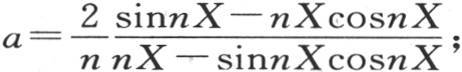： 系数的顺序由根n的顺序所确定，给出n的这些值的方程是 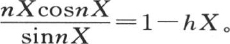因此我们得到 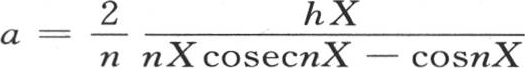。 ^【2】

现在不难建立由方程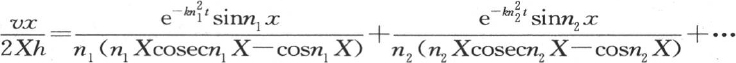 所给出的一般值。

用ε₁ ，ε₂ ，ε₃ ，…表示方程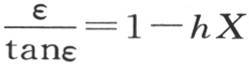 的根，并假定它们以最小的一个开始按顺序排列；用ε₁ ，ε₂ ，ε₃ ，…来代替n₁ X，n₂ X，n₃ X，…，用k和h的值 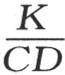和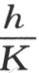 来代替k和h，这样，对于均匀受热的实心球在冷却期间的温度变化的表达式，我们有方程

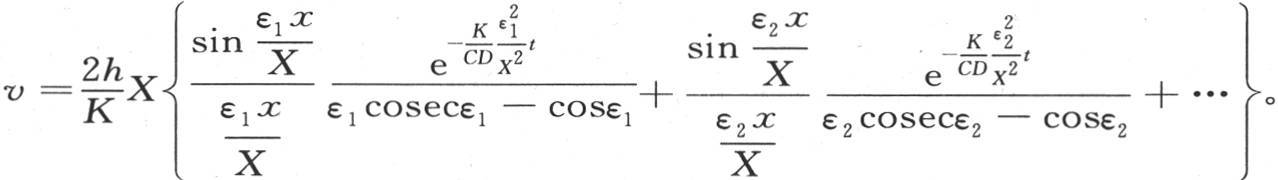
注：黎曼很全面地讨论过球的问题，《偏微分方程》，§§61—69。——A.F.

第二节　对这个解的各种注记

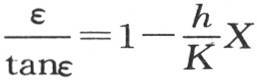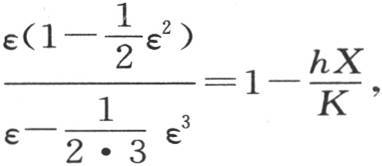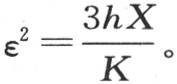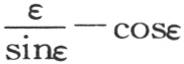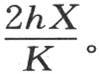294　现在我们来解释从前面的解可以导出的某些结果。如果我们假定系数h有很小的值，它衡量热据以进入空气的能力，或者是，球半径X非常小，那么ε的最小值就变得很小；因此，方程 化为 或者，略去ε的高次幂， 另一方面，在同一假定下，量 变成 项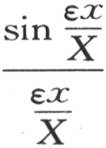 化为1。只要在一般方程中作这些代换，我们就有 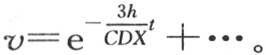我们可以注意到，与第一项相比，后面那些项减少得非常快，因为第二个根n₂ 比0大许多；因此，如果量h和X中的一个有很小的值，那么作为温度变化的表达式，我们可以取方程 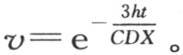所以，在整个冷却期间，组成这个固体的不同球壳保持其共同温度不变。温度随一条对数曲线的纵坐标而降低，时间取作横坐标；在时间t之后，初始温度1化为 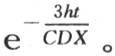为了使初始温度能化成分数 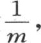t的值就应当是 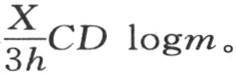因此，在相同物质不同直径的球中，当外热导率很小时，失去它们实际热量的一半或者是同一确定的部分所需要的时间，与它们的直径成正比。半径很小的实心球的情况亦如此；在赋予内热导率K一个很大的值时，我们也会得到同样的结果。一般地，当量 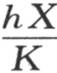很小时这个论断成立。当正在冷却的物体由一种被不断搅拌、并且密封在不厚的球状器皿中的某种液体组成时，我们可以把量 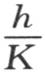看做是很小的。这个假定多少和理想热导率（perfect conducibility）的假定相同；因此，温度随由方程 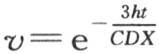所表示的规律而降低。

295　我们由前面的注记看到，在已经冷却很长时间的实心球中，随着正弦与弧的商从等于1的原点到一段给定的弧ε的端点而减少，温度从中心到表面而降低，每个薄层的半径由那个弧的可变长度来表示。如果球的直径很小，或者如果它的内热导率比外热导率大许多，那么逐个薄层的温度就相差无几，因为表示球半径X的整个弧ε的长度很小。这样，它的所有点都具有的温度v的变化由方程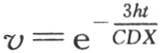 所给出。因此，只要比较两个小球各自在失去它们的实际热量的一半或者是任一相等部分时所耗的时间，我们就会发现，那些时间与直径成正比。

296　由方程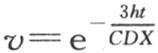 所表示的结果只属于形状相似、体积很小的物体。这早已为物理学家所知，它自然而然地如实呈现出来。事实上，如果任一物体小到足以可以把它在不同点的温度看做是相等的，那么确定其冷却规律就是一件容易的事了。设1是所有点都共有的初始温度；显然，在时刻dt内流进假定保持0度的介质中去的热量是hSvdt，S表示物体的外表面。另一方面，如果C是使单位重量的温度从0度上升到1度时所需要的热量，那么，作为密度为D的物体体积V从0度上升到1度的热量表达式，我们有CDV。所以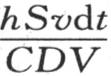， 是当这个物体失去等于hSvdt的热量时，温度v所降低的量。因此，我们应当有方程 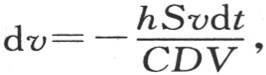或者是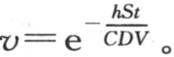 如果物体的形状是半径为X的球形，那么我们有方程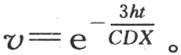

297　假定在所说的这个物体的冷却期间我们观察到对应于时间t₁ 和t₂ 的两温度v₁ 和v₂ ，则我们有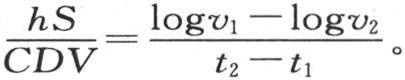 这样，我们就容易用实验来确定指数 如果对不同的物体作同样的观察，如果我们事先知道它们的比热C和C′的比，那么我们就可以得到它们的外热导率h和h′的比。反过来，如果我们有理由把两个不同物体的外热导率h和h′的值看做是相等的，那么我们就可以确定它们比热的比。我们由此看到，通过观察相继密封在不厚的同一容器中的不同液体和其他物质的冷却时间，我们就可以精确地确定这些物质的比热。

此外，我们可以注意到，测量内热导率的系数K不进入方程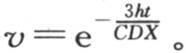 因此，体积小的物体的冷却时间不依赖于内热导率；关于后者的性质，这些时间的观察不可能告诉我们任何东西；但是我们可以通过测量不同厚度的容器中的冷却时间来确定它。

298　我们在上面对体积小的球的冷却所说的这些内容适合于空气中和液体中的温度计的热运动。对于这些仪器的使用，我们补充以下的注记。

假定一个水银温度计被浸在装满热水的容器中，这个容器在恒温空气中自由冷却。我们要求温度计的温度连续下降的规律。

如果液体的温度不变，并且温度计浸入其中，那么它的温度会发生变化，它迅速接近液体的温度。设v是温度计所指示的变化温度，即它超过空气温度的高度；设u是液体温度超过空气温度的高度；t是对应于这两个值v和u的时间。由于在要历经的时刻dt开始时，温度计与液体的温差是v－u，所以变量v趋于降低，并且在时刻dt内失去与v－u成正比的一个量；因此我们有方程dv＝-h（v－u）dt。在同一时刻dt内，变量u趋于降低，它失去与u成正比的一个量，因此我们有方程du＝-Hudt。系数H表示液体在空气中的冷却速度，一个由实验不难发现的量，系数h表示温度计在这种液体中的冷却速度，后一个速度比H大得多。同样，我们可以在使温度计在保持恒温的液体中冷却时根据实验来求系数h。这两个方程du＝-Hudt和dv＝-h（v－u）dt，或者是u＝Ae^-Ht 和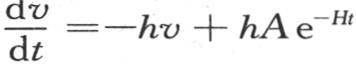 导出方程v－u＝be^-ht ＋aHe^-Ht ，a和b是任意常数。现在假定v－u的初始值是∆，即温度计以∆超过在浸泡开始时液体真实温度的高，u的初始值是E。我们可以确定a和b，并且我们有 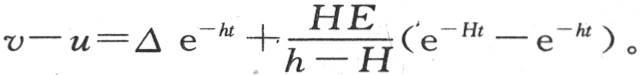量v－u是温度计的误差，即在由温度计所指示的温度和液体在同一时刻的实际温度之间所发现的差。这个差是变化的，并且，上一个方程告诉我们它以什么规律而减少。我们由差v－u的表达式看到，它含有e^-ht 的这两个项减少得非常快，如果温度计浸在恒温液体中，那么这个速度可在温度计中看到。至于含有e^-Ht 的项，它减少得很慢，并受到容器在空气中的冷却速度的影响。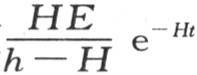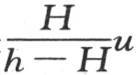由此得到，在不太长的时间之后，温度计的误差由单个项 或者是 来表示。

299　现在考虑什么实验告诉我们关于H和h的值。我们把一个先已受热的温度计浸在8.5°（80进制温标）的水中，它在6秒钟内在水中从40下降到20。我们把这个实验仔细地重复了几次。由此我们得到e^-h 的值是0.000042 ^【3】 ；如果时间以分来计算，也就是说，如果温度计的高度在一分钟的开始时是E，那么在这一分钟结束时它将是E（0.000042）。因此我们得到hlog₁₀ e＝4.3761271。 ^【4】 同时，让一个盛满加热到60°的水的瓷容器在12°的空气中冷却。在这种情况下可看到e^-H 的值是0.98514，因此，Hlog₁₀ e的值是0.006502。我们由此看到分数e^-h 的值多么小，并且看到，在一分钟之后，乘以e^-ht 的每一项还不足它在这一分钟开始时的千分之五。因此我们不必在意v－u值中的那些项。这个方程变成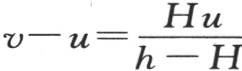 或者是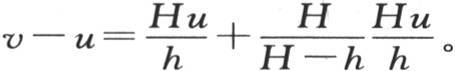 从求H和h的这些值我们看到，后一个量h比H大673倍多，也就是说，温度计在空气中冷却要比容器在空气中冷却快600多倍。因此，项 肯定比水的温度超过空气温度的高度的600分之一还小，项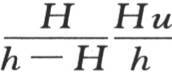 同样比前一项的600分之一还小，而前一项已经够小的了。由此得到，我们可用来很精确地表示温度计误差的方程是 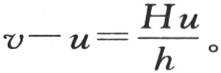一般地，如果h相对于H是一个很大的量 ^【5】 ，那么我们总有方程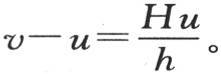

300　我们刚才所作的研究为温度计的比较提供了非常有用的结果。

由一个浸在正在冷却的一种液体中的温度计所示的温度总是稍大于这种液体的温度。温度计的这个超出量或误差随温度计的高而异。用容器在空气中的冷却速度H与温度计在液体中的冷却速度h的比乘温度计的实际高度u，可以得到校正量。我们应当假定在温度计在当初浸入液体时它所示出的是一较低的温度。这就是为什么在开始时温度计几乎总是接近于液体温度而此种状态又不持续下去的原因；在液体冷却的同时，温度计首先经过与液体相同的温度，然后它指示稍稍不同并且总是偏高的温度。

300^* 　我们由这些结果看到，如果我们把不同的温度计浸在盛满正慢慢冷却的液体的同一个容器中，那么它们肯定在同一时刻都很接近地指示同一温度。把h，h′，h″，…称为这些温度计在液体中的冷却速度，我们把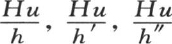 作为它们各自的误差。如果两个温度计同样灵敏，即如果量h和h′相同，那么它们的温度同样不同于液体温度。系数h，h′，h″，…的值很大，因此温度计的误差是极其小、并且常常不易察觉的量。由此我们得到，如果精心制作一个温度计，并且可以把它看做是精确的，那么就不难制作其他几个精度相同的温度计。这只需把我们要校准的所有温度计放进盛满慢慢冷却的液体的容器中，同时把用来作为标准的温度计放进去就够了。我们只需一度一度地，或以更大的间隔来观察，我们应当标出在同一时刻在不同温度计中所看到的水银位置的点。这些点是所需要的刻度。我们曾把这个过程应用到我们的实验中所使用的温度计的构造上，结果这些仪器在相同环境中总是一致的。

温度计在冷却期间的比较不仅建立了它们之间理想的一致性，为它们全都提供相同的单一模型；而且我们由此得到精确刻画主要温度计管的方法，由这种方法，所有其他温度计都应当能校准。由此可见，我们满足这种仪器的基本条件，这就是，在包含相同度数的刻度上，任意两个间隔包含相同的水银量。至于别的，我们在此处省略了不直接属于我们著作目的的几个细节。

301　在前面几目中，我们确定了由距球心x的一个内球形薄层在历经时间t之后所得到的温度v。现在要做的是计算球的平均温度的值，或是计算在它所包含的全部热量在整个物体中都等分布时该物体所具有的值。由于半径为x的球的体积是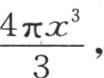 所以，包含在温度为v，半径为x的球壳中的热量是 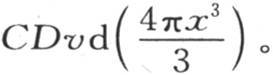因此平均温度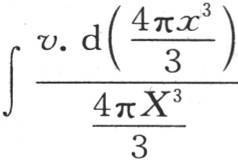是 或者是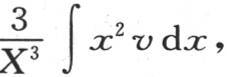 积分从x＝0取到x＝X。用v的值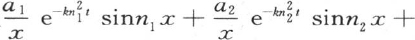 代替v，我们有方程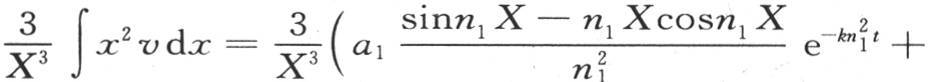

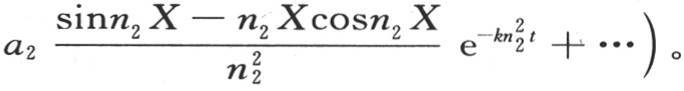
我们在前面（第293目）曾得到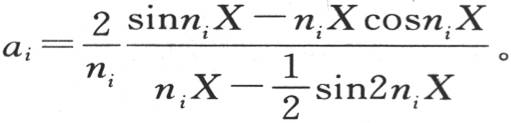 因此，如果我们用z表示平均温度，那么我们有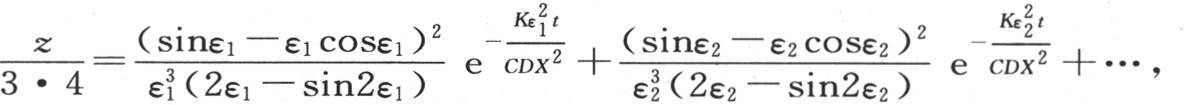

302　让我们考虑所有其他条件都保持相同而球半径的值X变得无穷大时的情况 ^【6】 。在采用第285目所描述的作图时我们会看到，由于量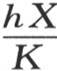 变成无穷的，所以，过原点所作的切割这条曲线不同分支的直线与x轴重合。这样，对于ε的不同值，我们得到量π，2π，3π，…。

由于当时间增加时包含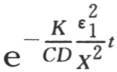 的z值的这个项比后面的项大很多，所以在一定时间之后，只用第一项来表示z的值不会有明显的误差。由于指数 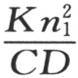等于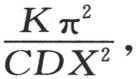 所以我们看到，在大直径的球中，最后的冷却是非常慢的，并且，测量冷却速度的e的指数是直径平方的倒数。

303　我们根据前面几个注记可以对固体球在冷却期间所服从的变化形成一个精确的思想。当热通过表面而耗散时，温度的初始值依次变化。如果不同薄层的温度在开始时是相等的，或者如果它们从表面递减到球心，那么它们就不再保持它们最初的比，在所有情况下该系统都愈来愈趋于一个稳定状态，延续不久之后，就明显达到这个状态。在这个最后的状态中，温度从球心到表面逐步降低。如果我们用小于周长四分之一的某个弧表示球的整个半径，并且在等分这些弧之后，对每一点取正弦与该弧的商，那么，这组比就表示在厚度相等的薄层的温度之间所自然形成的比。从这些终极比出现的时间开始，它们就在整个冷却阶段自始至终存在。这时，每一温度都随一条对数曲线的纵坐标而降低，时间取作横轴。我们可以断定，这个规律通过观察几个连续值z，z′，z″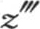， ，…而建立，这些连续值表示相对于时间t，t＋Θ，t＋2Θ，t＋3Θ，…的平均温度；这一系列值总是收敛于一个几何级数，当逐个商 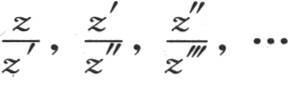不再变化时，我们得到，所说的这种联系就在这些温度之间建立起来。当球的直径很小时，一旦物体开始冷却，这些商就明显地变得相等。冷却时间，作为一个给定的区间，也就是说对于平均温度z被降为它本身的一个确定部分 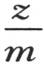时所需要的时间，随球的直径的扩大而增加。

304　如果物质相同体积不同的两个球已经达到当温度降低时它们仍然保持其比的终极状态，并且，如果我们要比较这两个物体冷却同一度数的时间，即比较第一个的平均温度在变成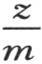 时所用的时间Θ和第二个的温度z′变成 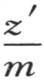的时间Θ′，那么我们应当考虑三种不同的情况。如果两个球的直径都很小，那么时间Θ和Θ′的比就和直径的比相同。如果两个球的直径都很大，那么时间Θ和Θ′的比就成为直径平方的比；如果这两个球的直径界于这两者之间，那么时间的比就比直径的比大，比直径平方的比小。

这个比的精确值已经被确定 ^【7】 。球中的热运动问题包含地球温度问题。为了在更大范围内研究这一课题，我们已辟专章来讨论它 ^【8】 。

305　对上面的方程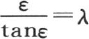 所作的运用以一种几何作图为基础，这个几何作图很适合于解释这些方程的性质。这种作图的确清楚地表明所有的根都是实根；同时它确定它们的范围，指明作为确定每个根的数值的方法。这类方程的分析给出同样的结果。首先，我们可以断定方程ε－λtanε＝0中没有形如 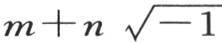的虚根，λ是一个小于1的已知数。这只需用这个量代替ε就够了；在这个变换之后我们看到，当我们对m和n给定实数值时，只要n不为0，左边就不可能变成0。另外我们可以证明，在方程ε－λtanε＝0或者是 中，不可能有任何形式的虚根。

事实上，第一，因子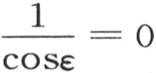 的虚根不属于方程ε－λtanε＝0，因为这些根都有 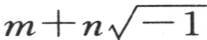的形式；第二，当λ小于1时，方程 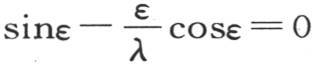的所有根必然都是实根。为证明此命题。我们应当把sinε看做是无数因子的积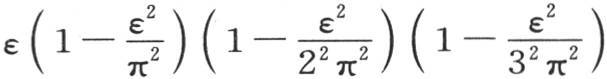 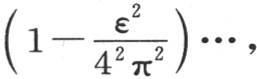把cosε看做是由sinε通过微分而得到的。

假定我们不以无数因子的积来组成sinε，而是只用前m个因子的积，并用φ_m （ε）来表示这个积。为了得到cosε的对应值，我们取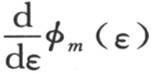 或者是φ′_m （ε）。如此，我们有方程 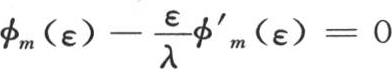。 ^【9】 现在，只要对数m给定从1到无穷的逐个值1，2，3，4，…，我们就通过代数学的一般原理来确定与m的这些不同值所对应的ε函数的性质。我们看到，无论因子数m如何，由它们所产生的ε的方程就都具有所有根均为实根的方程的明显特征。因此，我们严格得到方程 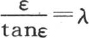不可能有虚根的结论，方程中λ小于1 ^【10】 。同一命题也可由我们在下面某一章中所运用的不同分析推出。

此外，我们所给出的解不以方程所具有的所有根均为实根这一性质为基础。因此，无须用代数分析原理来证明这个命题。对于解的精确性，只要能使积分与任一初始状态一致就够了；因为由此严格得出，它这时也必然表示所有的后继状态。

注释

【1】 　在英译本中，图12中正方形各角上的字母为oiωi，这里的字母是根据法文《文集》本给出的。——汉译者

【2】 　式中的“cosec”是余割符号，即我们现在的“csc”。——汉译者

【3】 　精确地说，是0.00004206。——A. F.

【4】 　在法文《文集》本中，M. 加斯东·达布以一个脚注对这个数据作了说明：h的这个值是利用前一目中的已知公式得到的，在那里，使H＝0，我们有v－u＝∆e^-ht 。——汉译者

【5】 　在英文版中，此句为：“如果H相对于h是一个很大的量”，即把H和h的位置弄反了，现依法文《文集》本校订过来。——汉译者

【6】 　黎曼在《偏微分方程》（Part. Diff. gleich.）§69中已表明，在球很大、最初均匀受热的情况下，表面温度最终随时间的平方根的倒数而变化。——A. F.

【7】 　它是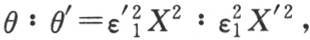 这可以从第301目中z的表达式的第一项的指数推出。——A. F.

【8】 　所说的这一章不在本书之中，它构成“关于固体中热的运动理论的系列论文”（Suite du mémorie sur la théorie du mouvement de la chaleur dans les corps solides）的一部分。

标题为“固体中的热运动理论”（Théorie du mouvement de la chaleur dans les corps solides）的第一个研究报告是1822年发表的《热的解析理论的基础》，但是在现在翻译的这本著作中，它在很大程度上被修改和扩充了。——A. F.

【9】 　在英译本中，此式是φ_m （ε）－εφ′_m （ε）＝0。此处依法文《文集》本校订。——汉译者

【10】 　黎曼的证明更为简单，《偏微分方程》，§67。泊松宣称部分证明方法为他所发现，《科普协会公报》，巴黎，1826，第147页。——A. F.