第三章 无穷矩形固体中的热传导
·Chapter III Propagation of Heat in An Infinite Rectangular Solid·
傅立叶在处理问题时,具有极好的分析技巧和使用符号的才能,定积分符号 就是他建议使用的。他在有关热传导问题中用数学公式将基本物理原理表达得十分详尽和完整,以致后人没有插足的余地。
就是他建议使用的。他在有关热传导问题中用数学公式将基本物理原理表达得十分详尽和完整,以致后人没有插足的余地。

圣·热尔曼修道院附近的小链条葡萄园
第一节 问题的表述
163 根据前述的那些方法,与均匀热传导有关、或者说与固体内变化的热运动有关的一些问题,就转化为纯分析的问题,物理学这一部分的进步因而取决于分析技巧中所能作出的进步。我们已经证明的这些微分方程包含这个理论的主要结果;它们以最一般和最简单的方式表示数值分析与一类非常广泛的现象的必然联系;并且它们永远与数理科学这一自然哲学中最重要的分支之一联系起来。
现在还需要发现这些方程的恰当的处理方法,以便导出它们的全解以及对它们的一种简便的运用。下述问题提供产生这样的解的第一个分析的例子;在我们看来,指明我们所要遵循的方法的原理,是再恰当不过的了。
164 假定一个同质固体物质包含在两个竖直、平行并且无穷的平面B和C之间,并且由垂直于这两个平面的一个平面A分成两部分(图7);我们进而考虑由三个无穷平面A,B,C所界定的这个物体BAC的温度。假定这个无穷固体的另一部分B′AC′是一个恒定热源,即它的所有点都保持温度1并且不发生变化。边界两侧的固体,一侧由平面C和平面A所形成,另一侧由平面B和平面A所形成,它们在所有点上都取恒温0,某一外因总是使它们保持这个温度不变;最后,由A,B和C所界定的这个固体的分子取初始温度0。热将连续从热源A进入这个固体BAC,并在那里沿纵向无穷地传导,同时朝冷物体B和C传导,它们将吸收大部分的热。固体BAC的温度将逐渐升高:但不可能超过、甚至也不能达到最高温度,这种最高温度随这个物体的不同点而异。我们要确定这个变化状态所不断逼近的这个终极和不变的状态。
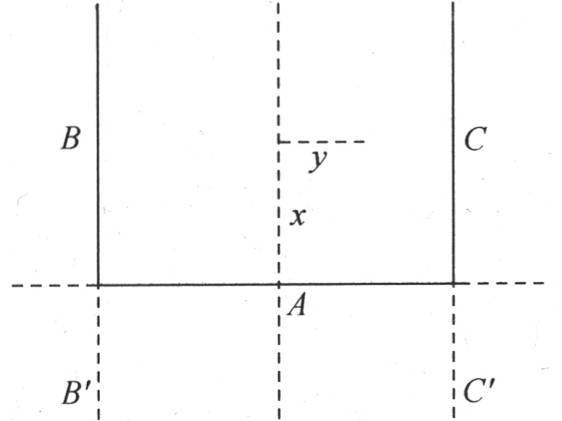
图7
如果这个终极状态已知并且已经形成了,则它会自我保持,这是它区别于所有其他状态的特征。因此,实际问题在于确定由两个冰块B和C及一种沸水物质A所界定的无穷固体的永恒温度;对如此简单和基本的问题的思考,是发现自然现象规律的最纯粹的方式之一,从科学史上看,每一个理论都是以这种方式建立的。
165 为了更简洁地表述这个问题,假定一个无穷长的矩形薄片BAC在基底A被加热,基底的所有点都保持恒温1,同时与基底A垂直的两个无穷边B和C在每一点仍然受恒温0的作用;我们需要确定这个薄片任一点的驻温(stationary temberature)应当是怎样的。
假定这个薄片的表面不失热,或同样的,我们考虑由类似于前述薄片的无数薄片叠加而成的一个固体:取把这个薄片分成两等份的直线Ax为x轴,任一点m的坐标是x和y;最后,薄片宽A,用2l表示,或者,为了简化计算,用直径与圆周长的比值π来表示。
设想坐标为x和y的这个固体薄片BAC的一点m有有效温度v,对应于不同点的量v是这样的:只要基底A的每一点的温度总是1,边B和C在它们所有点上都保持温度0不变,则这些温度不会发生任何变化。
如果在每一点m建立一个等于温度v的纵坐标,那么就形成一个曲面,这个曲面在这个薄片上开拓,并延伸至无穷。我们试图求这样一个曲面的性质:这个曲面经过在y轴上方所作的与y轴相距一个单位的一条直线,并且沿平行于x轴的两条无穷直线与水平面xy相交。
166 为了应用一般方程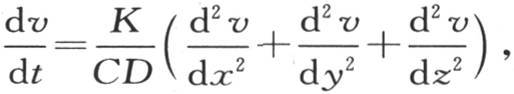 在所讨论的情况中,我们应当考虑排除z轴,因此项
在所讨论的情况中,我们应当考虑排除z轴,因此项 应当略去;由于我们希望确定驻温,所以,相对于左边
应当略去;由于我们希望确定驻温,所以,相对于左边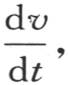 它等于零;因此,属于这个实际问题并且确定所求曲面的性质的这个方程如下:
它等于零;因此,属于这个实际问题并且确定所求曲面的性质的这个方程如下:
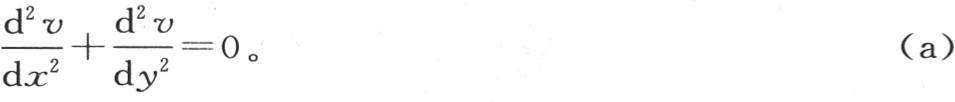
x和y的这个函数,φ(x,y),表示这个固体BAC的永恒状态,第一,它应当满足方程(a);第二,当我们用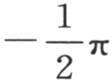 或
或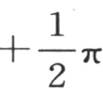 代替y时,无论x的值如何,它应当等于零;第三,当我们假定x=0并且y取
代替y时,无论x的值如何,它应当等于零;第三,当我们假定x=0并且y取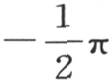 和
和 之间的任意一个值时,它应当等于1。
之间的任意一个值时,它应当等于1。
此外,由于所有的热都来自于热源A,所以,当我们对x给定一个很大的值时,这个函数φ(x,y)就应该变得极其地小。
167 为了在所适合的范围内考虑这个问题,我们首先要求满足方程(a)的x和y的最简单的函数;然后,我们要使v值普通化,以满足规定的所有条件。用这种方法,这个解将得到所有可能的开拓,并且我们要证明,所提出的这个问题不可能有别的解。
两个变量的那些函数,在我们对这两个变量中的一个或者是两个赋予无穷的值时,常常化为不怎么复杂的式子;这就是在这种特殊情况下,在取x的一个函数与y的一个函数的积的形式的代数函数中,所能注意到的。
我们首先要考查这个v的值是否可以由这样的积来表示;由于函数v应当在这个薄片的整个范围内表示薄片的状态,因而也应该包括坐标为无穷的那些点的状态。这样,我们记v=F(x)f(y);在方程(a)中用F″(x)代替并且表示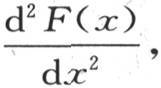 用f″(y)代替并表示
用f″(y)代替并表示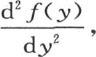 则我们有
则我们有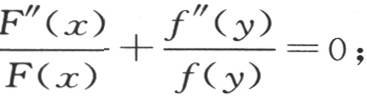 然后我们假定
然后我们假定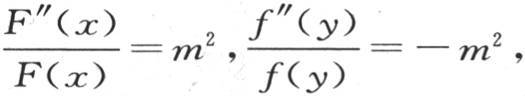 m是任意一个常数,正如仅仅为了求v的一个特殊值而提出的那样,我们从前面这些方程得到F(x)=e-mx ,f(x)=cosmy。
m是任意一个常数,正如仅仅为了求v的一个特殊值而提出的那样,我们从前面这些方程得到F(x)=e-mx ,f(x)=cosmy。
168 我们不可能假定m是一个负数,并且,由于m是一个正数,所以我们应当排除像emx 这样的项会进入其中的所有那些特殊的v值,因为当x无穷大时,温度v不可能成为无穷的。事实上,由于除了恒定热源A之外没有提供任何别的热源,所以只有极小一部分热可以到达离热源很远的那部分空间。余热愈来愈多地向无穷边B和C转移,并且在形成它们的边界的冷物质中耗失。
进入函数e-mx cosmy中的指数m是未知的,我们可以为这个指数选择任意一个正数:不过,为在x无论取什么值而取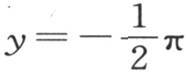 或
或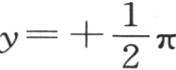 时,v都可以变为零,m就必须取数列1,3,5,7,…中的某一项;第二个条件因这个方法而被满足。
时,v都可以变为零,m就必须取数列1,3,5,7,…中的某一项;第二个条件因这个方法而被满足。
169 把类似于上面那个项的几个项相加,容易得到一个更一般的v值,于是我们有
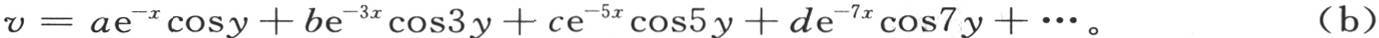
显然,由φ(x,y)表示的函数v满足方程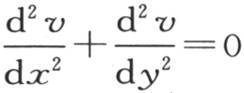 和条件
和条件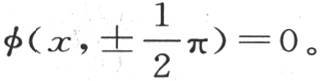 第三个条件也要得到满足,因而它由φ(0,y)=1来表示,应当注意到,当我们对y给定
第三个条件也要得到满足,因而它由φ(0,y)=1来表示,应当注意到,当我们对y给定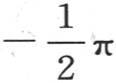 和
和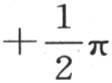 之间的任一值时,这个结果必然成立。如果我们以不包含在界限
之间的任一值时,这个结果必然成立。如果我们以不包含在界限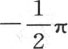 和
和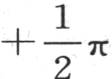 之间的一个量来代替y,那么我们对函数φ(0,y)所可能取的值就不能推出任何东西。因此,方程(b)应当服从下述条件:1=acosy+bcos3y+ccos5y+dcos7y+…。
之间的一个量来代替y,那么我们对函数φ(0,y)所可能取的值就不能推出任何东西。因此,方程(b)应当服从下述条件:1=acosy+bcos3y+ccos5y+dcos7y+…。
数目无穷的系数a,b,c,d,…由这个方程来确定。
右边是y的一个函数,只要变量y在界线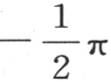 和
和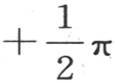 之间,这个函数就等于1。读者或许会怀疑这样一个函数是否存在,不过这个困难在后面会得到彻底解决。
之间,这个函数就等于1。读者或许会怀疑这样一个函数是否存在,不过这个困难在后面会得到彻底解决。
170 在给出这些系数的计算之前,我们可以注意由方程(b)中的级数的每一项所表示的意义。
假定基底A的固定温度不是每点都等于1,而是随直线A的点愈来愈远离中点而下降,与那段距离的余弦成正比;在这种情况下,容易看出纵坐标表示温度v或φ(x,y)的这个曲面的性质是怎样的。如果这个曲面在原点被一个垂直于x轴的平面所截,那么,构成这个截面边界的曲线方程是v=acosy;这些系数的值则如下:a=a,b=0,c=0,d=0,等等,这个曲面方程则是v=ae-x cosy。
如果与y轴垂直地截这个曲面,则截线是凸面朝这个轴的对数螺线;如果与x轴垂直地截它,则截线是凹面朝x轴的三角曲线。
由此得到,函数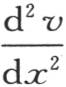 总为正,而
总为正,而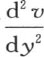 总为负。现在,一个分子所得到的热量因其位置在沿x方向的两个分子之间而与
总为负。现在,一个分子所得到的热量因其位置在沿x方向的两个分子之间而与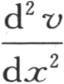 的值成正比(第123目):由此得到,这个中间分子在x方向上从它前面的分子那里所得到的热量比它向它后面的分子所传递的热量多。但是,如果这同一分子被看做是在位于沿y轴方向的两个其他分子之间,因函数
的值成正比(第123目):由此得到,这个中间分子在x方向上从它前面的分子那里所得到的热量比它向它后面的分子所传递的热量多。但是,如果这同一分子被看做是在位于沿y轴方向的两个其他分子之间,因函数 为负,那么,这个中间分子向它后面的分子传递比它从它前面的分子那里所得到的更多的热。因此我们得到,如方程
为负,那么,这个中间分子向它后面的分子传递比它从它前面的分子那里所得到的更多的热。因此我们得到,如方程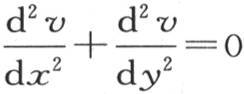 所示,它沿x方向所得到的热的超出量,由它在y方向上所失去的热量严格抵消。因此,从热源A所逃逸的热所流过的路线就成为已知的。它沿x方向传导,同时被分解成两部分,一部分指向某一边,另一部分继续远离原点,像前面那样再被分解,以至无穷。我们所考虑的这个曲面由对应于基底A的三角曲线随它与x轴垂直的平面沿该轴运动而成,它的每个纵坐标与同一分数的逐次幂成正比地无穷减少。
所示,它沿x方向所得到的热的超出量,由它在y方向上所失去的热量严格抵消。因此,从热源A所逃逸的热所流过的路线就成为已知的。它沿x方向传导,同时被分解成两部分,一部分指向某一边,另一部分继续远离原点,像前面那样再被分解,以至无穷。我们所考虑的这个曲面由对应于基底A的三角曲线随它与x轴垂直的平面沿该轴运动而成,它的每个纵坐标与同一分数的逐次幂成正比地无穷减少。
如果基底A的固定温度由项bcos3y或者是ccos5y,…表示,那么我们可以得出类似的推断;用这种方法,可以形成最一般情况下的热运动的精确概念;因为在后面我们会看到,这种运动总是由许多基本运动复合而成,这些基本运动的每一个都像它们单独存在那样被完成。
第二节 热理论中使用三角级数的第一个例子
171 现在取方程1=acosy+bcos3y+ccos5y+dcos7y+…,其中,系数a,b,c,d,…是需要确定的。为使这个方程成立,这些常数当然应当满足由逐次微分所得到的方程;因此下面得出,
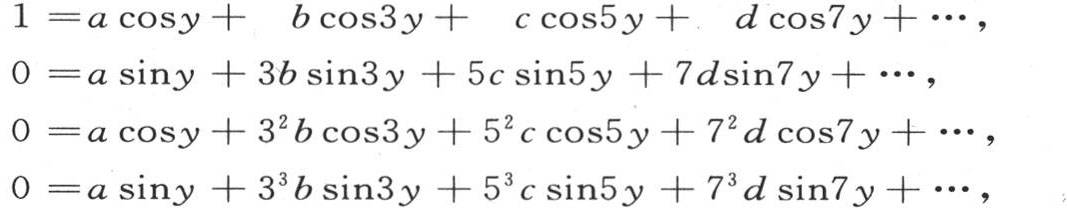
余类推,以至无穷。
当y=0时,这些方程必然成立,因此我们有
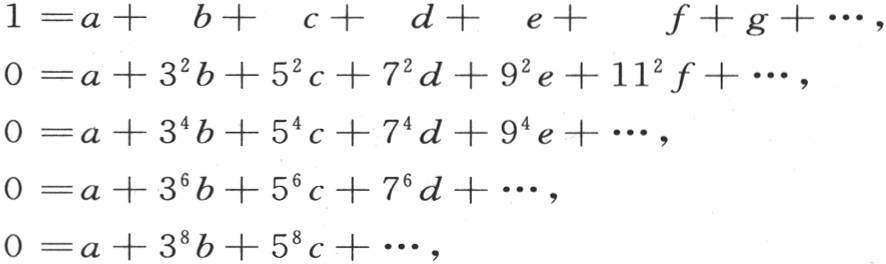
和未知数a,b,c,d,e,…的数目一样,这些方程的个数是无穷的。问题在于只保留一个未知数而消去其他所有的。
172 为了对这些消元结果形成一个清晰的概念,我们假定未知数a,b,c,d,…的数目在开始时是有限的并且等于m。去掉所有那些包含跟着前m个未知数之后的未知数,我们就只运用前m个方程。如果相继使m等于2,3,4,5,…,那么未知数的值就会由每一个这样的假定而求得。例如,对于两个未知数的情况,量a将得到某个值,对于三个、四个,或者是随后更多未知数的情况,它将得到别的值。未知数b亦如此,它将得到和那些消元情况一样多的不同的值;其他每一个未知数同样可以有无穷多个不同的值。现在,对于未知数数目无穷多的情况,其中某一个的值,是它通过逐次消元所得到的那些值所逼近的极限。这样,所要考察的是,随着未知数数目的增加,a,b,c,d,…每一个的值能否收敛于它连续逼近的一个有限的极限。
我们假定使用下面六个方程:
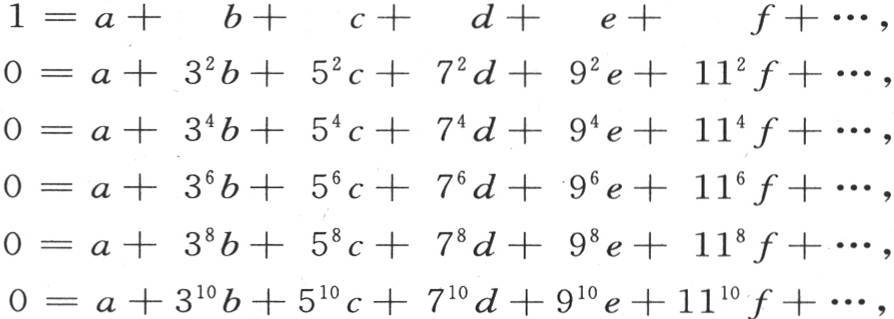
不含f的五个方程是:
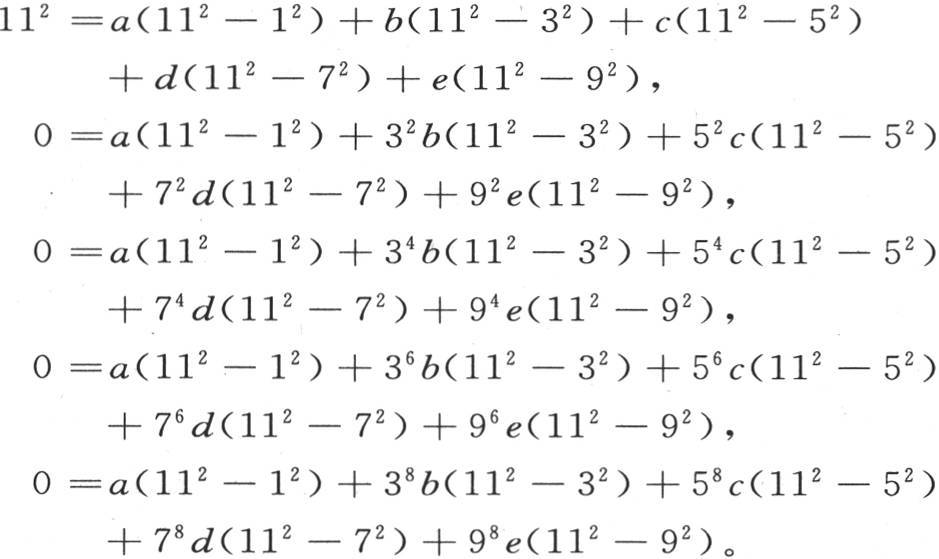
继续消元,我们会得到含a的最后的方程,它是:a(112 -12 )(92 -12 )(7-12 )(5-12 )(32 -12 )=112 ·92 ·72 ·52 ·32 ·12 。
173 如果我们所运用的方程多一个,那么为确定a,我们会得到一个类似于前面的方程,它的左边多一个因子,即132 -12 ,右边有一个新因子132 。a的这些不同的值所服从的这个规律是显然的,由此得到,与无穷数目的方程所对应的a值因而表示为: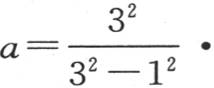
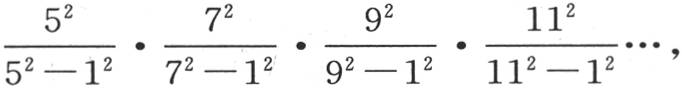 或者是
或者是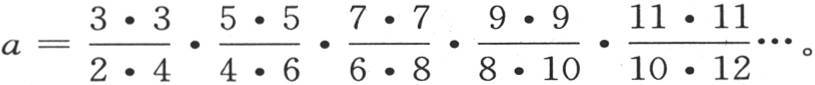
现在,最后这个式子是已知的,根据沃利斯(Wallis)定理 【1】 我们得到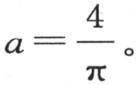 这样就只需确定其他未知数的值了。
这样就只需确定其他未知数的值了。
174 消去f后所剩下的五个方程可以与在假设只有五个未知数时所能运用的五个更简单的方程进行比较。后一种情况下的这些方程与第172目中的那些方程不同,因为在它们中,我们会发现e,d,c,b,a被分别乘以因子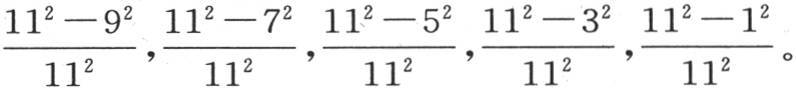
由此得到,如果我们已经解了在五个未知数情况下所应当运用的这五个线性方程,并计算了每个未知数的值,那么就容易由它们推出对应于在应当运用六个方程情况下的同名未知数的值。这只需要用已知因子乘以在第一种情况下所得到的e,d,c,b,a的值就够了。一般地,我们容易从根据一定数目的方程和未知数的假定所取的某个这样的量的值,过渡到在应当多应用一个方程和未知数情况下所取的同一个量的值。例如,如果在五个方程和五个未知数的假定下所得的e值由E表示,那么在多一个未知数情况下所取的同一个量的值,就是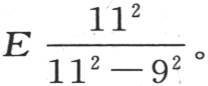 同样,在七个未知数情况下所取的这同一个值,就是
同样,在七个未知数情况下所取的这同一个值,就是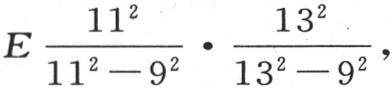 ,在八个未知数的情况下,它是
,在八个未知数的情况下,它是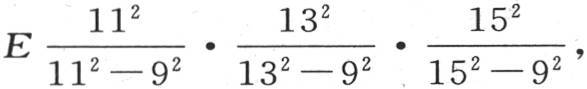 等等。同样,只要知道对应于两个未知数的情况下的b值,就可以由此推出对应于三个、四个、五个等等未知数的情况下的同一字母的值。我们要做的只是把第一个值乘以
等等。同样,只要知道对应于两个未知数的情况下的b值,就可以由此推出对应于三个、四个、五个等等未知数的情况下的同一字母的值。我们要做的只是把第一个值乘以
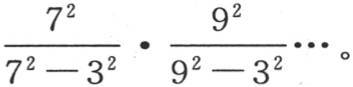
同样,如果我们知道C在三个未知数的情况下的值,我们就可以用连续因子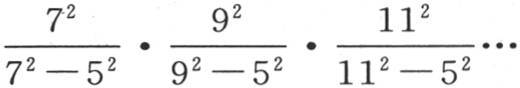 乘这个值。
乘这个值。
我们可以计算d在只有四个未知数情况下的值,并让它乘以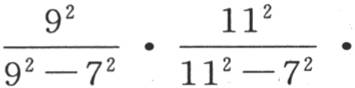
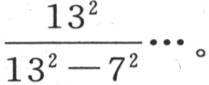
a值的计算服从这同一规则,因为只要取定它对于一个未知数的情况下的值,并依次乘以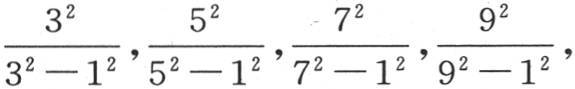 就可以得到这个量的最后的值。
就可以得到这个量的最后的值。
175 因此,问题简化为确定一个未知数的情况下的a值,两个未知数的情况下的b值,三个未知数的情况下的c值,以及等等其他未知数的情况下别的值。
只观察这些方程而无需任何计算,我们就容易得出,这些逐次消元的结果必定是
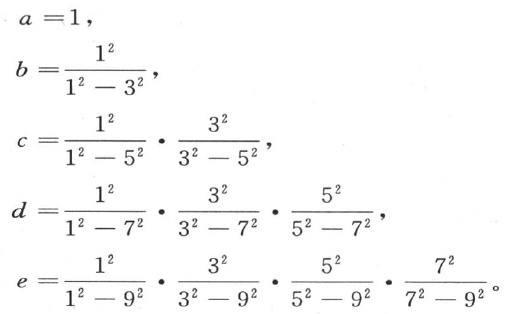
176 剩下来的只是使前面这些量乘以能使它们完整、并且我们已经给出的(第174目)那些积的级数。因此,对于未知数a,b,c,d,e,f,等等的最后的值,我们有下述表达式:
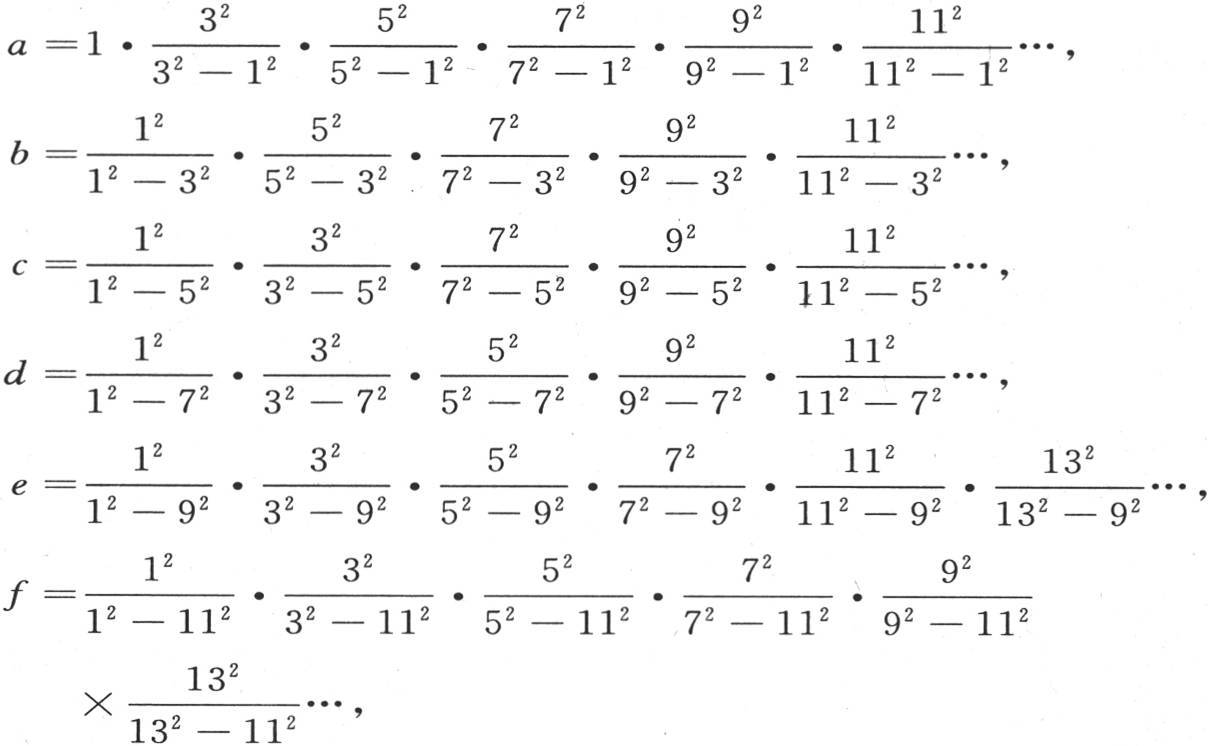
或者是

根据沃利斯定理,量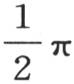 或圆周长的四分之一等于
或圆周长的四分之一等于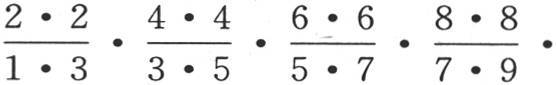

如果现在在a,b,c,d,…的值中,我们注意为了使成对的奇数序列和偶数序列完整而应当加到分子和分母上去的因子是怎样的,那么我们就会发现,要补充的因子分别是:
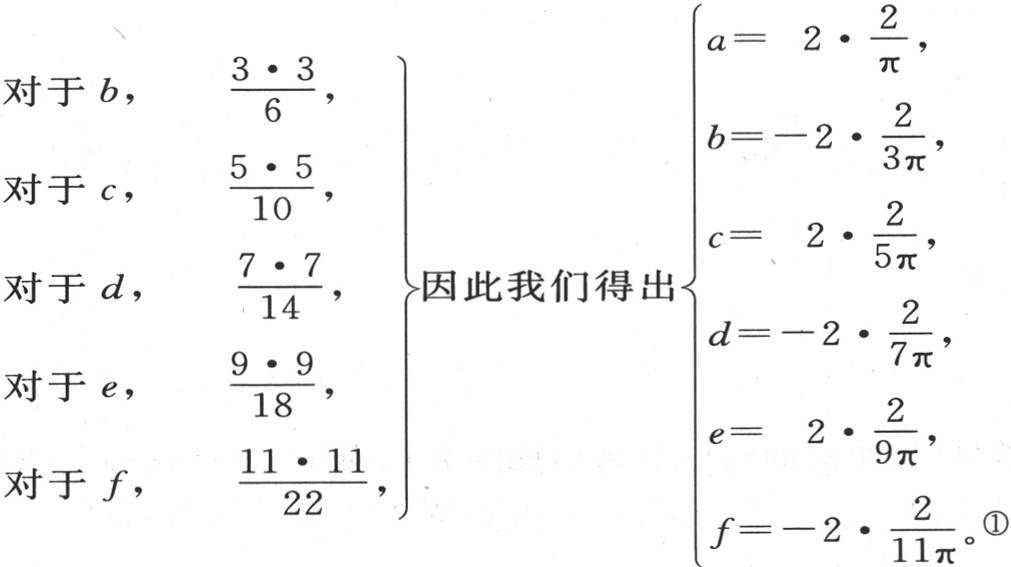
① 由a推出b的值,由b推出c的值,等等,这样要稍稍好一些。——R. L. E.
177 因此我们完全实现了消元,并且确定了方程1=acosy+bcos3y+ccos5y+dcos7y+ecos9y+…中的系数a,b,c,d,…。
这些系数代换给出下述方程: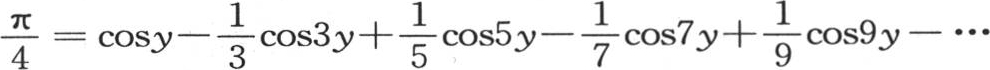 。 【2】
。 【2】
右边是y的一个函数,当我们对变量y给定包含在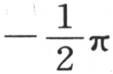 和
和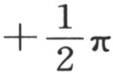 之间的一个值时,该函数的值不变。容易证明,这个级数总是收敛的,即,以任一个数代替y,并遵循这些系数的计算,我们都愈来愈趋近于一个固定的值,因此,这个值与所计算的项的和的差变得小于任一给定的量。无需为读者可以补充的一个证明而停下来,我们注意,如果赋予y的这个值包含在0到
之间的一个值时,该函数的值不变。容易证明,这个级数总是收敛的,即,以任一个数代替y,并遵循这些系数的计算,我们都愈来愈趋近于一个固定的值,因此,这个值与所计算的项的和的差变得小于任一给定的量。无需为读者可以补充的一个证明而停下来,我们注意,如果赋予y的这个值包含在0到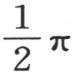 之间,那么不断逼近的这个固定值就是
之间,那么不断逼近的这个固定值就是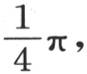 不过,若y包含在
不过,若y包含在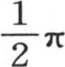 到
到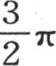 之间,则它等于
之间,则它等于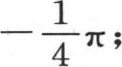 因为在第2个区间里,这个级数的每一项都变号。一般地,这个级数的极限交替为正或负;从别的方面考虑,这种收敛不能快得足以提供一种简便的逼近方式,不过它却足以使方程成立。
因为在第2个区间里,这个级数的每一项都变号。一般地,这个级数的极限交替为正或负;从别的方面考虑,这种收敛不能快得足以提供一种简便的逼近方式,不过它却足以使方程成立。
178 取x为横坐标,y为纵坐标,则方程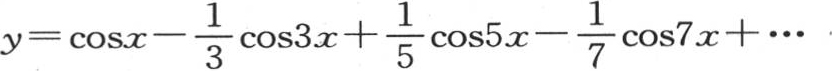 属于由一些分离的直线段所组成的一条曲线,这些直线段平行于轴且等于圆周长。这些平行线交替地位于轴的上方或者是下方,与轴相距
属于由一些分离的直线段所组成的一条曲线,这些直线段平行于轴且等于圆周长。这些平行线交替地位于轴的上方或者是下方,与轴相距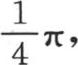 并由本身成为这条线的一部分的一些垂线所连结。为了对这条曲线的性质形成一个精确的概念,应当先假定函数
并由本身成为这条线的一部分的一些垂线所连结。为了对这条曲线的性质形成一个精确的概念,应当先假定函数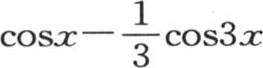
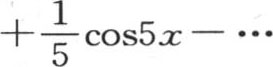 的项数有一个有限的值。在后一种情况下,方程
的项数有一个有限的值。在后一种情况下,方程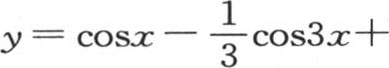
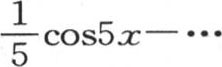 属于一条曲线,这条曲线交替经过横轴的上方或者是下方,同时在每次横坐标x变成等于0,
属于一条曲线,这条曲线交替经过横轴的上方或者是下方,同时在每次横坐标x变成等于0,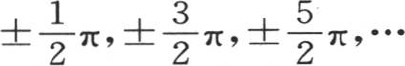 中的某个量时截这个轴。
中的某个量时截这个轴。
随着方程的项数的增加,所讨论的这条曲线就愈来愈趋于和由平行直线和垂线所组成的前面那条线相重合,因此,这条曲线是由逐次增加项数所得到的不同曲线的极限。
第三节 对这些级数的若干注记
179 我们可以从另一种观点来考察同样这些方程,并直接证明方程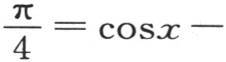
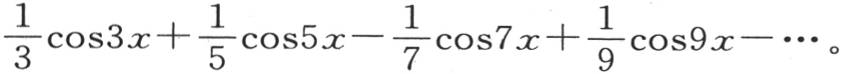
x为零的情况由莱布尼兹级数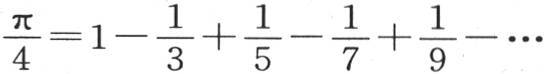 所验证。
所验证。
接下来我们假定级数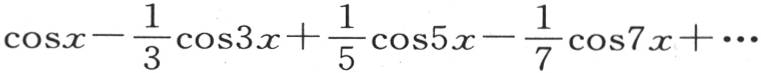 的项数不是无限的而是有限的,并且等于m。我们把这个有限级数的值看做是x和m的一个函数。我们用根据m的负幂所安排的级数来表示这个函数;我们会发现,随着数m变得愈大,这个函数值就愈趋近于一个常数,并且与x无关。
的项数不是无限的而是有限的,并且等于m。我们把这个有限级数的值看做是x和m的一个函数。我们用根据m的负幂所安排的级数来表示这个函数;我们会发现,随着数m变得愈大,这个函数值就愈趋近于一个常数,并且与x无关。
设y是所要求的函数,假定项数m是偶数,该函数由方程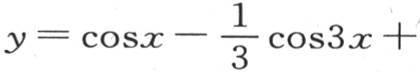
 给出。对x微分后,这个方程给出
给出。对x微分后,这个方程给出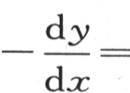 sinx-sin3x+sin5x-sin7x+…+sin(2m-3)x-sin(2m-1)x;乘以2sin2x,我们有
sinx-sin3x+sin5x-sin7x+…+sin(2m-3)x-sin(2m-1)x;乘以2sin2x,我们有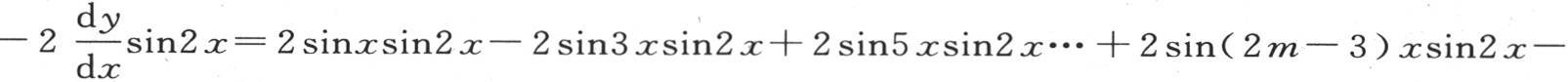
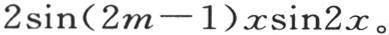
用两个余弦的差来代替右边的每一项,我们得到
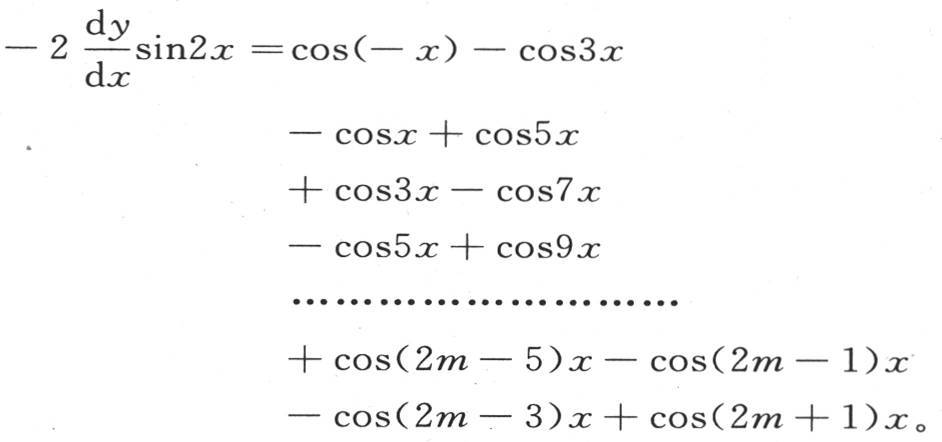
右边简化成cos(2m+1)x-cos(2m-1)x,或者是-2sin2mxsinx;因此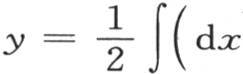
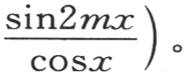
180 我们对右边进行分部积分,同时在这个积分中把应当逐次积分的因子sin2mxdx和应当逐次微分的因子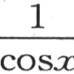 或者是secx区别开;用
或者是secx区别开;用 来表示这些微分的结果,我们有
来表示这些微分的结果,我们有 因此,y,或者是作为x和m的一个函数的
因此,y,或者是作为x和m的一个函数的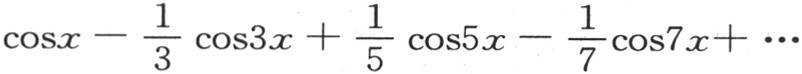
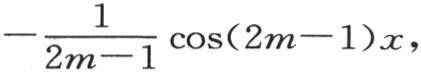 变得由一个无穷级数来表示;显然,数m愈增加,y值就愈趋于不变。由此,当这个数m是无穷的时,这个函数y有一个定值,x的值是一个小于
变得由一个无穷级数来表示;显然,数m愈增加,y值就愈趋于不变。由此,当这个数m是无穷的时,这个函数y有一个定值,x的值是一个小于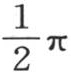 的无论怎样的正值,y的这个定值都是一样的。现在,如果假定弧x为零,我们则有
的无论怎样的正值,y的这个定值都是一样的。现在,如果假定弧x为零,我们则有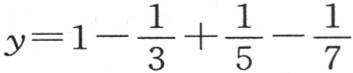
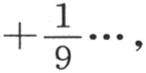 它等于
它等于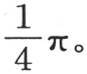 因此,一般地,我们有
因此,一般地,我们有
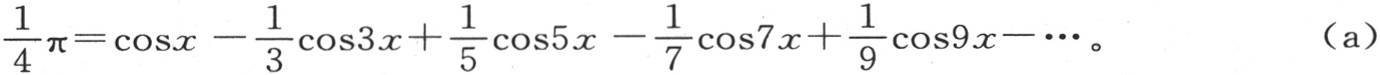
181 如果在这个方程中,我们假定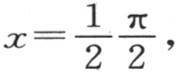 则我们得到
则我们得到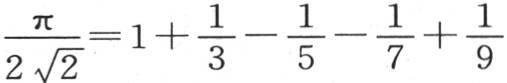
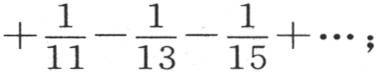 对弧x给定其他的特殊值,我们就得到别的级数,记下这些级数没有用,因为有几个这样的级数已经在欧拉(Euler)的著作中发表了。如果我们用dx乘方程(a),并对它积分,那么我们有
对弧x给定其他的特殊值,我们就得到别的级数,记下这些级数没有用,因为有几个这样的级数已经在欧拉(Euler)的著作中发表了。如果我们用dx乘方程(a),并对它积分,那么我们有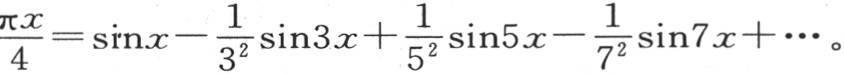
在上个方程中令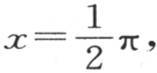 我们得到一个已知级数
我们得到一个已知级数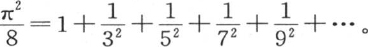 特殊情况可以无限列举,不过,遵循这同一过程来确定由多重弧的正弦和余弦所组成的不同级数的值,这更符合本书的目的。
特殊情况可以无限列举,不过,遵循这同一过程来确定由多重弧的正弦和余弦所组成的不同级数的值,这更符合本书的目的。
182 设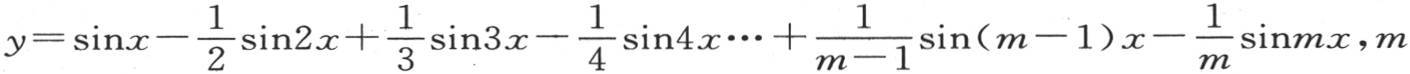 是任一偶数。我们由这个方程推出
是任一偶数。我们由这个方程推出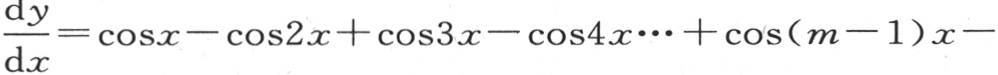
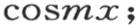 乘以2sinx,并且用两个正弦的差来代替右边的每一项,我们有
乘以2sinx,并且用两个正弦的差来代替右边的每一项,我们有
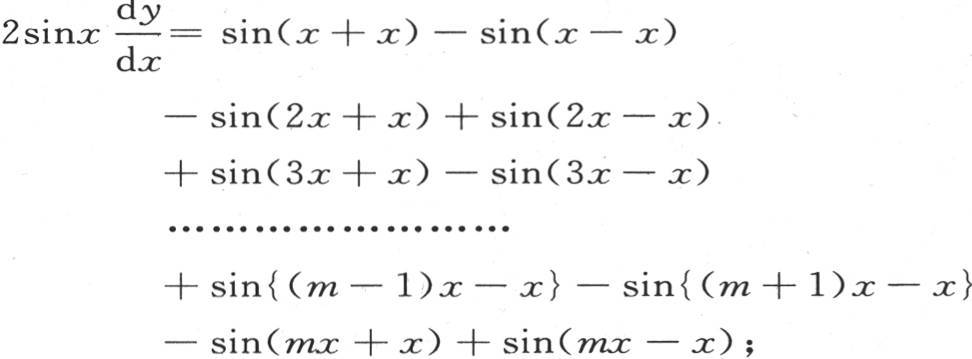
化简,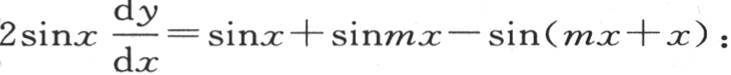 量sinmx-sin(mx+x),或者是
量sinmx-sin(mx+x),或者是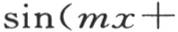
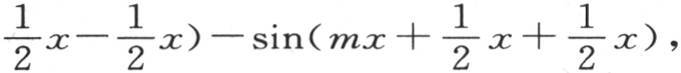 等于
等于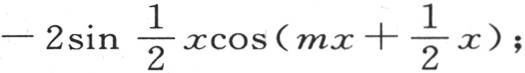 因此我们有
因此我们有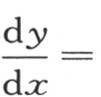
 或
或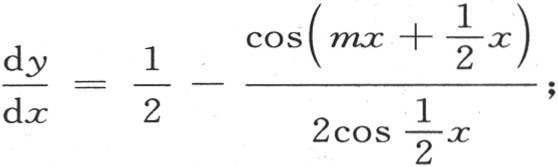
由此我们得到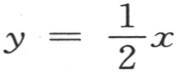
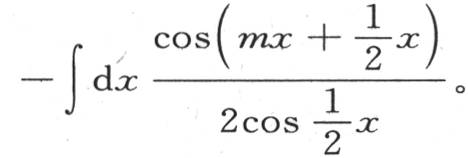
如果我们分部积分,同时区分应当逐次微分的因子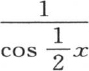 或者是
或者是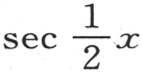 和应当连续几次积分的因子
和应当连续几次积分的因子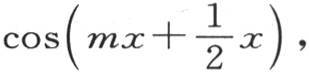 那么我们将形成一个级数,其中
那么我们将形成一个级数,其中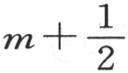 的幂进入分母。至于常数,它等于零,因为y值从x的值开始。
的幂进入分母。至于常数,它等于零,因为y值从x的值开始。
由此得到,当项数很大时,有限级数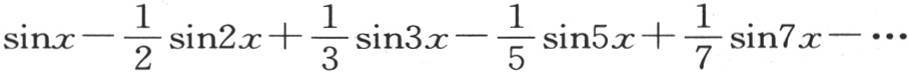
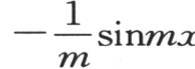 的值与
的值与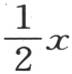 的值相差无几,若项数无穷,则我们有已知方程
的值相差无几,若项数无穷,则我们有已知方程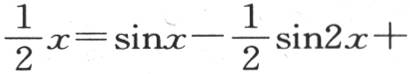
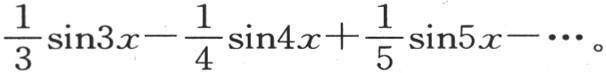
从最后这个级数,还可以推出上面对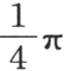 的值所给出的级数。
的值所给出的级数。
183 现在设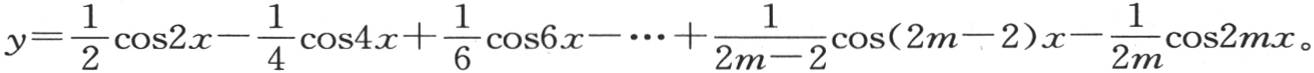
微分,乘以2sin2x,代入余弦的差,并化简,我们得到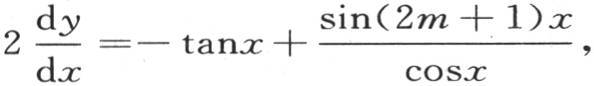 或者是
或者是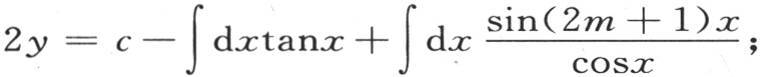 分部积分右边最后一项,并假定m无穷,我们有
分部积分右边最后一项,并假定m无穷,我们有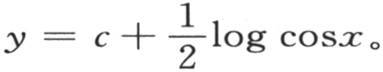 如果在方程
如果在方程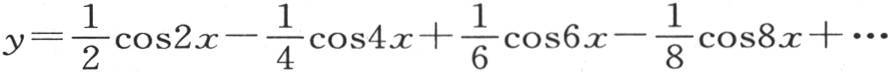 中,我们假定x为零,那么我们得到
中,我们假定x为零,那么我们得到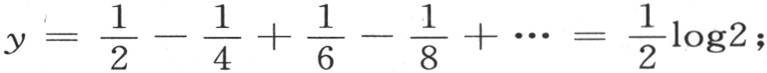 因此
因此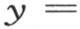
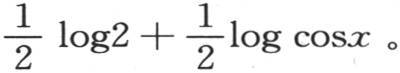 因此我们碰到由欧拉给出的级数
因此我们碰到由欧拉给出的级数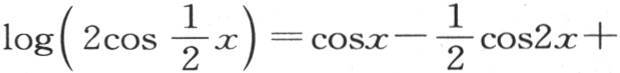

184 对方程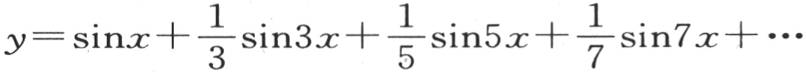 应用同一过程,我们得到下面从未被注意过的级数,
应用同一过程,我们得到下面从未被注意过的级数,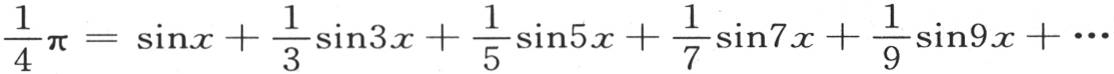 【3】 。
【3】 。
对于所有这些级数,我们应当注意到,只有当变量x包含在某一界限内时,由它们建立的方程才成立。因此,只要变量x不包含在我们所安排的界限之内,函数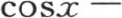
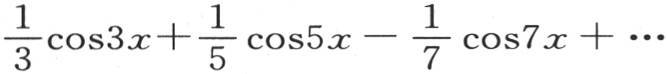 就不等于
就不等于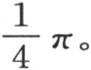 级数
级数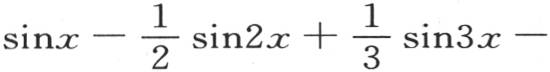
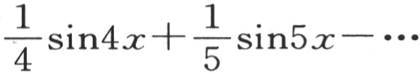 亦如此。只要弧x大于0小于π,这个总是收敛的无穷级数就取值
亦如此。只要弧x大于0小于π,这个总是收敛的无穷级数就取值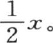 不过,如果这个弧超过π,那么它就不等于
不过,如果这个弧超过π,那么它就不等于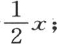 它恰恰取与
它恰恰取与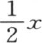 相反的值;因为显然,在从x=π到x=2π的区间内,这个函数以反号取它在前面从x=0到x=π的区间所取的所有值。人们知道这个级数已经很长时间了,但是,用来发现它的这种分析没有指出为什么当变量超过π时这个结果就不成立。
相反的值;因为显然,在从x=π到x=2π的区间内,这个函数以反号取它在前面从x=0到x=π的区间所取的所有值。人们知道这个级数已经很长时间了,但是,用来发现它的这种分析没有指出为什么当变量超过π时这个结果就不成立。
因此,我们应当仔细考查我们所要应用的这种方法,应当寻找每个这样的三角级数所服从的初始界限。
185 为了实现这一点,只需考虑,由那些无穷级数所表示的值只有在完成它们的项的和的极限可以给定的情况下才能精确地知道,就够了;因此,我们应当假定我们只运用这些级数的前几项,并且我们应当找到把余数包含在内的这个界限。
我们把这个注记运用到方程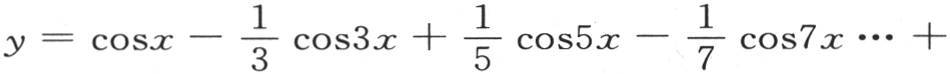
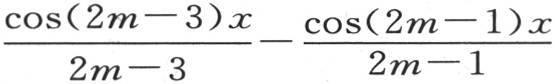 中。它的项数是偶数,用m表示;由此推得方程
中。它的项数是偶数,用m表示;由此推得方程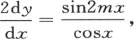 因此,我们可以由分部积分推出y的值。现在,由于u和v是x的函数,所以积分∫uvdx可以分解成由和所期望的一样多的项所组成的一个级数。例如,我们可以写成
因此,我们可以由分部积分推出y的值。现在,由于u和v是x的函数,所以积分∫uvdx可以分解成由和所期望的一样多的项所组成的一个级数。例如,我们可以写成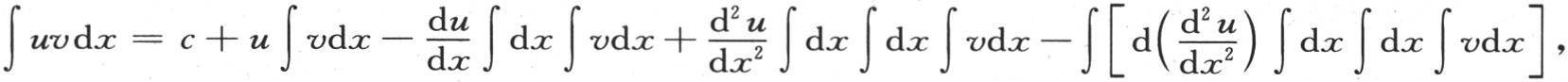 这是一个可通过微分来验证的方程。
这是一个可通过微分来验证的方程。
用v表示sin2mx,用u表示secx,我们得到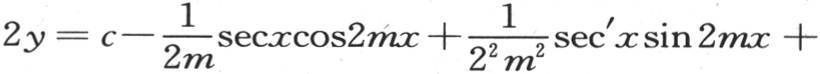

186 现在需要确定把使这个级数完整起来的这个积分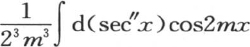 包含在内的那个界限。为了形成这个积分,我们应当对弧x给定从这个积分开始的下限0一直到这个弧的最后的值x的无数值;对于x的每一个这样的值,都应当确定微分d(sec″x)的值和因子cos2mx的值,并且应当加上所有的部分积:现在,可变因子cos2mx必然是一个或正或负的分数;因此,这个积分由这个微分d(sec″x)分别乘以这些分数后所得的这些可变的值的和而组成。这样,当从x=0一直取到x时,这个积分的总值比这些微分d(sec″x)的和要小,反过来取,则它比这个和要大:因为,在第一种情况下,我们是用常量1来代替可变因子cos2mx,在第二种情况下,我们是用-1来代替这个因子:现在,这些微分d(sec″x)的和,或者同样地,从x=0所取的积分∫d(sec″x),是sec″x-sec″0;sec″x是x的某个函数,sec″0是这个函数在弧x为0的假定下所取的值。
包含在内的那个界限。为了形成这个积分,我们应当对弧x给定从这个积分开始的下限0一直到这个弧的最后的值x的无数值;对于x的每一个这样的值,都应当确定微分d(sec″x)的值和因子cos2mx的值,并且应当加上所有的部分积:现在,可变因子cos2mx必然是一个或正或负的分数;因此,这个积分由这个微分d(sec″x)分别乘以这些分数后所得的这些可变的值的和而组成。这样,当从x=0一直取到x时,这个积分的总值比这些微分d(sec″x)的和要小,反过来取,则它比这个和要大:因为,在第一种情况下,我们是用常量1来代替可变因子cos2mx,在第二种情况下,我们是用-1来代替这个因子:现在,这些微分d(sec″x)的和,或者同样地,从x=0所取的积分∫d(sec″x),是sec″x-sec″0;sec″x是x的某个函数,sec″0是这个函数在弧x为0的假定下所取的值。
因此,所求的积分包含在+(sec″x-sec″0)和-(sec″x-sec″0)之间;即,用k表示一个或正或负的未知分数,我们总有∫d(sec″x)cos2mx=k(sec″x-sec″0)。因此我们得到方程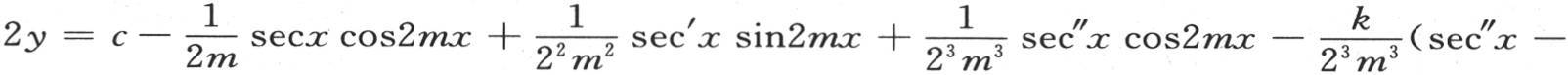
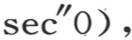 其中量
其中量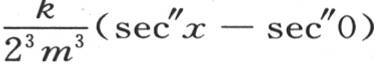 严格地表示这个无穷级数的所有后面那些项的和。
严格地表示这个无穷级数的所有后面那些项的和。
187 如果我们只研究了两项,那么我们有方程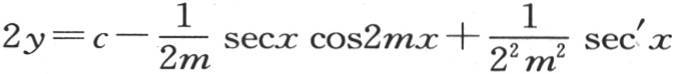
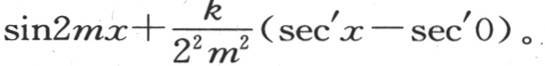 由此得到,我们可以用和我们所希望的一样多的项来展开y值,并精确地表示这个级数的余项;因此我们得到一组方程
由此得到,我们可以用和我们所希望的一样多的项来展开y值,并精确地表示这个级数的余项;因此我们得到一组方程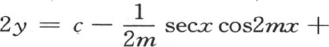
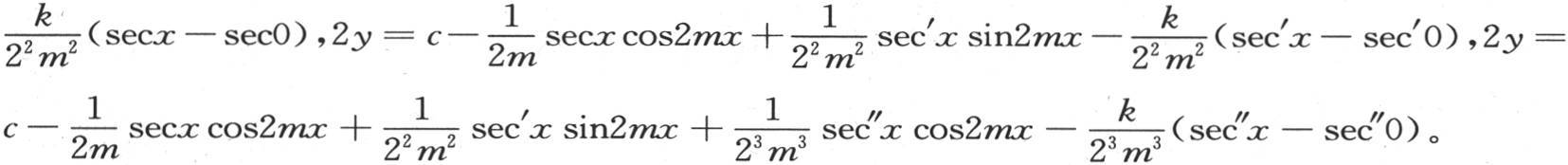
进入这些方程的数k不完全相同,在每个方程中,它表示总包含在1和-1之间的某个量;m等于级数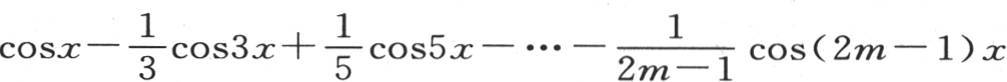 的项数,这个级数的和由y来表示。
的项数,这个级数的和由y来表示。
188 如果给定数m,并且无论这个数有多大,我们都可以像我们所希望的那样严格地确定y值的可变部分,那么,我们就可以应用这些方程。如果数m像假定的那样是无穷的,那么我们只考虑第一个方程;显然,常数后的两项变得愈来愈小;因此,在这种情况下,2y的精确值是常数c;这个常数由在y值中假定x=0而确定,因此我们得到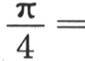
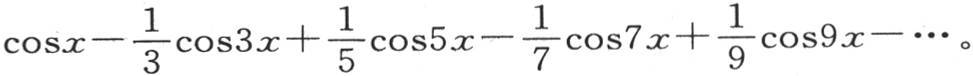
现在容易看出,如果弧x小于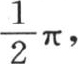 则结果必然成立。事实上,当对这个弧赋予与
则结果必然成立。事实上,当对这个弧赋予与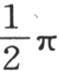 挨得像我们所希望的那样近的一个确定值X时,我们总可以对m给定一个充分大的值,使得使这个级数完整起来的项
挨得像我们所希望的那样近的一个确定值X时,我们总可以对m给定一个充分大的值,使得使这个级数完整起来的项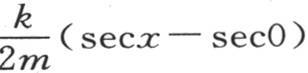 变得小于任一个量;不过,这个结论的正确性以项secx不能取超出所有可能界限的值这样一个事实为基础。由此得到,同一推理不能运用于弧x不小于
变得小于任一个量;不过,这个结论的正确性以项secx不能取超出所有可能界限的值这样一个事实为基础。由此得到,同一推理不能运用于弧x不小于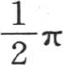 的情况。
的情况。
同样的分析可以运用到表示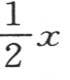 和log cosx的值的级数上去,用这种方法,我们可以给定变量所应当包含在内的界限,以使分析结果不带任何的不确定性;此外,同样这些问题可以用建立在其他原理之上的另一种方法来处理。 【4】
和log cosx的值的级数上去,用这种方法,我们可以给定变量所应当包含在内的界限,以使分析结果不带任何的不确定性;此外,同样这些问题可以用建立在其他原理之上的另一种方法来处理。 【4】
189 一个固体薄片中的固定温度规律的表达式应当以方程
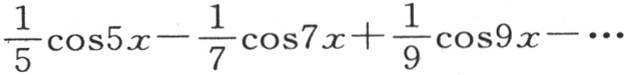 的知识为条件,获得这个方程的更简单的方法如下:
的知识为条件,获得这个方程的更简单的方法如下:
如果两个弦的和等于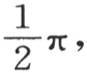 圆周的四分之一,那么它们的正切的积是1;因此,一般地,我们有
圆周的四分之一,那么它们的正切的积是1;因此,一般地,我们有

符号arctanu表示正切为u的弧长,给定那个弧的值的级数是已熟知的;因此我们有下述结果:
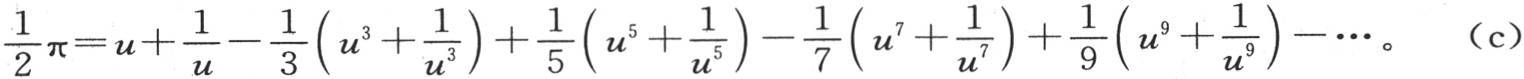
如果现在我们在方程(b)和方程(c)中用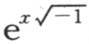 来代替u,则我们有
来代替u,则我们有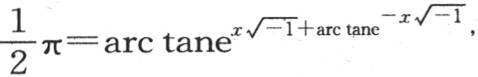 和
和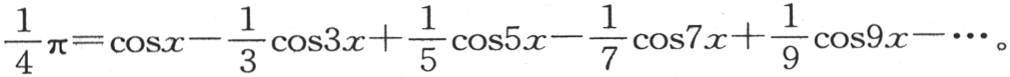
方程(c)的这个级数总是发散的,方程(a)(第180目)的级数总是收敛的;它的值是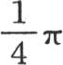 或
或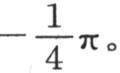
第四节 通 解
190 现在我们可以构造我们所提出的这个问题的全解了;因为,在方程(b)的系数(第169目)确定之后,剩下的就只是代入它们而已,我们有
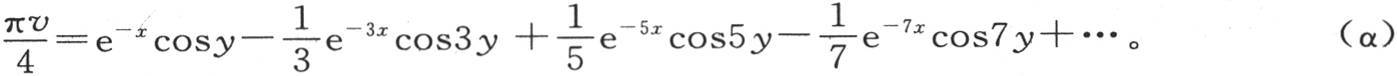
这个v值满足方程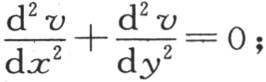 当我们对y给定一个等于
当我们对y给定一个等于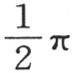 或者是
或者是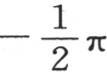 的值时,它变成零;最后,当x为零,y包含在
的值时,它变成零;最后,当x为零,y包含在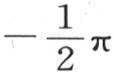 到
到 之间时,它等于1。因此,这个问题的所有物理条件都被满足,无疑,如果我们对这个薄片的每一点都给定方程(α)所确定的温度,同时基底A保持温度1,无穷边B和C保持温度0,那么,这个温度系统中就不可能发生任何变化。
之间时,它等于1。因此,这个问题的所有物理条件都被满足,无疑,如果我们对这个薄片的每一点都给定方程(α)所确定的温度,同时基底A保持温度1,无穷边B和C保持温度0,那么,这个温度系统中就不可能发生任何变化。
191 由于方程(α)的右边呈极其收敛的级数形式,所以总容易从数值上来确定其坐标x和y已知的一点的温度。这个解引出有必要加以注意的各种结果,因为它们也属于这个一般理论。
如果其固定温度被考虑的点m离原点A很远,那么方程(α)右边的值就很接近于等于e-x cosy;如果x是无穷的,则它简化成这一项。
方程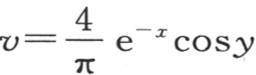 也表示一旦形成便保持不变的这个固体的一个状态;方程
也表示一旦形成便保持不变的这个固体的一个状态;方程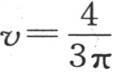
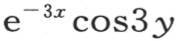 所表示的状态亦如此,一般地,这个级数的每一项都对应着具有这同样性质的一个特殊状态。所有这些局部系统都同时存在于方程(α)所表示的系统之中;它们被叠加,热运动相对于它们的每一个而发生,就像它们单独存在一样。在与这些项的任一个相对应的状态中,基底A的点的固定温度都互不相同,这是未满足这个问题的唯一条件;但是,由所有这些项的和所产生的一般状态则满足这个特殊条件。
所表示的状态亦如此,一般地,这个级数的每一项都对应着具有这同样性质的一个特殊状态。所有这些局部系统都同时存在于方程(α)所表示的系统之中;它们被叠加,热运动相对于它们的每一个而发生,就像它们单独存在一样。在与这些项的任一个相对应的状态中,基底A的点的固定温度都互不相同,这是未满足这个问题的唯一条件;但是,由所有这些项的和所产生的一般状态则满足这个特殊条件。
随着我们考虑其温度的点离原点愈远,热运动就愈不复杂:因为只要距离x充分地大,级数的每一项相对于它前面的项就非常地小,因此,对于受热薄片离原点愈来愈远的那些部分,薄片的状态就明显地由前三项,或者是前两项,或者是仅仅由第一项来表示。
纵坐标计量固定温度v的这个曲面,由许多特殊面的纵坐标相加而成,这些特殊面的方程是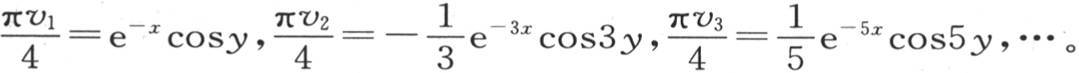
当x无穷时,这些方程的第一个与这个一般曲面重合,它们有一个公共的渐近面。
如果把它们纵坐标的差v-v1 看做是一个曲面的纵坐标,那么当x无穷时,这个面就与方程为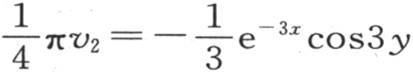 的面重合。这个级数的所有其他项都产生类似的结果。
的面重合。这个级数的所有其他项都产生类似的结果。
如果在原点的截面不是像在实际假定中的那样由平行于y轴的直线围成,而是由两个对称的部分所组成的任一图形,那么我们会再次得到同样的结果。因此显然,特殊值ae-x cosy,be-3x cos3y,ce-5x cos5y,…在这个物理问题中自有它们的来源,并且与热现象有一种必然的联系。它们每一个都表示一个简单的模型,在两个无穷边保持恒温不变的一个矩形薄片中,热按照这种简单模型而形成和传导。这个一般温度系统总是由许多简单系统复合而成,对于它们的和的表达式,只有系数a,b,c,d,…是任意的。
192 方程(α)可以用来确定在其基底受热的矩形薄片中的永恒热运动的一切情况。例如,如果要问热源的消耗怎样,即在一个给定的时间内,流过基底A并且补偿流进冷物质B和C中去的热量的这个热量是多少;那么我们应当认为垂直于y轴的热流量由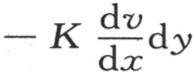 来表示。因此,在时刻dt内流过该轴的一部分dy的热量是
来表示。因此,在时刻dt内流过该轴的一部分dy的热量是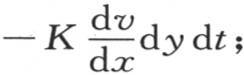 当温度永恒不变时,单位时间内的总热流量是
当温度永恒不变时,单位时间内的总热流量是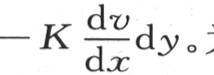 为了确定经过基底的总热量,我们应当在
为了确定经过基底的总热量,我们应当在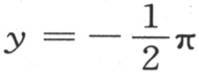 和
和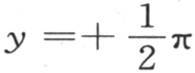 的界限内对这个表达式积分,或者同样地,应当从y=0到
的界限内对这个表达式积分,或者同样地,应当从y=0到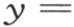
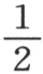 积分,并把这个结果翻一倍。量
积分,并把这个结果翻一倍。量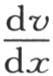 是x和y的一个函数,为了使计算能够适合于与y轴重合的基底A,在这个函数中,应当使x等于0。因此,热源消耗的表达式是
是x和y的一个函数,为了使计算能够适合于与y轴重合的基底A,在这个函数中,应当使x等于0。因此,热源消耗的表达式是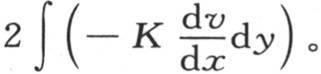 这个积分应当从y=0取到
这个积分应当从y=0取到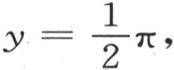 如果在函数
如果在函数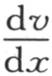 中,假定x不等于0,而是x=x,那么,积分将是x的函数,它表示在单位时间内流过与原点相距x的一个横截边的热量。
中,假定x不等于0,而是x=x,那么,积分将是x的函数,它表示在单位时间内流过与原点相距x的一个横截边的热量。
193 如果我们想确定在单位时间内流过在薄片上所作的平行于边B和C的一条直线的热量,那么我们运用表达式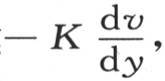 让它乘以所作的直线的基元dx,然后在这条直线的给定边界之间对x积分;因此,积分
让它乘以所作的直线的基元dx,然后在这条直线的给定边界之间对x积分;因此,积分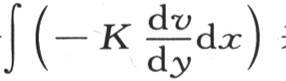 表示有多少热流过这整条直线;如果在这个积分之前或者是之后我们使
表示有多少热流过这整条直线;如果在这个积分之前或者是之后我们使 则我们就可以确定在单位时间内从这个薄片经过无穷边C所逃逸的热量。接着我们可以对最后这个量和热源的消耗进行比较;因为热源必然不断提供流进物质B和C的热。如果这种补偿不是在每一时刻都存在,那么这个温度系统就是变化的。
则我们就可以确定在单位时间内从这个薄片经过无穷边C所逃逸的热量。接着我们可以对最后这个量和热源的消耗进行比较;因为热源必然不断提供流进物质B和C的热。如果这种补偿不是在每一时刻都存在,那么这个温度系统就是变化的。
194 方程(α)给出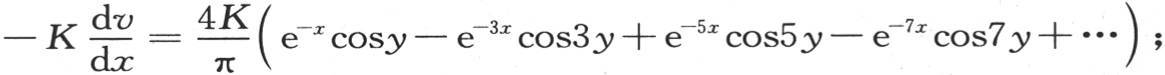 乘以dy,并从y=0积分,我们有
乘以dy,并从y=0积分,我们有
如果令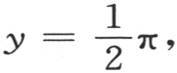 并且使这个积分翻一倍,则我们得到
并且使这个积分翻一倍,则我们得到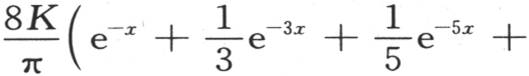
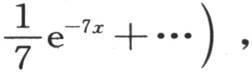 它是在单位时间内经过与基底平行并且与基底相距x的一条直线的热量表达式。
它是在单位时间内经过与基底平行并且与基底相距x的一条直线的热量表达式。
我们从方程(α)还可以推出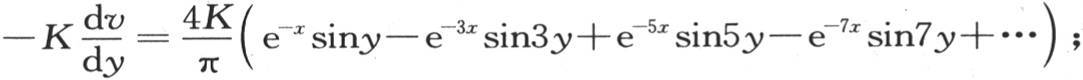 因此,从x=0所取的积分
因此,从x=0所取的积分
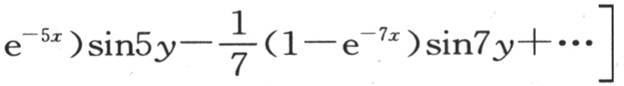 。 【5】
。 【5】
如果从x为无穷时它所取的值中减去这个量,则我们得到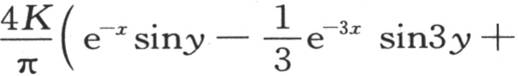
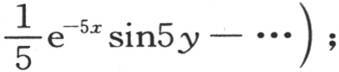 并且,一旦使
并且,一旦使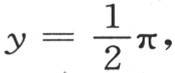 我们就有经过从与原点距离x的点一直到这个薄片的终点的无穷边C的总热量的表达式,即
我们就有经过从与原点距离x的点一直到这个薄片的终点的无穷边C的总热量的表达式,即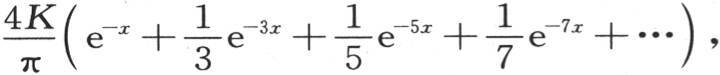 显然,它等于同时通过在这个薄片上在与原点距离x处所作的这条横截线的热量的一半。我们已经注意到,这个结果是这个问题的条件的一个必然推论;如果它不成立,那么这个薄片位于这条横截线以外并且无限延伸的部分,就不能通过它的基底得到等于通过它的两边所失去的热量;因此它不可能保持自己的状态,这与假定矛盾。
显然,它等于同时通过在这个薄片上在与原点距离x处所作的这条横截线的热量的一半。我们已经注意到,这个结果是这个问题的条件的一个必然推论;如果它不成立,那么这个薄片位于这条横截线以外并且无限延伸的部分,就不能通过它的基底得到等于通过它的两边所失去的热量;因此它不可能保持自己的状态,这与假定矛盾。
195 至于热源的消耗,我们由在前一表达式中假定x=0而得到;因此它呈一个无穷值的形式,如果注意到,根据假定,直线A的每一点的温度都取1并且保持1,那么其原因就是显然的:与这个基底很近的平行线也有与1相差无几的温度:因此,所有毗邻的冷物质B和C的这些直线的端点向它们所传导的热量比温度下降为连续的和难以察觉的时要无比地大。在薄片开始的这一部分中,在接近B或者是C的这些端点处,存在一个热瀑(a catarat of heat),或是说一个无穷热流。在距离x变得明显时,这个结果不成立。
196 基底的长曾用π来表示。如果我们对它给定任一值2l,我们则应当用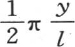 来代替y,也用
来代替y,也用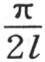 乘x的值时,我们则应当用
乘x的值时,我们则应当用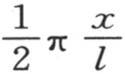 来代替x。用A表示基底的恒温,我们则应当用
来代替x。用A表示基底的恒温,我们则应当用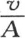 代替v。在方程(α)中作这些代换后,我们有
代替v。在方程(α)中作这些代换后,我们有

这个方程精确地表示包含在两个冰块B和C和一个恒定热源之间的一个无穷矩形棱柱中的永恒温度系统。
197 我们由这个方程或者是从第171目容易看到,热在这个固体中以与原点愈来愈分开、同时指向无穷面B和C的方式传导。与基底截面平行的每个截面由在每一时刻恢复到同一强度的一个热波(a wave of heat)所横切:其强度随截面与原点变得愈远而愈弱。与此类似的运动相对于与两个无穷面平行的任一平面而发生;每一个这样的平面由把它的热传到两侧物质的一个恒波(a constant wave)所横切。
如果我们不是非得要阐明一个有必要确定其原理的全新理论,那么包含在前几目中的推导就不必要了。为此,我们增加下述注记。
198 方程(α)的每一项只对应于可存在于底部受热、两个无穷边保持一恒温的矩形薄片中的一个特殊温度系统。因此,当基底的点有由cosy所表示的固定温度时,方程v=e-x cosy就表示这些永恒温度。现在我们设想这个受热薄片是在所有方向上都无限延伸的一个薄片的一部分,用x和y来表示这个平面任一点的坐标,用v来表示该点的温度,我们可对这整个平面运用方程v=e-x cosy;由此,边B和C得到恒温0;但是邻接部分BB和CC的温度则不同;它们得到并保持更低的温度。基底A在每一点有由cosy所表示的永恒温度,邻接部分AA有更高的温度。如果我们作其纵坐标等于这个平面每一点的永恒温度的一个曲面,并且如果它被经过直线A或者是与直线A平行的一个垂直平面所截,那么截线形式就是一条三角曲线的形式,它的纵坐标表示这个无穷的和周期的余弦级数。如果该曲面被与x轴平行的一个垂直平面所截,那么截线形式就是通过其全长的对数曲线的形式。
199 由此可见这一分析怎样满足假定基底温度等于cosy,两边B和C的温度等于0的这两个条件。在我们表示这两个条件时,我们事实上是在解决下述问题:如果这个受热薄片构成一个无穷平面的一部分,那么,为使这个系统能自永恒,并使这个无穷矩形的固定温度能成为这个假定所给定的温度,这个平面的所有点的温度应当是怎样的?
我们在前一部分中曾经假定某些外因使这个矩形固体的三个面一个保持1度,另两个保持0度。这种效应可以以不同的方式来表示;不过,适合于这个研究的假定在于把这个棱柱看做是其所有尺寸都为无穷的一个固体的一部分,在于确定包围这个棱柱的物质的温度,因此,我们总可以保持与这个面有关的这两个条件。
200 为了确定在极面A保持1度,两个无穷边保持0度的一个矩形薄片的永恒温度系统,我们可以考虑温度从已知的初始状态到作为这个问题目的的固定状态所经历的变化。因此,我们可以确定这个固体相对于所有时间值的变化状态,然后假定时间值是无穷的。
我们所采用的方法是不同的,它更直接地通向终极状态的表达式,因为它以这个状态的一个独特性质为基础。我们现在要表明,除了我们所表示的解以外,这个问题不可能有其他的解。证明由下述命题得出。
201 如果我们对一个无穷矩形薄片的所有点给定由方程(α)所表示的温度,如果我们在两边保持固定温度0,同时基底A受到使这条直线A的所有点都保持固定温度1的一个热源的作用;那么,这个固体的状态不可能发生任何变化。事实上,由于方程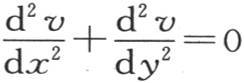 被满足,所以显然(第170目),确定每个分子温度的热量既不能增加也不能减少。
被满足,所以显然(第170目),确定每个分子温度的热量既不能增加也不能减少。
在这同一固体的不同点得到由方程(α)或者是v=φ(x,y)所表示的温度后,假定边A不是保持1度,而是给定和两条直线B和C一样的固定温度0,那么保留在薄片BAC中的热将流过三条边A,B,C,由假定,它得不到补充,因此温度将不断降低,它们最后的和公共的值是零。这个结果是显然的,因为,根据建立方程(α)的方法,离原点A无穷远的点只有无穷小的温度。
如果这个温度系统不是v=φ(x,y),而是v=-φ(x,y);则同一作用就在反方向上发生;即所有这些初始负温度不断变化,并且愈来愈趋近于它们的终极值0,同时三条边A,B,C保持0度不变。
202 设v=f(x,y)是表示这个薄片BAC中的这些点的初始温度的一个已知方程,该薄片基底A保持1度,同时边B和C保持0度。
设v=F(x,y)是表示一个固体薄片BAC中每一点的初始温度的另一个已知方程,该固体薄片完全与前面的一样,只是它的三条边B,A,C都保持0度。
假定在第一个固体中,继终极状态之后的变化状态由方程v=φ(x,y,t)来确定,t表示历经时间,方程v=Φ(x,y,t)确定第二个固体的变化状态,第二个固体的初始温度是F(x,y)。
最后,假定和前两个相同的第三个固体:设v=f(x,y)+F(x,y)是表示它初始状态的方程,设基底A的恒温是1,两条边B和C的恒温均为0。
我们继而表明,第三个固体的变化状态由方程v=φ(x,y,t)+Φ(x,y,t)来表示。
事实上,第三个固体的一点m的温度是变化的,因为其体积由M表示的那个分子得到或者是失去一定的热量△。在时刻dt内,温度增量是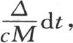 系数c表示相对于体积的比热。同一点的温度变化在第一个固体中是
系数c表示相对于体积的比热。同一点的温度变化在第一个固体中是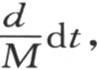 在第二个固体中是
在第二个固体中是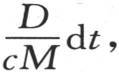 字母d和D表示这个分子因所有相邻分子的作用而得到的或正或负的热量。现在容易看出,∆等于d+D。对这一点的证明只需考虑这一点m从或者是属于这一薄片的内点、或者是属于围住这一薄片的几条边的另一点m′所得到的热量,就够了。
字母d和D表示这个分子因所有相邻分子的作用而得到的或正或负的热量。现在容易看出,∆等于d+D。对这一点的证明只需考虑这一点m从或者是属于这一薄片的内点、或者是属于围住这一薄片的几条边的另一点m′所得到的热量,就够了。
点m1 的初始温度由f1 来表示,它在时刻dt内向分子m传送由q1 (f1 -f)所表示的热量,因子q1 表示这两个分子之间的距离的某个函数。因此,m所得到的全部热量是∑q1 (f1 -f)dt,符号∑表示通过考虑作用于m的其他点m2 ,m3 ,m4 ,…所得到的所有项的和;即用q2 ,f2 ,或q3 ,f3 ,或q4 ,f4 ,…代替q1 ,f1 。同样,我们会发现∑q1 (F1 -F)是由第二个固体的同一点m所得到的全部热量的表达式;因子q1 与项∑q1 (f1 -f)中的一样,因为,这两个固体由相同的物质组成,并且点的位置相同,这样,我们有d=∑q1 (f1 -f)dt和D=∑q1 (F1 -F)dt。由同一原因,我们可以得到∆=∑q1 [f1 +F1 -(f+F)]dt;因此∆=d+D和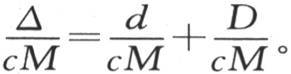
由此得到,第三个固体的分子m在时刻dt内得到与同一点在前两个固体中所得到的两个增量的和相等的温度增量。因此,在第一时刻末,初始假定仍然成立,因为第三个固体的任一分子都有与在其他两个固体中所有的温度的和相等的温度。因此,这同一关系在每一时刻开始时都存在。即,第三个固体的变化状态总可以由方程v=φ(x,y,t)+Φ(x,y,t)来表示。
203 前述命题可应用于与均匀的或变化的热运动有关的一切问题。它表明,这个运动总可以分解成几个别的运动,其中每一个都分别起作用,就像它们单独存在一样。这种简单作用的叠加是热理论的基本原理之一。在本研究中,我们正是用一般方程的性质来表示它,并根据热传导原理而推出它的来源的。
现在设v=φ(x,y)是方程(α),它表示在基底A受热并且边B和C保持0度不变的固体薄片BAC的永恒状态;由假定,这个薄片的初始状态是这样的:除基底A的那些点的温度是1外,它所有其他点的温度都是0。这样,我们可以把这个初始状态看做是由两个其他状态所组成的,在这两个状态的第一个中,初始温度是-φ(x,y),三条边均保持0度,在第二个中,初始温度是+φ(x,y),两条边B和C保持0度,基底A保持1度;这两个状态的叠加等于假定的初始状态。这样,剩下的只需考查在这两个部分状态的每一个中的热运动就够了。现在,在第二个状态中,温度系统不可能经历任何变化;在第一个状态中,我们已经在第201目中注意到,温度将连续变化,并且最后以0结束。因此,严格意义上的终极状态,是由方程v=φ(x,y)或者是方程(α)所表示的状态。
如果这个状态一开始就形成,那么它将自行存在,并且,它就是我们用以确定这个状态的性质。如果我们假定这个固体薄片处在另一个初始状态中,那么,后一状态与固定状态的差形成一个部分状态,这个部分状态隐隐地消失。经过相当长的时间之后,这个差接近于零,固定温度系统不发生任何变化。因此,变化温度愈来愈收敛于与初始热无关的终极状态。
204 由此我们看到,终极状态是唯一的;因为,若设想第二个终极状态,则第二个和第一个的差则形成一个部分状态,虽然三条边A,B,C保持0度,但是这一个部分状态仍应是自存在的。现在类似地,如果我们假定与从原点A所流过的热源无关的另一个热源;那么这个最后效应不可能发生;此外,这个假定不是我们已经处理过的问题的假定,在我们的问题中,初始温度为0。显然,离原点很远的部分只能得到极小的温度。
由于必须确定的终极状态是唯一的,所以由此得到,所提出的这个问题只有等于方程(α)的解,不可能有别的解。我们可以对这个结果给出另一种形式,不过,我们既不可能扩大也不可能缩小这个解而不改变它的精确性。
我们在本章所阐明的这个方法首先在于得出符合这个问题的几个很简单的特殊值,在于使这个解更一般,从而使v或者是φ(x,y)能满足三个条件,即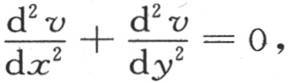
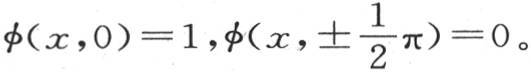
显然,我们也可以按相反的次序进行,所得到的解必然和前面的一样。我们不打算讨论这些细节,因为一旦得到解,这些细节就很容易补充。我们只在下一节为函数φ(x,y)给出一个值得注意的表达式,函数φ(x,y)的值在方程(α)中以一个收敛级数展开。
第五节 解的结果的有限表达式
205 前述解应当根据方程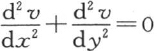 【6】 的积分推出,该方程的任意函数符号内包含有虚量。此处我们只注意积分
【6】 的积分推出,该方程的任意函数符号内包含有虚量。此处我们只注意积分
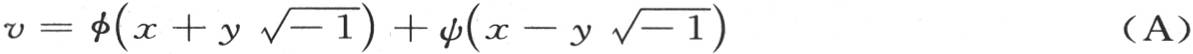
与方程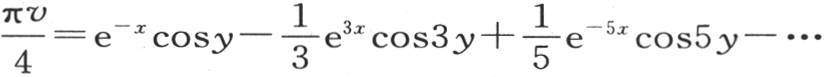 所给定的v值有一个明显的关系。
所给定的v值有一个明显的关系。
事实上,用余弦的虚式代替余弦,我们有

第一个级数是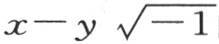 的函数,第二个级数是
的函数,第二个级数是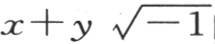 的相同函数。
的相同函数。
比较这些级数和z的正切函数中arc tanz的已知展开式,我们立即看到,第一个级数是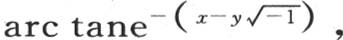 第二个是
第二个是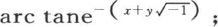 因此,方程(α)有有限形式
因此,方程(α)有有限形式
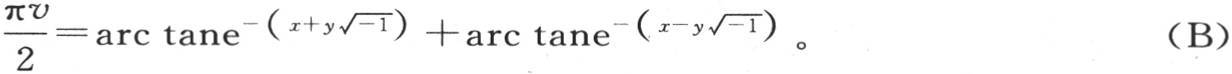
在这个形式中,它与通积分

相一致。函数φ(z)是arc tane-x ,函数ψ(z)亦如此。
如果在方程(B)中,我们用p表示右边第一项,用q表示第二项,那么我们有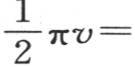
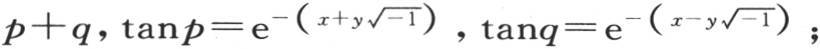 因此
因此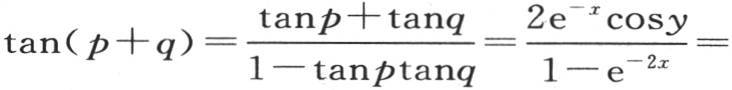
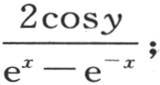 这样,我们推出方程
这样,我们推出方程

这是我们可以据以表述该问题的解的最简形式。
206 v或φ(x,y)的这个值满足与固体边界有关的条件,即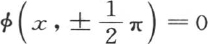 和φ(0,y)=1;它也满足一般方程
和φ(0,y)=1;它也满足一般方程 因为方程(C)是方程(B)的一个变换。因此它严格表示这个永恒的温度系统;由于那个状态是唯一的,所以,不可能有更一般或更严格的任何其他的解。
因为方程(C)是方程(B)的一个变换。因此它严格表示这个永恒的温度系统;由于那个状态是唯一的,所以,不可能有更一般或更严格的任何其他的解。
当未知数v,x,y中有两个是已知的时,由表,方程(C)提供另一个未知数的值;它非常清楚地指明其纵坐标是这个固体薄片一个已知点的永恒温度的那个曲面的性质。最后,我们由这同一方程得到计量热在两个垂直方向上所流过的速度的微分系数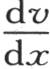 和
和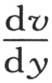 的值,我们因而知道在任何其他方向的热流量的值。
的值,我们因而知道在任何其他方向的热流量的值。
因此,这两个系数被表示成 【7】 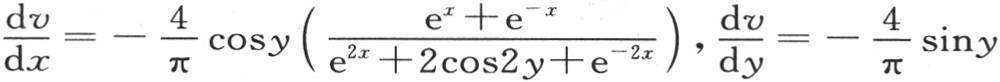
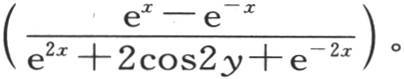
我们可以注意到,在第194目中,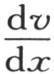 的值,以及
的值,以及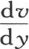 的值,是由无穷级数给出的,用虚数幂代替三角函数的值,我们很容易得到这些级数的和。
的值,是由无穷级数给出的,用虚数幂代替三角函数的值,我们很容易得到这些级数的和。
我们现在所处理的这个问题,是我们在热的理论中,或更准确地说,在需要运用分析的这个理论的那部分中所解决的第一个问题。不管我们是利用三角函数表,还是利用收敛级数,它都提供很简单的数值应用,它严格表示热运动的一切情况。我们现在转到更一般的考虑上来。
第六节 任意函数的三角级数展开
207 矩形固体中的热传导问题已经导出方程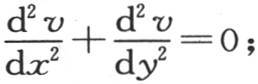 如果假定这个固体的某个面的所有点有相同的温度,那么我们应当确定级数acosx+bcos3x+ccos5x+dcos7x+…的系数a,b,c,d,…,从而使得只要弧x包含在
如果假定这个固体的某个面的所有点有相同的温度,那么我们应当确定级数acosx+bcos3x+ccos5x+dcos7x+…的系数a,b,c,d,…,从而使得只要弧x包含在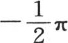 到
到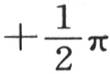 之间,这个函数的值就等于一个常数。虽然我们刚才已经给出这些系数的值;但是在这当中我们只处理了一个更一般的问题的一个个别情况,这个更一般的问题在于以多重弧的正弦或余弦的无穷级数来展开任意一个函数。该问题与偏微分方程理论相联系,并且,自那种分析产生以来,人们就一直试图解决它。为了对热传导方程进行适当积分,我们有必要解决这个问题。我们现在开始解释这个解。
之间,这个函数的值就等于一个常数。虽然我们刚才已经给出这些系数的值;但是在这当中我们只处理了一个更一般的问题的一个个别情况,这个更一般的问题在于以多重弧的正弦或余弦的无穷级数来展开任意一个函数。该问题与偏微分方程理论相联系,并且,自那种分析产生以来,人们就一直试图解决它。为了对热传导方程进行适当积分,我们有必要解决这个问题。我们现在开始解释这个解。
首先,我们考虑需要把其展开式只含变量奇数幂的函数化成一个多重弧的正弦级数的情况。用φ(x)表示这样一个函数,我们则设置方程φ(x)=asinx+bsin2x+csin3x+dsin4x+…,在这个方程中,需要确定系数a,b,c,d,…的值。我们先把方程写成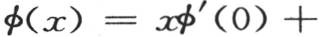
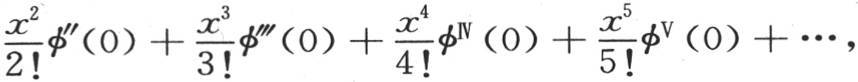 其中
其中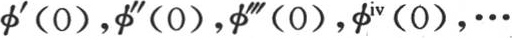 表示系数
表示系数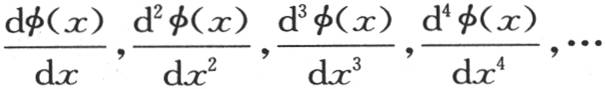 在我们假定其中x=0时所取的值。因此,根据x的幂,用方程
在我们假定其中x=0时所取的值。因此,根据x的幂,用方程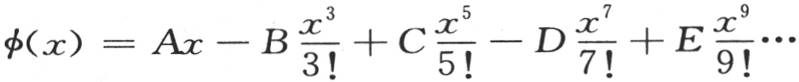 来表示这个展开式,我们有
来表示这个展开式,我们有

如果我们现在比较前述方程和方程φ(x)=asinx+bsin2x+csin3x+dsin4x+esin5x+…,那么,以x的幂展开右边,我们有方程
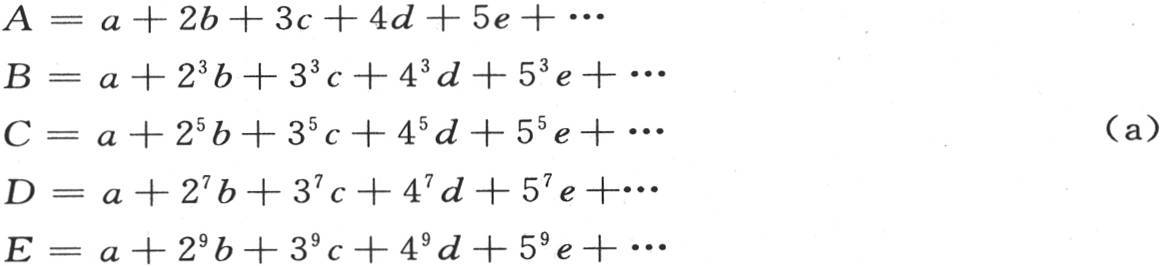
这些方程用来求出数目无穷的系数a,b,c,d,e,…。为了确定它们,我们首先把未知数的数目看做是有限的,并且等于m;因此,我们删去前m个方程之后的所有方程,并且从每个方程中略去右边我们保留的前m项之后的所有项。由于总数m被给定,所以系数a,b,c,d,e,…已经固定了由消元所能得到的那些值。如果方程和未知数的数目一个一个地增大,那么同一个量可以得到不同的值。因此,这些系数的值随我们增加应该确定它们的系数和未知数的数目而变化。我们需要求出在方程的数目增加时,未知数的值所不断收敛的极限。这些极限是满足前面那些方程的未知数在其数目无限时的真正的值。
208 这样,我们依次考虑这样一些情况,在这些情况中,我们不得不用一个方程确定一个未知数,用两个方程确定两个未知数,用三个方程确定三个未知数,以此类推,以至无穷。
与系数的值必定从中导出的那些方程类似,假定我们把不同的方程组表示如下:
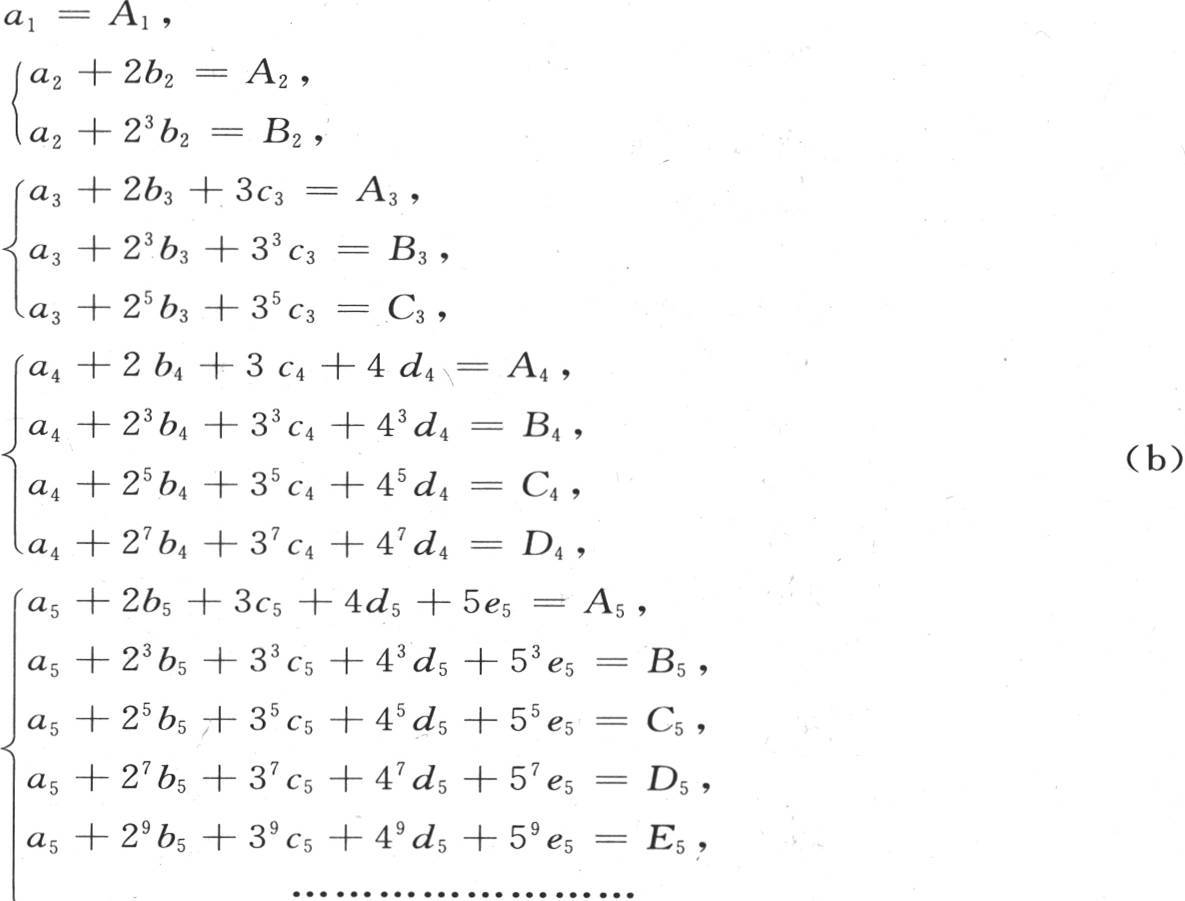
如果现在我们用包含A5 ,B5 ,C5 ,D5 ,E5 ,…的五个方程消去最后的未知数e5 ,那么我们得到

在前面由四个方程组成的方程组中,
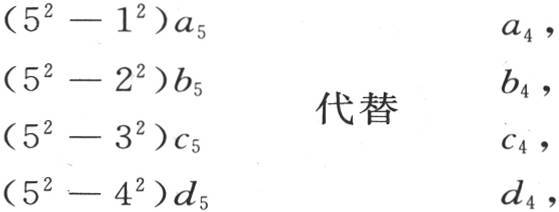
并且用

我们就可以从中推导出上面这四个方程。
由类似的代换,我们总可以从对应于m个未知数的情况过渡到对应于m+1个未知数的情况。依次写出对应于这些情况中某一种的各个量之间的所有关系,和对应于随后那种情况的各个量之间的所有关系,我们就有
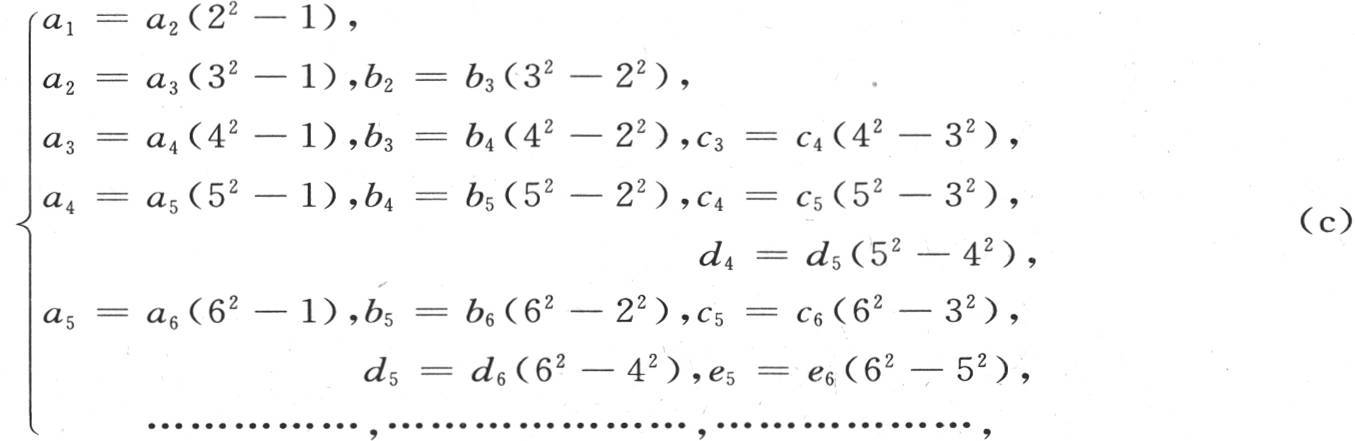
我们还有
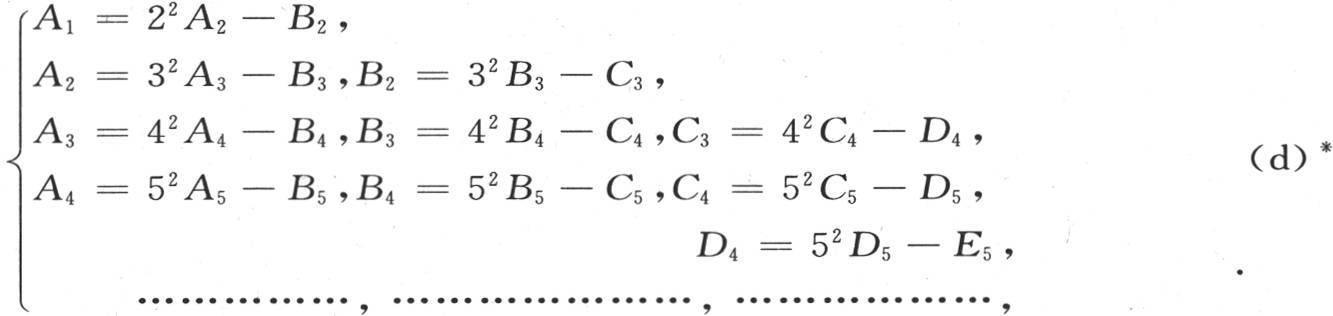
* 在英文版中,方程组(d)中各行中的数没有平方,但英译者在脚注中指出:各行中的数应当平方。这说明原法文版中各数是没有平方的。但是,法文《文集》版中有平方。因此,现直接加上。——汉译者
由方程(c)我们得到,一旦用a,b,c,d,e,……表示其数目无限的这些未知数,我们就肯定有
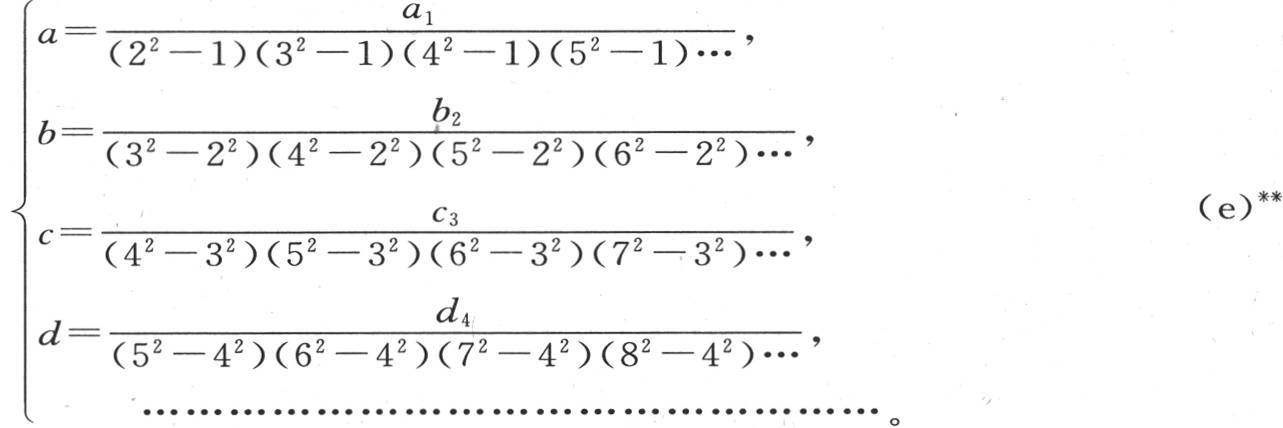
** 法文《文集》本的编者加斯东·达布在此给了一个脚注,他提出了一种方法,来克服分母无穷大的困难:
这些乘积表明这些分母是无穷大的,因而不能引进到这些推理中去。在已经有了很多异议的一种方法中,这就是一个更大的困难。我们通过下述方式可以避免这一困难。
用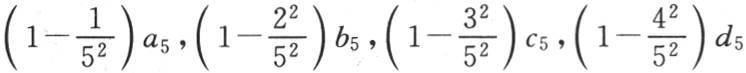 来代替a4 ,b4 ,c4 ,d4 ,并且用
来代替a4 ,b4 ,c4 ,d4 ,并且用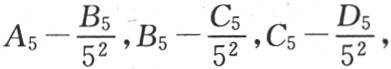
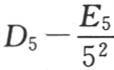 来代替A4 ,B4 ,C4 ,D4 ,我们就能用前页中的那四个方程推出组成前面那个方程组的那些方程,这时,前页的那些方程组有下述形式:
来代替A4 ,B4 ,C4 ,D4 ,我们就能用前页中的那四个方程推出组成前面那个方程组的那些方程,这时,前页的那些方程组有下述形式:
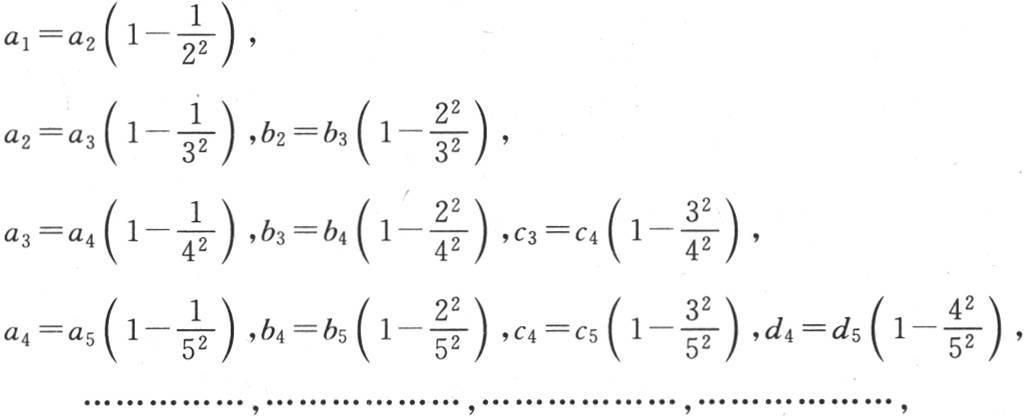
我们还有

因此,

至于由下一目所给定的不同的A值,它们变成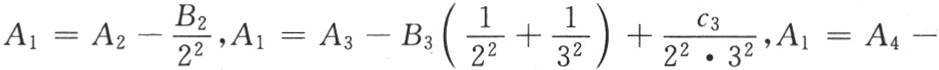
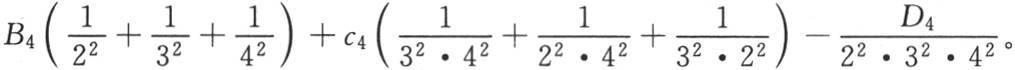
我们可以对A2 ,B2 ,A3 ,…进行同样的运算,因此,这部分的推理是完全重复的。——汉译者
209 这样,剩下的就是确定a1 ,b2 ,c3 ,d4 ,e5 ,…的值;第一个由A1 进入其中的一个方程来给定;第二个由A2 ,B2 进入其中的两个方程给定;第三个由A3 ,B3 ,C3 进入其中的三个方程给定;以此类推。由此得到,如果我们知道A1 ;A2 ,B2 ;A3 ,B3 ,C3 ;A4 ,B4 ,C4 ,D4 ;…的值,那么,通过解一个方程,我们就不难得到a1 ,解两个方程,就得到a2 ,b2 ,解三个方程,就得到a3 ,b3 ,c3 ,…:在此之后,我们就可以确定a,b,c,d,e,…。这样,就需要用方程(d)来计算A1 ;A2 ,B2 ;A3 ,B3 ,C3 ;A4 ,B4 ,C4 ,D4 ;A5 ,B5 ,C5 ,D5 ,E5 ;…的值。第一,我们根据A2 和B2 得到A1 的值;第二,通过两个代换,我们由A3 ,B3 ,C3 得到这个A1 的值;第三,通过三个代换,我们由A4 ,B4 ,C4 ,D4 得到同一个A1 的值,…。A1 的逐个值是
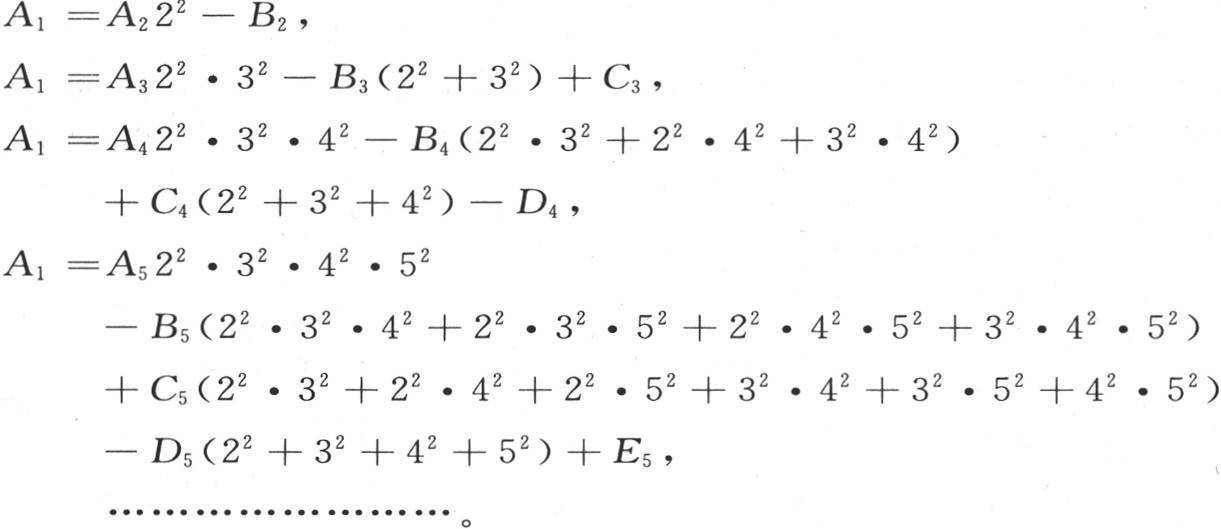
我们已经注意到其中的规律。这些值的最后一个,是我们要确定的值,它包含带有无穷下标的量A,B,C,D,E,…,这些量是已知的;它们和进入方程(a)的那些量相同。
把A1 的终极值除以无穷积22 ·32 ·42 ·52 ·62 …,则我们有

这些数值系数是分数 在去掉第一个分数
在去掉第一个分数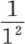 之后的不同组合所形成的积的和。如果我们用P1 ,Q1 ,R1 ,S1 ,T1 …来表示这些积的各个和,并且如果我们运用方程(e)的第一个方程和方程(b)的第一个方程,那么,为了表示第一个系数a的值,我们有方程
之后的不同组合所形成的积的和。如果我们用P1 ,Q1 ,R1 ,S1 ,T1 …来表示这些积的各个和,并且如果我们运用方程(e)的第一个方程和方程(b)的第一个方程,那么,为了表示第一个系数a的值,我们有方程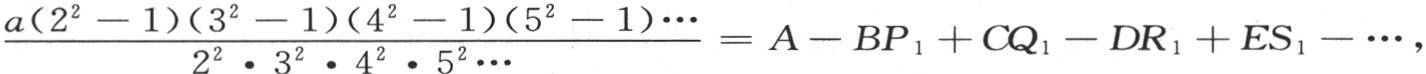 正如我们在下面将要看到的,现在容易确定量P1 ,Q1 ,R1 ,S1 ,T1 ,…;因此,第一个系数a就完全变成已知数了。
正如我们在下面将要看到的,现在容易确定量P1 ,Q1 ,R1 ,S1 ,T1 ,…;因此,第一个系数a就完全变成已知数了。
210 我们现在应当继续研究后面的系数b,c,d,e,…,根据方程(e),它们依赖于量b2 ,c3 ,d4 ,e5 ,…。为此,我们运用方程(b),第一个方程已经用来求a1 的值,后两个给出b2 的值,接下去的三个给出c3 的值,再后面的四个给出d4 的值,…。
一旦完成这个计算,通过对这些方程的简单观察,我们就得到b2 ,c3 ,d4 ,…的下述结果:
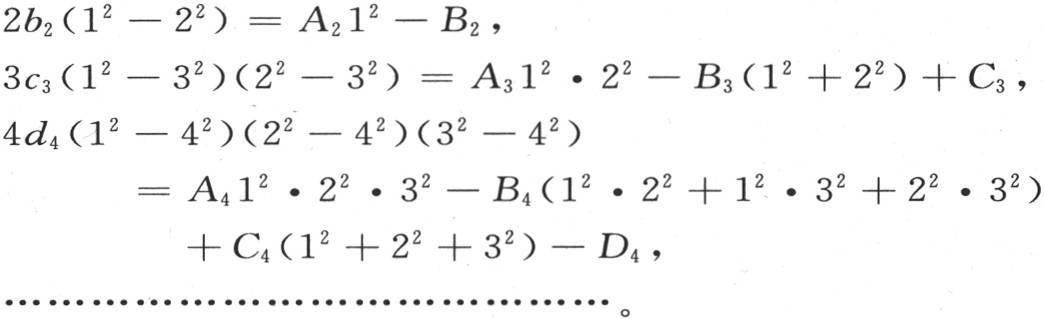
我们不难看出这些方程所遵循的规律;剩下的只是确定量A2 ,B2 ;A3 ,B3 ,C3 ;A4 ,B4 ,C4 ,D4 …。
现在量A2 ,B2 可以用A3 ,B3 ,C3 来表示,而后者可以用A4 ,B4 ,C4 ,D4 表示。为此,只需完成由方程(d)所指明的代换就够了;这逐次的变换简化前面那些方程的右边,以致最后只包含带有无穷下标的A,B,C,D…,也就是说,只包含进入方程(a)的已知量A,B,C,D…;这些系数变成可以通过组合1,2,3,4,5,直至无穷的这些数的平方而得到的不同积。我们只需注意,这些平方的第一个12 不进入a1 的值的系数;第二个22 不进入b2 的值的系数;第三个32 只从那些用来形成c3 的值的系数中略去;余此类推,以至无穷。这样,对于b2 ,c3 ,d4 ,e5 ,…的值,因而对于b,c,d,e,…的值,我们有与我们在上面对第一个系数a1 所得到的完全类似的结果。
211 如果现在我们用P2 ,Q2 ,R2 ,S2 ,…来表示量

这些量由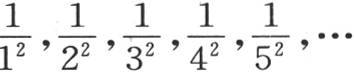 以至无穷的这些分数组合所形成。为了确定b2 的值,在这些分数中略去
以至无穷的这些分数组合所形成。为了确定b2 的值,在这些分数中略去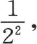 我们就有方程
我们就有方程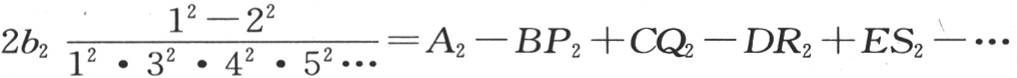 。 【8】
。 【8】
一般地,在 以至无穷的所有分数中刚好删去
以至无穷的所有分数中刚好删去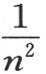 以后,用Pn ,Qn ,Rn ,Sn ,…来表示以组合这些分数所得的积的和;我们通常就有确定量a1 ,b2 ,c3 ,d4 ,e5 ,…的下述方程 【9】 :
以后,用Pn ,Qn ,Rn ,Sn ,…来表示以组合这些分数所得的积的和;我们通常就有确定量a1 ,b2 ,c3 ,d4 ,e5 ,…的下述方程 【9】 :

212 如果我们现在考查给出系数a,b,c,d,…的值的方程(e),那么我们有下述结果:

注意,为了使分子和分母各自的两个自然数序列完整无缺所需要的那些因子,我们会看到,第一个方程中的分式约简为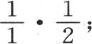 第二个方程中的分式约简为
第二个方程中的分式约简为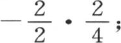 第三个中的,约简为
第三个中的,约简为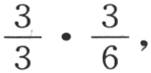 第四个中,
第四个中,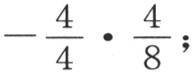 因此,乘以a,2b,3c,4d,…的这些积,交替地是
因此,乘以a,2b,3c,4d,…的这些积,交替地是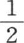 和
和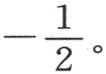 这样,只需要求P1 ,Q1 ,R1 ,S1 ;P2 ,Q2 ,R2 ,S2 ;P3 ,Q3 ,R3 ,S3 ;…的值就够了。
这样,只需要求P1 ,Q1 ,R1 ,S1 ;P2 ,Q2 ,R2 ,S2 ;P3 ,Q3 ,R3 ,S3 ;…的值就够了。
为了得到这些值,我们可以注意,我们能使这些值随量P,Q,R,S,T,…的值而定,量P,Q,R,S,T,…表示可由分数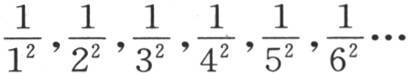 不删去任何一个而组成的不同的积。
不删去任何一个而组成的不同的积。
对于上面这些积,它们的值由表示正弦展开式的级数给出。因此我们用P,Q,R,S,…表示级数
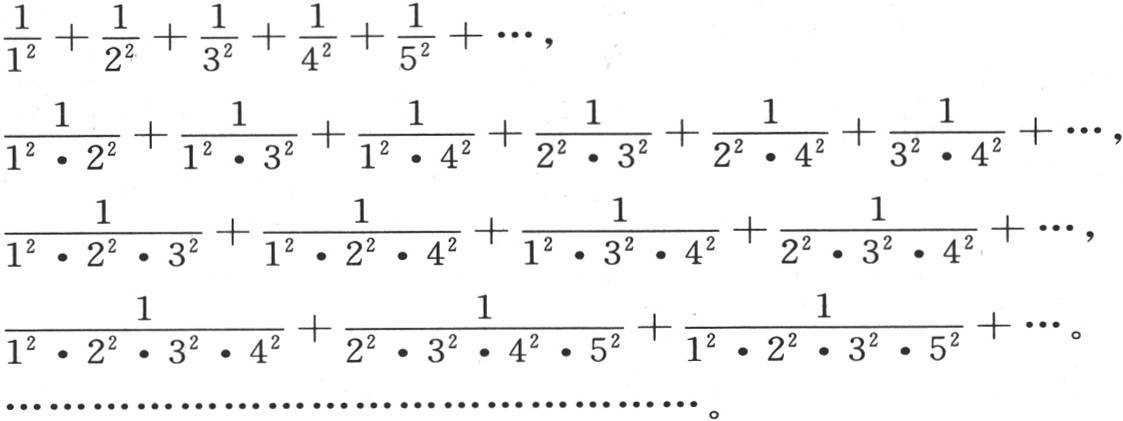
级数 提供量P,Q,R,S,…的值。事实上,由于正弦的值由方程
提供量P,Q,R,S,…的值。事实上,由于正弦的值由方程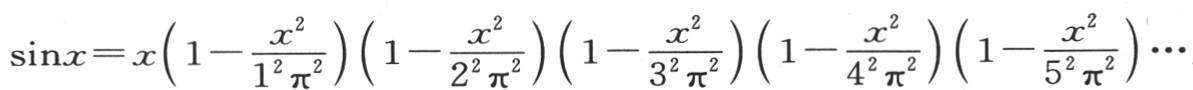 来表示,所以我们有
来表示,所以我们有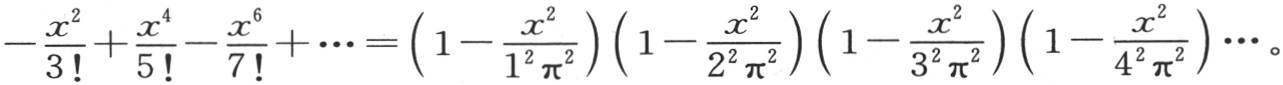 因此我们立即得到
因此我们立即得到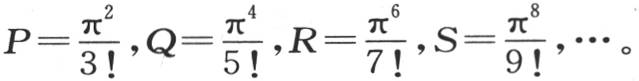
213 现在假定Pn ,Qn ,Rn ,Sn ,…表示可以分数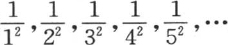 所形成的不同积的和,
所形成的不同积的和,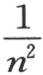 已从这些分数中去掉,n为任一整数;我们需要由P,Q,R,S,…来确定Pn ,Qn ,Rn ,Sn ,…。如果我们用1-qPn +q2 Qn -q3 Rn +q4 Sn -…来表示因子
已从这些分数中去掉,n为任一整数;我们需要由P,Q,R,S,…来确定Pn ,Qn ,Rn ,Sn ,…。如果我们用1-qPn +q2 Qn -q3 Rn +q4 Sn -…来表示因子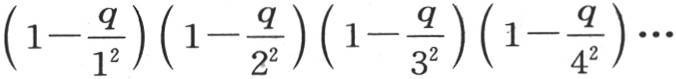 的积,在上述因子中只有因子
的积,在上述因子中只有因子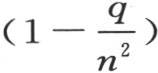 被略去;那么由此得到,只要用
被略去;那么由此得到,只要用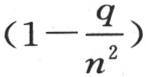 乘量1-qPn +q2 Qn -q3 Rn +q4 Sn -…,我们就得到1-qP+q2 Q-q3 R+q4 S-…。
乘量1-qPn +q2 Qn -q3 Rn +q4 Sn -…,我们就得到1-qP+q2 Q-q3 R+q4 S-…。
这个比较给出下述关系: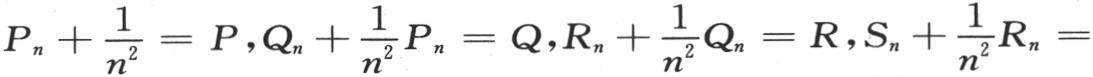
 或者是
或者是
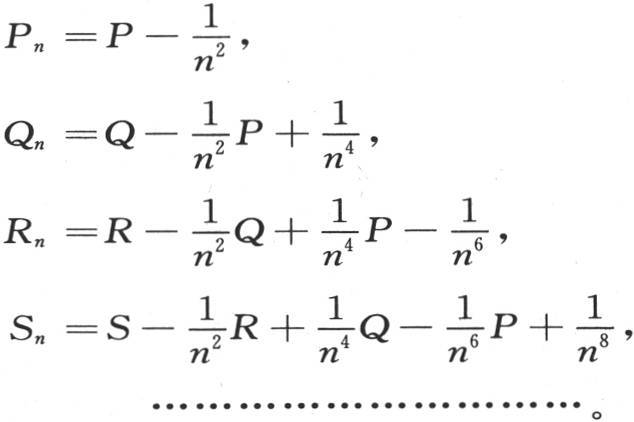
运用P,Q,R,S等的已知值,并依次取n等于1,2,3,4,5,…,我们就有P1 ,Q1 ,R1 ,S1 ,…的值;P2 ,Q2 ,R2 ,S2 ,…的值;P3 ,Q3 ,R3 ,S3 ,…的值。
214 由上述理论得到:从方程a+2b+3c+4d+5e+…=A,a+23 b+33 c+43 d+53 e+…=B,a+25 b+35 c+45 d+55 e+…=C,a+27 b+37 c+47 d+57 e+…=D,a+29 b +39 c+49 d+59 e+…=E,所推出的a,b,c,d,e,…的值因而表示成, 【10】
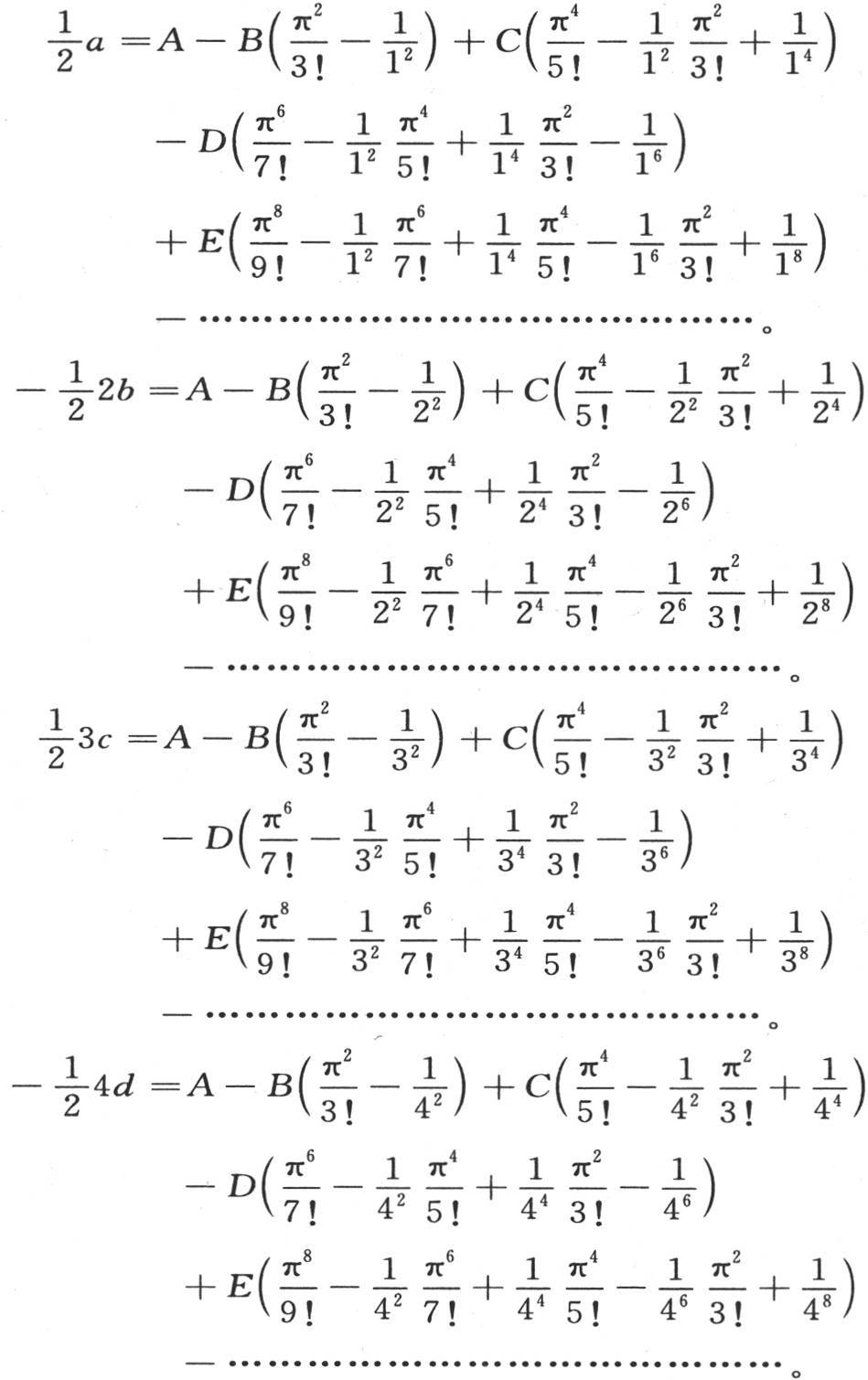
215 知道了a,b,c,d,e,…的值,我们就可以在所提出的方程
φ(x)=asinx+bsin2x+csin3x+dsin4x+esin5x+…
中替换它们,同样,不用量A,B,C,D,E,…,而代之以它们的值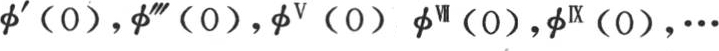 我们就有一般方程
我们就有一般方程
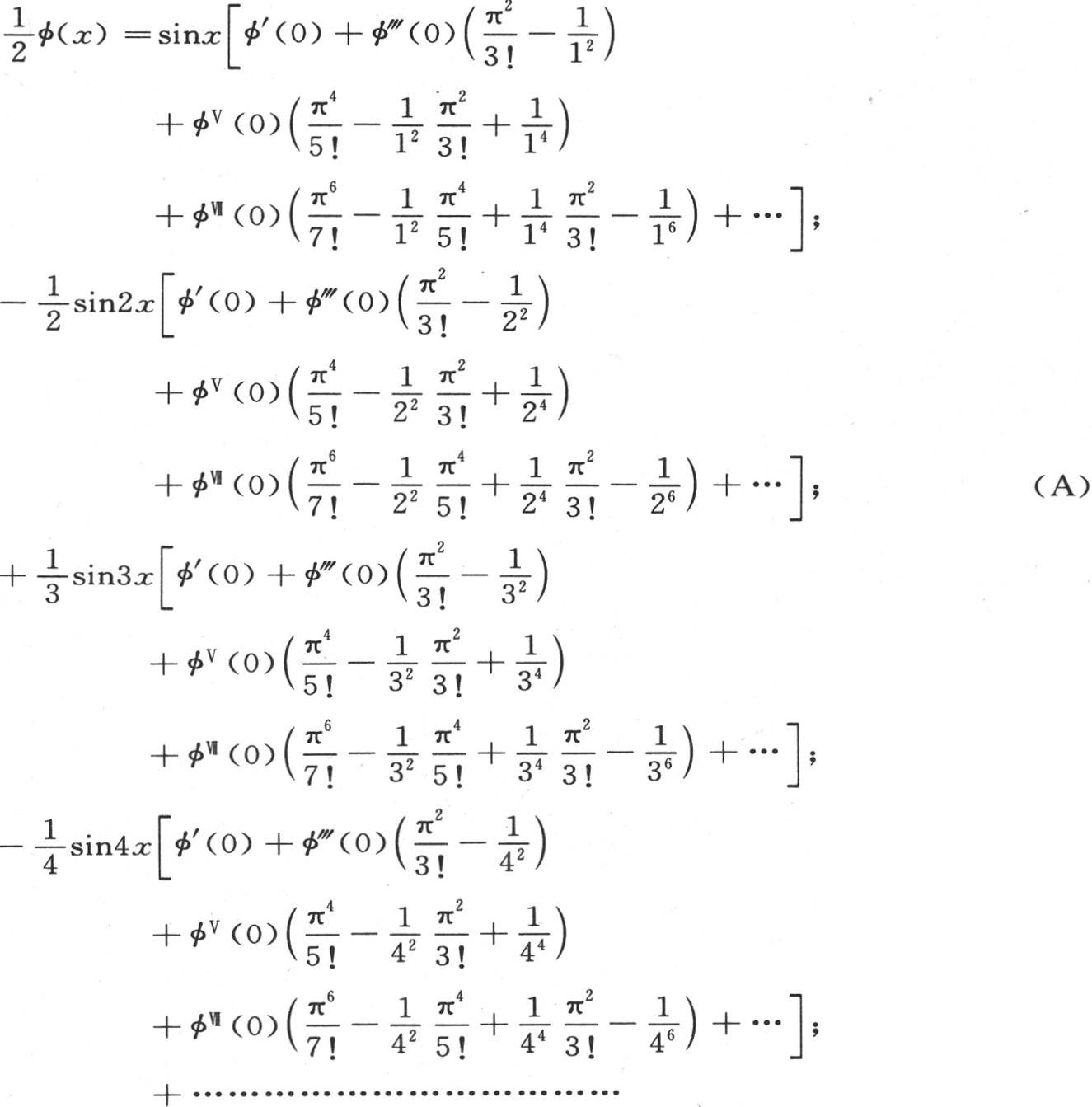
利用上述级数,我们可以把其展开式只含变量奇次幂的任一个所提出的函数,化成多重弧的正弦级数。
216 出现的第一种情况是φ(x)=x的情况;于是我们得到φ′(0)=1, ,φV (0)=0,…,余者亦同。因此,我们得到曾由欧拉所给出的级数
,φV (0)=0,…,余者亦同。因此,我们得到曾由欧拉所给出的级数
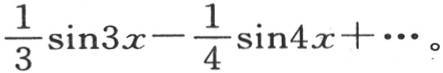
如果我们假定所提出的函数是x3 ,那么我们有φ′(0)=0,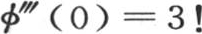 ,φV (0)=0,φVII (0)=0,…,它们给出方程
,φV (0)=0,φVII (0)=0,…,它们给出方程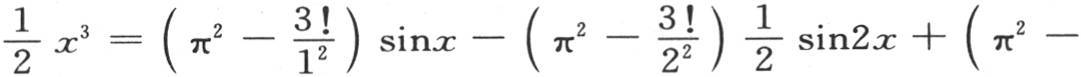
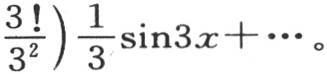
从上面那个方程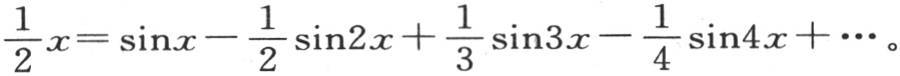 开始,我们可以得到同样的结果。
开始,我们可以得到同样的结果。
事实上,用dx乘两边并积分,我们有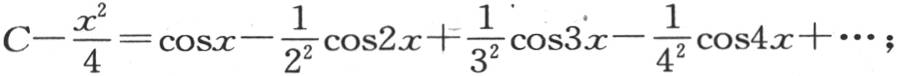 常数C的值是
常数C的值是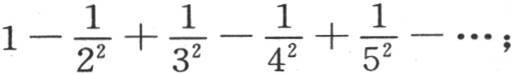 其和已知为
其和已知为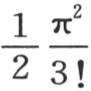 的一个级数。用dx乘方程
的一个级数。用dx乘方程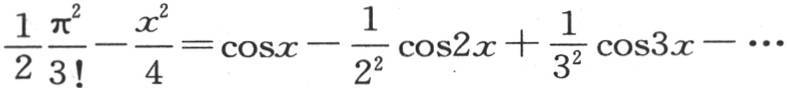 的两边并积分,我们有
的两边并积分,我们有
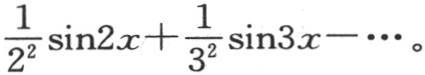
如果现在我们不用x而用它从方程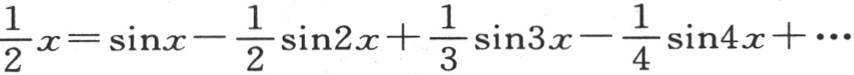 中所导出的值,那么我们将得到和上面一样的同一个方程,即
中所导出的值,那么我们将得到和上面一样的同一个方程,即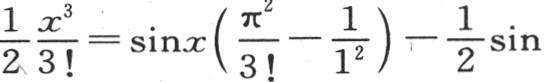
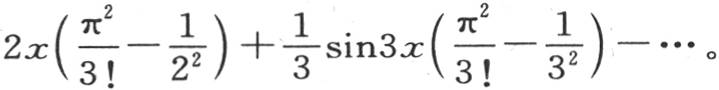
用同样的方法,我们可以得到幂x5 ,x7 ,x9 ,…的多重弧的级数展开式,一般地,可以得到其展开式只含变量奇次幂的每一个函数的多重弧的级数展开式。
217 我们可以把方程(A)(第215目)置于一个现在可以指明的更简单的形式中。首先我们注意到,sinx的系数的一部分是级数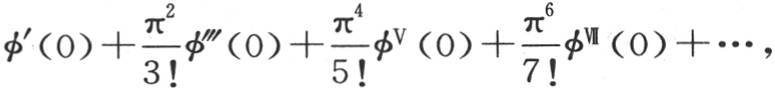 它表示量
它表示量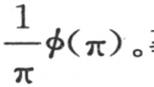 事实上,我们一般有
事实上,我们一般有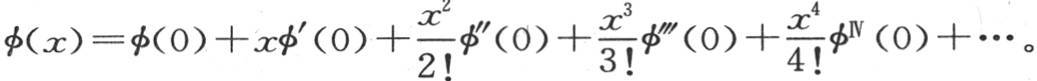
现在由假定,当函数φ(x)只含奇次幂时,我们一定有φ(0)=0,φ″(0)=0,φIV (0)=0,…。因此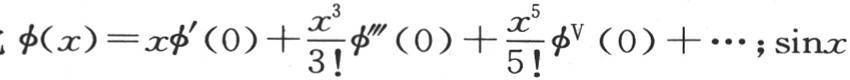 的系数的第二部分通过用
的系数的第二部分通过用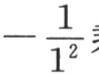 乘级数
乘级数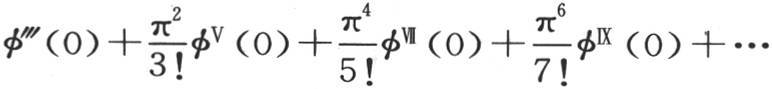 而得到,这个级数的值是
而得到,这个级数的值是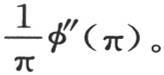 用这种方法,我们可以确定sinx的系数的不同部分,以及sin2x,sin3x,sin4x,…的系数的不同部分。为此,我们可以运用方程:
用这种方法,我们可以确定sinx的系数的不同部分,以及sin2x,sin3x,sin4x,…的系数的不同部分。为此,我们可以运用方程:
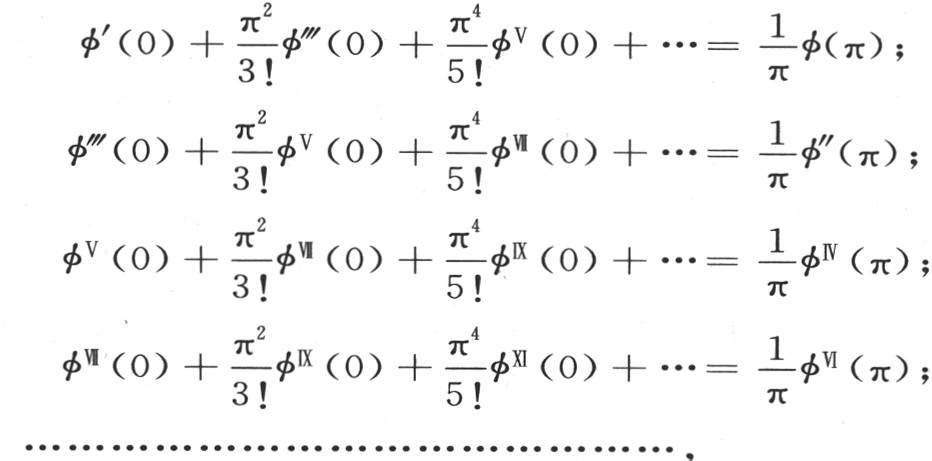
通过这些化简,方程(A)得到下述形式:
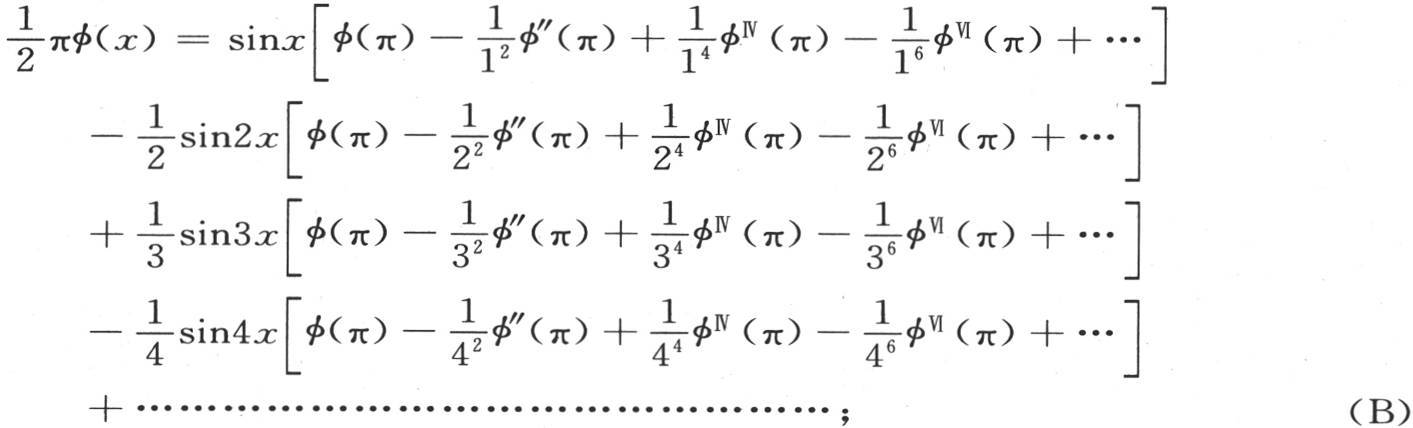
或
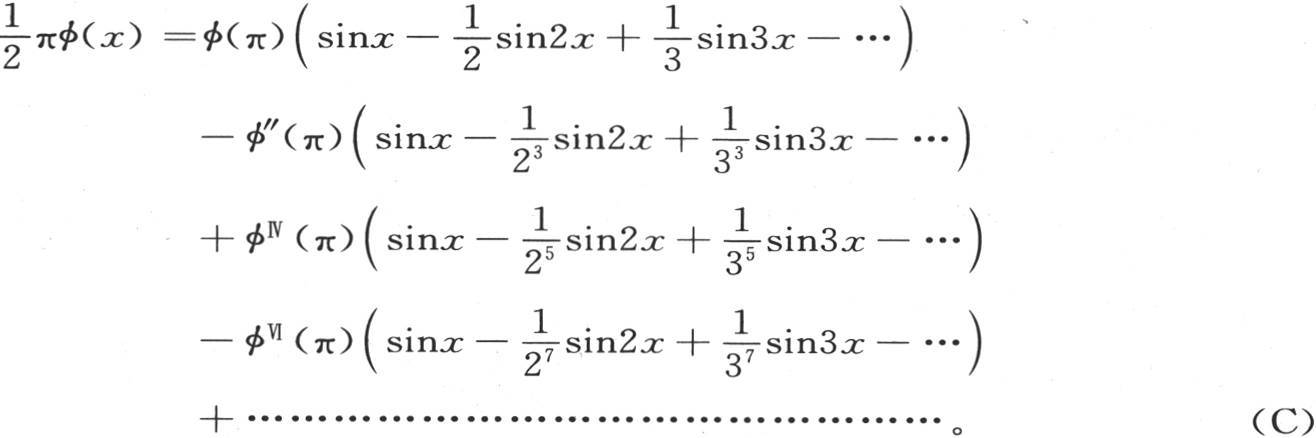
218 每当我们不得不以多重弧的正弦级数来展开所提出的函数时,我们都可以运用这两个公式的一个或者是另一个。例如,如果所提出的函数是ex -e-x ,它的展开式只含x的奇次幂,那么我们将有
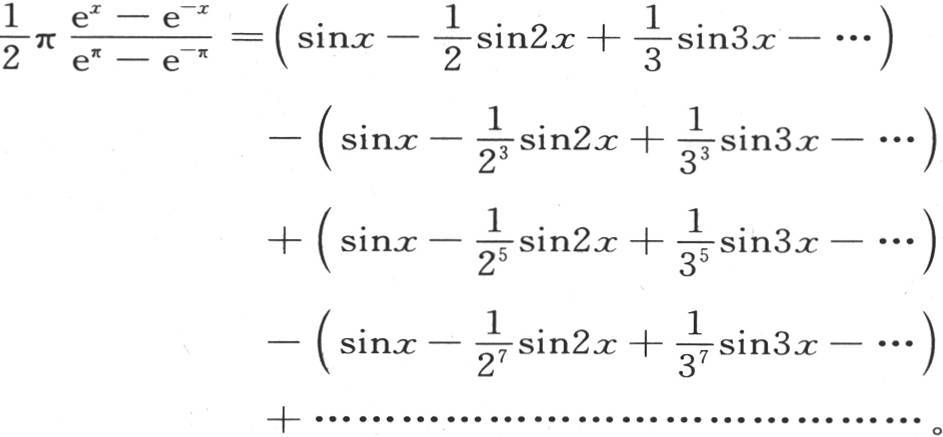
整理sinx,sin2x,sin3x,sin4x,…的系数,并且不用 而代之以它的值
而代之以它的值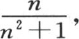 则我们有
则我们有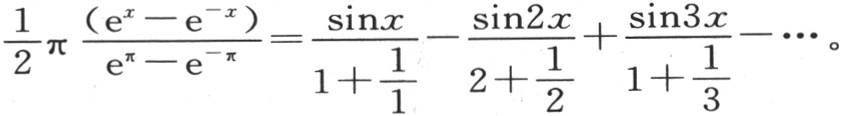
我们应当扩展这些应用,并且从中导出几个值得注意的级数。我们选取上面这个例子是因为看来它在几个问题中都与热传导有关。
219 到目前为止,我们一直假定,需要以多重弧的正弦级数展开的函数,可以根据变量x的幂所安排的级数来展开,并且假定只有奇次幂进入那个级数。我们可以把这同一结果扩展到任何函数上,甚至扩展到那些不连续的和完全任意的函数上。为了使这个命题清楚地成立,我们应当采用提供上述方程(B)的分析,并考查乘sinx,sin2x,sin3x,…的系数的性质是什么。用s表示当n是奇数时乘这个方程中的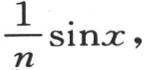 当n是偶数时乘
当n是偶数时乘 的那个量,则我们有
的那个量,则我们有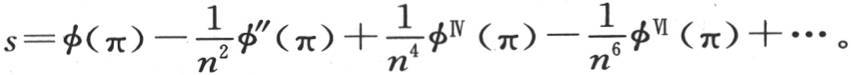
把s看做是π的函数,取两次微分,并比较这些结果,我们得到 这是s的上述值应当满足的一个方程。
这是s的上述值应当满足的一个方程。
现在,在方程 的积分中,把s看做是x的函数,这个积分就是s=acosnx+bsinnx+nsinnx∫cosnxφ(x)dx-ncosnx∫sinnxφ(x)dx。如果n是一个整数,并且x的值等于π,则我们有s=±n∫φ(x)sinnx dx。当n是奇数时,我们应当取正号,当n是偶数时,则应当取负号。在对上述微分方程求解之后,我们应当使x等于半圆周π;运用分部积分,同时注意函数φ(x)只含变量x的奇数幂,并且从x=0到x=π取积分,则可以用项∫φ(x)sinnxdx的展开式来检验我们的结果。
的积分中,把s看做是x的函数,这个积分就是s=acosnx+bsinnx+nsinnx∫cosnxφ(x)dx-ncosnx∫sinnxφ(x)dx。如果n是一个整数,并且x的值等于π,则我们有s=±n∫φ(x)sinnx dx。当n是奇数时,我们应当取正号,当n是偶数时,则应当取负号。在对上述微分方程求解之后,我们应当使x等于半圆周π;运用分部积分,同时注意函数φ(x)只含变量x的奇数幂,并且从x=0到x=π取积分,则可以用项∫φ(x)sinnxdx的展开式来检验我们的结果。
我们立即得到,这一项等于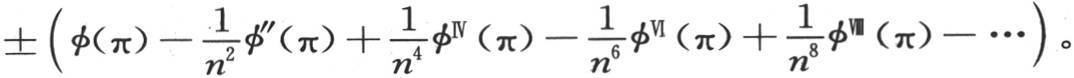
如果我们在方程(B)中代入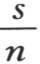 的这个值,同时当这个方程的这一项是奇序号时取符号+,当n是偶序号时取符号-,那么一般地,对于sinnx的系数,我们有∫φ(x)sinnx dx;如此,我们得到由下述方程
的这个值,同时当这个方程的这一项是奇序号时取符号+,当n是偶序号时取符号-,那么一般地,对于sinnx的系数,我们有∫φ(x)sinnx dx;如此,我们得到由下述方程
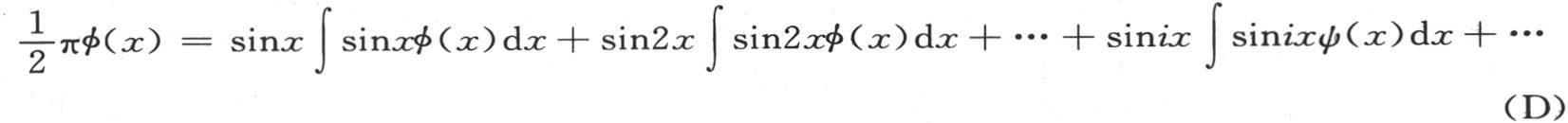
所表示的一个非常值得注意的结果,如果我们从x=0到x=π取积分,那么右边将总是给出函数φ(x)所需要的展开式 【11】 。
220 我们由此看到,进入方程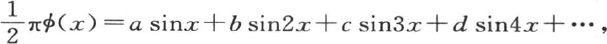 以及我们以前由逐次消元所得到的系数a,b,c,d,e,f,…,是由一般项∫sinixφ(x)dx所表示的值,i是其系数所需要的项数。这个注记是重要的,因为它表明即使是完全任意的函数,怎样也能够以多重弧的正弦级数展开。事实上,如果函数φ(x)由横坐标从x=0延拓至x=π的任一曲线的可变纵坐标来表示,如果我们在这个轴的同一部分作一个纵坐标为y=sinx的已知三角曲线,那么我们不难表示任一积分项的值。我们应当假定,对于对应φ(x)的一个值和sinx的一个值的每一个横坐标x,我们都用第一个值乘第二个值,并且在同一点作一个等于积φ(x)sinx的纵坐标。通过这种连续运算,我们形成第三条曲线,它的纵坐标是与表示φ(x)的任意曲线的纵坐标成比例地压缩了的这条三角曲线的纵坐标。如此,从x=0取到x=π的这条压缩曲线的面积给出sinx的系数的精确值;并且无论对应于φ(x)的这条已知曲线是怎样的,不管是我们能对它给定一个解析方程,还是它不服从于任何规律,显然,它都总是起到以任一方式压缩这条三角曲线的作用;因此,在一切可能的情况中,这条压缩曲线的面积有一个确定的值,它是函数展开式中sinx的系数的值。后面的系数b或者是∫φ(x)sin2xdx的情况亦如此。
以及我们以前由逐次消元所得到的系数a,b,c,d,e,f,…,是由一般项∫sinixφ(x)dx所表示的值,i是其系数所需要的项数。这个注记是重要的,因为它表明即使是完全任意的函数,怎样也能够以多重弧的正弦级数展开。事实上,如果函数φ(x)由横坐标从x=0延拓至x=π的任一曲线的可变纵坐标来表示,如果我们在这个轴的同一部分作一个纵坐标为y=sinx的已知三角曲线,那么我们不难表示任一积分项的值。我们应当假定,对于对应φ(x)的一个值和sinx的一个值的每一个横坐标x,我们都用第一个值乘第二个值,并且在同一点作一个等于积φ(x)sinx的纵坐标。通过这种连续运算,我们形成第三条曲线,它的纵坐标是与表示φ(x)的任意曲线的纵坐标成比例地压缩了的这条三角曲线的纵坐标。如此,从x=0取到x=π的这条压缩曲线的面积给出sinx的系数的精确值;并且无论对应于φ(x)的这条已知曲线是怎样的,不管是我们能对它给定一个解析方程,还是它不服从于任何规律,显然,它都总是起到以任一方式压缩这条三角曲线的作用;因此,在一切可能的情况中,这条压缩曲线的面积有一个确定的值,它是函数展开式中sinx的系数的值。后面的系数b或者是∫φ(x)sin2xdx的情况亦如此。
一般地,为了作系数a,b,c,d,…的值的图,我们应当设想,对于x轴从x=0到x=π的这同一区间,我们已经作了方程为y=sinx,y=sin2x,y=sin3x,y=sin4x,…的曲线;这样,通过用方程为y=φ(x)的一条曲线的对应纵坐标乘所有上述曲线的纵坐标,我们就改变了这些曲线。这些压缩曲线的方程是y=sinxφ(x),y=sin2xφ(x),y=sin3xφ(x),…。
从x=0取到x=π的上面这些曲线的面积,是方程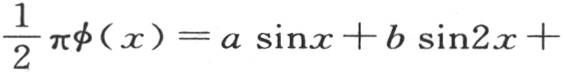
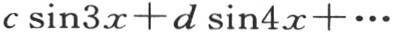 中系数a,b,c,d,…的值。
中系数a,b,c,d,…的值。
221 通过直接确定方程φ(x)=a1 sinx+a2 sin2x+a3 sin3x+…aj sinjx+…中的量a1 ,a2 ,a3 …aj ,…,我们可以检验前面的方程(D)(第219目);为此,我们用sinixdx乘上一个方程的两边,i是一个整数,同时取x=0到x=π的积分,这样,我们有∫φ(x)sinix dx=a1 ∫sinx sinix dx+a2 ∫sin2x sin ix dx+…+aj ∫sinjx sinix dx+…。
现在容易证明,第一,除了项ai ∫sinix sin ix dx之外,进入右边的所有的积分都取值为0;第二,∫sinix sin ix dx的值是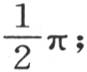 因此我们得到ai 的值,即
因此我们得到ai 的值,即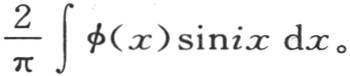
整个问题被简化成考虑进入右边的那些积分的值,简化成证明前面那两个命题。从x=0取到x=π的积分2∫sinjx sin ix dx等于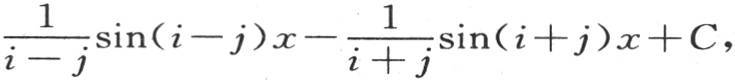 其中i和j是整数。
其中i和j是整数。
由于这个积分必须从x=0开始,所以常数C为零,并且,由于数i和j是整数,所以当x=π时,这个积分的值就变成零;因此,像a1 ∫sinx sin ix dx,a2 ∫sin2x sin ix dx,a3 ∫sin3x sin ix dx,…这样的每一项都变成零,并且,每当数i和j不同时,就出现这个结果。数i和j相等时的情况则不同,因为简化成的积分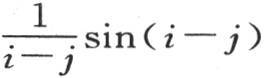 变成
变成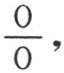 其值为π。因此我们有2∫sinix sinix dx=π;所以我们以一种非常简单的方式得到a1 ,a2 ,a3 ,…,ai ,…的值,即,
其值为π。因此我们有2∫sinix sinix dx=π;所以我们以一种非常简单的方式得到a1 ,a2 ,a3 ,…,ai ,…的值,即,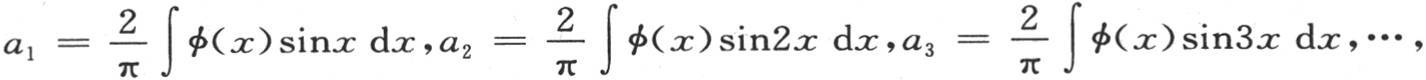
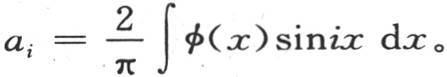
代入这些值,我们有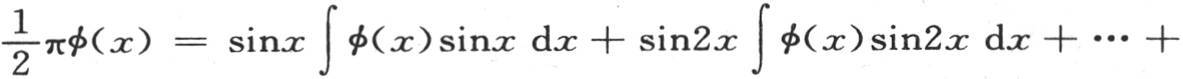
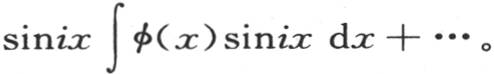
222 最简单的情况是已知函数对包含在0到π之间的变量x的所有值有一个常数值的情况;在这种情况下,若数i是奇数,则积分∫sinix dx等于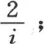 若数i是偶数,则它等于0。因此我们推出在前面曾经得到过的方程
若数i是偶数,则它等于0。因此我们推出在前面曾经得到过的方程
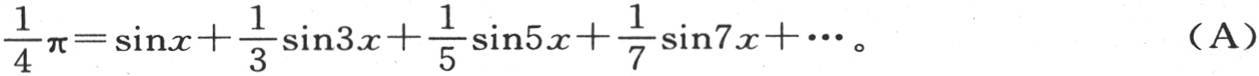
应当注意,当函数φ(x)已经以多重弧的正弦级数展开时,只要变量x在0到π之间,那么级数asinx+bsin2x+csin3x+dsin4x+…的值就和函数φ(x)的值相同;但是当x的值超过数π时,这个性质就一般不成立。
假定需要展开的这个函数是x,由前述定理,我们有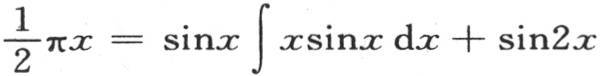
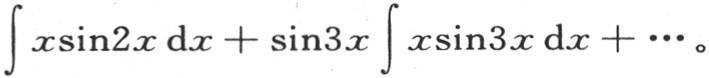
积分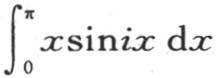 等于
等于 与积分号∫有关的指标0和π表明积分的上下限;当i是奇数时,应当取符号+,当i是偶数时,取符号-。这样,我们有下述方程
与积分号∫有关的指标0和π表明积分的上下限;当i是奇数时,应当取符号+,当i是偶数时,取符号-。这样,我们有下述方程
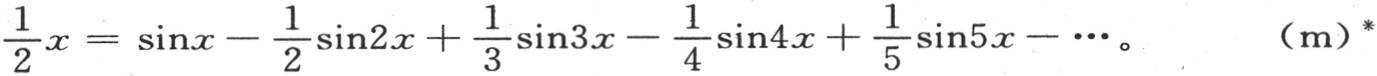
* 这个方程的编号“(m)”是根据法文《文集》本(见勘误表)加上的。——汉译者
223 我们也可以以多重弧的正弦级数展开与只有奇数幂进入其中的那些函数所不同的函数。为了以一个毫无问题的例子说明这种展开式的可能性,我们选择cosx,这个函数只含x的偶次幂,并且可以以下述形式展开:asinx+bsin2x+csin3x+dsin4x+esin5x+…,尽管在这个级数中只有变量的奇次幂进入。
事实上,由前述定理,我们有
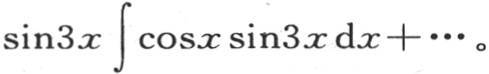
当i为奇数时,积分∫cosx sinix dx等于零,当i为偶数时,这个积分等于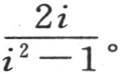 依次假定i=2,4,6,8,…,我们有始终都收敛的级数
依次假定i=2,4,6,8,…,我们有始终都收敛的级数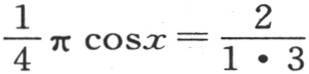
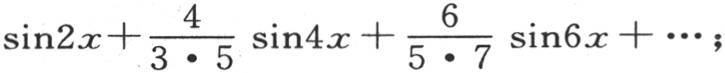 或者是
或者是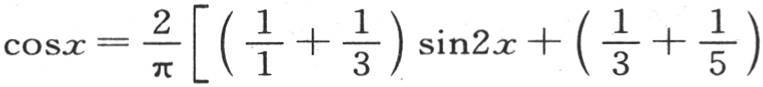
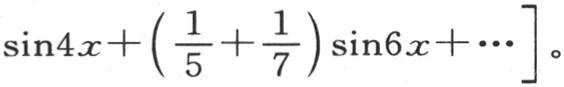
这个结果在它以每一个都只含奇次幂的函数级数展示余弦展开式这一方面,是值得注意的。如果在上述方程中使x等于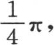
那么我们得到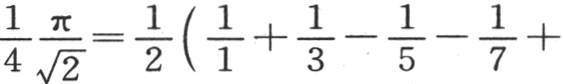
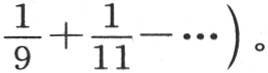
这个级数是已知的〔《无穷小分析导论》(Introd. ad analysin. infinit.),第10章〕。
224 我们对以多重弧的余弦级数展开的无论怎样的一个函数都可以运用类似的分析。
设φ(x)是其展开式待求的函数,我们可以写
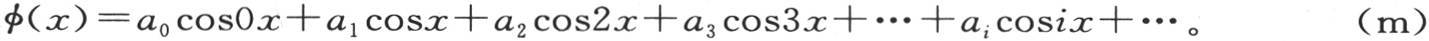
如果用cosjx乘这个方程的两边,并且对右边每一项取从x=0到x=π的积分;那么容易看到,除已经包含cosjx的那一项外,这个积分的值为零。这个观察立即给出系数aj ;一般地,假定j和i是整数,我们只需考虑从x=0取到x=π的积分∫cosjx cosix dx的值就够了。我们有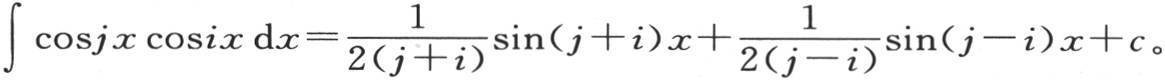
只要j和i是两个不同的数,那么,从x=0取到x=π的这个积分就显然变为零。当这两个数相等时情况则不同。当弧x等于π时,最后一项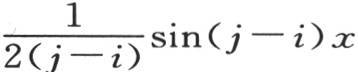 变成
变成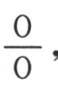 其值为
其值为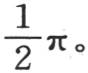 这样,如果我们用cosix乘前述方程(m)的两边,并对它从0到π取积分,那么我们有
这样,如果我们用cosix乘前述方程(m)的两边,并对它从0到π取积分,那么我们有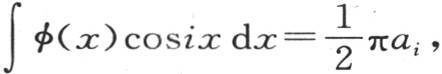 表示系数ai 的值的一个方程。
表示系数ai 的值的一个方程。
为了得到第一个系数a0 ,我们可以注意,在积分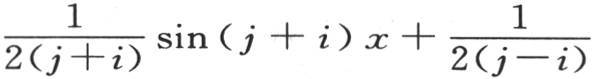
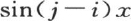 中,如果j=0并且i=0,那么每一项都变成
中,如果j=0并且i=0,那么每一项都变成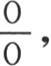 每一项的值都是
每一项的值都是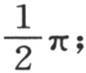 因此,当两个整数j和i不同时,从x=0取到x=π的积分∫cosjx cosix dx为零;当这两个数相等但不等于0时,它等于
因此,当两个整数j和i不同时,从x=0取到x=π的积分∫cosjx cosix dx为零;当这两个数相等但不等于0时,它等于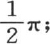 当j和i的每一个都等于0时,它等于π;因此我们得到下述方程,
当j和i的每一个都等于0时,它等于π;因此我们得到下述方程,
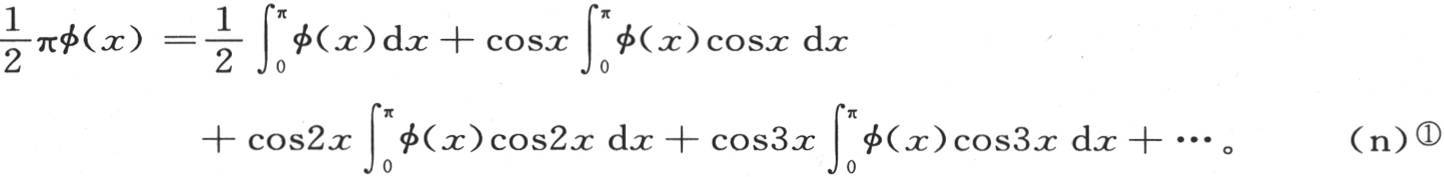
① 与第222目中的(A)相似的步骤在此处不成立;我们还看到,在第177目中有一个类似的结果。——R. L. E.
这个定理和前述定理适合于一切可能的函数,无论它们的性质可以由已知的分析方法来表示,还是它们对应于任意作出的曲线。
225 如果所提出的、需要以多重弧的余弦展开的这个函数就是变量x本身;那么我们可以记方程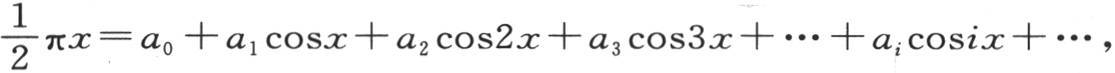 为了确定任意一个系数ai ,我们有方程
为了确定任意一个系数ai ,我们有方程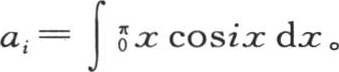 当i是偶数时,这个积分取值为0,当i是奇数时,它等于
当i是偶数时,这个积分取值为0,当i是奇数时,它等于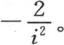 同时我们有
同时我们有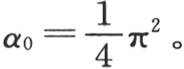 因此,我们形成下述级数,
因此,我们形成下述级数,
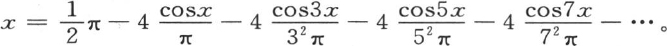
这里我们可以注意到,我们已经得到x的三个不同的展开式,即,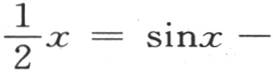
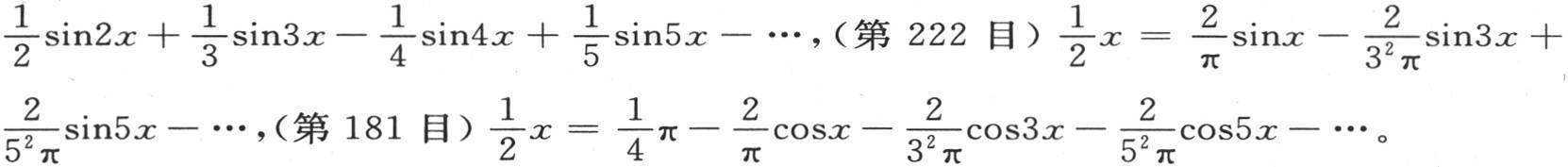
必须注意,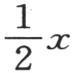 的这三个值不应该看做是相等的;对于x的一切可能的值,上面三个展开式只是当变量x在0到
的这三个值不应该看做是相等的;对于x的一切可能的值,上面三个展开式只是当变量x在0到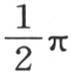 之间时才有共同的值。这三个级数的作图,以及其纵坐标由它们来表示的这些曲线的比较,表明这些函数的值明显的交错重合和发散。
之间时才有共同的值。这三个级数的作图,以及其纵坐标由它们来表示的这些曲线的比较,表明这些函数的值明显的交错重合和发散。
为了给出函数以多重弧的余弦级数展开的第二个例子,我们选择只含变量奇次幂的函数sinx,我们可以假定它以下述形式展开:a+bcosx+ccos2x+dcos3x+…。把一般方程应用到这个特殊情况中,作为所需要的方程,我们得到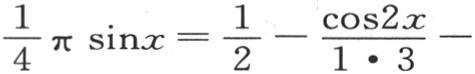
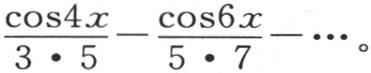 因此,我们得到只含奇次幂的函数以只有变量的偶次幂进入的余弦级数展开的展开式。如果我们对x给定特殊值
因此,我们得到只含奇次幂的函数以只有变量的偶次幂进入的余弦级数展开的展开式。如果我们对x给定特殊值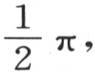 那么我们得到
那么我们得到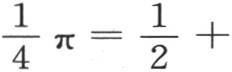
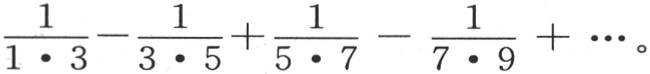 现在,从已知方程,
现在,从已知方程,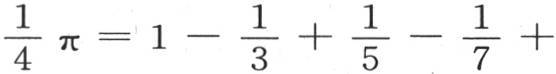
 我们得到
我们得到 和
和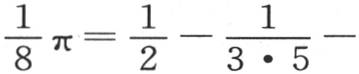

把这两个结果相加,和上面一样,我们有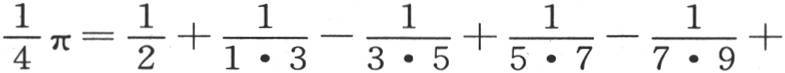
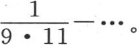
226 由于前面的分析给出了以多重弧的正弦或者是余弦级数展开任一函数的方法,所以,我们不难把它应用到当变量被包含在某个界限内并且有实数值时,或者当变量被包含在其他界限内时,被展开的这个函数有确定的值这样的情况中去。由于这个特殊的情况是在依赖于偏微分方程的物理问题中被提出的,并且以前它是作为不能以多重弧的正弦或者是余弦展开的那些函数的一个例子而被提出的,所以我们停下来考查这种情况。假定我们已经把这种形式的一个函数化为一个级数,当x包含在0到α之间时,该函数的值是常数,当x包含在α到π之间时,该函数的值为0。我们运用一般方程(D),其中,积分应当从x=0取到x=π。由于进入积分符号下的φ(x)的值从x=α到x=π等于0,所以只需从x=0到x=α取积分就够了。如此,用h表示这个函数的常数值,对于这个待求的级数,我们有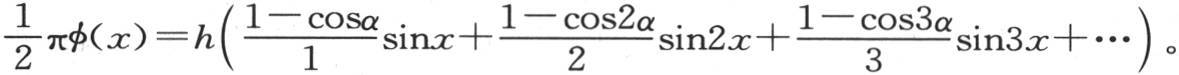
如果我们取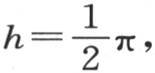 并且用versinx表示弧x的正矢,那么我们有
并且用versinx表示弧x的正矢,那么我们有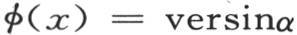
 。 【12】
。 【12】
总是收敛的这个级数是这样一种级数:即如果我们在0到α之间赋予x任一个值,则它的项的和等于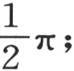 但是如果我们赋予x一个大于α并且小于π的任一个值,则这些项的和等于0。
但是如果我们赋予x一个大于α并且小于π的任一个值,则这些项的和等于0。
在下面这个同样有名的例子中,对于包含在0到α之间的所有x的值,φ(x)的值等于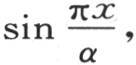 对于α到π之间的x的值,它等于0。为了得到级数所满足的这个条件,我们运用方程(D)。
对于α到π之间的x的值,它等于0。为了得到级数所满足的这个条件,我们运用方程(D)。
这些积分应当从x=0取到x=π;但是,在所讨论的这个情况中,只需从x=0到x=α取这些积分就够了,因为在其余的区间里,φ(x)的值假定为0。因此我们得到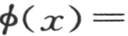
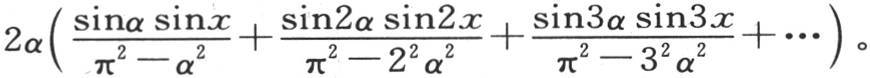
如果我们假定α等于π,那么除第一项外,这个级数的所有的项都为0,第一项变为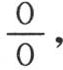 它的值是sinx;这样我们有φ(x)=sinx。
它的值是sinx;这样我们有φ(x)=sinx。
227 我们可以把同样的分析扩大到这样一种情况中去:由φ(x)所表示的纵坐标原来是由不同部分所组成的一条曲线的纵坐标,这些不同部分有些可能是曲线弧,其余的是直线段。例如,设需要以多重弧的余弦级数来展开的函数值,在从x=0到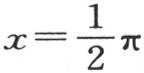 内是
内是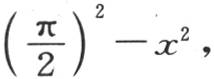 在
在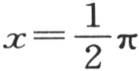 到x=π内是0。我们将运用一般方程(n),并且,在给定的区间内作积分时,我们得到,当i具有2n+1的形式时,一般项 【13】
到x=π内是0。我们将运用一般方程(n),并且,在给定的区间内作积分时,我们得到,当i具有2n+1的形式时,一般项 【13】 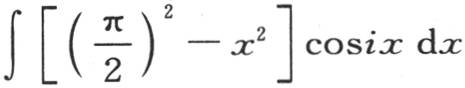 等于
等于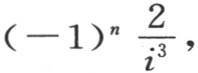 当i是一个奇数的两倍时,它等于
当i是一个奇数的两倍时,它等于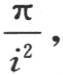 当i是一个奇数的四倍时,它等于
当i是一个奇数的四倍时,它等于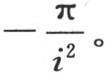 另一方面,对第一项
另一方面,对第一项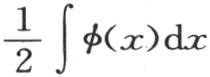 的值,我们得到
的值,我们得到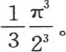 这样,我们有下面的展开式:
这样,我们有下面的展开式:
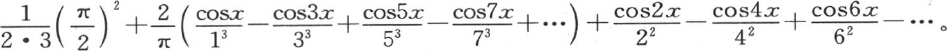
右边由以一些抛物线弧和直线段所组成的一条曲线来表示。
228 同样地,我们可以得到表示梯形周线的纵坐标的一个x的函数的展开式。假定φ(x)在从x=0到x=α内等于x,从x=α到x=π-α,该函数等于α,最后,从x=π-α到x=π,则等于π-α。为了把它化为多重弧的正弦级数,我们运用一般方程(D)。一般项∫φ(x)sinix dx由三个不同的部分组成,对于sinix的系数,在简化后,当i是奇数时,我们有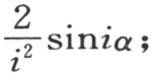 但是当i是偶数时,这个系数就变成0。因此,我们得到方程
但是当i是偶数时,这个系数就变成0。因此,我们得到方程
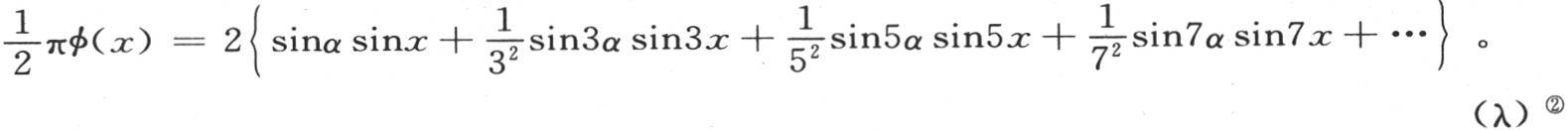
② 傅立叶所给出的这个级数和其他级数的精确性得到汤姆森爵士在第181页的脚注所引的那篇论文的支持。——A. F.
如果我们假定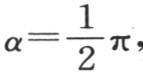 那么,这个梯形就与一个等腰三角形重合,并且,和上面一样,对于这个三角形周线的方程,我们有
那么,这个梯形就与一个等腰三角形重合,并且,和上面一样,对于这个三角形周线的方程,我们有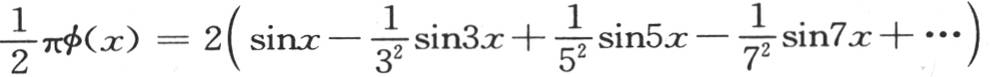 , 【14】 这是一个无论x取什么值,都总是收敛的级数。一般地,我们在展开各种函数时所得到的这些三角级数总是收敛的,不过我们现在还不必在此处证明这一点;因为组成这些级数的项只是给出温度值的级数的项的系数;并且,这些系数受迅速递减的某种指数量的影响,因此,最后的级数是极收敛的。对于那些只有多重弧的正弦和余弦进入其中的级数,尽管它们表示不连续线段的纵坐标,但是我们同样容易证明它们是收敛的。这并不完全由这些项的值连续递减这一事实所决定;因为,这个条件不足以建立一个级数的收敛性。在项数不断增加时,我们所得到的这些值应当愈来愈趋于一个固定的极限,并且应当与它只相差一个比任一给定量都小的量,这才是必需的:这个极限就是这个级数的值。现在,我们可以严格证明所讨论的级数满足最后这个条件。
, 【14】 这是一个无论x取什么值,都总是收敛的级数。一般地,我们在展开各种函数时所得到的这些三角级数总是收敛的,不过我们现在还不必在此处证明这一点;因为组成这些级数的项只是给出温度值的级数的项的系数;并且,这些系数受迅速递减的某种指数量的影响,因此,最后的级数是极收敛的。对于那些只有多重弧的正弦和余弦进入其中的级数,尽管它们表示不连续线段的纵坐标,但是我们同样容易证明它们是收敛的。这并不完全由这些项的值连续递减这一事实所决定;因为,这个条件不足以建立一个级数的收敛性。在项数不断增加时,我们所得到的这些值应当愈来愈趋于一个固定的极限,并且应当与它只相差一个比任一给定量都小的量,这才是必需的:这个极限就是这个级数的值。现在,我们可以严格证明所讨论的级数满足最后这个条件。
229 取前面的方程(λ),其中,我们可以赋予x任一个值;我们把这个量看做是一个新的纵坐标,它产生下面的结构。
在x和y平面上(见图8)作一个其底Oπ等于半圆周长,其高为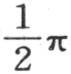 的矩形;在与底平行的边的中点m上,让我们垂直于矩形平面作一条等于
的矩形;在与底平行的边的中点m上,让我们垂直于矩形平面作一条等于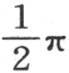 的直线段,并从这条直线段的顶点向矩形的四个角作直线。这样就形成一个四棱锥。如果我们现在从在这个矩形短边上的点O来测定等于α的任一线段,并且通过这条线段的端点作一个平行于底Oπ并且垂直于矩形平面的平面,那么这个平面和这个固体所共有的截面是一个其高等于α的梯形。正如我们刚才已经看到的,这个梯形的周线的可变纵坐标等于
的直线段,并从这条直线段的顶点向矩形的四个角作直线。这样就形成一个四棱锥。如果我们现在从在这个矩形短边上的点O来测定等于α的任一线段,并且通过这条线段的端点作一个平行于底Oπ并且垂直于矩形平面的平面,那么这个平面和这个固体所共有的截面是一个其高等于α的梯形。正如我们刚才已经看到的,这个梯形的周线的可变纵坐标等于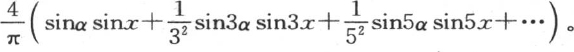
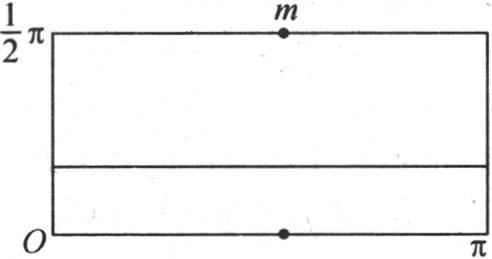
图8
由此得到,若把我们所形成的这个四棱锥表面上的一点的坐标称为x,y,z,对于在x=0,x=π,y=0,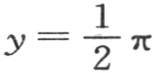 的界限之间的这个多面体的表面的方程,我们有
的界限之间的这个多面体的表面的方程,我们有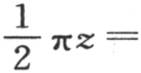
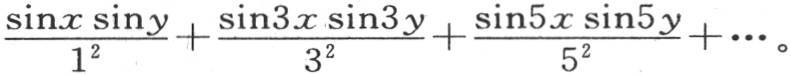
这个收敛级数总是给出纵坐标z的值,或者从x和y平面到这个面任一点的距离的值。
因此,由多重弧的正弦或者是余弦所形成的这个级数适合于在确定的界限之间表示所有可能的函数,以及其形状不连续的线和面的纵坐标。不仅这些展开式的可能性已经得到证明,而且计算这个级数的项也不难;在方程φ(x)=a1 sinx+a2 sin2x+a3 sin3x+…ai sinix+…中,任一个系数的值都是一个定积分的值,即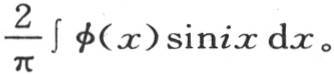
无论函数φ(x)或者是它所表示的这条曲线的形状如何,这个积分都有一个可以引进这个方程的确定的值。这些定积分的值与在一个给定区间内包含在这条曲线和轴之间的这整个面积∫φ(x)dx的那些值类似,或者是与诸如这个面积的重心或任一固体的重心的纵坐标那样的力学量类似。显然,无论固体的图形是规则的,还是我们赋予它们完全任意的形式,所有这些量都有可以指定的值。
230 如果我们把这些原理运用到振弦运动的问题上去,那么我们就能够解决在丹尼尔·伯努利(Daniel Bernoulli)的研究中首次出现的困难。这位几何学家所给出的解假定任一函数都可以以多重弦的正弦或者是余弦级数展开。现在,这个命题的所有证明中最彻底的,就是旨在实际上把一个给定函数分解成带有确定系数的这样一种级数的证明。
在运用偏微分方程的研究中,常常容易得到其和组成一个更一般的积分的解;但是,这些积分的运用需要我们确定它们的范围,并且能够清楚地把它们表示通解的情况和它们只包含部分解的情况区分开来。特别是必须指定常数,并且,运用的困难在于发现这些系数。值得注意的是,我们能够用收敛级数,并且,正如我们在后面将要看到的,用定积分,来表示不服从于连续规律的线和面的纵坐标 【15】 。我们由此看到,如果有两个函数,无论它们的变量在包含在两个给定的界限内取任何一个值,这两个函数都有相同的值,即使在这样的两个函数中当用包含在另一个区间中的一个数来代替这个变量时这两个代替的结果是不相同的,那么,我们也仍然应当允许这样的函数进入分析。具有这个性质的函数由不同的线段来表示,这些线段只在它们轨迹的一个确定部分重合,并且提供有限密切(finite osculation)的一个奇异类型。这些考虑产生于偏微分方程的演算;它们对这个演算给予了新的说明,并且有助于它在物理理论中的应用。
231 以多重弧的余弦或者是正弦表示任一函数展开式的这两个一般方程,引出解释这些定理的真实意义和指出其应用的几个注记。
如果在级数a+bcosx+ccos2x+dcos3x+ecos4x+…中,我们取x的值为负,那么这个级数保持不变;如果我们用圆周长2π的任一倍数来扩大这个变量,它仍然保持它的值。因此,在方程
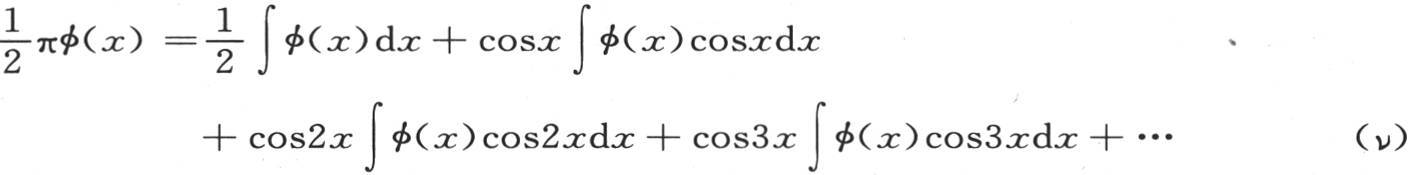
中,函数φ是周期函数,并且由一条由许多相等的弧所组成的曲线来表示,每一个这样的弧段都对应这个横轴上等于2π的一个区间。此外,每一个弧段都由两个对称的分支所组成,这个两分支对应着等于2π区间的两个等分。
这样,假定作任一形状的线段φφa(见图9),这条线段对应着一个等于π的区间。
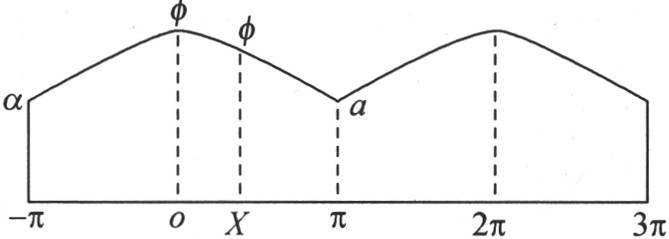
图9
如果我们要求一个级数具有α+bcosx+ccos2x+dcos3x+…的形式,使得当用包含在0到π之间的任一个值X来代替x时,我们求得这个级数的值为纵坐标Xφ的值,那么,这个问题不难解决:因为由方程(ν)所给出的系数是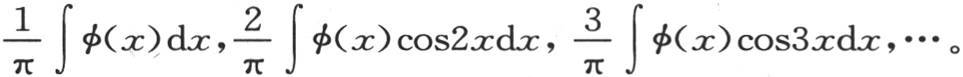
由于从x=0取到x=π的这些积分总有像面积Oφaπ那样的可测值,并且由这些系数所形成的这个级数总是收敛的,所以,线段φφa的纵坐标不可能不由展开式α+bcosx+ccos2x+dcos3x+ecos4x+…来严格表示。
弧φφa是完全任意的;但是,这条曲线其他部分的情况则不同,相反,它们是确定的;因此,与0到-π区间对应的弧φα的弧φa相同;整个弧αφa在这个轴长为2π的相邻部分重复。
我们可以在方程(ν)中改变积分区间。如果我们从x=-π到x=π取积分,则结果将翻一倍:如果积分区间是0到2π,而不是0到π,结果仍然翻一倍。一般地,我们用符号 表示变量等于a时开始、变量等于b时结束的积分;我们把方程(n)写成下面的形式:
表示变量等于a时开始、变量等于b时结束的积分;我们把方程(n)写成下面的形式:
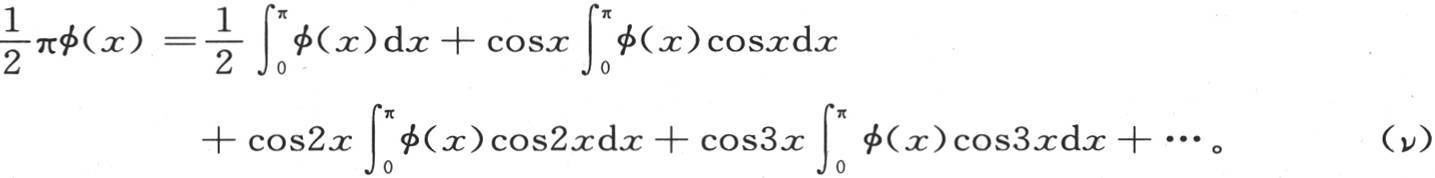
不从x=0到x=π取积分,我们可以从x=0到x=2π,或者是从x=-π到x=π来取这些积分;但是,在这两种情况的每一个当中,我们都应当在方程左边用πφ(x)代替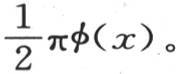
232 在以多重弧的正弦给出任一函数的展开式的方程中,当变量x变成负数时,级数要变号,并且保持相同的绝对值;当变量以圆周长2π的任一倍数增加和减少时,它保持它的值和它的符号不变。对应于区间0到π的弧φφa(见图10)是任意的;这条曲线的所有其他部分是确定的。与区间0到-π对应的弧φφα和已知弧φφa的形式相同;只不过它的位置相反。整个弧αφφφφa在从π到3π的区间内,并且在所有类似的区间内重复。我们写这个方程如下:
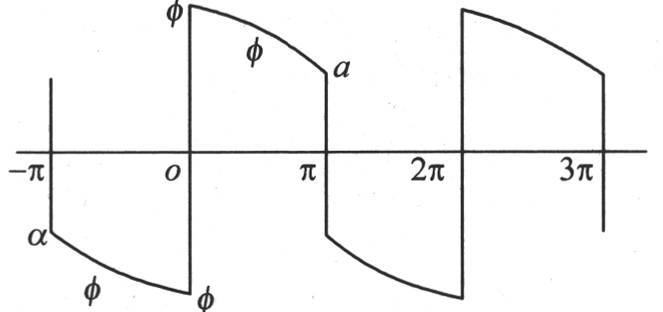
图10
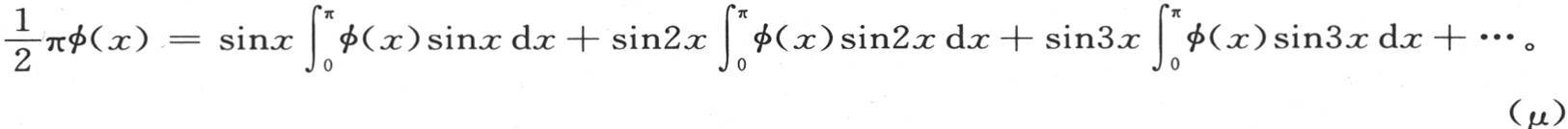
我们可以改变这些积分的积分区间,用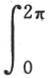 或者是
或者是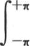 来代替
来代替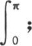 不过在这两种情况中,都应当在左边用πφ(x)代替
不过在这两种情况中,都应当在左边用πφ(x)代替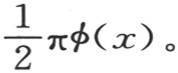
233 以多重弧的余弦展开的函数φ(x),由在从-π到+π的区间内以对称地处在y轴两边的两条相等的弧所形成的一条曲线来表示(见图11);因此这个条件被表示成φ(x)=φ(-x)。
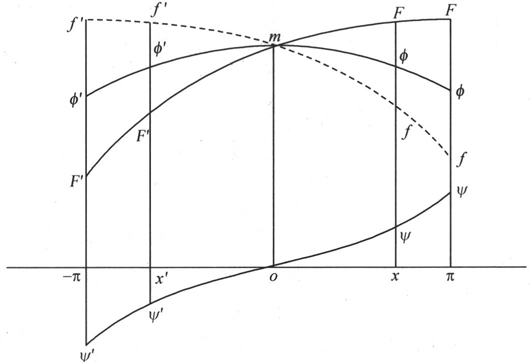
图11
相反,表示函数ψ(x)的这条曲线在同一区间内由两条相反的弧所组成,这两条弧是由方程ψ(x)=-ψ(-x)来表示。
在从-π到+π的区间内,由一条任意画出的曲线所表示的任一函数F(x),总可以划分成像φ(x)和ψ(x)那样的两个函数。事实上,如果曲线F′F′mFF表示函数F(x),并且我们在点o建立一个纵坐标om,那么,过点m,我们总可以向轴om的正向作一条与已知曲线的弧mF′F′相类似的弧mff,向这同一轴的负向作一条与弧mFF相类似的弧mf′f′;这样,我们肯定可以过点m作一条曲线φ′φ′mφφ,这条曲线把每一个纵坐标xF或者是x′f′和相应的纵坐标xf或者是x′F′之间的差分成两个相等的部分。我们也肯定可以作曲线ψ′ψ′oψψ,它的纵坐标计量F′F′mFF的纵坐标和f′f′mff的纵坐标之间的半差(half-difference)。如此,由于曲线F′F′mFF和曲线f′f′mff的纵坐标分别由F(x)和f(x)来表示,所以我们显然有f(x)=F(-x);同样,当用φ(x)表示φ′φ′mφφ的纵坐标,用ψ(x)表示ψ′ψ′oψψ的纵坐标时,我们有F(x)=φ(x)+ψ(x)和f(x)=φ(x)-ψ(x)=F(-x),因此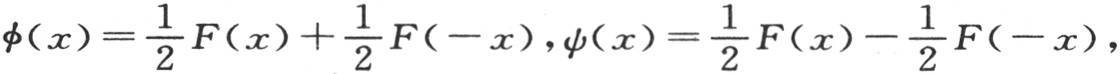 由此我们得到φ(x)=φ(-x),ψ(x)=-ψ(-x),作图以另一种方式使它们成为显然的。
由此我们得到φ(x)=φ(-x),ψ(x)=-ψ(-x),作图以另一种方式使它们成为显然的。
因此,其和等于F(x)的这两个函数φ(x)和ψ(x),一个可以以多重弧的余弦展开,另一个可以以多重弧的正弦展开。
如果我们对第一个函数使用方程(ν),对第二个函数使用方程(μ),在每一种情况中都从x=-π到x=π取积分,并且把这两个结果相加,则我们有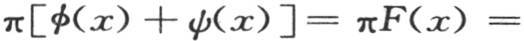
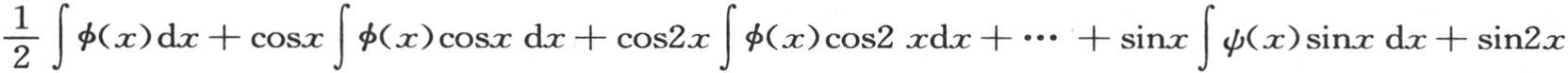 ∫ψ(x)sin2xdx+…这些积分应当从x=-π取到x=π。现在可以注意到,在积分
∫ψ(x)sin2xdx+…这些积分应当从x=-π取到x=π。现在可以注意到,在积分 我们可以用φ(x)+ψ(x)代替φ(x)而不改变它的值:因为,对于x轴的正向和负向,由于函数cosx由两个相似的部分组成,相反,函数ψ(x)由两个相反的部分组成,所以,积分
我们可以用φ(x)+ψ(x)代替φ(x)而不改变它的值:因为,对于x轴的正向和负向,由于函数cosx由两个相似的部分组成,相反,函数ψ(x)由两个相反的部分组成,所以,积分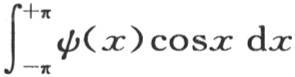 等于0。如果我们用cos2x或者是cos3x,一般地,用cosix代替cosx,i是从0到无穷的任一整数,那么,情况亦如此。因此,积分
等于0。如果我们用cos2x或者是cos3x,一般地,用cosix代替cosx,i是从0到无穷的任一整数,那么,情况亦如此。因此,积分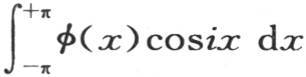 与积分
与积分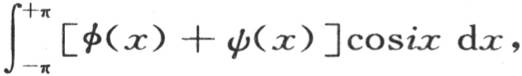 或者是
或者是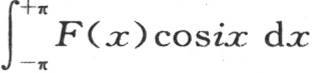 相同。同样显然的是,由于积分
相同。同样显然的是,由于积分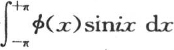 为0,所以,积分
为0,所以,积分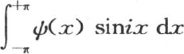 等于积分
等于积分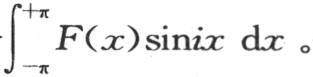 因此,我们得到下面用于以多重弧的正弦和余弦展开任一函数的方程(p):
因此,我们得到下面用于以多重弧的正弦和余弦展开任一函数的方程(p):

234 进入这个方程的函数F(x)由任一形状的一条曲线F′F′FF来表示。与-π到+π的区间对应的弧F′F′FF是任意的;这条曲线的所有其他部分都是确定的,并且弧F′F′FF在每一个其长为2π的相邻区间中重复。我们将经常应用这个定理,经常应用前面的方程(μ)和(ν)。
如果假定在从-π到+π的区间内,方程(p)中的函数F(x)由一条曲线表示,该曲线由处于对称位置的两等弧所组成,那么,所有含正弦的项都变为0,我们得到方程(ν)。相反,如果表示已知函数F(x)的曲线由位置相反的两等弧所组成,那么,所有不含正弦的项都消掉,我们得到方程(μ)。当使函数F(x)服从其他条件时,我们得到其他结果。
在一般方程(p)中,如果我们用量 代替变量x,x表示另一个变量,2r表示包含代表F(x)的弧的区间长度;那么,这个函数就变成
代替变量x,x表示另一个变量,2r表示包含代表F(x)的弧的区间长度;那么,这个函数就变成 我们可以用f(x)来表示这个函数。积分区间x=-π和x=π变成
我们可以用f(x)来表示这个函数。积分区间x=-π和x=π变成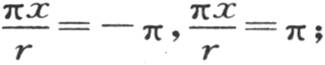 因此,在这个代换之后,我们有
因此,在这个代换之后,我们有
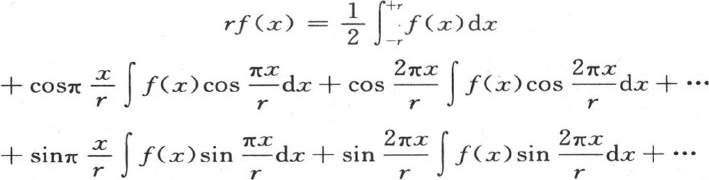
所有这些积分必须像第一个一样从x=-r取到x=+r。如果在方程(ν)和(μ)中作同样的代换,那么我们有
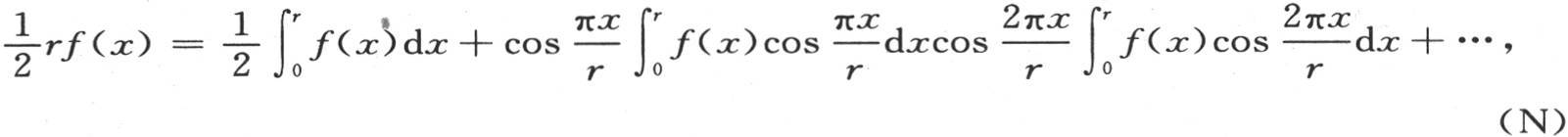
和
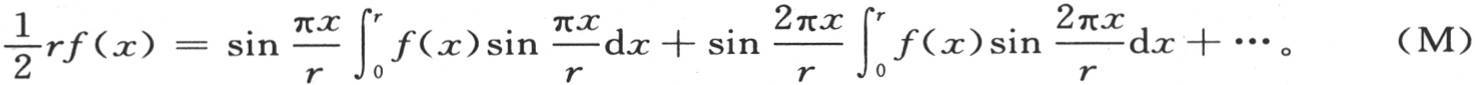
在第一个方程(P)中,这些积分应当从x=0取到x=2r,当用X表示整个区间2r时,我们有 【16】
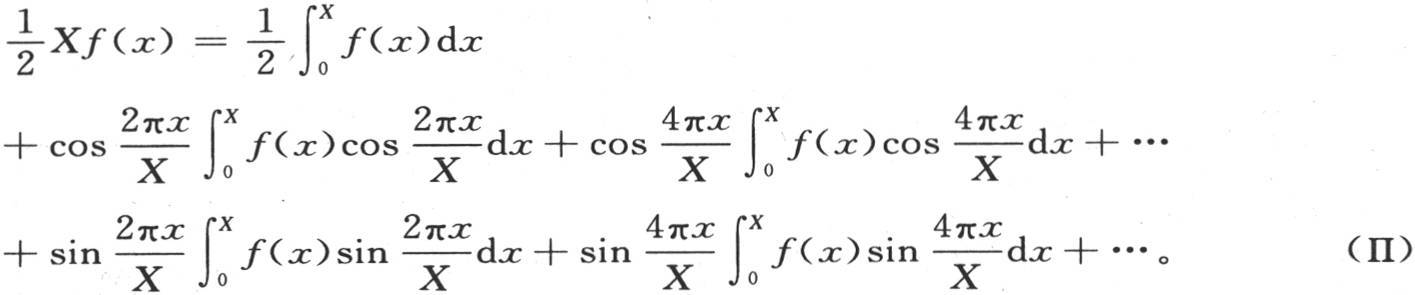
235 就函数的三角级数展开式而言,我们从本节已经证明的那些内容得到,如果我们提出一个函数,在x=0到x=X的确定区间内它的值由任意作出的一条曲线的纵坐标来表示;那么我们总可以只含正弦或者是只含余弦,或者是多重弧的正弦和余弦,或者是只含奇数倍数的余弦,来展开这个函数。为了确定这些级数的项,我们应当运用方程(M),(N),(P)。
表示温度初始状态的函数如果不简化成这种形式,热理论的基本问题就不能完全解决。
根据多重弧的余弦或者是正弦所安排的这些三角级数,和那些其项包含着变量的逐次幂的级数一样,属于初等分析。这些三角级数的系数是确定的面积,幂级数的系数是通过微分所给出的一些函数,并且,在这些函数中,我们对变量指派一个确定的值。关于三角级数的使用和性质,我们本来可以增加一些注记;不过我们只限于简短地阐明与我们所关心的这个理论具有最直接联系的那些注记。
第一、根据多重弧的正弦或者是余弦所安排的级数总是收敛的;也就是说,一旦对变量赋予非虚数的任一个值,那么这些项的和就愈来愈收敛于一个唯一确定的极限,这个极限就是这个被展开的函数的值。
第二、如果我们有对应于一个已知级数a+bcosx+ccos2x+dcos3x+ecos4x+…的函数f(x)的表达式,并且有另一个函数的表达式,它的已知展开式是a+βcosx+γcos2x+δcos3x+εcos4x+…,那么在实际的项中我们容易得到复合级数aα+bβ+cγ+dδ+eε+… 【17】 的和,一般地,容易得到级数aα+bβcosx+cγcos2x+dδcos3x+eεcos4x+…的和,这个级数由逐项比较这两个已知级数而成。这个注记对任一数目的级数都适合。
第三、以多重弧的正弦和余弦级数给出一个函数F(x)的展开式的级数(P)(第234目),可以安排成下述形式:

α是一个新变量,它在积分后消去。
这样我们有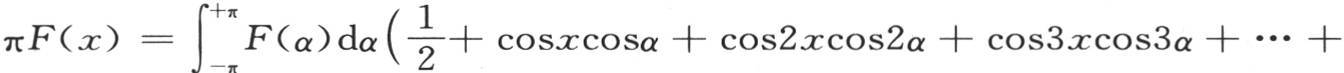
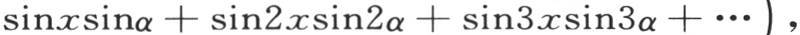 或者是
或者是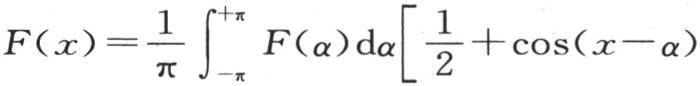
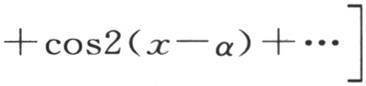
因此,用∑cosi(x-α)表示上一个级数的和,取i=1到i=∞,我们有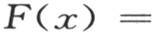
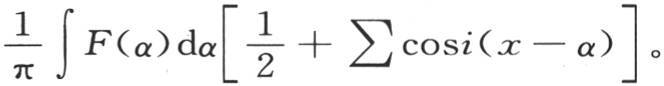
表达式 表示x和α的一个函数,因此,如果用任一函数F(α)乘以它,并且对α在α=-π到α=π之间取积分,那么,所提出的函数F(α)就变成乘以半圆周π的x的同类函数(like function)。在后面,我们会看到具有我们刚才所阐明的性质的诸如
表示x和α的一个函数,因此,如果用任一函数F(α)乘以它,并且对α在α=-π到α=π之间取积分,那么,所提出的函数F(α)就变成乘以半圆周π的x的同类函数(like function)。在后面,我们会看到具有我们刚才所阐明的性质的诸如 的量的特征是什么。
的量的特征是什么。
第四、由于方程(M),(N)和(P)(第234目)一旦除以r,便给出一个函数f(x)的展开式,所以,如果在这些方程中,我们假定区间r变得无穷大,那么级数的每一项就都是无穷小的积分元;这样,这个级数的和就由一个定积分来表示。当物体有确定的体积时,表示初始温度并且进入偏微分方程积分的任意函数,就应当由与方程(M),(N)和(P)的相类似的级数展开;但是,正如在本书处理热的自由扩散的过程中所要解释的(第9章),当物体的体积不确定时,这些函数就呈现为一些定积分的形式。
第6节注。关于其值在某些界限内以多重弧的正弦和余弦级数任意给定的函数的展开式问题,关于在这些界限上与这样的级数的值有关的问题,以及这种级数的收敛性,其值的不连续性等等,主要权威有
泊松,《热的数学理论》(Théorie mathématique de la Chaleur),巴黎,1830年,第7章,第92—102目,“论以一组周期量表示任意函数的方法”(Sur la manière d'exprimer les fonctions arbitraires par des séries de quantités périodiques),或者更简洁地,在他的《力学论著》(Traité de Mécanique)中,第325—328目。泊松关于这一主题的原始论文发表在《综合工艺学校学报》(Journal de l'Ecole Polytechnique)上,第18册,第417—489页,1820年,以及第19册,第404—509页,1823年。
德·摩根,《微积分计算》,伦敦,1842年,第609—617页。展开式的证明似乎是原始的。在展开式的验证中,作者遵循泊松的方法。
斯托克斯,《剑桥哲学会刊》(Cambridge Philosophical Transactions),1847年,第8卷,第533—556页,“周期级数和的临界值”(On the Critical values of the sums of Periodic Series)。第1节,“确定以正弦或余弦级数展开的不连续性的方法和求导出函数展开式的方法”(Mode of ascertaining the nature of the discon tinuity of a function which is expanded in a series of sines or cosines, and of obtaining the developments of the derived functions)。其中有图解论证。
汤姆森和泰特,《自然哲学》,牛津,1867年,第1卷,第75—77目。
唐金(Don Kin),《声学》(Acoustics),牛津,1870年,第72—79目,以及第4章的附录。
马蒂厄,《数学物理教程》,巴黎,1873年,第33—76页。
不含把任意乘数引入级数逐个项的完全不同的讨论方法由下列作者所发明:
狄利克雷,《克雷尔学报》(Crelle's Journal),柏林,1829年,第4卷,第157—169页。“论用于表示有界任意函数的三角级数的收敛”(Sur la convergence des séries trigonométrigues qui serrent à représenter une fonction arbitraire entre les limites données)。这篇论文的方法完全值得仔细研究,然而在英文教材中至今尚未看到。这位作者另一篇更长的论文载于多佛的《物理学索引》(Repertorium der Physik),柏林,1837年,第1卷,第152—174页。“用正弦和余弦级数表示完全任意的函数”(Ueber die Darstellung ganz uillkiikrlicher Functionen durch Sinusund Cosinusreihen)。G. L. 狄利克雷。
其他方面由下列作者给出:
德克森,《克雷尔学报》,1829年,第4卷,第170—178页。“根据一个角的多倍的正弦和余弦收敛fortschreitenden级数”(Ueber die Converygenz einer nach den Sinussen und Cosinussen der Vielfachen eines Winkels fortschreitenden Reihe)。
贝塞尔,《天文学通讯》(Astronomische Nachrichten),阿尔托纳,1839年,第230—238页。“用多倍的正弦和余弦表示一个函数φ(x)”(Ueber den Ausdruck einer Function φ(x) durch Cosinusse und Sinusse der Vielfachen von x)。
最后三位作者的论文由黎曼所评论,《数学全集》,莱比锡,1876年,第221—225页。“关于利用三角级数表示一个函数的可能性”(Ueber die Darstellbarkeit einer Function durch eine Trigonometrische Reihe)。
哈密尔顿爵士发表过一篇论振荡函数和它们的性质的论文,《爱尔兰皇家科学院会刊》(Transactions of the Royal Irish Academy),1843年,第19卷,第264—321页。这一阶段有可能进行介绍性和总结性评论的研究。
德弗勒斯、布尔和其他人关于以二重积分(傅立叶定理)展开任意函数这一主题研究的论著将在第9章第361、362目的注释中提及。——A. F.
第七节 对实际问题的应用
236 现在,我们可以用一般的方法解决底A持续受热,同时两个无穷边B和C保持0度的一个矩形薄片BAC中的热传导问题了。
假定这个薄片BAC的所有点的初始温度均为0,但是边A的每一点的温度由某种外因保持,其固定值是从边A的端点O到点m的距离的函数f(x),边A全长r;设v是其坐标为x和y的点m的恒定温度,我们需要确定作为x和y的函数v。值v=ae-my sinmx满足方程 a和m是任意两个量。如果我们取
a和m是任意两个量。如果我们取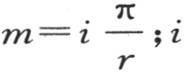 是一个整数,那么,当x=r,y可以取任一值时,值
是一个整数,那么,当x=r,y可以取任一值时,值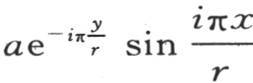 就变成0。因此,作为v的一个更一般的值,我们假定
就变成0。因此,作为v的一个更一般的值,我们假定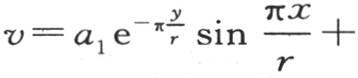
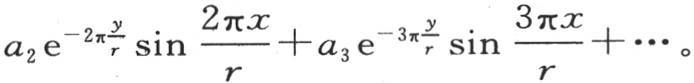
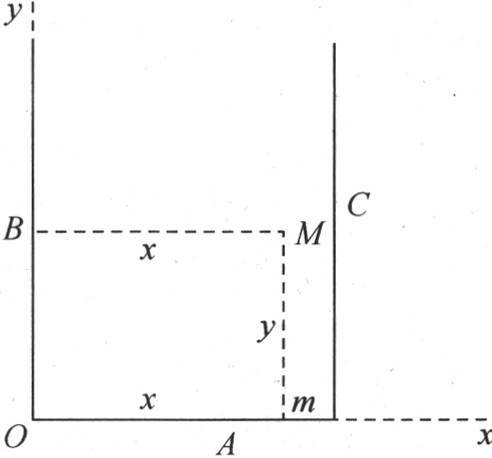
图7 【18】
如果假定y等于0,那么由假设,v的值就等于已知函数f(x),这样我们有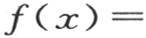

系数a1 ,a2 ,a3 …可以通过方程(M)来确定,并且,一旦把它们代入v值中,我们就有
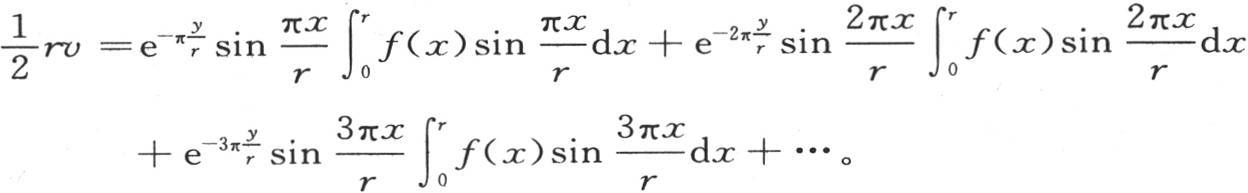
237 当在上面的方程中假定r=π时,我们得到一个形式更简单的解,即
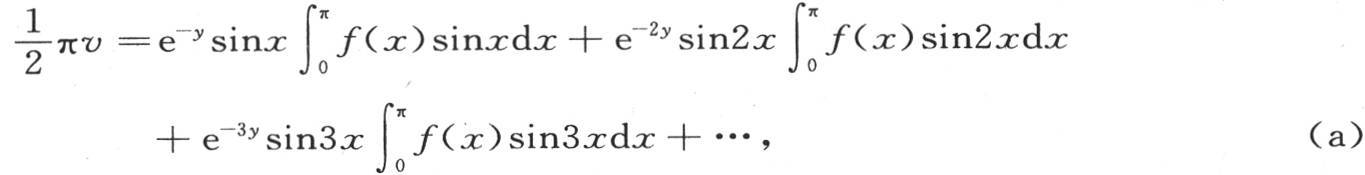
或者是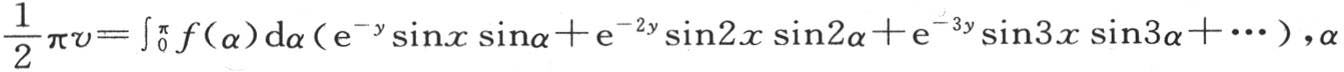 是一个新变量,它在积分后消失。
是一个新变量,它在积分后消失。
如果这个级数的和被确定,并且如果我们把它代到上一个方程中去,我们就有一个有限形式的v值。这个级数的两倍等于e-y [cos(x-α)-cos(x+α)]+e-2y [cos2(x-α)-cos2(x+α)]+e-3y [cos3(x-α)-cos3(x+α)]+…;用F(y,p)表示无穷级数e-y cosp+e-2y cos2p+e-3y cos3p+…的和,我们得到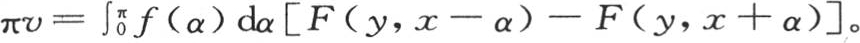 我们也有
我们也有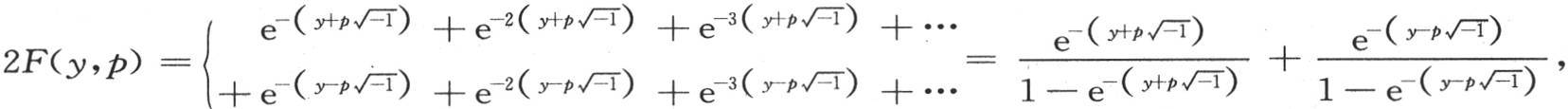 或者是
或者是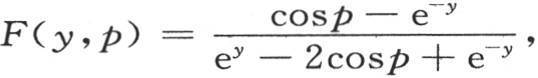 因此
因此
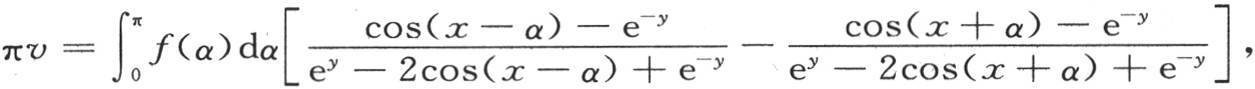
或者是
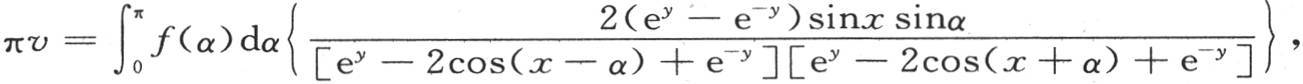
或者,当把系数分解成两个分数时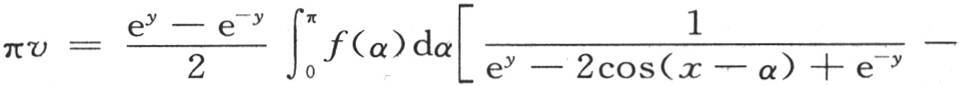
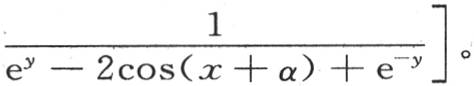
在有限形式下的实际项中,这个方程包含方程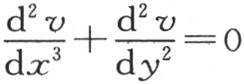 的积分,该积分适用于在端点受单一热源的恒定作用的矩形固体中的均匀热运动问题。
的积分,该积分适用于在端点受单一热源的恒定作用的矩形固体中的均匀热运动问题。
不难确定这个积分与有两个任意函数的通积分的联系;这些函数正是由于问题的性质而成为确定的,并且,当在α=0到α=π的界限内考虑问题时,除函数F(α)外,没有任何东西是任意的。在一个适合于数值应用的简单形式下,方程(a)表示简化成一个收敛级数的同一v值。
如果我们希望确定这个固体在它已经达到其永恒状态时所包含的热量,那么我们就从x=0到x=π,y=0到y=∞取积分∫dx∫dyv;其结果与所要求的量成正比。一般来说,矩形薄片中均匀热运动的性质不可能不由这个解所表示。
接下来,我们将从另一种观点考查这类问题,并确定不同物体中变化的热运动。

格勒诺布尔景

布瓦利(Louis-léopold Boily)所画两幅著名的傅立叶肖像中的一幅。布瓦利是法国大革命法兰西帝国时期的画家,一生画了5000件肖像画。

傅立叶青年时期的一幅素描肖像。作者是傅立叶在欧塞尔时的朋友克洛德·戈特罗(Claude Gautherot),一位强烈的雅各宾派成员。戈特罗是傅立叶在大革命末期被捕入狱后,在大恐怖达到顶点时,欧塞尔市派出的赴巴黎向国家公共安全委员会请求释放他的三人代表团成员之一。这幅素描现藏于格勒诺布尔市图书馆。

远征埃及时期的傅立叶。迪特尔特雷(Dutertre)约作于1800年的版画,此画现藏于凡尔赛宫。

书架上展示的为《埃及情况》(Description of Egypt, 1808—1825)。当傅立叶远征埃及时曾被这一国家的古文明所震撼。埃及研究院秘书的任职又使他更深入全面地了解到埃及的国政沿革及其文化发展。回国后他负责《埃及情况》的出版工作,他在该书绪言中介绍埃及自古至法军远征时的历史,并进行全面评述,因此傅立叶也被人称为埃及学学者。

《拿破仑一世及皇后的加冕典礼》
这幅画是奉拿破仑的命令而作,描绘的是1804年12月2日拿破仑在巴黎圣母院举行的加冕仪式。
画面中心形象是拿破仑从教皇手中接过的王冠,赐给皇后约瑟芬。罗马教皇被请来参加仪式,想借教皇在宗教上的号召力来扩大自己的影响和肯定称帝的合法权,不过只让他坐在祭坛前作为后盾而已。受加冕的皇后长长的皇袍由宫女罗席福柯拉夫人和瓦勒特夫人牵着,中间平台上坐着皇后的母亲,围绕中心周围站立着主教、王公贵族、将军、各国大使以及前来祝贺的外国国王、王后等,画中有近百人的肖像,据说很多是请真人来到画室画的。这幅画构图宏大,气势磅礴,构思巧妙,以肖像写实手法创作而成。

身着行政长官制服的傅立叶肖像。该肖像画现藏于圣·热尔曼博物馆。

伊泽尔省首府格勒诺布尔。在格勒诺布尔市,作为伊泽尔最高行政长官,傅立叶在任期间完成了在一百多年时间里历届政府多次努力都没有完成的对里昂和格勒诺布尔之间的勃格旺地区绵延约两千万英亩的大片沼泽地实施的排水工程。这是傅立叶在法国青史留名的另一个贡献。

浅浮雕展现的是傅立叶视察勃格旺沼泽地时的情景。大树前手指远方者即为傅立叶。
欧塞尔市政府大厅墙壁上的两个浅浮雕的照片。这两个浅浮雕原本装饰在该市为纪念而制作的傅立叶半身铜像的底座上,铜像坐落在欧塞尔植物园中。“二战”期间,铜像被纳粹熔化做枪炮。当时的市长让·莫罗(M. Jean Moreau)设法偷出并保存了这两个浅浮雕。

浅浮雕展现的是傅立叶在开罗宣读克莱贝尔(Jean-Baptiste Kléber)将军悼词时的情景。在拿破仑离开埃及回国后,克莱贝尔是埃及远征军统帅的继任者。1800年6月,克莱贝尔遭暗杀身亡。位于浮雕中心位置的即为傅立叶。

欧塞尔伯爵宫,墙壁上镶嵌欧塞尔各个时期的名人像,下排的第二个为傅立叶的雕像。

伯爵宫墙壁上的傅立叶雕像


约瑟夫·傅立叶大学校园景。大学的创建可以上溯至1339年,当时设有医科、七种自由艺术及法律等学科。1811年由傅立叶建立了理学院;1841年设立了医科及制药学预科学校;20世纪50年代建立了许多大型研究机构;1962年建立了医科及制药学学院;1971年组建格勒诺布尔理科及医科第一大学,1987年更名为约瑟夫·傅立叶大学。

为了纪念傅立叶,法国巴黎有条街道以“傅立叶”命名。图为该街道的指示牌。

贝尔拉雪兹公墓的傅立叶墓

傅立叶是古斯塔夫·埃菲尔刻于埃菲尔铁塔上的72个学者名字之一。


法国科幻作家儒勒·凡尔纳在他的《奇异的旅行》作品集中几次提及傅立叶的热的实验和理论。

傅立叶变换红外光谱仪。傅立叶的数学成就广泛应用于光学领域,因此,有几种光学仪器都是以“傅立叶”来命名的。
注释
【1】 即沃利斯所得到的π的表达式: ——译者注
——译者注
【2】 根据第4节的方法,用cosy,cos3y,cos5y等等分别乘第一个方程两边,可以确定系数a,b,c,等等,正如格雷戈里(D. F. Gregorg)所做过的。《剑桥数学学报》(Cambridge Mathematical Journal),第1卷,第106页。——A. F.
【3】 和在第222目中一样,这可以通过从0到π的积分推出。——R. L. E.
【4】 参见德·摩根(De Morgan)的《微积分计算》(Diff. and Int. Calculus),第605—609页。——A. F.
【5】 在英文版中,此式中的各项没有 这些系数,此处是根据法文《文集》本添加的。——汉译者
这些系数,此处是根据法文《文集》本添加的。——汉译者
【6】 格雷戈里从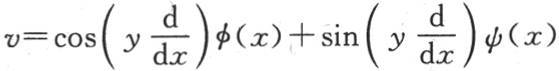 的形式得出这个结果。《剑桥数学学报》,第1卷,第105页。——A. F.
的形式得出这个结果。《剑桥数学学报》,第1卷,第105页。——A. F.
【7】 在英文本中,下面两式右边的系数不是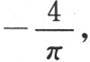 而是-2,此处依法文《文集》本改定。——汉译者
而是-2,此处依法文《文集》本改定。——汉译者
【8】 此式中的A2 ,在英译本中是“A”,此处根据法文《全集》来修改。——汉译者
【9】 在英译本中,这些方程的左边第一项,在英译本中,都是“A”,此处根据法文《文集》本校订。——汉译者
【10】 在法文本和英译本中,表示b和d的方程的右边第三项c的系数的第二项中,分子π2 都是π4 ,这与这些式子中所体现的规律相悖。傅立叶1807年的研究报告以及法文《文集》的相应分子都是π2 ,因而这里以后两个版本改定。——汉译者
【11】 拉格朗日(Lagrange)已经表明(Miscellanea Taurinensia,第三卷,1766年,第260—261页)。由方程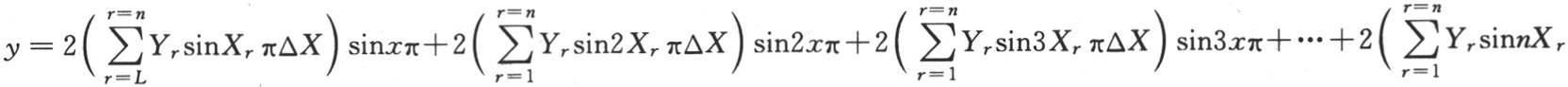
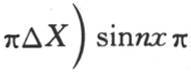 所给出的函数y,对应于x的值X1 ,X2 ,X3 ,…Xn ,得到值Y1 ,Y2 ,Y3 ,…Yn ,此处
所给出的函数y,对应于x的值X1 ,X2 ,X3 ,…Xn ,得到值Y1 ,Y2 ,Y3 ,…Yn ,此处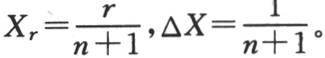
然而,拉格朗日不作从这个求和公式到由傅立叶所给出的求积公式的变换。
参见黎曼的《数学全集》(Gesammelte Mathematische Werke),莱比锡,1876年,第218—220页,他的历史性评论,“论利用三角级数表示函数”(Ueber die Darstellbarkeit einer Function durch eine Trigonometrische Reihe)。——A. F.
【12】 任意地处在某个界限内的函数,可以以余弦级数展开的情况,以及可以以正弦级数展开的情况,已由汤姆森(W. Thomson)爵士在一篇签字为P. Q. R. 的论文“论傅立叶的三角级数中的函数展开式”〔(On Fourier's Expansions of Functions in Trigonometrical Series),《剑桥数学学报》,第258—262页〕中表明。——A. F.
【13】 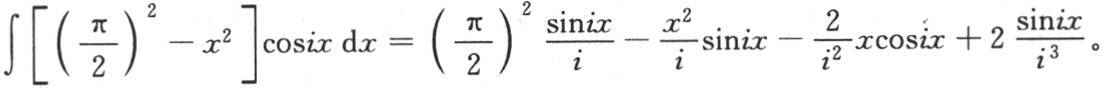 ——R. L. E.
——R. L. E.
【14】 以0到π的界限之间的余弦来表示,则为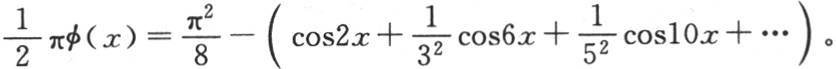 参见德·摩根的《微积分计算》,第622页。——A. F.
参见德·摩根的《微积分计算》,第622页。——A. F.
【15】 泊松(Poisson),德弗勒斯(Deflers),狄利克雷(Dirichlet),德克森(Dirksen),贝塞尔(Bessel),哈密尔顿(Hamilton),布尔(Boole),德·摩根,斯托克斯(Stokes)等已经提供了一些证明,见第195—196页的注。——A. F.
【16】 奥金尼利(J. O'Kinealy)先生已经表明,如果我们设想,对于连续区间λ上的x的每一个变程,任意函数f(x)的值都循环,那么我们有符号方程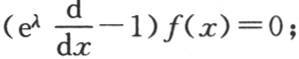 因这个辅助方程的根是
因这个辅助方程的根是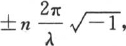 n=0,1,2,3…∞,由此得到
n=0,1,2,3…∞,由此得到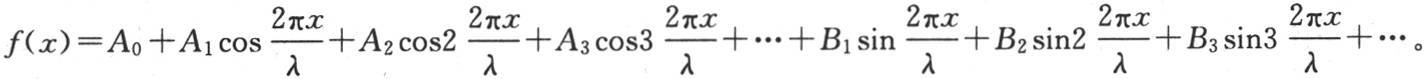
这些系数在傅立叶的方法中通过用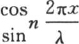 乘两边,并从0到λ积分而确定。[《哲学杂志》(Philosophical Magazine),1871年8月,第95、96页。]——A. F.
乘两边,并从0到λ积分而确定。[《哲学杂志》(Philosophical Magazine),1871年8月,第95、96页。]——A. F.
【17】 我们有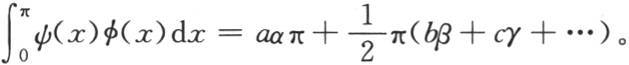 ——R. L. E.
——R. L. E.
【18】 此图在英译本中没有,但在法文《文集》本中是有的,我们因而在此添上。——汉译者
