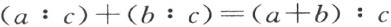补篇Ⅱ　比例论建立的简化

在第三章§14～§16里，不用阿基米德公理即根据公理Ⅰ_1～3 ，Ⅱ～Ⅳ所建立起来的比例论还可以简化。

以下我们利用§15开始所引进的线段、线段相等、线段的和的记法以及那里所提出的结果：关于线段加法的结合律和交换律都成立。

现在我们规定线段a ，b 的比a :b 。在一个以a ，b 为两个直角边的直角三角形里，用直角边a 相对的角（在合同意义下是唯一确定的）规定为a :b 。如果用a :b 和c :d 所规定的两个角合同，则说这两个比相等，而且在这种意义下也写作一个“比例式”a :b ＝c :d 。所以立即推得每一个线段比和它自身相等，两个线段比若和第三个比相等，则原来两个比彼此相等，且有：如果a ＝c ，b ＝d ，则a :b ＝c :d 。

根据三角形的角和定理，也可推得：如果a :b ＝c :d ，则b :a ＝d :c 。再者利用公理Ⅲ和Ⅳ可得以下定理（补图1）：如果a :b ＝c :d ，则a :b ＝（a ＋c ）:（b ＋d ），而且根据外角定理，如果a :b ＝a :c ，则b ＝c 。特别是从最后一个定理可以推出：对于三个线段a ，b ，c ，只有一个第四比例项，即在方程a :b ＝c :x 中对x 只能有一个解，从角的迁移的可能性连同平行公理可以推得第四比例项的存在。

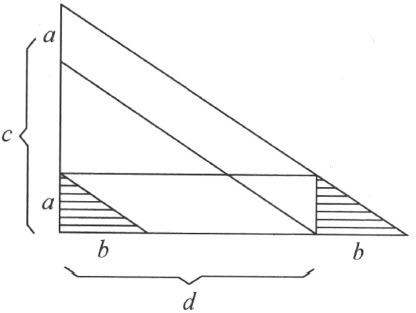
补图　1

比例内项的可换定理，即如果a :b ＝c :d 则a :c ＝b :d 。它的证明可如下得出。考虑两个直角三角形，它们的直角边分别是a ，b 和c ，d ；而且有这样的位置：第二个三角形的直角边c 位于第一个三角形过直角顶的直角边b 的延线上，同样地，d 位于a 的延线上（补图2）。根据所假设的比例，利用圆周角相等对等弧定理或其逆定理得出：两条斜边的四个端点共圆。根据这个定理，再考虑以a ，c 和b ，d 为直角边的两个三角形就能得出a :c ＝b :d ^（1） 。

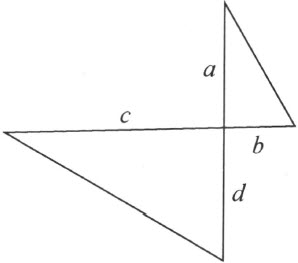
补图　2

从比例内项的可换性，我们特别地得到比例合成的可能性：如果a :b ＝a ′:b ′且b :c ＝b ′:c ′，则a :c ＝a ′:c ′。即从给出的比例经过内项交换可得a :a ′＝b :b ′＝c :c ′，因而a :c ＝a ′:c ′。

利用第四比例项的存在也可得出下列的第二个合成规则：如果a :b ＝b ′:a ′且b :c ＝c ′:b ′，则a :c ＝c ′:a ′。这是因为如果u 是a ，b ，c ′的第四比例项，即有a :b ＝c ′:u ，则根据上面假设，应有c ′:u ＝b ′:a ′，即c ′:b ′＝u :a ′，而且u :a ′＝b :c 再由c ′:u ＝a :b 和u :a′ ＝b :c （依照前面所说的比例的合成规则）即得c ′:a ′＝a :c 。

现在证明比例论的基本定理：如果两条平行线在任意角的两边上分别截取线段a ，a ′和b ，b ′，则比例a :a ＝b :b ′成立。要得到证明，只要利用三角形角的平分线共点这个定理（如同§16定理41的证明）。现在把这条定理应用到三角形OAB 和OA ′B 上，这里O 是所考虑角的顶点，A ，B 和A ′，B ′分别是二平行线和角的两边的交点；再设OA ＝a ，OB ＝b ，OA ′＝a ′，OB ′＝b ′（补图3）。设S 和S ′分别是三角形OAB 和OA ′B ′角平分线的交点。于是S 到直线OA 和OB 有等距离r ，且S ′到这两条直线也有等距离r ′。我们将证a :a ′＝r :r ′，同理有b :b ′＝r :r ′，于是论断即得以证明。

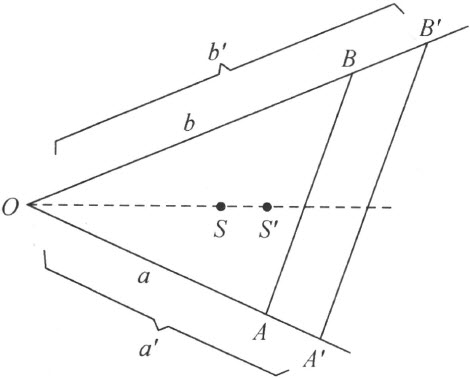
补图　3

要证明比例a :a ′＝r :r ′，我们考虑三角形OAS 和OA ′S ′，这里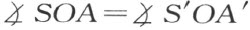 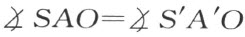， ，而且这两角都是锐角（因为是一角之半）。设D 和D ′分别是由S 和S ′向直线OA 所作垂线的垂足，且分别落在线段OA 和OA ′的内部。OA 和OA ′被D 和D ′分别分成两个线段u ，υ 和u ′，υ ′。于是就有

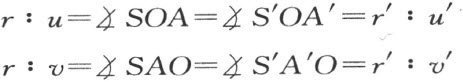
因此

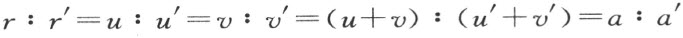
亦即

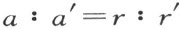
应用比例论的基本定理，特别是希尔伯特称为巴斯噶定理的命题可以化为上述的比例第二合成规则。这条定理（§14定理40）是：设A，B，C 和A′，B′，C′ 分别是二相交直线上的三个点，而且它们都不同于这二直线的交点，于是若BC′ 平行于CB′ ，而且CA′ 平行于AC′ ，则AB′ 平行于BA′ 。将线段OA ，OB ，OC 分别记作a ，b ，c ；将线段OA′ ，OB′ ，OC′ 分别记作a′ ，b′ ，c′ ，则按照比例论的基本定理，上面的假设等价于两个比例

而且结论等价于比例

然而这一比例也可以从上面的两个利用第二合成规则得出。

这样不用线段的乘法建立的比例论只要固定一条单位线段e 就能引进线段乘法。实际上，我们可规定e ，a ，b 的第4比例项是线段a ，b （就单位e 而言）的乘积。

关于这样规定的线段乘法的运算律是这样的：乘法交换律是由比例内项的可换性得出。乘法结合律陈述为：如果e :a ＝b :u ，e :b ＝c :υ ，e :u ＝c :ω ，则e :a ＝υ :ω 。这个算律可以如下证明。由所假设的第二个比例得b :e ＝υ :c ，连同所假设的第三个比例再应用一个合成得b :u ＝υ :ω 于是根据所假设的第一个比例即得e :a ＝υ :ω 。乘法分配律陈述为：如果e :a ＝b :u ，e :a ＝c :υ ，则e :a ＝（b ＋c ）:（u ＋υ ）。要想证明它，只需证明：如果b :u ＝c :υ ，则b :u ＝（b ＋c ）:（u ＋υ ）。但按照在开始时所提及的一条定理，这个论断是正确的。

在这样引进线段计算之后，现在就可以如同§17里所讲的一样建立平面解析几何。

注记 　利用单位线段来代替定义线段乘法为建立解析几何，必须引进比的计算。先用下面的规则来规定比的加法和乘法：

^（2）

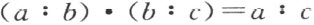
于是等比加等比仍得等比，等比乘以等比仍得等比。

从前面所建立的比例论的性质，特别是从第四比例项的存在，这些规则均能适合，而且加法及乘法的其余规则也均成立。在没有其他注解的情况下，我们可以得出：乘法的逆运算即除以a :b 就是乘以b :a ，而且比a :a （＝b :b ）起着乘法恒等元的作用。

————————————————————

（1） 这个证明的思路取自恩立克（F. Enriques）的教本《初等几何问题》（Fragen der Elementargeometrie）。

（2） 用两线段比之和作为两确定角之和是不合适的，即由角的几何加法的规定它与以下事实相违背，因为由线段的比所确定的角常是锐角，而两锐角之和却不常常是锐角。