第6章　论起折射和反射作用的透明体的形状

我将在这里给出一种简易而自然的采取同样原理的实用图形推导方法。通过折射或反射，这些图形可以根据需要发散或汇集光线。

土星环上的卡西尼环缝。

在阐明了如何根据我们关于不透明体和透明介质性质提出的假设得到反射和折射的特性之后，我将在这里给出一种简易而自然的采取同样原理的实用图形推导方法。通过折射或反射，这些图形可以根据需要发散或汇集光线。尽管到目前为止我还没有看到利用折射图形的工具，这不仅因为按照这些图形以必需的精度加工望远镜片有困难，而且还因为折射本身存在着一种妨碍光线完好一致的性质，牛顿先生已用实验作了充分的证实，我也不愿放弃这一发现，可以说因为它表现了它的特征，还因为它发现了折射光线与反射光线的统一描述，进一步证实了我们的折射理论。还有，将来或许有人会找到目前尚未发现的用途。

为了着手讨论这些图形，先假设需要找到一个表面CDE，它把来自A点的光线汇聚到点B（图42）。而该表面的峰为直线AB上的给定点D。我认为无论折射还是反射，只要使表面像这样，从A点到曲线CDE上的各点，再从这些点到聚焦点的光程（这里的光程是直线AC和CB，直线AL和LB，以及直线AD和DB）的传播时间相等。运用这个原则求这些曲线就变得容易了。

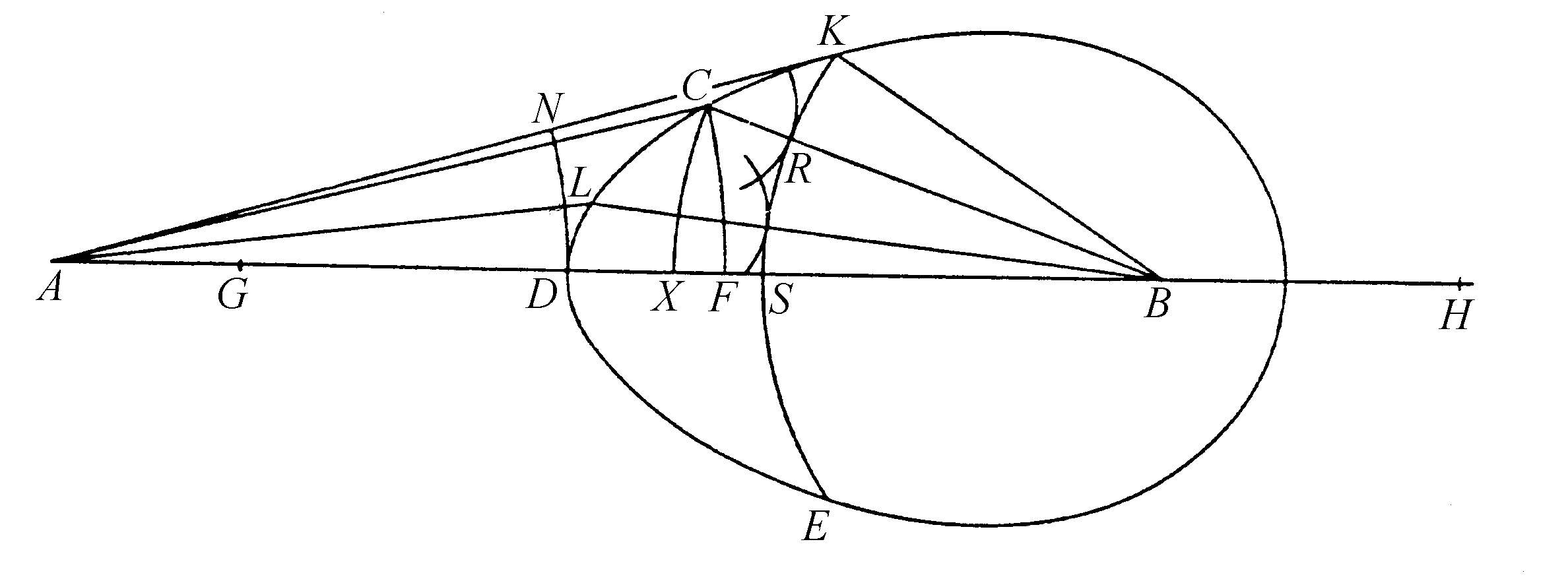图42

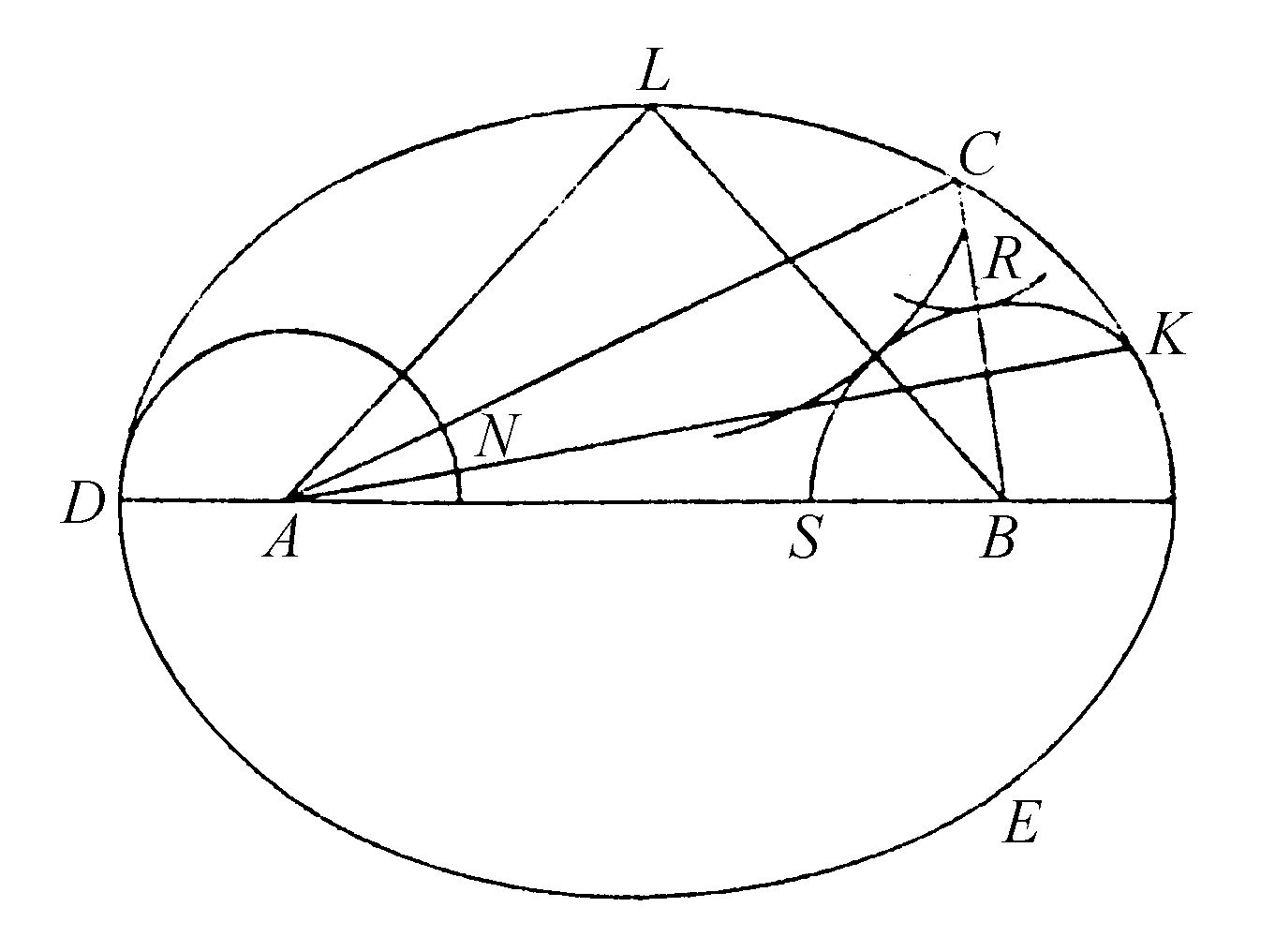图43

对于反射表面，因为直线AC与CB的和应该等于AD与DB的和，显然DCE应当是一个椭圆（图43）。而对于折射，假定已知介质A与B中的光速比，例如为3比2（如我们所知，这与折射中的正弦比是一样的），只需作DH等于DB的 ；并以A点为中心画段弧FC，与DB相交于F。再以B点为中心，以等于FH的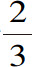 的BX为半径，画另一段弧。两段弧的交点为所求的曲线应该通过的那些点中的一个。因为该点是按这种方法找到的，很容易立即证明沿AC、CB所需要的时间等于沿AD、DB所需要的时间。

假定直线AD表示光在空气中经过这段距离AD所需要的时间，显然，等于DB的 的DH，表示光在介质中沿DB所需要的时间，因为随着速度减小，所需要的时间成比例增加。于是，整个直线AH，将表示沿AD、DB所需要的时间。同样，直线AC或AF表示沿AC所需要的时间。等于CB的 的FH，表示在介质中沿CB所需要的时间。因此，整条线AH表示沿AC、CB所需要的时间。由此可见，沿AC、CB所需要的时间等于沿AD、DB所需要的时间。同样可以证明，如果L与K是曲线CDE上的另外的一些点，那么沿AL、LB所需要的时间以及沿AK、RB所需要的时间，也总是用直线AH所表示。于是，等于上述沿AD、DB所需要的时间。

为了进一步地证明通过这些曲线旋转形成的表面，使所有自A点到达它们的光线，以同样的方式趋向B点，假定曲线上有一点K，距离D比C远些，以致直线AK落在从外部折射的曲线上（图44、45）。以B点为中心作弧KS，它与BD相交于S，与直线CB相交于R。再以A点为中心作弧DN，与AK相交于N。

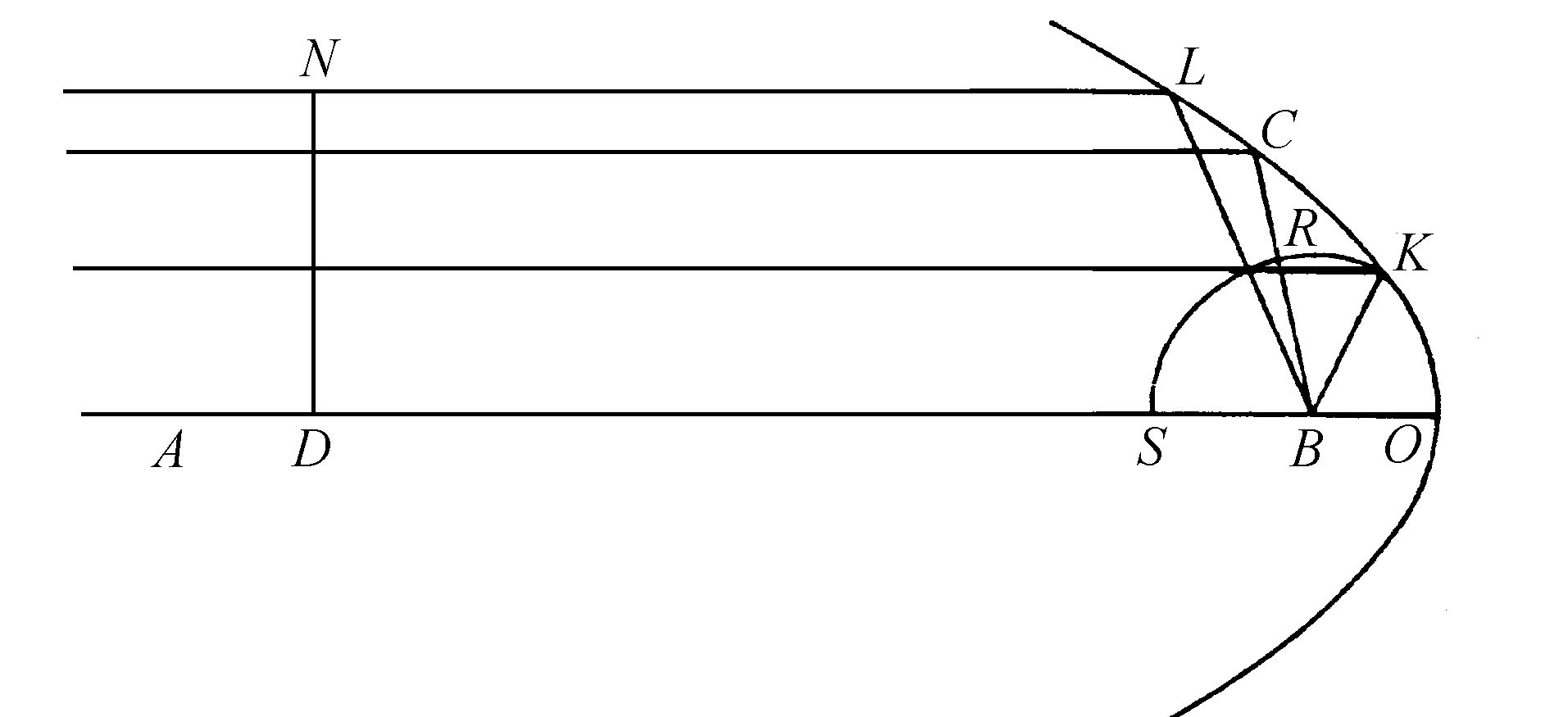图44

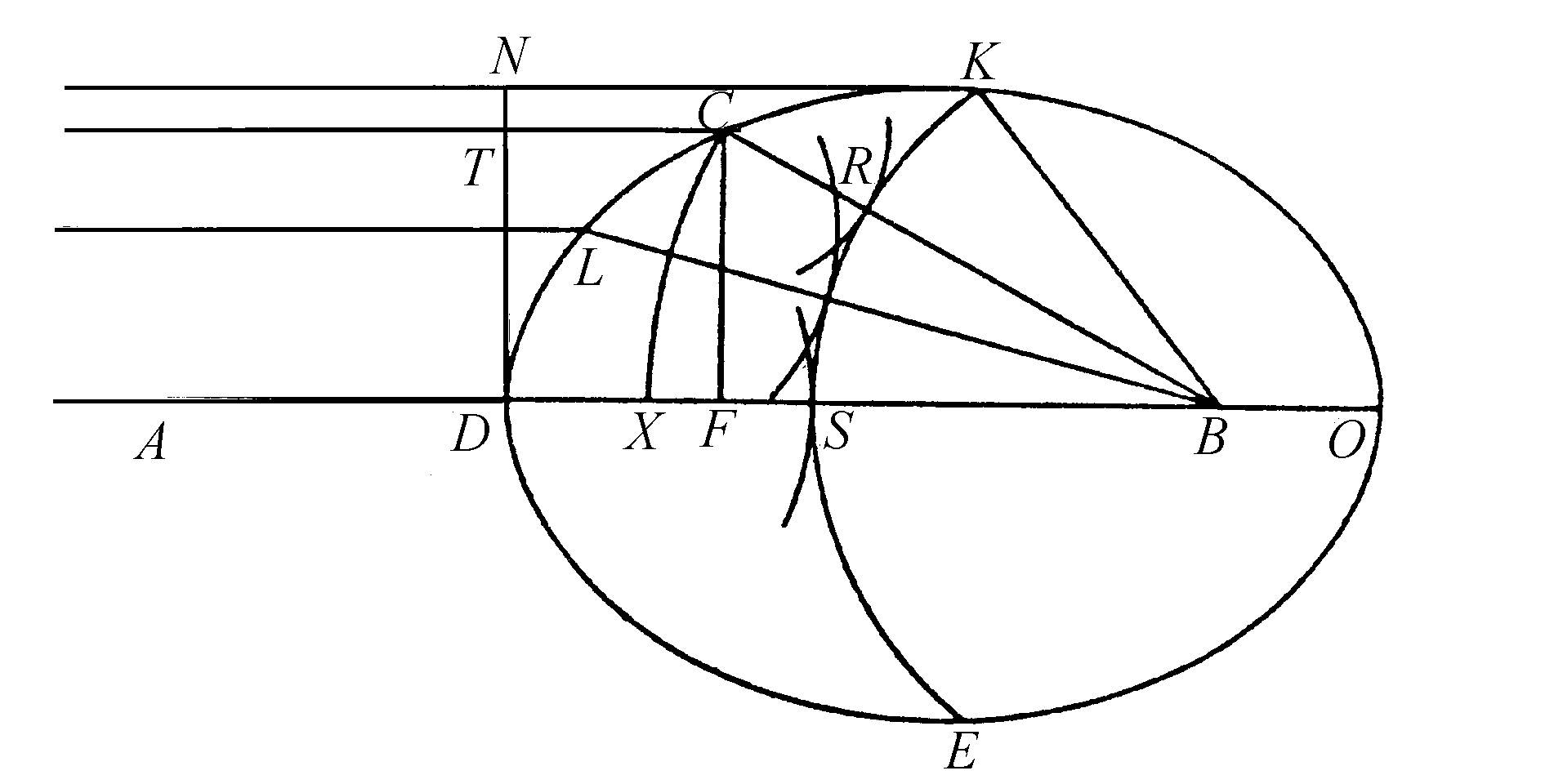图45

因为沿AK和KB所需要的时间，等于沿AC和CB所需要的时间，如果从前者扣除沿KB的时间，并从后者扣除沿RB的时间，那么剩下来沿AK的时间等于沿AC和CR两部分的时间。因此，光沿AK传播的时间里，它也沿AC传播并且又以C为中心以CR为半径在介质中形成了一个球面分波。因为CB与圆周KS正交，所以该分波与此圆周相切于R。同样地，如果人们考虑曲线上的另一点L，得到当光沿AK传播时，它也沿AL传播并又以L为中心形成一个与上述圆周KS相切的分波。曲线CDE上的其他所有点都是如此。那么，在光到达K点时，弧KRS将包络自A点出发经过DCK的传播的光运动。因此，这段圆弧构成由A点发源的波在介质中的传播；可以由弧DN，或者由其他离中心点A更近的弧来表示。而弧KRS上的各个部分将顺序沿垂直于它们的直线传播，也就是说，沿趋向中心B的直线传播（可以用我们以上证明球面波是沿来自其中心的直线传播的这一方法来证明），并且正是波的各个部分的光程本身构成了光线。显然：所有这些光线都趋向于B点。

也可以用下述方法来决定用作折射的曲线上的C点和其他所有点：在G点分割DA，使DG等于DA的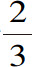 ；以B点为中心，作圆弧CX，与BD相交于X；再以A为中心作另一圆弧，半径AF等于GX的 ；或说得确切些，如上述作了圆弧CX之后，只需要作直线DF等于DX的 ，再以A为中心画出弧FC；显而易见，这两种构造方法都将回归于我们前面所讲的第一种方法。并且通过后一种方法可以看到，这些曲线正是笛卡儿先生在他的《几何》中称做的第一类卵形曲线。

在这种卵形曲线中只有其中的一部分适用于折射即DK，如果AK是切线，K是终点。至于其他部分，笛卡儿指出，如果有某种特性能使光强（或者，我们应当说是光速，但他不会这么说，因为他认为光的运动是瞬时的）按3比2的比例增加的材料制成镜面，那么它可以用于反射。但是我们曾经证明，在我们关于反射的解释中，镜面的物质是不可能产生这一现象的，它完全是不可能的。

从有关这种卵形曲线的论证出发，很容易找到一种图形将平行入射线汇聚到一点。采取同样的考虑，如图46所示，只是假定A在无穷远处发出平行的光线，卵形曲线就变成了正椭圆，其图形同卵形曲线没有什么两样，只是先前为圆周上一段弧的FC，在这里变成了一条垂直于DB的直线。因为光波DN也同样由一条直线表示，不难看出这一波上所有点沿平行DB的直线传播到表面KD，然后朝向点B并于同一时刻到达那里。至于用作反射的椭圆，显然它在这里变成了一条抛物线，因为它的焦点A可以被视为与另一个焦点B相距无穷远，B就是这条抛物线的焦点，所有平行于AB的光线的反射线都趋向它。这些效应的证明与前面的证明一样。

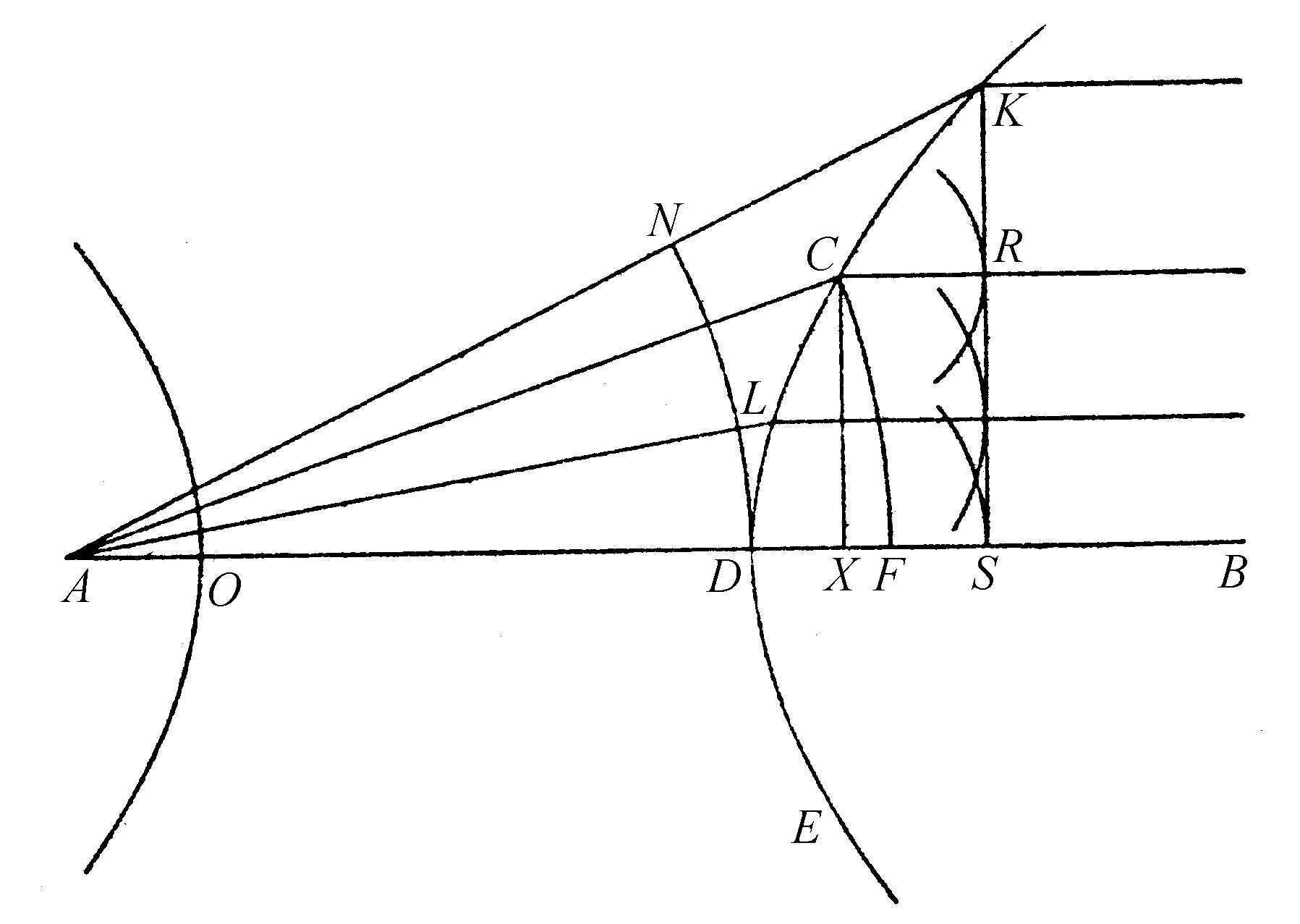图46

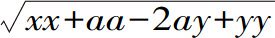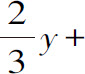
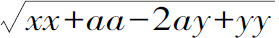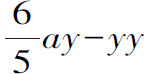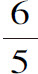通过代数计算很容易得到，用于折射的曲线CDE是一个椭圆，它的长轴半径与焦距之比为3比2，即折射比。给定DB为a，它的未确定的垂线DT为x，TC为y；则FB为a—y；CB为 。而曲线的性质要求TC的 与CB之和等于DB，正如在上述图形中所要求的那样，因而方程式应为 等于a。这一方程简化后为 等于 。也就是说，作了DO等于DB的 后，DF与FO的乘积将等于FC平方的 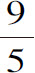倍。由此可见，DC是一个椭圆，其轴DO与特性参数之比为9比5；于是DO的平方与焦距的平方之比为9比9-5即9比4，因此DO与焦距之比为3比2。

此外，如果假定B点在无穷远，我们会发现CDE不再是第一类卵形曲线而是一个正抛物线，它使来自A点的光线变得平行。结果，那些在透明体内平行的光线在外面汇聚于A点。必须注意，CX与KS变成了垂直于BA的直线，因为它们表示中心在无穷远处的圆上的弧。垂线CX与弧FC的交点为C点，这一点是曲线所应该通过的点。同理，光波DN上的所有部分到达表面KDE之后，平行地同时到达KS直线。它的证明同第一类卵形曲线的证明一样。另外，同前面同样简单的计算发现，这里的CDE是一个抛物线，其轴线DO等于AD的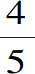 ，特性参数等于AD。由此，很容易证明出DO与焦距之比为3比2。

这是圆锥曲线用于折射的两种情形，同笛卡儿在他的《屈光学》（Dioptrique）中所作的解释一样，他首先发现了关于折射中这些曲线的用途，以及我们刚才讨论的第一类卵形曲线的用途。第二类卵形曲线适用于汇聚于一给定点的光线，在这种卵形曲线中，如果接受光线的表面的顶点为D，那么另一个顶点将位于B和A之间，或者落在A点以外，其具体位置依据AD与DB之比值的大小而定（图47）。后一种情形，与笛卡儿称做第三类卵形曲线中的情形相同。

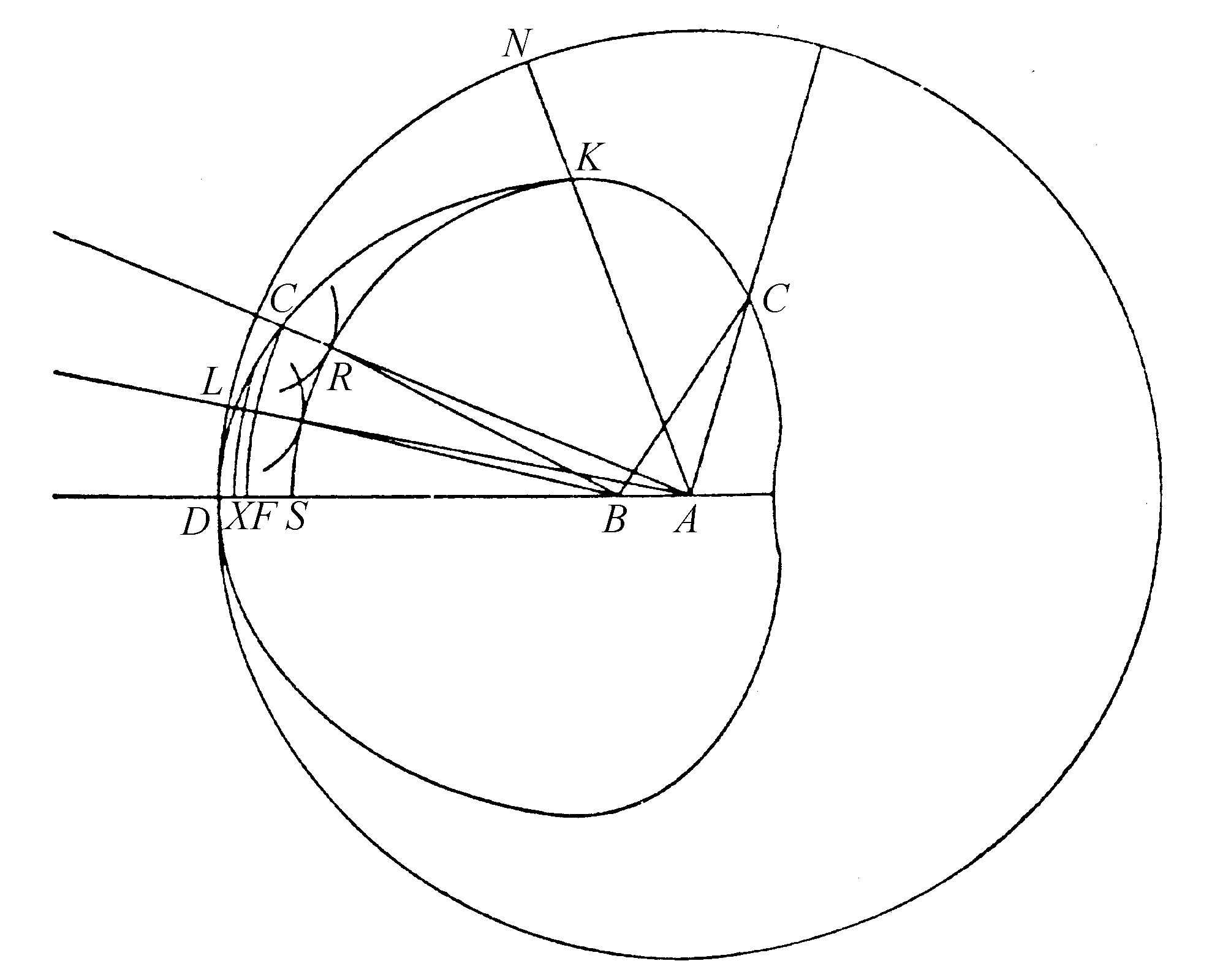图47

第二类卵形曲线的求解和图形与第一类卵形曲线的情况相同，其作用的证明也相同。不过值得注意的一点是，这一类卵形曲线在一种情形下将变成为完全的圆，即当AD与DB的比和折射比相同时。在这里该比值应如我在很久以前所观察到的那样为3比2。第四类卵形曲线能运用于一些不可能存在的反射，没有必要提出来了。

至于笛卡儿先生发现这些曲线的方法，由于他本人没有对此作过说明，在我所知道之前也没有谁对此作过说明，因而在这里我顺带提一下我对这一点的看法。假定我们想要找一个由曲线KDE旋转而成的表面，使从A点入射的光线转向B点。那么考虑已知的另一条这样的曲线，它顶点D在直线AB上（图48）。用G、C、F等点将它分割成无穷多小段，从这些点向A点作直线，表示入射光线。再从这些点向B点作另外的直线，然后以A点为中心画弧GL、CM、FN、DO，它们与来自A点的光线在L、M、N、O等点相交。通过点K、G、C、F，画弧KQ、GR、CS、FT，它们又与传播向B点的光线在Q、R、S、T等点相交。又假定直线HKZ与该曲线在K点相交。

图48

那么如图49，AK为入射光线，KB则为它在介质内的折射线，依据笛卡儿先生所知道的折射定律，必定可以得到角ZKA的正弦值与角HKB的正弦值之比为3比2，这一比值就是玻璃的折射比。确切地讲，角KGL的正弦值与角GKQ的正弦值之比，应该等于该比值，这里已考虑到KG、GL、KQ短小而认为它们是直线。如果GK取为圆的半径，这些正弦值就是KL与GQ。于是，LK与GQ之比就为3比2；MG比CR、NC比FS、OF比DT也是同样的比值。那么所有前者之和与所有后者之和的比，也应当等于3比2。通过延长弧DO与AK相交于X，KX就是前者的和。延长弧长Q与AD相交于Y，后者的和就是DY。于是KX与DY之比就应该等于3比2。由此可见，曲线KDE有以下性质，即从曲线上某一点，譬如K，作直线KA和KB、AK超出AD的部分与DB超出KB的部分之比为3比2。可以类似地证明在这条曲线上任意取另外一点，譬如G，AG超出AD的部分VG，与BD超出DG的部分DP之比，也为同样的比值3比2。通过这一原则，笛卡儿先生在他的《几何》中构造出了这些曲线，并且他还很容易地认识到，在平行光情形下这些曲线将变成为抛物线与椭圆。

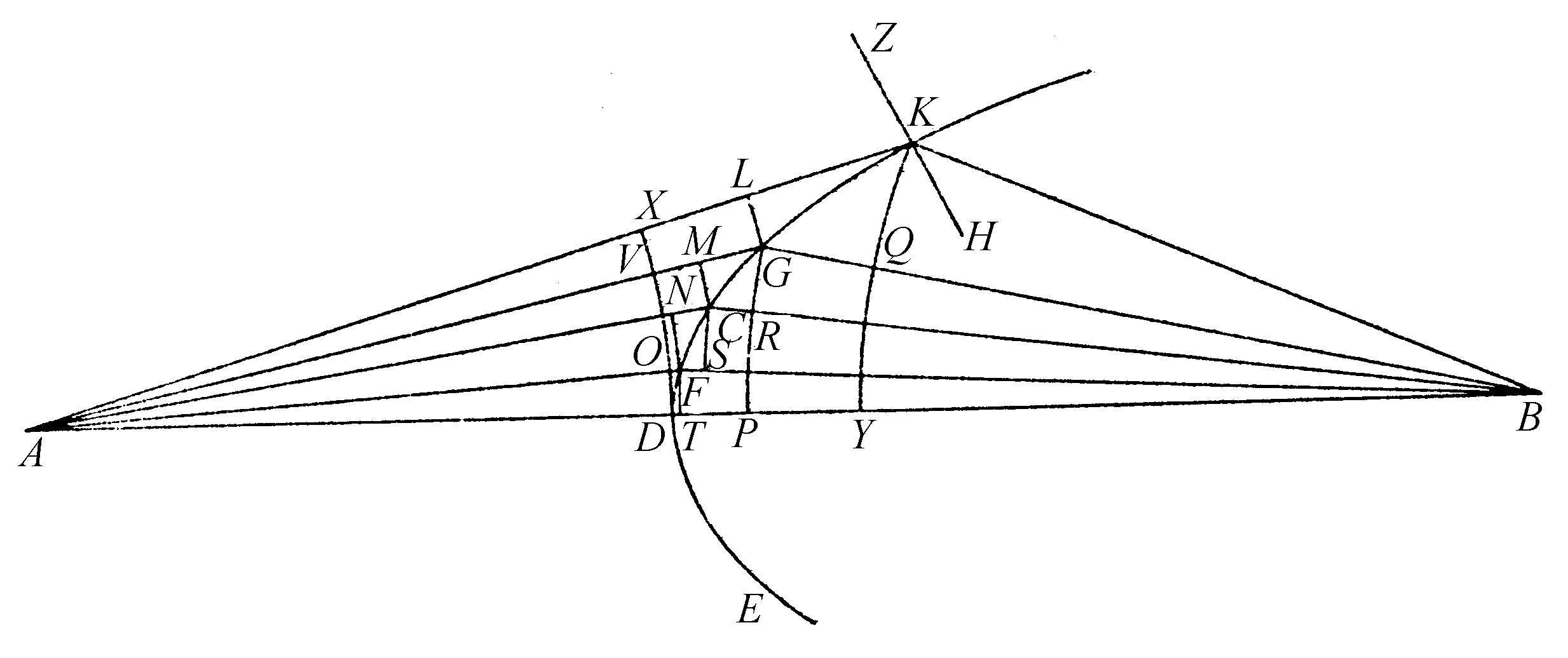图49

现在，让我们回到我们自己的方法上，并看一看，当玻璃的一边为给定图形时，另一边所要求的曲线是如何通过我们的方法毫无困难地找到的。这一给定图形不仅可以是平面，球面或者某一圆锥截面（这是笛卡儿提出该问题时所给出的限制，他把这一问题的解决留给了后人），而且还可以是完全任意的图形，也就是说，通过旋转任意给定曲线所得到的图形，对于给定曲线，人们只需要知道如何画出它的切线就可以了。

如图50，假定给定图形是通过某一曲线AK绕轴AV旋转而得到的，并且玻璃在这一边接收到来自L点的光线。此外，假定玻璃中部的厚度AB为已知，并且我们要求光线完全汇聚在点F上，无论发生在表面AK上的第一次折射如何。

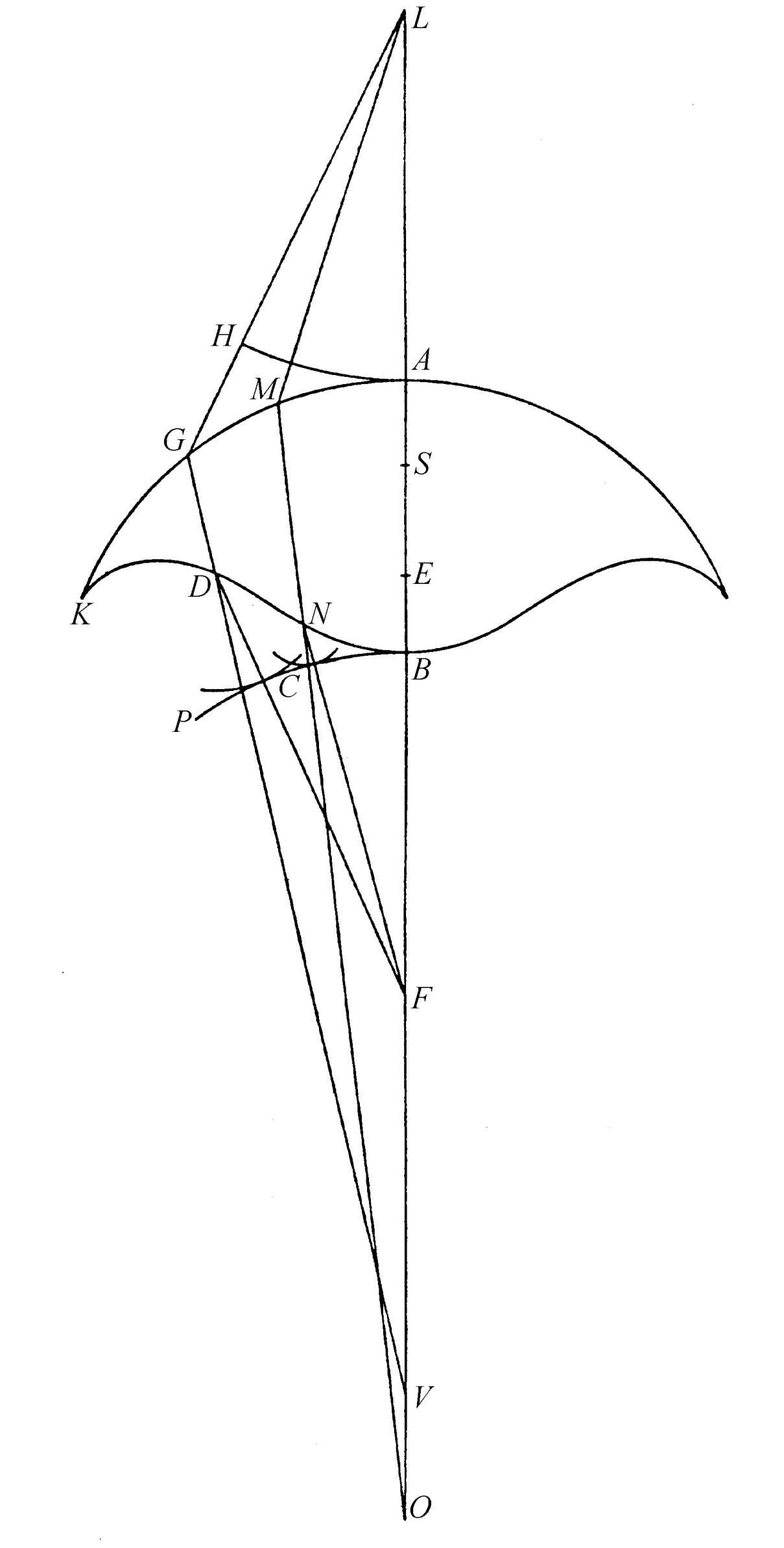图50

我认为这一问题的唯一要求是构成另一表面的周线BDK应当这样：光线从L点到表面AK，再从那里到表面BDK以及再到点F的行程应当处处时间相等，并且在每一情形下所需要的这一时间都等于光沿直线LF穿过所需要的时间，而直线LF的AB部分位于玻璃之中。

假定LG是照在弧AK上的一束光线。它的折射线GV将由过G点作出切线来确定。GV上的点D必须满足FD加上DG的 ，再加上直线GL，等于FB加上BA的 ，再加上直线AL。很清楚，它们的和是一个给定的长度。确切地讲，从其中减去已知的LG的长度之后，只需要在VG的范围内调整FD，使得FD与DG的 之和等于一个给定直线的长度就可以了。这是一个简明的问题：D点是曲线BDK应该通过的那些点之一。同样，画出另外一束光线LM，找出其折射线MO之后，在这一直线上可找到点N，如此下去进行所需要的次数。

为了证实这一曲线的作用，以L为中心画一圆弧AH，与LG相交于H；以F为中心画圆弧BP，再在AB上作AS等于HG的 ；作SE等于GD。考虑到AH是L点发源的光波，A点的光波必定在它从H段到达G点的时间里，沿AS进入透明体。如上所述，假定折射比为3比2。我们知道从G点入射的光波从那里沿线GD传播，因为GV是光线LG的折射线。因为GD与SE相等，在光波由G点到达D点的时间里，位于S点的另一段光波将到达E点。但当后者由E点传播到B点时，位于D点的那段波就已经将它的分波传播到空气中，分波的半径DC（假定分波与DF相交于C点）等于EB的 ，因为介质外的光速与介质内的光速比为3比2。于是很容易证明，这个光波与弧BP在点C相切。由于在作图中，FD＋ DG＋GL等于FB＋ BA＋AL；减去相等的量LH与LA，那么余下的量FD＋ DG＋GH等于FB＋ BA。又从一边减去GH，从另一边减去与之相等的 AS，余下的量FD＋ DG就等于FB＋ BS。而 DG又等于 ES，因此FD就等于FB与 BE之和。同时DC等于 EB，从两边减去这些相等长度后，余下的CF等于FB。由此显而易见，当光线从L点沿LB到达B点时，半径为DC的那个波，将同时与弧BP相切。可以类似地证明在这一时刻顺着其他光线，譬如LM、MN传播的光运动到达弧BP。由此可以得出，正如经常说到的，穿过玻璃厚度以后的光波AH的传播，为球面波BP，上面的各段将沿直线即光线，向中心点F传播。这一点已得到证实。同样，这些曲线在所有可能假定的情况下都能被找到，将在我附加的一两个例子中得到充分证实。

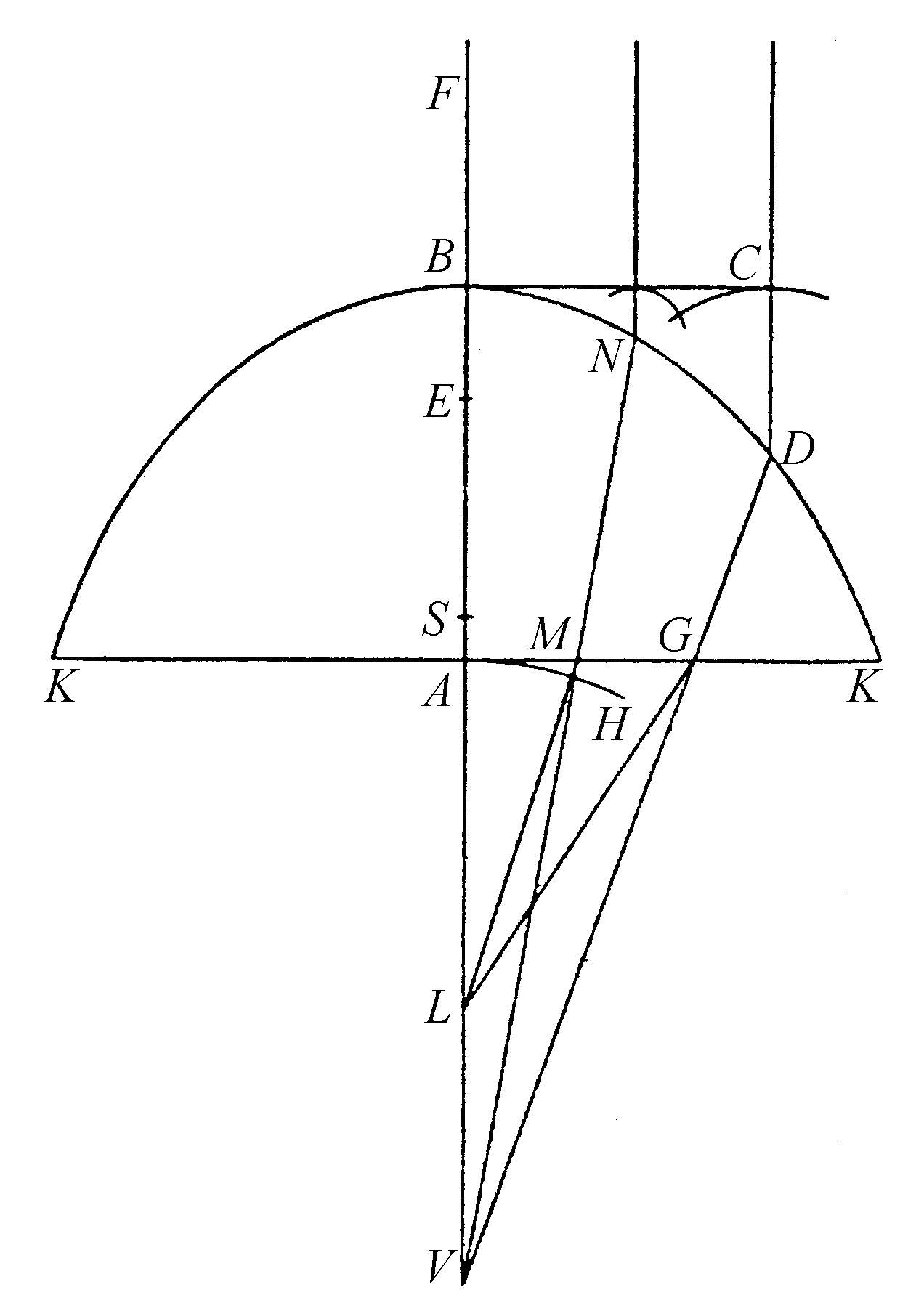图51

如图51，设有一个给定的玻璃表面AK，它是由曲线AK绕轴BA旋转而成的，其中AK可以是直线也可以是曲线。又设轴上有一给定的点L。玻璃的厚度BA也给定；需要求的是另一个表面KDB，它能将其接收到的平行于AB的光线偏转，使得它们在给定表面AK再次折射后能全部汇聚到L点。

从点L向给定直线AK上的某一点作直线LG，并把它看作一束光线，那么可以求出它的折射线GD。并且当这条线沿一边或者另一边延长后，与直线BL相交，其交点在这里为V点。又作AB的垂线BC，由于我们假定了光线互相平行，所以它表示来自无穷远点F的光波。光波BC上的各部分将同时到达L点，更确切地说，发源于L点的光波的各个部分，将同时到达直线BC。为此，必须在线VGD上找到点D，使得在作了DC平行于AB之后，CD加上 DG再加上GL的和，可以等于 AB加上AL；或更确切地讲，从两边减去给定的GL，CD加上 DG必定等于一个给定长度。与前面的作图相比这已是一个较为简单的问题。这样找到的D点将是曲线应该通过的那些点之一。证明将与前面的相同。据此，也可以证明，来自L点的光波在穿过玻璃KAKB之后，将呈直线形，如BC；也就是说，光线将变得平行。由此反过来可以得到，照射在表面KDB上的平行光将汇聚于L点。

如图52，再假定有一给定的表面AK，它有绕AB轴旋转而得到的任何所需要的形状。假定中部的玻璃厚度为AB，又假定点L是玻璃后方的轴上的给出的一个点；同时假定照在表面AK上的光线是朝向这个点的。我们需要的是求一个表面BD，它能使从玻璃中出来的光线，看起来似乎是玻璃前方的点F出来的。

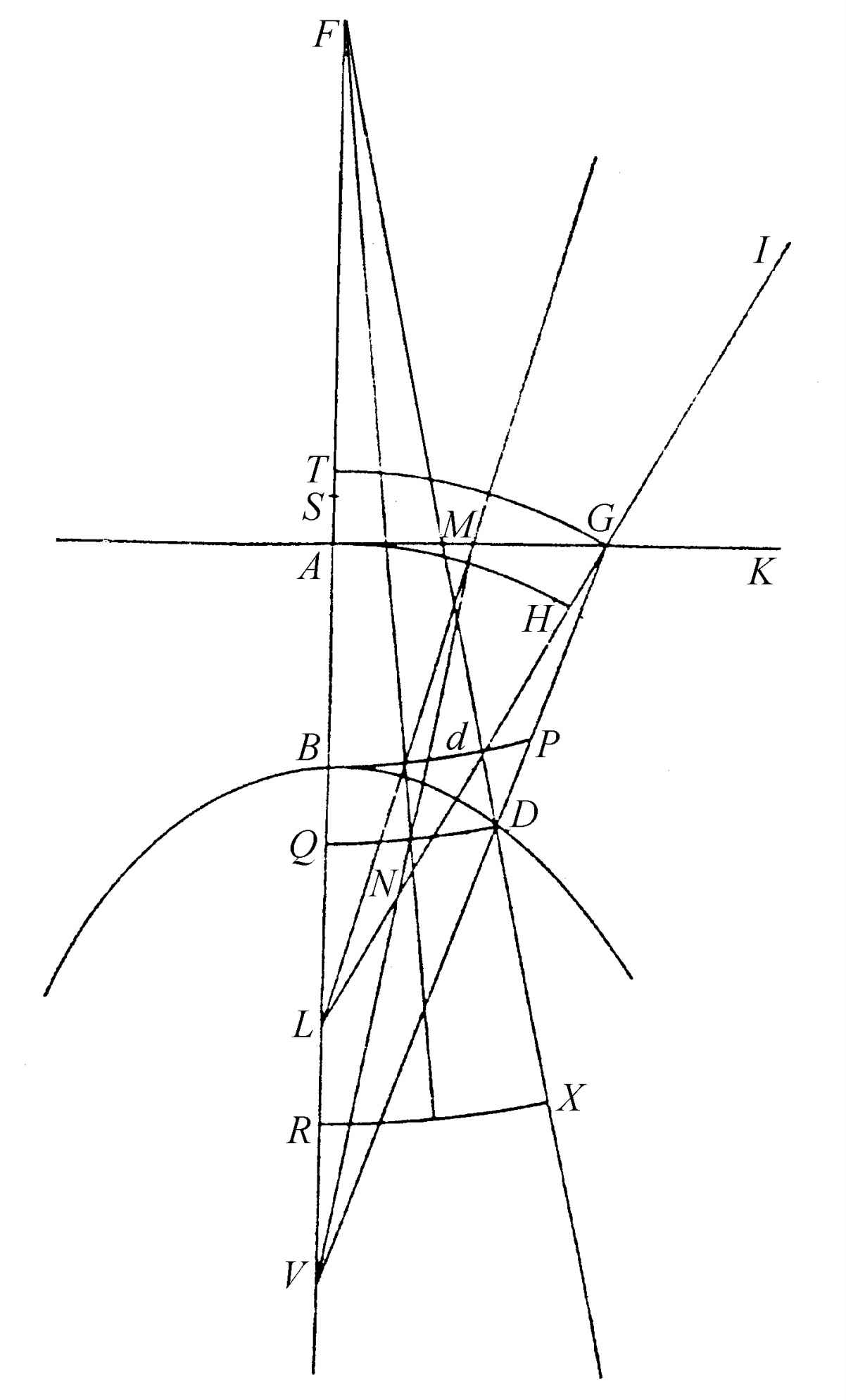图52

在线AK上取任意一点G，然后作直线IGL，它的GI部分将表示入射的一束光线，其折射线GV就可以求出。必须在这条折射线上找到点D，曲线DB应该通过它。假定点D已经找到：在距离LG大于LA时，以L为中心作圆弧GT，与直线AB相交于T。不然的话，必须以同一中心画弧AH，与直线LG相交于H点。这段圆弧GT（或者另外一种情况下的AH）将表示一束入射的光波，它的光线朝向点L。同样，以F点为中心作圆弧DQ，表示一束由F点发源的光波。

于是，光波TG在穿过玻璃以后，必然形成波QD。由此我观察到，光在玻璃中沿GD传播所需要的时间，必定等于它沿TA、AB以及BQ三段所需要的时间，其中仅有AB段在玻璃中。或者更确切地说，作AS等于 AT之后，我注意到， GD应该等于 SB加上BQ。把它们从FD或FQ中减去之后。FD减去 GD应该等于FB减去 SB。最后的这个差，是一个给定长度。我们所需要做的所有事情，就是从给定点F作与VG相交的直线FD，使得它满足以上所述。这是一个与用于这些作图方法中的第一个问题十分类似的一个问题。在那个问题中，FD加上 GD应等于一个给定的长度。

在证明中，必须注意，由于弧BC落在玻璃内，所以必须设想一个与之同心的并位于QD另一边的弧RX。那么，证明了光波GT上的G段到达D点的同时，T段到达Q点，就很容易作图得出，当Q段到达R点时，在D点产生的分波将与弧RX相切。于是这一圆弧应同时包括来自波TG的光运动；在这里所有其他的光波都被包括在内。

揭示了寻找这些用于完全汇聚光线的曲线的方法之后，剩下的就是要解释一件值得注意的情形，即有关球面、平面或者其他表面的不同等折射，如果忽略了这种情形，就会使人们怀疑我们先前重申过几次的观点，即光线与沿着与光波垂直的直线传播。

在某一情形下，例如，如图53所示，光线平行照射在球面AFE上面折射后彼此相交于不同点。在透明体中，与聚焦光线正交的光波会是什么样子呢？它们不会是球面的。当所说的这些光线开始彼此相交时，光波又会变成什么样子呢？通过对这一困难的解决，我们将看到产生了一些值得注意的东西，尽管光波不会继续完整，但也决不会中断，正如它们穿过依据要求设计的玻璃时我们所看到的那样。

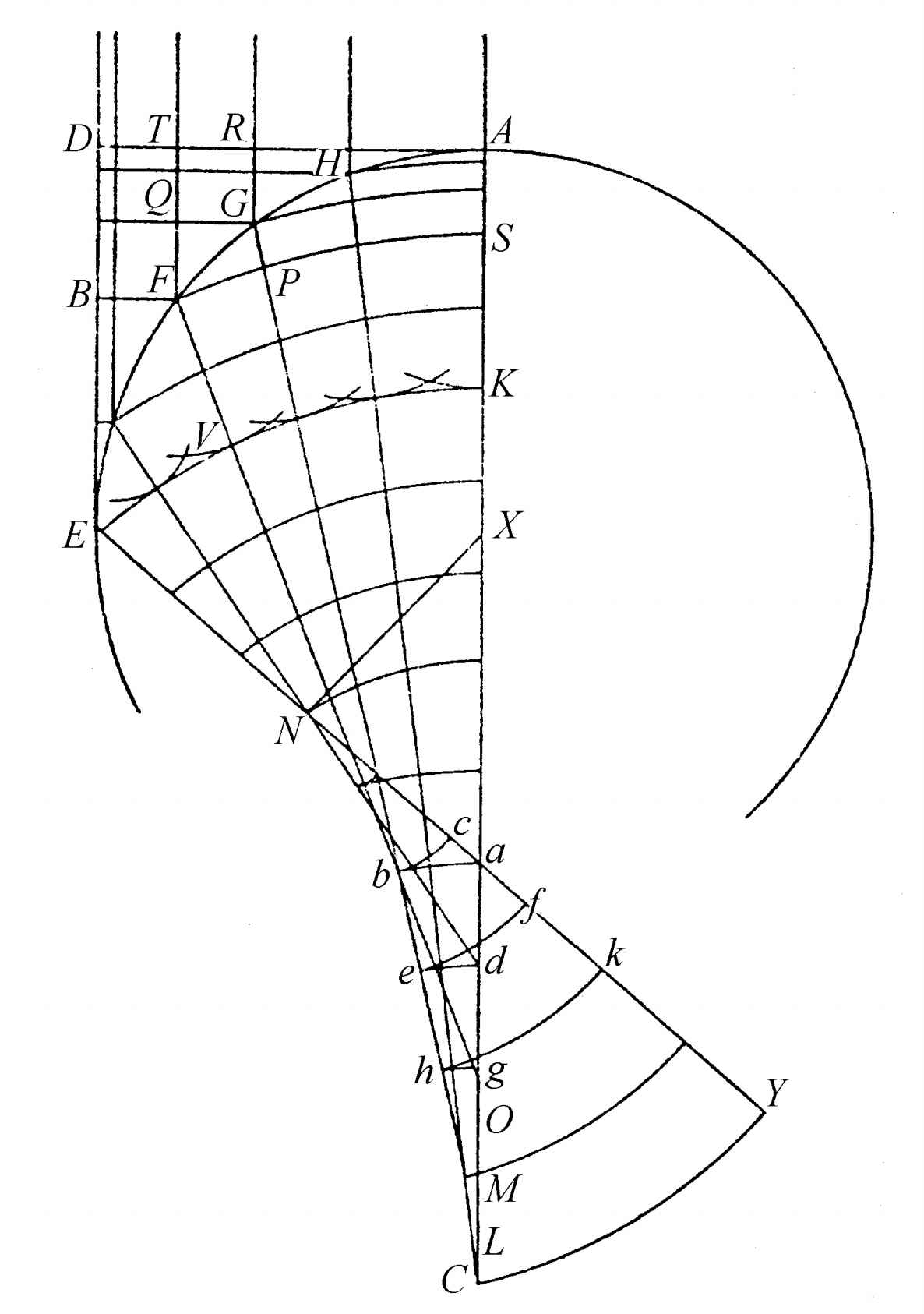图53

依据上面的证明，从球面顶点所作的与平行于入射光线的轴正交的直线AD，表示光波。当光波的D段到达球形表面AGE上的E点时，它的其他部分将也到达同一表面上的F、G、H等点，并以这些点为中心形成球面部分波。与所有这些分波相切的表面EK，为光从D段到达E点的时间内波AD的继续传播。如果我们设想在凸形曲线ENC上放有一条松开的细线，它的末端E构成了曲线EK，那么线EK不是一段圆弧，而是另一条曲线ENC的渐屈线。ENC同所有平行的光线的反射线HL、GM、FO等相切。假定了这种曲线是这样作成的，我们将证明由中心点F、G、H等形成的光波都与它相切。

曲线EK以及其他由曲线ENC以不同长度的细线作出的渐进展开曲线与所有的光线HL、GM、FO等正交，使得这些光线在两条这种曲线之间所夹的部分都相等。这一点取自于我们的《摆钟论》（de Motu Pendulorum）中的证明。假定入射光线互相之间距离十分接近，如果我们考虑其中的两束，RG与TF，作GQ垂直于RG。如果我们再假定与GM在P点相交的曲线FS，是由从F点开始的曲线NC的渐进展开，其中这一点F也即线FS所延伸到的地方。我们可能假设小段FP是一条垂直于光线GM的直线，同样，假设弧GF是一条直线。而GM是光线RG的折射线，并且FP又与它垂直，正如以上解释笛卡儿的发现时所证实的那样，QF与GP之比必定为3比2，即折射比。对于其他所有小弧GH、HA等，情况也类似。也就是说，在包围它们的那些四边形中，与轴平行的边与其对边之比等于3比2。于是，其中一组之和与另一组之和的比，也等于3比2。换句话说，假定V为曲线EK与光线FO的交点，TF与AS之比，DE与AK之比，以及BE与SK或者DV之比，都等于3比2。而作直线FB垂直于DE，BE与光在透明体外传播从F点发出的球面波的半径之比也为3比2。显而易见，在V点，光线FM与光波相交，与曲线EK正交。因此，光波同曲线EK相切。用同样的方法可以证明，对于以上提到的所有由点G、H等产生的那些光波，情况也是如此。在波ED上的D段到达E点时，它们到达曲线EK。

现在开始讨论在光线彼此交叉之后，光波会变成什么样子。结论是，它们将由此扭弯，并由两个邻接的部分组成，其中一部分是曲线ENC在一个方向上的一条渐屈线，而另外一部分是同一条曲线在相反方向上的一条渐屈线。于是，波KE向聚焦位置前进时变成abc，其中ab由c端固定的曲线ENC上bc的渐屈线形成，bc由E端固定的bE的渐屈线形成。同一光波随后变成为def，再变成为ghk，并最终变成为Cy。并由此光波的传播不再扭弯，而总是沿着曲线ENC的渐屈线行进，递变为末端在C的某条直线。

在这条曲线上甚至有一个部分EN是笔直的，其中N是从球面中心x所作的垂直于光线DE的折射线上的垂足。这里假定折射线与球面相切。光波的扭弯从N点开始，一直到曲线c的末端。它通过取AC比Cx等于折射比3比2，可以作出。

曲线NC上可能需要的其他一些点，可以利用巴罗（Barrow）先生在他的《光学讲义》（Lectiones Opticoe）一书的第12节中为别的目的而证明的一个定理来求得。值得注意的是，需要找出与这条曲线长度相等的一条直线。因为它与线NE之和等于已知的线CK。由于DE与AL之比等于折射比，所以从CK中减去EN后，余下的部分就等于曲线NC。

同样，在凹球面镜反射中扭弯的波也可以求得。如图54，假定ABC是过轴线的一个内凹半球面的某一截面，半球面的中心为D，它的轴DB平行于入射光。所有这些照在四分之一圆周AB上的光线的反射线，都将与端点E是半球面焦点的曲线AFE相切，换句话说，该点将半径BD分为两个相等部分。该曲线应当通过的这些点可以通过下述方法找到。过A点作某一弧AO，并作长度为其2倍的另一弧OP。再在F点把弦OP分割，使得FP部分为FO部分的3倍。那么，F即为所求的一个点。

图54

因为平行光线仅仅是照在凹形表面上的平行于AD的光波的垂线，当它们顺次地传播到表面AB时，它们通过反射形成了扭弯的光波。这种光波由两条曲线组成，它们是曲线AFE在两个相反方向的渐屈线。因而，取AD为入射波，当AG部分到达表面AI时，即当G段到达I点时，曲线HF与FI一起构成了波AG部分的传播，其中曲线HF与FI分别是从F点出发的曲线FA、FE的渐屈线。此后不久，当AK部分到达表面AM时，K段到达M点，曲线LN与NM将一起构成这个部分的波的传播。这种扭弯的光波将这样继续传播下去，直至N点到达焦点E。用凹面镜对着太阳，可以在烟雾或者扬尘中看到曲线AFE。应当知道，即当一个圆EB在另一个以D为中心以ED为半径的圆中滚动时，不是别的，而唯有这一条曲线是E点在圆EB的圆周上画出的曲线。因而它是一种摆线，可以通过几何方法来求那些点。

与前面曲线的测定方法极为类似，利用这些波可以证明和求出，它的长度正好等于球面直径的 。虽然也可以使用其他一些方法，我从选题中略去了它们。由 圆弧，直线BE和曲线EFA所围成的面积AOBEFA，等于扇形DAB面积的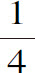 。