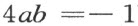附录Ⅴ　常高斯曲率曲面 ^（1）

负常曲率曲面

按照贝尔特拉米（Beltrami） ^（2） 的意图，如果取负常曲率曲面的测地线作为罗巴切夫斯基平面（非欧平面）的直线，且将曲面上实际的长度和角度作为罗氏平面内的长度和角度，则这个负常曲率曲面就可以理解为罗氏平面的一部分。在负常曲率曲面的研究中至今还没有发现在每一点的邻域内由于切面连续变化而曲面却能到处连续伸展。甚至在人们所熟知的具有奇异曲线的负常曲率曲面中，当其切面连续变化时，曲面却能连续伸展也是不可能的。由于这个原因，没有人能借助一个熟知的负常曲率曲面，而将其理解为完整的全部罗氏平面。这就引出一个具有原则性的有趣问题，按照贝尔特拉米的思想方法，是否整个罗氏平面能用一个负常曲率解析 ^（3） 曲面来表示。

为了回答这个问题，我们将从具有负常曲率为-1的曲面开始。假定这个曲面在有限区域处处正则且没有奇异点。我们证明这个假定将引出矛盾。对这样假定的一个曲面，我们可以用下述论断完全地刻画出来：

位于曲面的有限区域内曲面上点的每个极限点也是这曲面的点 ^（4） 。

设O 是曲面上任一点，则总能以O 为原点建立直角坐标系，且在原点邻近，曲面方程可以写作

其中a ，b 是常数且适合关系

^（5）

又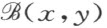 为x ，y 的幂级数，它仅包含x ，y 的三次幂和高次幂。显见z 轴是沿曲面的法线，而x 轴及y 轴的方向则是由曲面的主曲率所决定。

方程

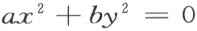
确定XY 面上过点O 的曲面的两条主切线 ^（6） 。由此可见这两切线永远不相重，且它们给出曲面上所取任意点O 的两条渐近曲线的方向。这两条渐近曲线中的每一条都属于某一个单参渐近曲线族，且它们规律地覆盖着O 点的整个邻域而没有任何空隙。取两个足够小的数值u 及v 而完成下面的作图：沿过点O 的两条渐近曲线之一截取长度等于参数u 的值而得到一个端点，再作过此端点的另一条渐近曲线，并截取其长等长参数v 之值的一端点，则这个端点将是曲面上由参数u 和v 唯一确定的一点。设曲面上一点的直角坐标x ，y ，z作为u ，v 的函数，即

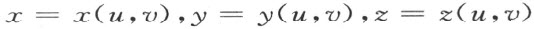
则就u ，v 足够小的值，它们是u ，v 的正则解析函数。

由熟知的常曲率为﹣1的曲面理论，可进一步得到下面的结果：

如果φ 是过点（u ，v ）的两条渐近曲线的夹角，则可得曲面的三个第一类基本量的值为

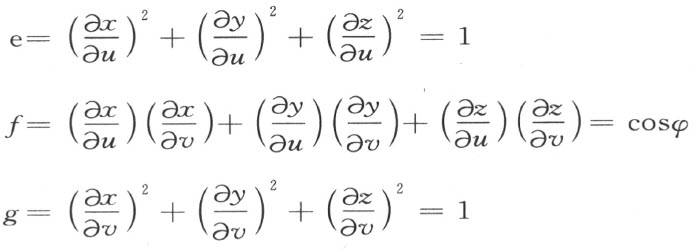
因此，这曲面上任意一条曲线的弧长关于参数t 的导数的平方将由下面的形式得出：

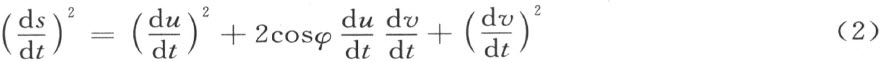
将角φ 作为u ，v 的函数，则它适合偏微分方程

^（7）

如果去掉数对u ，v 与曲面上点之间的一一对应的要求，则我们可就任一对u ，ν 值来说明上面的作图。的确，过O 点所作的u 曲线甚至可能是封闭的。但不论哪种情况，前面有关曲面的假设，沿过O 点的u 曲线的两侧均可截取任意大的长度u 。这样关于每一个u 值，对应着渐近曲线上的一点。

今考虑经过这样的每一个点P 作另一条渐近曲线。在这曲线上，自P 点（沿一个方向）取长度为参数v 的一段，再者，沿这条渐近曲线，于P 之两侧取足够大的长度也是可能的。

这样，每对u ，v 之值就唯一地对应着曲面上某一点，然而一般说来不能是唯一且是可逆的。用几何语言来说就是：我们将得到由整个欧几里得（u ，v ）的平面到已知曲面的某覆盖（重叠）曲面或者它的一部分的一个映射。

现在的问题是要证明曲面上每一条u 曲线是渐近曲线，且参数u 是它的弧长。对于曲线v ＝0的情况这是已经知道的。再者由（2）所表示的弧元素，对点（u ，0）邻域的v 曲线的弧长也是成立的。

关于一般情况，仅证明下列论断就够了。

设a 是一个正数，b 是任一实数，则每个线段

在曲面上的象是一条渐近曲线的一个弧段，或者是沿这样一条曲线上弧段的并且u 表示它的长度。

其次这个命题于b ＝0时成立，而且可以证明：

1．如果这个命题于b ＝b ₀ 时成立，则对不同于b ₀ 而与b ₀ 充分接近的每一b 值也将成立。

2．如果这个命题于b ₁ <b <b ₂ 时成立，则于b ＝b ₁ 及b ＝b ₂ 时也成立。

这些可以经过连续性论证及利用海因内-波雷尔（Heine-Borel）有限覆盖定理的一个应用来证明。

于是这个命题就b 的所有值得以证明。

如果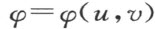 表示过曲面上点（u ，v ）的两条渐近曲线的交角，这个角系由正u 方向到正v 方向来度量的。于是φ （u ，v ）是对（u ，v ）的所有值规定的连续函数。这个函数具有适合微分方程（3）的连续偏导数。

适当选取正u 方向和正v 方向即可推出不等式

于点u ＝v ＝0处成立。

因为φ 无处等于0或π，于是由φ （u ，v ）的连续性，

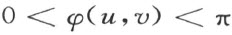
这样就u ，v 所有值

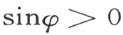
然而具有这些性质的函数φ （u ，v ）是不能存在的。

自微分方程

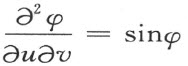
可得

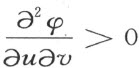
于是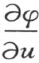 随v 值增加而增加。

特别地，

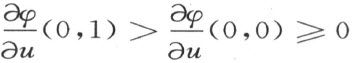
因之可以确定一个正数a 使得a ≤u ≤3a 时，

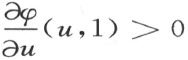
设m 表示

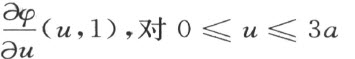
的正极小值。

于是就v≥ 1：

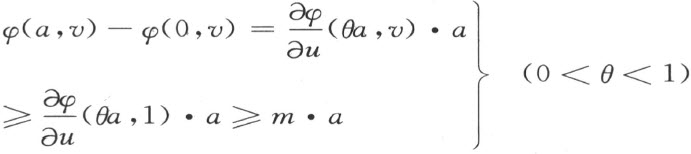
同时也有

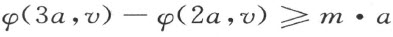
因之

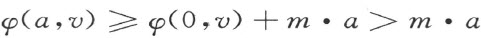
且有

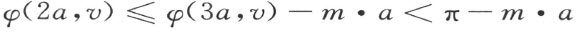
再者就 ：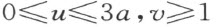

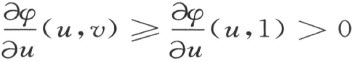
因之φ （u ，v ）随u 单调增加，故对

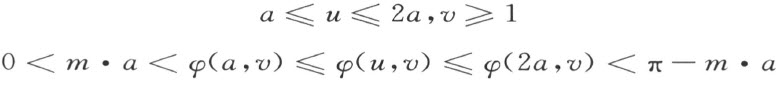
而得

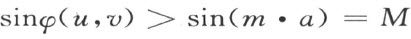
这里M >0且与u ，v 无关。

于是展布在以

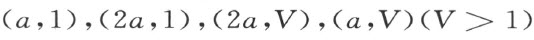
为顶的矩形上的二重积分

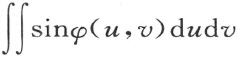
的数值将大于

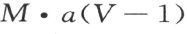
当适当选取V 时，可使其大于π。

另一方面，从微分方程（3）可以得出

这是由于

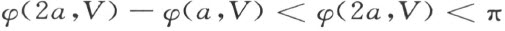
以及

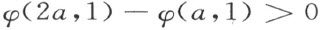
的缘故。

因此得到一个矛盾。这样开始所给的基本假设应被推翻。亦即，可以看出，不存在非奇且处处正则具有负常曲率的解析曲面。特别地在开始时所提的问题，按照贝尔特拉米的想法，是否整个罗巴切夫斯基平面能被理解为空间的一个正则解析曲面，这个问题的回答是不可能的。

正常曲率曲面 ^（8）

在开始研究这个问题之前，我们回顾对处处正则且在有限区域内解析的负常曲率的曲面，结果是这样的曲面并不存在。现在借助于相应的方法来研究关于正常曲率曲面的同样问题。显然，球面是封闭的且不具备奇异性的正常曲率曲面，并且在我的激励下，李勃曼 ^（9） （H.Liebmann）所给出的证明推出不存在其他具有同样性质的闭曲面，这个结果可以归纳成下面的一个定理，它对于无奇异性的正常曲率曲面 ^（10） 的任何部分都是适合的。

在正常曲率为＋1的曲面上，如果规定一个有限的、不具有任何奇异性的单连通或多连通区域，在此区域的每个内点连同其界点作曲面的两个主曲率半径。假如曲面是单位球面的一部分，则于这个区域内部中的点达不到这两个主曲率半径较大者的极大值，因之也达不到较小者的极小值。

为了证明，首先由假设，两个主曲率半径之积处处等于1，因之两个主曲率半径之大者必须大于或等于1，假如曲面块上每点的两个主曲率半径均为1，则较大的主曲率半径显然为1。在这种特别情况下，曲面块的每一点均是脐点，我们可以用熟知的方法断定曲面块必是单位球面的一部分。

其次假设曲面的两个主曲率半径的极大值大于1。假定前面所说结论不成立，则在曲面块内部存在一点O 在此点具极大值。由于这个点不能是脐点，而是曲面的一个正则点，因之在这点邻近被两个曲率线族的每一个所覆盖而无空隙。取这两族曲线为坐标曲线且以O 为原点，则根据熟知的正常曲率曲面理论得到下面事实 ^（11） ：

设r ₁ 表示在原点O ＝（0，0）的邻域，内点（u ，v ）处两主曲率半径中之较大者，在这个邻域中r ₁ >1。并设

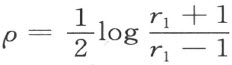
作为（u ，v ）的函数的正实数ρ 适合偏微分方程

因为ρ 必须随r ₁ ，递减而递增，于是ρ 作为u ，v 的函数必须于u ＝0，v ＝0处得到一个极小值。因此ρ 依变数u ，v 的幂展开必有以下形式：

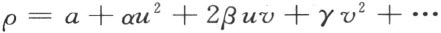
这里a ，α ，β ，γ 都是常数，并且二次形式

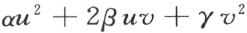
就u ，v 的实值永不能假设为负。由最后条件常数α 和γ 必有不等式

另一方面，将ρ 之展式代入微分方程（4），由于u ＝0，v ＝0，我们得出

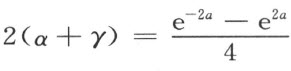
既然常数a 表示ρ 在点O ＝（0，0）处的值，且其值必须为正，上式右端在任何情况下必小于0，于是可得不等式

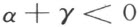
此与方程（5）相矛盾。因此由原假设，即在曲面块内部一点得到极大值是不可能的。故上面所列出的定理得以证明。

再者，由上所述可立即得出定理：无奇异性且具有正常曲率为1的闭曲面必是单位球面。 这个结果同时说明下述事实：在球面上某处没有奇异性，不能将球面作为整体来弯曲。

最后，自上面所论引出非封闭曲面的以下结果：若从球面上割掉一部分，并任意弯曲，则所有主曲率半径之极大值总在曲面这部分的边界上出现。

1900，格丁根。

关于这个附录的近代发展就是整体微分几何的一部分内容，可参看下列著作：

1．本文第一部分近代常称为希尔伯特定理，它的叙述是：在三维欧几里得空间内不存在常负曲率的完全曲面。

可参看

J．J．Stoker，Differential Geometry，1969，265—271。

M．P．do Carmo，Differential Geometry of Curves and surfaces，1976．446—453。

2．本文第二部分的最初文献见：

李勃曼“球面的一个新性质”（Eine Neue Eigenschaft der kugel，Nach．Kgl．Ges．Wiss.，Göttingen，Math．Phys.，Klasse，44—55）。

近代常称为李勃曼定理，它的叙述是：设S 是紧致、连通、常曲率为K （>0）的曲面，则S 必是以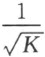 为半径的球面。可参看：

Chuan-chih Hsiung（熊全治），Differential Geometry，1981，247—249

3．尼伦贝格（L．Nirenberg），Seminar on Differential Geometry in the Large，1956。

4．希尔伯特定理中“常曲率条件”是非本质的。1963年莫斯科大学一些数学家曾证明：在三维欧几里得空间，完全正则曲面中高斯曲率的上确界是非负的。——译者注

荷兰画家霍贝玛（Meindert Hobbema，1638—1709）的《米德尔哈尼斯的林荫道》（Avenue at middelharnis ）。画中在舒缓的水平线上又叠加了垂直，一种极具几何美的透视缩减给空间注入了三维空间感。

1900年希尔伯特在巴黎第二界国际数学家代表大会上提出了23个数学问题（史称希尔伯特问题），激发了整个数学界的想象力。此后，这些问题几乎成为检阅数学重大成就的指标。希尔伯特去世时，德国《自然》杂志发表过这样的观点：现在世界上难得有一位数学家的工作不是以某种途径导源于希尔伯特的工作。他像是数学世界的亚历山大，在整个数学版图上，留下了他那显赫的名字。

1900年巴黎数学家大会报告的封面。

希尔伯特在巴黎数学家大会上提交的报告的篇头。

希尔伯特问题中著名的第十个问题的笔记，这条笔记大约写于1886年，大大早于希尔伯特23个问题发表的1900年。

就希尔伯特的第十个问题在2007年召开的研讨会的海报。

欧几里得《几何原本》中的一页。

明刻本《几何原本》书影。

欧几里得《几何原本》较早的英译本封面。

《几何基础》德文版封面（左）和第10次印刷的《几何基础》英文版封面（右）。《几何基础》的第一版于1899年出版，后经多次修改，目前一般引用1930年出版的第七版。希尔伯特在书中对欧几里得几何及有关几何的公理系统进行了深入的研究。他不仅对欧几里得几何提供了完善的公理体系，还给出证明一个公理对别的公理的独立性以及一个公理体系确实为完备的普遍原则。希尔伯特的《几何基础》把几何学引进了一个更抽象的公理化系统，重新定义了几何，不但改良了传统的欧几里得的《儿何原本》，更使几何学从一种具体的特定模型上升为抽象的普遍理论。

1916年的德国《物理学年鉴》封面及《广义相对论基础》首页。

1915年，爱因斯坦（Albert Einstein，1879—1955）在格丁根作了一次关于广义相对论的讲演，在这里他结识了希尔伯特，两个人很快就成为非常要好的朋友。10月底，爱因斯坦几乎停止了与所有人（贝索、洛伦兹等人）的通信，只与希尔伯特保持联系。在此之前，爱因斯坦对广义相对论的探索，因为数学上的困难，仍然停留在1913年的雏形阶段，几乎没有任何可以称道的进展。在这关键的11月，正是由于与希尔伯特的多次信件交流，在经历了8年的沉寂之后（从1907年起），广义相对论的最终形式终于浮出水面了。1915年11月25日，爱因斯坦向柏林的普鲁士科学院递交了题为《引力的场方程》的论文，提出了广义相对论引力论的完整形式，最终完成了广义相对论的逻辑构造。

希尔伯特曾经幽默地评价爱因斯坦的相对论，他说：“我们这一代人一直在探讨关于时间和空间的问题，而爱因斯坦说出了其中最具独创性、最深刻的东西。你们可知道这里的原因吗？那就是因为，有关时间和空间的全部哲学和数学，爱因斯坦都没有学过。”

冯·诺依曼（John von Neumann，1903—1957）年轻时是希尔伯特家的常客，他对希尔伯特的物理学和证明论思想有浓厚的兴趣。这两位年龄相差40多岁的科学家，在希尔伯特家的花园或书房里一起度过了许多难忘的时光。1933年，冯·诺依曼解决了希尔伯特第五个问题。

玻恩（Max Born，1882—1970），德国理论物理学家，量子力学的奠基人之一，1954年荣获诺贝尔物理学奖。1905年前后玻恩到格丁根大学听希尔伯特、闵可夫斯基等讲学，并成为希尔伯特的“私人”助理，这为他后来在量子力学获得的巨大成就奠定了坚实的数学基础。

海森伯（Werner Karl Heisenherg，1907—1976），量子力学的奠基人之一，1932年荣获诺贝尔物理学奖。海森伯评价说：“希尔伯特对格丁根量子力学发展的影响最为巨大，凡是20年代在格丁根学习过的人，对于这种影响都有充分体会。”希尔伯特和他的同事们创造了一种特有的数学环境，所有年轻的数学家都是按希尔伯特积分方程和线形代数理论所体现的思想训练出来的，因此，对于这些领域中的每一项理论发展来说，格丁根始终是比其他任何地方更合适的场所。现已表明，量子力学的数学方法原来是希尔伯特积分方程理论的直接应用，这确是一件特别幸运的事情。

这条大约写于1888年的笔记显示希尔伯特在康德哲学基础上思考数学科学的基石。

德国数学家给springer出版社发出的联名信，感谢该出版社在二战后出版的一系列有关数学物理的优秀读物，签名的第一、第二位分别是克莱因和希尔伯特。

希尔伯特的《几何基础》手记的第32～33页。

希尔伯特的漫画像。

邮票上的希尔伯特。

格丁根大学教室里的希尔伯特画像。

希尔伯特经常下午在格丁根的这条小道上散步。

位于格丁根的以“大卫·希尔伯特”命名的街道。

伦敦数学学会大楼。1901年希尔伯特被授予该学会荣誉会员。

由于思想的深刻性、方法的创造性以及证明的严密逻辑性，希尔伯特对数学的发展作出了巨大贡献。1910年匈牙利科学院（图）授予希尔伯特第二次鲍耶奖。该奖是为了纪念非欧几何的创始人之一匈牙利数学家鲍耶（John Bolyai, 1802—1860）设立的。该奖第一次得主是庞加莱（Jules Henri Poincaré, 1854—1912）。

伦敦皇家学会大楼。1928年希尔伯特成为伦敦皇家学会会员。

————————————————————

（1） 希尔伯特“论常高斯曲率曲面”（Über Fläche Von Konstanter Gauβcher Krümmung）一文曾发表在美国的数学杂志Trans．AMS．Vol．2，1901上，以后转载于第七版以前的《几何基础》书内而作为附录Ⅴ，从第七版起由希尔伯特本人重新改写，去掉原发表杂志的名称，直到第十二版未曾变动。——译者注

（2） Giornale di Matematiche，Bd．6，1868。

（3） 为了简单的叙述，这里假设所考虑的曲面具有解析性，虽然就其论述以及所得结果，当方程（1）中的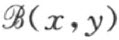 是x ，y 充分可微的非解析函数时仍能成立。吕特开美尔（G. Lütkemeyer）在我的激励下在他的就职论文报告“论偏微分方程的积分的解析特性”（Über den analytiscnen Charakter der Integrale von partielle Differential-gleichungen，Göttingen，1902）中曾经证明了确实存在曲面理论意义下非解析的负常曲率曲面（按照后面证明的定理没有一个处处具有连续变化的切面而却能连续伸展的曲面）。

（4） 利用现代数学语言就是说这个曲面是完备曲面。即曲面上每一个哥西点叙列仍收敛于这个曲面上一点。——译者注

（5） 经过计算，曲面于O 点处高斯曲率是＋4ab 即﹣1。——译者注

（6） 它们是原点处杜班（Dupin）标线的渐近线，因此俄译本译作渐近切线。——译者注

（7） 以这些公式为基础，我首先证明不具有奇异性的负常曲率曲面不可能存在（Trans．AMS，Vol.2，1901）。其后赫尔姆格兰（E. Holmgren）也以公式（3）为基础给出一个更广泛的解析证明（Comptes rendus，巴黎，1902）。本文引进修改了的Holmgren的证明与W．Blaschke在他的微分几何中［Vorlesungen üleer Differentialgeometrie，I，section 80（1921）］所介绍的相符合。同我的原始证明一道也接近于L．Bieberbach，Acta．Mathematica，Vol.48。

（8） 关于非欧椭圆平面几何利用处处连续的弯曲曲面表示的问题的研究，鲍埃（W. Boy）在我的鼓励下作了“关于全曲率以及闭曲面的拓扑学”（Über die Curvatura integra und die Topologie geschlossener Flächen，Göttingen，1901以及Math．Ann．Bd．57，1903）的就职论文报告。在那里，鲍埃拓扑地设计了一个很有趣的有限曲面。这曲面在一侧是封闭的，除去自交成一个具有三重点的封闭二重曲线外，它没有奇异性；并且具有与非欧椭圆平面相同的连通性。

（9） 见Göttinger Nachrichten（1899，44页），也请参看原作者在Math．Ann．卷53与卷54上的有趣工作。

（10） 吕特开美尔的就职论文报告以及赫尔姆格兰在Math．Ann．卷57的文章都证明了正常曲率曲面的解析特征。

（11） 达尔布（Darboux）《曲面一般理论讲义》（Leçns sur la théorie génerale des surfaces，Bd，3，Nr．776），比安契（Bianchi）《微分几何讲义》（Lezioni di geometria diffenziale，§264）。