第4章　论空气的折射

显而易见，当物质不是均匀的，而是使运动在其中一边比另一边传播得更快的一种结构，光的波就不再是球面的：而需要随连续的运动在相同时间里通过的不同距离来确定它们的形状。

1688年惠更斯手绘的真空泵插图

我们已经说明了在任何均匀物质中构成光的运动是怎样通过球面波传播的。显而易见，当物质不是均匀的，而是使运动在其中一边比另一边传播得更快的一种结构，光的波就不再是球面的：而需要随连续的运动在相同时间里通过的不同距离来确定它们的形状。

因此，我们将首先解释空气中发生的折射，从这里到云层和云层之外。这种折射效应很值得一提，因为通过它们我们常常能看到一些本来已被地球的球体所遮蔽的东西，譬如岛屿以及人们在海上看到的山顶。也正是因为这种效应，太阳和月亮看起来在它们真正升起之前就已经升起来了，而落下去时又似乎迟一些：以至于经常看到月食出现时太阳仍然地平线上。同样，如天文学家所知道的，也是由于这种折射效应，太阳和月亮的高度以及所有星星的高度看起来总是比实际上高一些。不过有一个实验更明显地表现了这种折射效应。实验是在某个位置上固定一个望远镜，使之能观察到半里格或更远距离外的物体，譬如一座尖塔或一栋房子。那么，如果你在一天的不同时间中来观察，并以同一种样子固定望远镜，你就会发现物体上的同一点并不总是出现在望远镜筒孔的中部，而通常在早晨和傍晚当地面上有较多水汽时，这些物体好像升高了一些，以至于有一半或一半以上看不到了；而到正中午当水汽消散时它们显得较低。

那些以为折射现象只在性质不同的透明体的隔离表面上发生的人应当发现，很难对我刚才提到的那些现象给出一个解释。但是根据我们的理论，这件事却是十分容易的。众所周知，我们周围的空气，除了漂浮在曾交代过的“以太”物质中的自身微粒以外，还充满了因热作用蒸发的水微粒。一些十分明确的实验进一步地证实，如果人们登得更高一些的话，空气的密度将成比例地减小。无论水和空气微粒是否凭借“以太”微粒参与构成光的运动，反弹都不如“以太”微粒迅速，即无论这些空气和水的微粒对于“以太”过程的运动传播造成的对抗与阻碍是否迟滞了“以太”过程，都可以得出，在“以太”微粒中飞来飞去的这两种微粒必定使空气从相当高的地方到地面逐渐变得不容易传播光波。

图13

由此，波的形状应该变得接近于图13所示：即，如果A是一盏灯或者是一座尖塔上的可见点，那么它发出的波应该向上传播得宽广些，向下不太宽广，而在其他方向则或多或少地接近于两端。由此必然得出，除了与地平线垂直的那一条直线以外，所有与波正交的线都从A点的上方穿出。

设把光传到观察者B的波为BC，与波垂直相交的直线为BD。因为在我们看来我们借以判断物体方位的光线或者直线同到达我们眼睛的波的正交线没有什么两样，所以依照上述说法来理解，显然A将被感觉到是位于直线BD上，因而比实际要高。

同样，如图14，如果设地面为AB，大气层的顶部为CD，这里的CD可能不是一个轮廓分明的球面（因为我们知道随着人们登高，空气按比例变得稀薄，使得高处的空气的压力是如此之小），来自太阳的光波以这样一种方式，例如，它们在没有进入大气层CD前与直线AE正交，则当它们进入大气层后，在高空比在地面附近前进得更快。因此，如果CA是把光载至A点观察者的波，它的C区域将前进得最快；而与这个波正交的直线AF决定了太阳的视在位置，比沿AE看见的实际的太阳位置要高。由此可能产生以下现象，没有水蒸气时本来不应该被看到的太阳，由于直线AE碰着地面，通过折射在线AF上被看到。不过由于水汽稀薄只是些微地改变光波，所以角度EAF几乎不会超过半度。而且这些折射并非在所有天气下都是一致的，尤其是对于2度到3度的小仰角情形，这是由于自地面升起的水汽量的不同而引起的。

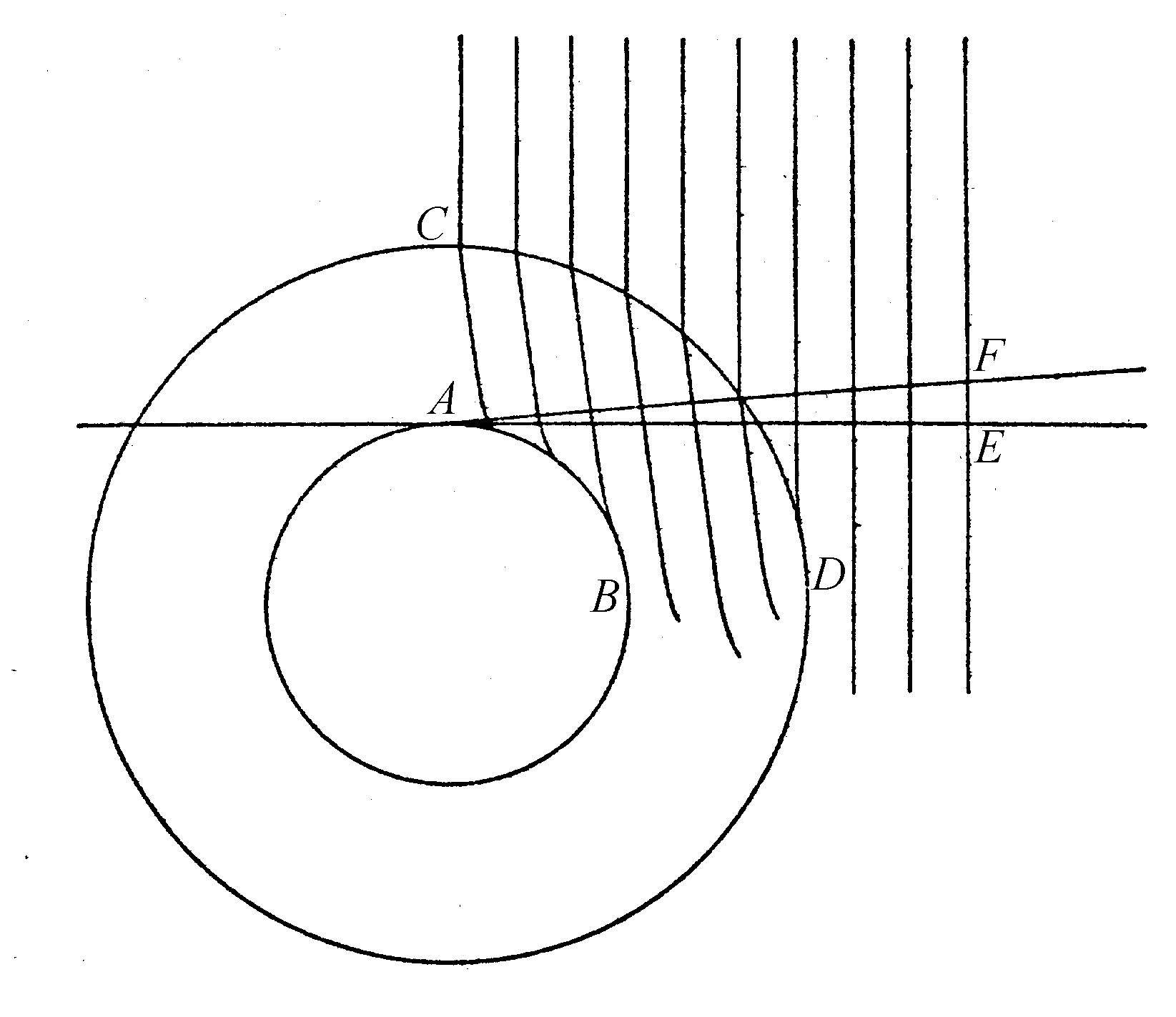图14

这也是为什么尽管在相同的地点观察，在某个时刻一个远距离的物体会被另一个稍近距离的物体遮蔽，而在另一个时刻它却可能被观察到。这个效应的原因在我们将要论及的关于光线的弯曲的内容中，会表现得更为明显。从上面的解释中似乎可以得出一个结论：光波的一小部分的行进或传播就是我们称之为光线的东西，在一个透明度不均匀的大气中，这些光线应该是弯曲的，不再像它们在均匀介质中那样笔直。因为正如我们将要证明的那样，光线必定像图13那样，沿着与所有波正交的线AEB，从物体传送到眼睛；而且也正是这条线决定了位于中间物体能否阻碍我们看到目标。尽管尖塔A点看起来似乎升到了D点，但由于塔H位于二者之间，它还是不会为眼睛B所观察到，因为H同曲线AEB相交了。而曲线下方的塔E，就不能阻碍人们观察到A点。现在，根据地面的空气密度比其上空的大这一事实，光线AEB的曲率将变大：以至于在某一时刻它将从顶点E的上方穿过，使得眼睛B能够观察到A点；而在另一时刻它却被同一塔E所截断，使得同样的眼睛看不见A点。

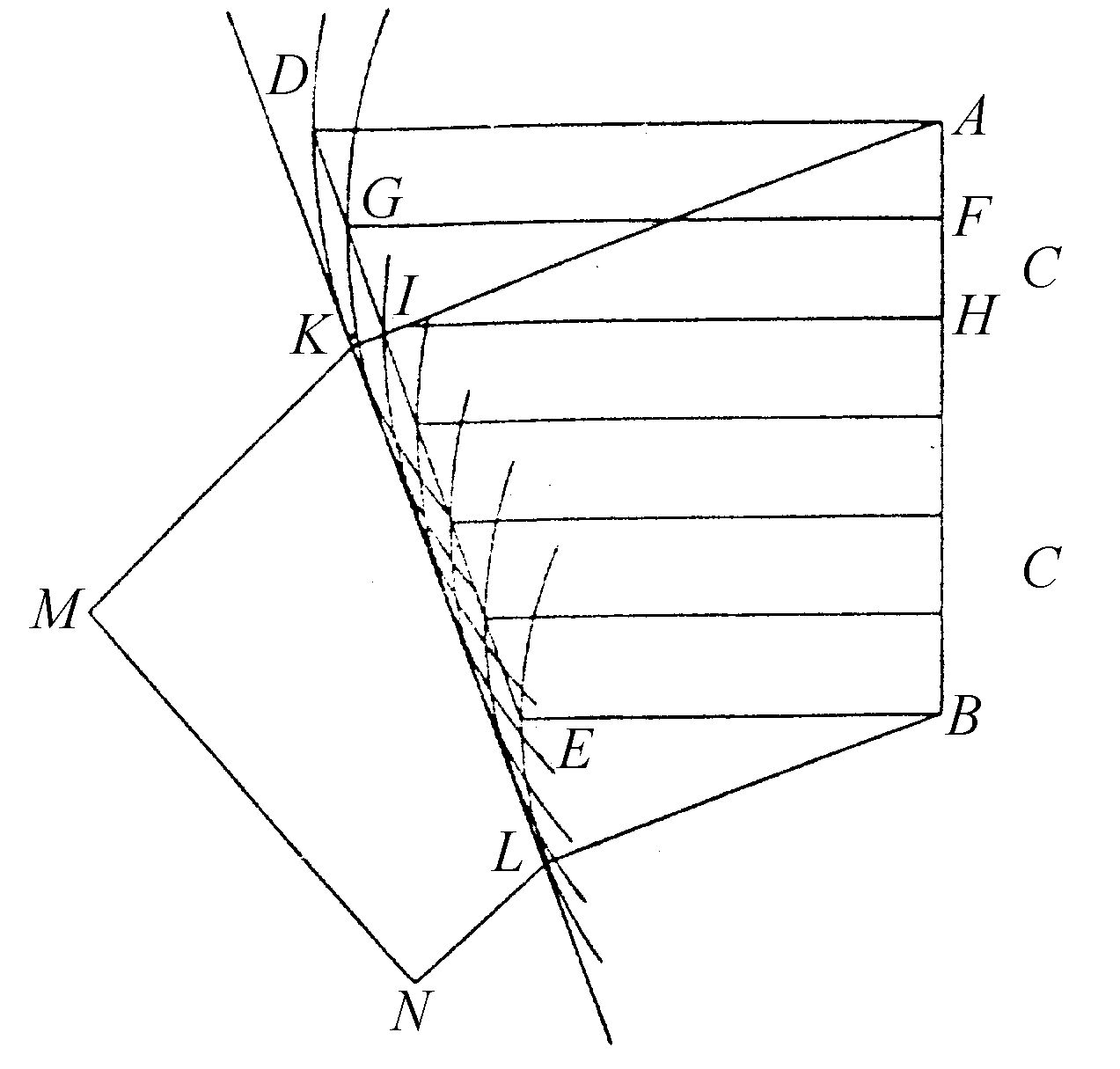图15

为了证明这种光线弯曲同我们前面所有的理论是一致的，我们假定AB为来自C方的光波的一个小部分，而这一光将被我们认为是直线（图15）。又假定AB同水平面垂直，B比A靠近地面。因为水蒸气在A点的阻尼比在B点小，来自B点的部分波传播过一个较短距离BE时，来自A点的分波传播过一个距离AD，而AD与BE都与水平面平行。另外，设FG、HI等直线由直线AB上的各点划向线DE（DE是直线或者可被认为是直线），并假定A与B之间不同高度上大气的不同透明度由这些线来表示；那么当来自A点的部分波传播过空间AD时，来自F点的部分波将传播过空间FG，来自H点的部分波将传播过空间HI。

如果以A和B为圆心，画出表示来自这两点的波传播的圆DK和EL，并作直线KL同这两个圆相切，很容易看出KL这一条直线将是所有以F、H等为圆心所画的其他圆的公切线，并且所有切点都将落在垂线AK和BL所夹的这个线段上。于是，线KL将包络来自AB上各点的分波的运动；并且在同一时刻，KL之间的运动将比在其他地方要强，因为无数个圆在一起构成了这条直线。因而KL将成为波AB部分的传播，正如我们在解释反射和正常折射时所说的那样。显而易见，AK与BL将向空气中不太透明的那个方向倾斜，因为AK比BL要长并与它平行，所以线AB与KL被延长后将在L那一边相交。而角K是直角，因此角KAB应为锐角，也就小于角DAB。如果用上述的同样方法来考察波KL部分的传播，就会发现再过一段时间后它将到达MN，并且垂线KM和LN比AK和BL更加倾斜。这足以证实，正如我们所说的那样，光线将沿与所有波正交的曲线传播下去。