第二章　论气量法，即气态物质的重量与体积之测量

第一节　论气体化学装置

近来法国化学家们已经把气体化学装置这一名称用于普里斯特利博士所发明的非常简单而精巧的机械装置，该装置现在是每一个实验所必不可少的。这由一个木槽组成，木槽尺寸依方便或大或小，镶有铅皮或镀锡铜皮，如图版V 透视图所描绘的那样。图1 中，同一个槽或池的两面假定被切走了，以更清晰地显示其内部构造。在这个装置中，我们分清隔板ABCD（图1和图2 ）和池底或池体FGHI（图2 ）。广口瓶或玻璃钟罩按此深度充满水，将其翻转，口朝下，然后竖立在隔板ABCD上，如图版X图1F 所示。隔板平面以上池边的上部称为边（rim ）或缘（borders ）。

池子应当充满水，以便在隔板之上至少保持一时半的深度，池子的尺寸至少应当使池子的每个方向都有一呎水。这种大小足以满足一般的需要；但有较大的空间常常较方便甚至有必要。因此，我建议打算有效地从事化学实验的人们把这种装置做成大尺寸，使他们有地方操作。我的主池能容四立方呎水，其隔板有十四平方呎的表面；虽然我起初认为这个尺寸太大，但现在我常常苦于缺乏空间。

在完成大量实验的实验室里，除了一个可以称为总池（general magazine ）的大池之外，还必须有几个较小的池子；甚至一些轻便的池子，必要时可将它们搬到炉子旁边或任何能够搬到的地方。也有一些操作把装置的水弄脏，因此这些操作需要在池子里独自进行。

使用简易楔形接合的木质池子或包了铁的桶，而不是镶了铅或铜的桶，无疑会相当廉价；在我最初的实验中，我用的是用这种方式做的池子；但是不久我就发现它们不方便。假若水不总是保持相同的高度，那么楔形榫就会干缩，而当再加水时，水就通过接榫处流出跑掉。

我们在这种装置中使用水晶瓶或玻璃钟罩（图版V，图9，A ）盛气体；当装满气体时为了将它们从一个池子移往另一个池子，或者当池子过挤时为了保存它们，我们用一个平盘BC，平盘由直立的边或缘围着，带有两柄D和E。

在用不同材料做了几个试验之后，我发现大理石是建造汞气体化学装置的最好物质，因为汞完全透不进它，而且它不像木头那样，易于在接榫处分离，让汞通过裂缝逸出；也不像玻璃、缸瓷或瓷类那样，冒破裂的危险。取一块大理石BCDE（图版V，图3和图4 ），约2呎长、15或18吋宽、10吋厚，像在mn 处（图5 ）那样将其挖空至少4吋深，作为储汞槽；为能较方便地填放广口瓶，凿一道至少约4吋深的沟TV（图3、4和5 ）；由于这道沟有时也许证明是麻烦的，可以将薄板插入槽xy （图5 ）之中，随意将其盖上。我有这种构造的两个不同尺寸的大理石池子，我总是可以用其中的一个作为储汞槽，它保存汞比其他任何容器都安全，既不易翻倒，又不易发生其他事故。我们用汞在这种装置中操作，恰恰如同前面描述的用水在这种装置中操作一样；不过玻璃钟罩必须有较小的直径并且坚固很多；我们也可以使用图7 中的阔口玻璃管；这些玻璃管被卖玻璃的人称做量气管（eudiometer ）。图5A 描绘的竖立在其位置上的一个玻璃钟罩，叫做广口瓶的东西制成了图6 。

在离析了的气体能被水吸收的一切实验中，汞气体化学试验装置都是必需的，除了金属化合物之外，情况往往就是这样，尤其是处于发酵等状态中的所有化合物更是如此。

第二节　论气量计

我把气量计（gazometer ）这个名称赋予我为熔化实验中能够提均匀、持续氧气流的一种风箱而发明并让人建造的一种仪器。默斯尼尔先生和我后来又作了非常重要的改进和增添，将其转变成为一种可以称为通用仪器（universal instrument ）的东西，没有这种仪器，几乎不可能完成大部分极精密的实验。我们给该仪器所赋予的名称，表明它是用来测量经受其检测的气体的体积或数量的。

它由一个三呎长的坚固铁梁DE组成（图版VIII，图1 ），在其两端D和E极牢固地连接着同样用坚固的铁做成的圆片。其横梁不是像常规天平中的横梁那样悬着，而是靠一个磨光了的钢质圆轴F（图9 ）支撑在两个活动的大摩擦轮上，以此大大减少对于摩擦产生的运动的抵抗力，将其转变成为二级摩擦。作为一个附加的预防措施，用抛光水晶片盖住这两个轮子支撑横梁圆轴的部分。整个机械固定在结实的木柱BC（图1 ）的顶上。在横梁的D端，用一条直链悬着放砝码的天平盘P，直链与弧n Do 的弯曲部分相适合，处于为此目的而做成的一个槽里。横梁的另一端即E端，用另一条直链ikm ，这条直链要建造得不会因负载重量的多少而延长或缩短；此链在i 处牢固地固定着一个具有三个分支ai、ci 和hi 的三脚架，这三个分支吊着一个直径约18吋、深约20吋，倒置的锻铜大广口瓶A。这个机械的整体在图版VIII图1 中用透视图描绘出来了；图版IX图2和图4 给出了显示其内部结构的垂直截面图。

环绕广口瓶底部外面，固定着分成格子1、2、3等的外沿，用来放图版IX图6 ⁽¹⁾ 的1、2、3分别描绘的铅砝码。这些东西是在需要很大压力时用来增加广口瓶重量的，这在以后再解释，不过很少有这种必要。圆桶广口瓶A的下面de （图版IX，图4 ）是完全敞开的；但是其上面用一个铜盖abc 封闭住，在bf 处开口，能用开关g 关闭。正如通过查图可以看到的那样，这个盖子置于广口瓶顶部之内几吋的地方，以防止广口瓶在任何时候完全浸于水中被遮没。假若我要再改制这个仪器，我就要让盖子大大压扁，使其几乎成为平的。这个广口瓶或气槽置于装满了水的圆桶状铜容器LMNO（图版VIII，图1 ）之内。

在圆桶状容器LMNO（图版IX，图4 ）的中间，放两个管子st、xy ，使两个管子在其上端ty 相互接近；把这两个管子做成这样一种长度，即比容器LMNO上沿LM高出一点，而且当广口瓶abcde 触及底部NO时，其上端约有半吋进入通向活塞g 的锥状孔b 之中。

图3 描绘的是容器LMNO的底部，在其中间焊有一个中空的半球形小帽，可以将其看成倒置的漏斗的大端；st、xy （图4 ）这两个管子在s 和x 处配在这个小帽上，并且以这种方式与管子mm、nn、oo、pp （图3 ）连通，这些管子水平地固定在容器的底上，并且全部结尾于和连接于球帽sx 。这些管子中的三根延伸至容器的外面，如图版VIII图1 所示，图中标有1、2、3的第一个管子，其标有3的一端插入中间活塞4，与广口瓶V相连，广口瓶A位于小气体化学装置GHIK的隔板上，GHIK的内部如图版IX图1 所示。第二个管子从6至7紧靠容器LMNO的外侧，延伸至8、9、10处，并且在11处与广口瓶V的下面相连。这两个管子中的前者是打算用来把气体送进机械的，后者则是打算用来导入供广口瓶中做试验用的少量气体的。根据气体所受压力的程度，它要么进入机械，要么从机械中出来；这个压力通过用砝码使天平盘P载重的或少或多而随意改变。当气体导入机械之中时，压力就减小，甚至变成负的；但是，当要排出气体时，就要用发现是必须的力度去产生压力。

第三个管子12、13、14、15打算用来将空气或气送至燃烧、化合或者其他任何需要空气的实验所必需的地方或装置。

要解释第四个管子的用途，我必须开始某些讨论。假设容器LMNO（图版VIII，图1 ）装满了水，广口瓶A部分装气、部分装水；显然，盘P中的砝码可以校准到使盘的重量与广口瓶的重量之间严格处于平衡，以便使外面的空气不至于进入广口瓶，气体也不至于从广口瓶逸出；在这种情况下，水在广口瓶内外都将严格处于相同的水平面。相反，假若盘P中的重量被减少，那么广口瓶就将承受其自身向下的重力，水在广口瓶内就将比在广口瓶外低；在这种情况下，所包含的空气或气体受压缩的程度就将超过内部空气所受压缩的程度，这超过的程度正好与水柱的重量成比例，等于内外水面之差。出自这些考虑，默斯尼尔先生设计了一种确定广口瓶中所容纳的空气在任何时候所受压力的确切程度的方法。为此目的，他用一个玻璃双虹吸管19、20、21、22、23，在19和23处牢固地黏合住。此虹吸管的19端自由地与机械内容器中的水接通，23这一端则与圆桶状容器底部的第四个管子相通，因而靠垂直的管子st （图版IX，图4 ）与广口瓶中所盛空气接通。他还在16这个地方（图版VIII，图1 ）黏合了另一个玻璃管16、17、18，此管与外面的容器LMNO中的水接通，在其上端18与外面的空气相通。

显然，通过这几个装置，水在管子16、17、18中必定与在池子LMNO中处于同一个水平面；相反，在支管19、20、21中，它必定随广口瓶中的空气所受的压力比外部空气所受压力的大或小而处于或高或低的位置。为确定这些差值，将分成吋和吩的一个黄铜刻度尺固定在这两个管子之间。易于想象，由于空气以及所有其他弹性流体经浓缩必定在重量上会增加，因此必须知道它们缩合的程度以能计算它们的量并将其体积的计量单位变换成为相应的重量单位；这个目的打算用现在描述的装置来达到。

但是，要确定空气或气体的比重，弄清它们在一已知体积中的重量，就必须知道它们的温度以及它们存在于其下的压力程度；这由牢固地粘接在拧进了广口瓶A的盖子之中的黄铜套中的一个小温度计来完成。图版VIII图10 描绘的便是这个温度计，图版VIII图1 和图版IX图4的24、25 描绘了它所处的位置。水银球处于广口瓶A的内部，有刻度的杆则高出盖子的外面。

气量法的实践假若没有比以上描述的更进一步的措施的话，仍然会苦于很大的困难。当广口瓶A沉入池子LMNO的水中时，它必定失去与它所排出的水的重量相等的重量；因此，它对于所盛空气或气体的压缩必定按比例减小。所以，实验过程中由此机械所提供的气体在快要结束时的密度，将与其开始时的密度相同，因为其比重在不断减小。果然不错，这个差值可以通过计算来确定；不过，这引起的数学探索必定会使这种装置的使用变得既麻烦又困难。默斯尼尔先生已经通过下列装置对这种不便进行了补救。让一个正方形铁杆26、27（图版VIII，图1 ）垂直并高于横梁DE的中间。此杆穿过中空的黄铜盒28，黄铜盒敞口，可以填铅；把此盒做得可以靠一个在齿轨上运动的齿轮沿杆滑动，以便升高或降下盒子，并将其固定在被认为是适当的地方。

当杠杆或横梁DE处于水平状态时，此盒不倾向于任何一边；但是当广口瓶A沉进池子LMNO使横梁向这边倾斜时，灌了铅的盒子28就越过支承中心，显然必定倾向广口瓶一边，增加它对所盛的空气的压力。这是按盒子向27升高的比例增加的，因为力借杠杆起作用，而同样的重量所施加的力随杠杆的长度按比例增大。因此，沿杠杆26、27移动盒子28，我们就能增加或减小打算对于广口瓶的压力所做的较正；经验和计算都表明，这恰恰可以补偿在各种程度的压力下广口瓶中失去的重量。

我迄今还没有解释这个机械的用途中的最重要的部分，这就是用它确定实验过程中所提供的空气或气体的量的方式。要极精确地确定此量以及由实验给机械提供的量，我们已将分成度和半度的铜扇lm 固定在横梁E（图版VIII，图1 ）臂终端的弧上，因此铜扇与横梁一起运动；用固定的指针29、30测量横梁的这一端的降低，该指针在其终端有一个指示百分之一度的游标。

上述机械的不同部分的全部细节在图版VIII 中描述如下：

图2 是沃康松（Vaucanson）先生发明的，用来悬挂图1中的天平盘或盘子P的直链；不过由于此链随着负荷的多少而延长或缩短，因此它不适合悬挂图1中的广口瓶A。

图5 是承受图1中的广口瓶A的链ikm 。此链完全是由磨光了的铁板彼此交错并用铁钉夹起来形成的。此链不会由于它所承受的任何重量而在任何可感觉的程度上延长。

图6 ．广口瓶A借以挂在天平上的三脚架，即三分岔蹬形物，螺钉用来将其固定在某个精确垂直的位置上。

图3 ．垂直于横梁的中心而固定、带有盒子28的铁柱26、27。

图7和图8 ．摩擦轮，带有水晶片z作为接触点，以避免天平横梁轴的摩擦。

图4 ．支托摩擦轮轴的金属片。

图9 ．杠杆或横梁的中部，带有它在其上运动的轴。

图10 ．测定广口瓶中所盛空气或气体温度的温度计。

当要使用这个气量计时，要在池子或外部容器LMNO（图版VIII，图1 ）中把水灌至确定高度，这个高度应当在一切实验中都相同。应当在天平横梁处于水平状态时取水位；此水位当广口瓶处于池子底部时，由于它排出水而增加，并随广口瓶升至其最高处而减小。然后我们就通过重复试验，尽力发现盒子28必须固定在什么高度使压力在横梁所处的一切情况之下都相等。我差不多就要说到，由于这种校正并非绝对精确；于是四分之一甚或半吩之差就无足轻重。盒子28的这个高度对于每一种压力程度皆不相同，而是根据这个程度是一、二、三或更多时而变化。所有这些都应当极有条理极精确地记下来。

接下来我们取一个装得下八或十品脱的瓶子，通过称量它能容纳的水极精确地测定其容量。将此瓶翻转底朝上，在气体化学装置GHIK（图版VIII图1 ）的池子中充满水，将其口置于装置的隔板上代替玻璃广口瓶V，将管子7、8、9、10、11的11这一端插入其口内。将机械固定在压力为零的状态，精确观察指针30在扇面ml 上所指示的度数；然后打开活塞8，稍稍压住广口瓶A，迫使空气完全充满瓶子。马上观察指针在扇面上指示的度数，我们同时计算与每一度相应的立方吋数。然后，我们同样谨慎，以同样方式装满第二、第三等等瓶子，甚至用不同大小的瓶子重复同样的操作若干次，直至最后精确注意我们全部弄清广口瓶A的确切限度或容量；不过，最初将其精确做成圆桶形的较好，这样我们就避免了这些计算和估计。

我描述的这种仪器是工程师兼物理仪器制造者小梅格尼（Meignie，Jr.）先生极精确地用非凡的技能建造的。由于用于许多目的，因此它是一种极有价值的仪器；的确，没有它，许多实验几乎都不能完成。由于在许多实验，譬如水和硝酸形成的实验中，绝对必须使用两个相同的机器，因此它就变得昂贵了。在目前化学的先进状态下，对于按照数量和比例以必要的精确性弄清物体的分析和合成来说，极昂贵和复杂的仪器就成为必不可少的了；尽力简化这些仪器并使其费用较低当然很好；但是，这决不应当以尽力牺牲其使用的方便为代价，更不用说以牺牲其精度为代价了。

第三节　测量气体体积的某些其他方法

前一节所描述的气量计，对于一般在实验室里用于气体的测量来说，过于昂贵和复杂，而且它甚至不适合全部这种情况。在许多系列的实验中，必须使用更简单更易于适用的方法。为此目的，我将描述我在拥有气量计之前曾使用并且在我的实验的常规过程中优先于它而仍然在使用的手段。

假设在某个实验之后，置于气体化学装置隔板上的广口瓶AEF（图版IV，图3 ）的上部盛有既不能被碱又不能被水吸收的气体残留物，我们要弄清此残留物的量。我们首先必须用纸条分成若干等分围贴在广口瓶上，极精确地标明汞或水在广口瓶中所升至的高度。如果我们一直是用汞操作的，那么我们就由导入水排出汞开始。将一个瓶子完全充满水，这就容易办了；用你的手指将其堵住，把它翻转过来，将其口插入广口瓶的边缘之下；然后再将瓶体翻转，汞靠其重力落入瓶中，水在广口瓶中升高，占据汞原来所占据的位置。这一完成，就将水注入池子ABCD，使汞面上保持约一吋水；然后将盘子BC（图版V，图9 ）放到广口瓶之下，将其移往水池（图1和图2 ）。这时我们把气体转入另一个按照后面要描述的方式事先已经刻上了标度的广口瓶之中；于是，我们就用气体在刻有标度的广口瓶中所占据的程度来判断其数量或体积。

还有另一种确定气体体积的方法，这种方法既可以用上述方法代替，又可以用作对这种方法的校正或证明。在将空气或气体从用纸条作标记的第一个广口瓶转入刻有标度的广口瓶中之后，将刻有标度的广口瓶瓶口翻转，精确地将水注入至标记EF（图版IV，图3 ）处，称量此水，并将法衡制每70磅折算成一立方呎或1728立方吋的水，我们就确定了它所盛空气或气体的体积。

为此目的而给广口瓶刻标度的方式极为容易，我们应当准备几个不同尺寸的广口瓶，如遇事故甚至每种尺寸的都应当准备几个。取一个高而细有结实玻璃广口瓶，在池子（图版V，图1 ）里充满水，置于隔板ABCD上；对于这个操作我们应当一直使用同一个地方，以便隔板的高度总是完全相同，这样，就将避免这个过程容易出现的几乎是仅有的误差。然后，取一个正好装得下6盎司3格罗斯61格令水，相当于10立方吋的细口管形瓶。如果你没有正好这么大的管形瓶，就挑一个稍大一点的，滴一点熔蜡或松香将其容量减小至需要的大小。这个瓶子用作校正广口瓶的标准。让此瓶中所容纳的空气进入广口瓶，在水下降正好到达的地方做一个标记；再加一瓶空气并记下水的位置，依此重复，直至所有的水都被排出。极为重要的是，在此操作过程中，管形瓶和广口瓶要保持与池子中的水相同的温度；由于这个原因，我们必须尽可能地避免把手放在二者中的任何一个上；如果我们怀疑它们被加热了的话，就必须用池子中的水将其冷却。此实验过程中，气压计和温度计的高度无关紧要。

这样一确定了每十立方吋的标记，我们就用金刚钻刀在其一侧刻上一个刻度。玻璃管以同样方式刻上标记供汞装置中使用，不过它们必须划分成为立方吋和十分之一立方吋。用来校正这些玻璃管的瓶子必须装得下8盎司6格罗斯25格令汞，这正好相当于一立方吋的该金属。

用刻有标度的广口瓶确定空气或气体体积的方法，具有不需要校正广口瓶内和池子中水面高度差的优点；但是它需要根据气压计和温度计的高度进行校正。不过当我们通过称量广口瓶在标记EF以下能容纳的水来确定空气的体积时，必须进一步校正池子中的水面与广口瓶内水上升的高度之差。这将在本章的第五节解释。

第四节　论使不同气体彼此分离的方法

由于实验常常产生二、三种或更多种气体，因此必须能够将这些气体彼此分离，以便我们可以确定每种气体的数量和种类。假设在广口瓶A（图版VI，图3 ）之下容纳有一些混合在一起并处于汞之上的不同气体；像前面指出的那样，我们由用纸条给汞在玻璃瓶中所处的高度作标记开始；然后将约一立方吋水导入广口瓶中，它将浮在汞面上。如果气体混合物含有任何盐酸气或亚硫酸气，那么，由于这两种气体，尤其是前者具有与水化合或被水吸收的强烈倾向，因此迅速、大量的吸收立即发生。如果水只微量吸收不到与自身体积相等的气体，那么我们就断定，该混合物既不含盐酸气和硫酸气，也不含氨气，而是含碳酸气，水只吸收其自身体积的碳酸气。为弄清这个猜想，导入一些苛性碱溶液，碳酸气将会在几小时之内逐渐被吸收；它与苛性碱或草碱化合，剩下的气体几乎完全不含任何感觉得到的碳酸气残留物。

在每一个这种实验之后，我们必须细致地贴上纸条标明汞在广口瓶内所处的高度，纸条一干就涂上清漆以便它们被置于水装置之中时不会被冲掉。也有必要记下每个实验终结时池子中和广口瓶中的汞面之差，以及气压计和温度计的高度。

当所有能被水和草碱吸收的气体都被吸收之后，让水进入广口瓶取代汞；如前一节所述，池子中的汞就会被一两吋的水所覆盖。此后，用平盘BC（图版V，图9 ）将广口瓶移往水装置之中；剩下的气体的量要通过将其转进有刻度的广口瓶之中来确定。此后，通过小广口瓶中的实验小规模地检验它，几乎就确定了该气体的本质。例如，将一支点燃的小蜡烛导入充满气体的小广口瓶（图版V，图8 ）；如果小蜡烛不马上熄灭，我们就断定该气体含有氧气；而且，按火焰的亮度，我们可以判断它所含的氧气比大气所含的是多还是少。相反，如果小蜡烛立即熄灭，我们就有强有力的理由推测，该残留物主要由氮气组成。如果蜡烛一靠近，气体就着火并且在表面带着白色火焰平静地发光，我们就断定它大概是纯氢气；如果火焰是蓝色的，我们就断定它由碳化氢气组成；如果它突然爆燃着火，那么它就是氧气和氢气的混合物。另外，如果一份残留物一与氧气混合就产生红烟，我们就断定它含亚硝气。

这些初步的试验给出了有关该气体的性质和混合物的本质的某些一般性知识，但却不足以确定组成它的几种气体的比例和数量。为此目的，必须使用一切分析方法；而且，为了适当地针对这些方法，用上述诸方法先做一个近似处理是极有用的。例如，假定我们知道残留物由氧和氮气混合组成；就把一定的量即100份放进一个十或十二吩直径的刻度管中，导入硫化草碱溶液与气体接触，让它们在一起放几天；硫化草碱吸收全部氧气，使氮气处于纯态。

如果已知它含有氢气，就把一定量的残留物与已知比例的氢气一起导入伏打（Volta）量气管中；用电火花使它们一起爆燃，逐次加进另外的氧气，直至不再发生爆燃，并产生最大可能的减少。此过程形成水，而此水又立即被装置的水所吸收；但是，如果氢气含有炭，则同时形成碳酸，碳酸并不如此迅速地被吸收；通过摇动帮助其吸收，就易于确定其量。如果残留物含有亚硝气，那么加氧气与之化合成为硝酸，我们差不多就可以根据这种混合物的减少来确定其量了。

我所讲的仅限于这些一般的例子，这些例子足以给出这种操作的概念；一整本书也不会用来解释每一个可能的情况。通过长期的经验熟悉气体分析是有必要的；我们甚至必须承认，它们彼此之间大都具有如此强的亲和力，以致我们并不总是有把握将它们完全分离。在这些情况下，我们必须按照每一种可能的观点使我们的实验多样化，给化合物加进新的试剂，使其他试剂不介入，继续我们的试验，直至我们确信我们的结论真实精确为止。

第五节　论根据大气压对气体体积进行的必要校正

一切弹性流体都可与它们所负载的重量成比例地压缩或凝缩。也许，由一般经验所确定的这条定律，在这些流体处于几乎足以使它们处于液体状态的某种凝缩程度之下时，或者处于极稀薄状态或凝缩状态时，可以允许有某种不规则性；不过，我们用我们的实验所处理的大多数气体，很少达到这两个极限中的任何一个。我对于可与压在其上的重量成比例地压缩的气体的这个命题的理解如下：

气压计是一般所知的一种仪器，严格说来是一种虹吸管ABCD（图版XII，图16 ），其AB支管盛满汞，而CD支管则充满空气。如果我们假定支管CD无限延伸直至它与我们大气的高度相等，我们很容易就可以想象，气压计实际上就是一台天平，其中的汞柱与相同的重量的空气柱处于平衡状态。不过，不必把支管CD延长到这样的高度，因为很显然，气压计陷于空气之中，汞柱AB将同样与相同直径的空气柱处于平衡状态，不过支管CD在C处被截断，CD部分完全被拿开了。

与从大气的最高部分到地球表面的空气柱重量相平衡的汞的平均高度，在巴黎市的较低部分大约是28法吋（French inch）；换言之，在巴黎的地球表面的空气上面，通常压着与高度为28吋的汞柱的重量相等的重量。在本书的几个部分中谈到不同气体时，譬如说到在28吋压力下立方呎的氧气重1盎司4格罗斯时，必须以这种方式理解我所讲的。此汞柱的高度被空气压力所承载，随我们在地球表面，确切地说是在海平之上被升高的程度而降低，因为汞只能与它上面的空气柱形成平衡，该空气柱一点也不受其平面之下的空气影响。

汞以什么比率与其海拔成比例地下降呢？就是说，几个大气层按什么定律或比率在密度上减小呢？这个曾经锻炼了上个世纪的自然哲学家们的独创性的问题，由以下实验加以阐明。

如果我们取一个玻璃虹吸管ABCDE（图版VII，图17 ），其E端封闭、A端敞开，导入几滴汞截断支管AB与支管BE之间的空气流通，那么，BCDE中所含空气显然就与所有周围的空气一样，受与28吋汞相等的空气柱重量之压。但是，如果我们往支管AB中注入28吋汞，那么很清楚，支管BCDE中的空气就将受与两倍28吋汞，即大气重量两倍的重量相等的重量之压；经验表明，在这种情况下，所含空气不是充满从B到E的管子，而是只占据从C到E的管子，即正好是它以前所占空间的一半。如果我们往支管AB中最初的汞柱上另外再加两个28吋，则支管BCDE中的空气就将受大气重量的四倍，即28吋汞重量的四倍之压，那么它就只会充满从D到E的空间，正好是它在实验开始时所占空间的四分之一。从这些可以无限变化的实验，已经推演出一条似乎可适用于一切永久弹性流体的一般的自然定律，即它们的体积与压在其上的重量成比例地减小；换言之：“所有弹性流体的体积与压缩它们的重量成反比。”

为了用气压计测量山的高度所做的实验进一步证实了这些推演的真实性；即使假定它们在某种程度上不精确，这些差异也极小，在化学实验中可以认为它们无足轻重。一旦完全理解了这条弹性流体压缩定律，就可以不费力地将其用于关于气体体积与其压力关系的气体化学实验中所必需的校正。这些校正有两种：一种与气压计的变化有关，另一种则是针对池中所容纳水柱或汞柱的。我将从最简单的情况开始，用例子尽力解释这些。

假设得到100立方吋氧气，氧气处于温度计的10º（54.5º）和气压计的28吋6吩，需要知道这100立方吋的气体在28吋 ⁽²⁾ 的压力下会占据多大体积，以及100吋氧气的重量是多少？令气压计是28吋时这种气体所占据的未知体积即未知吋数受x 之压；由于体积与压在其上的重量成反比，我们就有以下陈述：100立方吋与x 成反比，就如同28.5吋压力比28.0吋一样；或者直接就是28︰28.5∷100︰x＝101.786——立方吋，在28吋气压计压力时；这就是说，在气压计为28.5吋时占据100立方吋体积的同样的气体或空气，在气压计为28吋时将占101.786立方吋。计算占据100立方吋的这种气体在28.5吋气压计压力下的重量同样容易；例如，由于它相当于压力为28吋的101.786立方吋，由于在此压力和温度为10º（54.5º）时每立方吋氧气重半格令，由此得出，在28.5气压计压力下，100立方吋必定重50.893格令。这个结论可以更直接地形成，因为，由于弹性流体的体积与其压力成反比，其重量必定就与同样的压力成正比：因此，由于28吋压力下100立方吋重50格令，于是我们就有以下陈述来确定28.5气压计压力下100立方吋同样气体的重量，28︰50∷28.5︰x，即未知量，＝50.893。

下列实例较为复杂。假设广口瓶A（图版XII，图18 ）的上部ACD盛有一定量的气体，广口瓶CD以下部分装满汞，整个广口瓶竖立于盆或槽GHIK之中，槽内盛汞至EF，并假设广口瓶中CD汞面与池中汞面EF之差为6吋，而气压计位于27.5吋。由这些数据显然可见，ACD中所含空气受大气重量之压，此大气重量由于汞柱CE的重量而减少，即减少27.5－6＝21.5吋气压计压力。因此，此空气受压小于大气处于气压计的普通高度时所受之压，所以它所占据的空间就比它在处于普通压力下时处占空间大，而差值恰恰就与压重之差成正比。那么，如果测量ACD发现它是120立方吋的话，那么它必须折算成它在28吋的普通压力下所占体积。这由以下陈述完成：120︰x 即未知体积，∷21.5︰28反比；这就给出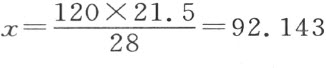 立方吋。

在这些计算中，我们可以将气压计中汞的高度以及广口瓶和池中平面之差换算成为吩或吋的十进小数；不过，我更喜欢后者，因为它更易于计算。由于在这些经常出现的运算中简化方法极有用处，我已经在附录中给出了一个表，将吩和吩的小数换算成为吋的十进小数。

在用水装置完成的实验中，我们必须估计和考虑到在池子中的水面之上广口瓶内水的高度差，而作类似的校正以获得严格精确的结果。不过，由于大气压是用汞气压计的吋和吩表示的，由于同类量才能一起计算，因此，我们必须把观察到的水的吋数和吩数换算成汞的相应高度。我已经在附录中给出了供这种换算用的表，假定汞比水重13.5681倍。

第六节　论与温度计度数有关的校正

在确定气体重量的过程中，除了像前节指出的那样，要将这些气体换算为气压计压力的平均数之外，我们还必须将它们换算为标准的温度计温度；因为一切弹性流体皆热胀冷缩，所以它们在任何确定体积中的重量都易于发生很大的变动。由于10º（54.5º）的温度是夏热冬冷的中间值，是地下场所的温度，也是在所有季节中最易于接近的温度，因此我已经选择此温度作为我在这种计算中将空气或气体换算成的平均值。

德·吕克先生发现，冻点和沸点之间分成81度的汞温度计的每一度，使空气增加其体积的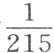 份；对于列氏温度计的每一度来说，是 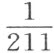份，该温度计在这两点之间分成80度。蒙日先生的实验似乎表明，氢气的这种膨胀较小，他认为它只膨胀 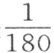。迄今，我们尚无任何发表了的有关其他气体膨胀率的精确实验；不过，从已经做了的试验来看，它们的膨胀似乎与大气的膨胀无多大差别。因此，直至进一步的实验给我们提供关于这个主题的更好信息为止，我都可以当然地认为，对于温度计的每一度而言，大气膨胀 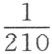份，氢气膨胀 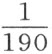份；不过，由于这一点尚极不确定，我们应当总是在尽可能接近10º（54.5º）的标准中操作；用这种方式，通过换算成普通标准来校正气体的重量或体积的过程中产生的误差就将成为极不重要的了。

这种校正值的计算极为容易。把观察到的体积除以210，再用10º（54.5º）以上或以下的温度度数乘商。当实际温度在标准温度之上时此校正值为负，当实际温度在标准温度之下时此校正值为正。使用对数表，这种计算就被大大简化了 ⁽³⁾ 。

第七节　计算与压力和温度的偏差有关的校正值的例子

实　例

竖立于水装置中的广口瓶A（图版IV，图3 ）中，盛有353立方吋空气；广口瓶内EF水面处于池子中的水之上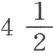 吋，气压计处于27吋 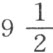吋，温度计处于15º（65.75º）。在空气中燃烧了一定量的磷，便产生了凝固的磷酸，燃烧后的空气占295立方吋，广口瓶中的水处于池子中的水之上7吋处，气压计处于27吋 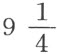吩，温度计处于16º（68º）。需要由这些数据确定空气在燃烧前后的实际体积以及此过程中吸收的量。

燃烧前的计算

燃烧前广口瓶中的空气是353立方吋，不过这只是处于27吋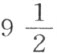 吩的气压计压力之下，将此压力换算成十进制小数，就是27.79167吋；我们必须从中减去 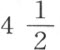吋水的差值，这相当于压力计的0.33166吋；因此，广口瓶中空气的真实压力是27.46001。由于弹性流体的体积按压重的反比减少，我们就有以下陈述，将353吋换算成为空气在28吋气压计压力下所占体积。

353︰x ，即未知体积，∷27．46001︰28。于是有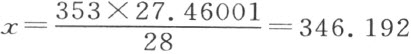， 立方吋，这就是同量的空气在气压计为28吋时所占体积。

此校正了的体积的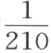 份是1.65，由此得出，对于标准温度之上每五度来说，即为8.255立方吋；而且，由于此校正值是负的，因此，空气在燃烧前实际校正了的体积是337.942吋。

燃烧后的计算

通过对燃烧后的空气体积作类似计算，我们发现其气压计压力为27.77083—0.51953＝27.25490。因此，为得到在28吋压力下空气的体积，295︰x ∷27.77083︰28反比；即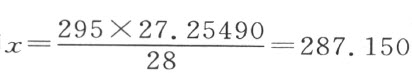 。此校正了的体积的 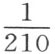份是1.368，它乘以6度的温度计差值，就得到对于温度的负校正值为8.208，剩下空气在燃烧后实际校正了的体积278.942吋。

结　果

第八节　确定不同气体绝对重量的方法

取一个能盛17或18品脱或半立方呎的大球形瓶A（图版V，图10 ），有一个黄铜帽bcde 牢固地连接在球形瓶瓶颈上，黄铜帽上用严实的螺旋固定着管子和活塞fg 。此装置用图12 中单独描绘的双螺旋与图10 中的广口瓶BCD连通，广口瓶必须在容积上比球形瓶大若干品脱。此广口瓶顶部开口，配有黄铜帽hi 和活塞lm 。图11 单独描绘的是这些活塞中的一个。

我们首先将球形瓶盛满水，并对满瓶和空瓶进行称量，以确定球形瓶的确切容量。放空水时，从瓶颈de 插进一块布将其擦干，最后残余的潮气用空气泵抽一两次除去。

当要确定任何气体的重量时，按以下所述使用此装置：用活塞fg 的螺丝将球形瓶A固定到空气泵的板子上，活塞开着；球形瓶要尽可能完全抽空，用附配在空气泵上的气压计仔细观察抽空的程度。形成真空时，关上活塞fg ，以一丝不苟的精确性确定球形瓶的重量。然后将其固定到广口瓶BCD上，我们让此广口瓶置于气体化学装置（图1 ）隔板上的水中；广口瓶要盛满我们打算称量的气体，然后打开活塞fg 和lm ，气体上升进入球形瓶，而池子中的水同时上升进入广口瓶。为避免极麻烦的校正，在这第一个部一分的操作过程中，有必要将广口瓶沉入池子中至广口瓶中的水面为止，无须精确一致。再关上两个活塞，将球形瓶从它与广口瓶的联结处旋开取下，仔细称重；此重量与抽空了的球形瓶的重量之差，就是球形瓶中所盛空气或气体的精确重量。将此重量乘以1728，即乘以1立方呎中的立方时数，再将积除以球形瓶中所容立方吋数；商就是用来做实验的1立方呎气体或空气的重量。

必须精确说明上述实验过程中气压计的高度和温度计的温度；根据这些，1立方呎的最终重量就易于校正为28吋和10°的标准，如前节所指出的那样。形成真空之后留在球形瓶中的少量空气也必须注意，这用附配在空气泵上的气压计容易确定。例如，如果该气压计保持在真空形成之前它所处的高度的百分之一处，我们就断言原来所盛空气的百分之一仍留在球形瓶中，因此，只有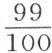 的气体从广口瓶进入球形瓶。

————————————————————

(1) 英文版误为“图3”。——C

(2) 根据法呎与英呎之间给定的114比107的比例，法制气压计的28吋等于英制气压计的29.83吋。在附录中将会找到对于将本书中所使用的法制衡量和度量换算成为相应的英制单位的说明。——E

(3) 当使用华氏温度计时，每一度引起的膨胀必定较小，即按1︰2.25的比例，因为列氏温标的每一度相当于华氏2.25度；因此，我们必须除以472.5，再按以上所述结束其余的计算。——E