第一章 导 言
·Chapter I Introduction·
傅立叶之所以能取得富有如此深刻内容的成就,正如撰写傅立叶传记的两位作者所说,这只有赋有生动的想象力和具有适合其工作的清醒的数学哲学头脑的数学大师才能达到。从傅立叶的著作中,我们看到:他坚信数学是解决实际问题的最卓越的工具。这一见解是傅立叶一生从事学术研究的指导性观点,而且已经成为数学史上强调通过研究实际问题发展数学(包括应用数学和纯粹数学)的一派数学家的代表性格言。

古老的欧塞尔市通向荣纳河的一条街道
第一节 本著作目的的表述
1 热的作用服从于一些不变的规律,如果不借助于数学分析就不可能发现这些规律。我们即将要阐明的这个理论的目的就是要论证这些规律;它把关于热传导的所有物理研究都归结为其基础已由实验所给出的那些积分运算问题。由于热的作用永远存在,它充斥于一切物质和空间之中,它影响工艺过程,并发生在宇宙的一切现象之中;因此,没有任何主题比它与工业和自然科学的进步具有更广泛的联系了。
当热在一个实体的不同部分之间不均匀地分布时,它倾向于达到平衡,并且慢慢地从较热部分传到次热部分;同时它在表面耗散,并且耗散在介质或空间中。作用在物体表面的这种自发辐射倾向于不断改变它们不同点的温度。假定初始温度已知,那么,热传导的问题就在于确定在一给定时刻一物体在每一点的温度是怎样的。下面的例子将更清楚地弄清这些问题的本质。
2 如果我们使一个直径很大的金属环的同一部分受一个热源持续而均匀的作用,那么,最靠近热源的分子将首先被加热,并且经过一定时间之后,这个固体的每一点都将获得非常接近于它所能达到的最高温度。这个极限温度或最高温度在不同点上是不同的;它随它们离受热源直接作用的那一点愈远而愈低。
当这些温度变成永恒不变时,热源在每一时刻内提供恰好补偿在这个环的外表面的所有点上所耗散的热量。
如果现在撤掉这个热源,热将继续在这一固体内传导,但是,在介质和空间中所失掉的热,就再也不会像以前那样由这个热源提供补偿了,因此,所有温度都将变化,并且不断减少,直到它们变得与周围介质的温度相等为止。
3 当温度永恒不变,并且保留热源时,如果在环的中周的每一点上作一个垂直于环平面的纵坐标,它的长度与那一点的固定温度成正比,那么,过这些纵坐标端点的曲线就表示这些温度的永恒状态,并且,很容易用分析来确定这条曲线的性质。应当注意,由于假定与中周垂直的同一个截面的所有点的温度明显相等,所以假定环是很细的。当热源撤走时,界定这些与不同点的温度成正比的纵坐标的曲线,就不断改变它的形式,问题在于用一个方程表示这条曲线的这种可变形式,因此,就在于用单个公式概括这一固体的所有连续状态。
4 设z是中周上一点m的不变温度,x是这一点到热源的距离,即是包含在点m和对应于热源位置的点o之间的这段中周弧的长度;z是点m依靠热源的恒定作用所能达到的最高温度,这一永恒温度z是距离x的一个函数f(x)。这个问题的第一部分在于确定表示这个固体永恒状态的函数f(x)。
考虑当热源一移开时继前一个状态的下一个变化状态;用t表示自热源撤除后所经历的时间,用v表示t时后点m的温度值。量v则是距离x和时间t的某个函数F(x,t);这个问题的目的是要找到这个函数F(x,t),我们现在仅仅只知道这个函数的初始值是f(x),因此我们应当有方程f(x)=F(x,0)。
5 如果我们把一个形如球或立方体的同质实体放进一种保持恒温的介质中,把它持续浸泡很长时间,那么,它将在它的所有点上都达到与这种流体相差无几的温度。假定取出这一物体,把它转移到转凉的介质中去,那么,热将开始在其表面耗散;这一物体不同点的温度也会明显地不同,如果我们假定它被平行于它的外表面的面分成无穷多个薄层,那么,在每一时刻,每一薄层就向包围它的薄层传送一定量的热。如果设想每一分子带有一个单独的温度计,它表示它在每一时刻的温度,那么,这一固体的状态就时刻由所有这些温度计所测得的高度的变化系统来表示。有必要用解析公式表示这些连续变化,以便我们能够在这一给定时刻知道由每一个温度计所标明的温度,并且比较同一时刻内两个相邻薄层之间所流过的,以及进入周围介质的热量。
6 如果这一物体是球状的,并且我们用x表示这一物体某一点到球心的距离,用t表示自冷却开始后所经历的时间,用v表示点m的变化温度,那么容易看出,位于与球心距离相同的点有相同的温度v。这个量v是半径x和时间t的某个函数F(x,t);无疑,当我们假定t为零时,无论x是什么值,v都是常数;因为由假定,在取出的一瞬间,所有点的温度都相同。问题在于确定那个表示v值的x和t的函数。
7 接下来应该注意,在冷却期间的每一时刻,一定热量通过外表面而逃逸,并进入介质。这个量值不是不变的;它在冷却开始时最大。然而,如果我们考虑半径为x的内球面的变化状态,那么我们容易看到,在每一时刻肯定有一定热量穿过那个球面,并且经过这一物体距球心更远的那一部分。热的这一连续流动同它经过外表面的流动一样,是可变的,并且两者是可以相互比较的量;它们的比是其变化值为距离x和历经时间t的函数的数。有必要确定这些函数。
8 如果长时间在介质中浸泡所加热,并且我们想计算其冷却率的这一物质,是一个立方体,如果我们取这一立方体的中心为原点,取垂直于各面的线为轴,用三个直角坐标x,y,z确定每一点的位置,那么我们看到,在时间t之后,点m的温度v是4个变量x,y,z和t的一个函数。在每一时刻过这一固体的整个外表面所流出的热量是变化的,并且可以相互比较;它们的比是依赖于时间t的一些解析函数,是我们应当确定的表达式。
9 让我们也考察这样一种情况:一个充分粗、无限长、其末端受恒温作用的矩形棱柱,当它周围的空气保持较低温度时,最后达到一个需要确定的固定状态。由假定,在棱柱基底的底截面上的所有点都有相同和永恒的温度。与热源有距离的截面则不同;这个平行于基底的矩形面的每一点得到一固定温度,但是,这在这同一个截面的不同点上是不一样的,在离受空气作用的面更近的点上,温度肯定更低一些。我们还看到,由于这一固体的状态已经变成恒定的,因此,在每一时刻,有一定的热量流过一个已知截面,它们总是相等的。问题在于确定在这一固体的任一已知点上的永恒温度和在一个给定时间内,流过其位置已知的截面的总热量。
10 取棱柱基底的中心为坐标x,y,z的原点,取棱柱本身的轴和垂直于各底边的两条垂线为直角坐标轴:其坐标为x,y,z的点m的永恒温度v,是三个变量的函数F(x,y,z):当我们假定无论y和z取什么值x均为0时,由假设,这个函数有一个常数值。如果由一个面积所界定、由相同物质组成为这一棱柱的这一受热物体一直保持沸水温度,并且浸没在保持溶冰温度的大气中,那么,让我们以在一个单位时间内从一个与单位面积相等的面积中所发出的热量为一个热量单位。
我们看到,在这个矩形棱柱的永恒状态中,在一个单位时间内,流过垂直于轴的某一截面的热量与作为单位的热量有一个确定的比,这个比对所有截面来说是不同的:它是这一截面所位于的距离x的函数φ(x)。需要找到函数φ(x)的一个解析表达式。
11 上述例子足以对我们所谈过的不同问题给出一个精确思想。
这些问题的解使我们认识到,就每一种固体物质来说,热传导的作用都依赖于三个基本量,它们是物质的热容量(capacity for heat),它的自热导率 【1】 (own conducibility)和外热导率(exterior conducibility)。
人们已经观察到,如果同体积不同质的两个物体有相同的温度,并且如果对它们增加相同的热量,那么,温度的增量是不相同的,这两个增量的比是它们热容量的比 【2】 。如此,规定热作用的三个具体要素中的第一个,就被严格地确定了,并且,物理学家们很早就知道几种确定它的值的方法。其他两个要素就不一样了;虽然它们的作用经常被观察到,但是还没有一个严格的理论能精确地区别、定义和测量它们。
一个物体的固有热导率或内热导率(the proper or interior conducibility)表示使热从一个内部分子传递到另一个内部分子的能力。一个固体的外热导率或相对热导率(the external or relative conducibility)取决于热穿过其表面,并从这一物体进入一种已知介质,或者,从这种介质进入这个固体的能力。这后一种性质或多或少地由表面的光洁状态所左右;它也随这一物体所浸入其中的介质而变化;但是内热导率只随这一固体的质而变化。
在我们的公式中,这三个基本量由常数来表示,并且这一理论本身指明适合于测量它们的值的实验。一旦它们被确定,则与热传导有关的一切问题就都只取决于数值分析。关于这些特殊性质的知识可能在物理科学的几种应用中都直接有用;此外,这种知识也是不同物质的研究和描述的一个要素。那些忽视它们与自然界主要作用力之一所具有的这些联系的知识,将是非常不完善的。总的说来,由于这一理论可以给以热的使用为基础的无数工艺实践带来清晰性和完整性,所以,还没有任何一种数学理论比它与国民经济具有更紧密的联系。
12 地球温度问题表明是热理论的最漂亮的应用之一;形成它的一般思想如下。地球表面的不同部分不等地受到太阳光线的作用;其作用强度取决于那一地点的纬度;它在一天的过程中和在一年的过程中也有变化,并且受到其他更不易察觉的不均匀性的影响。显然,地表的变化状态与内部温度的变化状态之间存在着一种必然联系,它可以由理论导出。我们知道,在地表以下的某一深度,在一已知地点的温度无年变:这一永恒的地下温度随这一地点离赤道愈来愈远而变得愈来愈低。地球外壳的厚度相对于地球半径无比地小,因此我们可以不考虑它,而把我们这颗行星看做是一个近球体,它的表面受到这样一种温度的作用,这种温度在一条给定的纬线的所有点上保持不变,而在另一条纬线上则不同。由此推出,每一个内分子也有由它的位置所确定的固定温度。这一数学问题在于找出任一已知点的固定温度,以及日热在射入地球内部时所遵循的规律。
如果我们考虑在我们居住于其表面之上的地壳本身中所相继发生的变化,那么,这种温度的差异性就会使我们更加感兴趣。在每一天和在每一年的期间所反复产生的那些冷暖交替,至今都一直是反复观察的对象。我们现在可以计算它们,并且可以从一个一般的理论推导出经验所教给我们的所有特殊事实。这一问题可简化成这样一个假设:一个巨大球体的每一点都受到周期性温度的作用,那么分析告诉我们,这些变化的强度根据什么规律随深度的增加而减弱,在一给定深度上,年变化或日变化的总量是多少,这些变化的时期是怎样的,怎样从地表所观测到的变化温度推出地下温度的固定值。
13 热传导的一般方程是偏微分方程,虽然它们的形式非常简单,但是,已知的方法 【3】 并不能对它们的积分提供任何一般的形式;因此,我们不能由它们推出某一确定时间之后的温度值。然而,这些分析结果的数值解释是必需的,并且,对于给出分析对自然科学的每一种应用来说,这种数值解释可能是某种非常重要的完善标志。只要尚未得到它,就可以说解仍然是不完全的和无用的,并且,人们想要发现的这一真理深藏在分析公式之中,这丝毫不亚于它原来在物理问题本身中的隐蔽性。我们一直以极大的关注致力于这一目标,我们已经能够克服在我们所处理过的,并且包括热理论的基本原理在内的所有问题中的困难。每一个问题的解都对发现所得到的温度的数值,或者当时间值和变量坐标的值已知时,对发现那些所流过的热量的数值,无不提供简便而精确的方法。因此,我们不仅将给出表示温度值的函数所必须满足的微分方程,而且将以便于数值应用的形式给出这些函数本身。
14 为了使这些解能够是一般的,并且具有与这一问题相同的范围,必要条件是它们应当适合温度的初始状态,这个初始状态是任意的。对这一条件的研究表明,对于不服从于某个不变的规律,并且表示不规则或不连续线段的纵坐标的那些函数,我们可以以收敛级数展开,或者用定积分来表示。这一收获对偏微分方程理论给出一种新的见解,并且通过使任意函数服从于分析的一般过程而扩大它们的应用。
15 剩下来的,还有事实与理论的比较。为着这一目的,我们做了各种精确的实验,这些实验结果是与这些分析的结果一致的,并且赋予这些分析结果一种在看上去受制于如此之多的不确定性的新问题中人们就不情愿赋予的权威。这些实验确证我们由之开始的原理,尽管物理学家们在关于热的本质的假设上众说不一,但是他们都采纳这一原理。
16 温度平衡不仅可以以接触的方式产生,而且长时间处在同一地区的相互分离的物体之间也可以建立温度平衡。这种作用与介质的接触无关;我们已经在真空中观察到它。为了完成我们的理论,有必要考察辐射热在离开物体表面时所遵循的规律。从许多物理学家的观察中和我们自己的实验中可以得出:从一受热物体表面任一点在各个方向上所逃逸出的不同光线的强度,取决于它们的方向与这同一点所在平面所成的夹角。我们已经证明,一条光线的强度随这条光线与面元素所成夹角的缩小而减弱,并且它与那个角的正弦成正比 【4】 。不同的观察已经表明的这个热辐射的一般规律是固体中温度平衡原理和热传导规律的一个必然结果。
这些就是本书所讨论的主要问题;所有这些讨论只有一个目的,那就是清晰地建立热理论的数学原理,并在这一方面跟上实用工艺的步伐和对自然研究的步伐。
17 据以上所述,显然存在一类非常广泛的现象,它们并不由机械力所产生,而仅仅只由热的存在和积累而引起。自然哲学 【5】 的这一部分不可能与动力学的理论有关,它有它本身所特有的原理,并且建立在一种与其他精密科学相类似的方法之上。例如日热,它贯穿到地球内部,并根据一条固定的规律使自己分布于其中,这条规律不依赖于运动规律,也不由力学原理所决定。热的推斥力所产生的膨胀,以及用于测量温度的观察,的确都是动力学的效应,但是当我们研究热传导的这些规律时,它就不是我们所计算的这些膨胀了。
18 还有其他更复杂的自然效应,它们同时依赖于热的影响和引力的影响;因此,太阳的运动在大气和海洋中所引起的温度变化,不断改变空气和水域不同部分的密度。这些物质所服从的这些力的作用,在每一时刻都被一种新的热分布所改变,并且毫无疑问,这个原因引起规则的风和海洋的主要潮流;日月的引力,在大气中只产生勉强可察的作用,不引起一般的位移。因此,为了使这些重大现象服从于计算,有必要去发现物质内部热传导的数学规律。
19 阅读本书时读者会看到,热在物体内达到一种规则排列与初始分布无关,初始分布可以看做是任意的。
热在开始时无论以何种方式分布,变化愈来愈大的这个温度系统都将明显地趋于与只和固体形状有关的一个确定状态相重合。在极限状态下,所有点的温度都同时下降,但各点之间保持相同的比:为了表示这个性质,解析公式就应该包含一些由指数和由类似于三角函数的量所组成的项。
力学的几个问题提供类似的结果,如摆的等时性,发声物体的复共鸣等。普通实验使人们注意到这些结果,以后的分析论证了它们的真正原因。至于那些依赖于温度变化的结果,除非很精密的实验,否则它们就不可能被认识到;但是数学分析已经超过观察,它弥补了我们感官的不足,在某种意义上,它使我们亲眼看到物体内部规则和谐的振动。
20 这些考虑对存在于数的抽象科学和自然原因之间的联系提供了非凡的范例。
当一根金属棒的一端受一个热源的恒定作用,并且其各点都已经达到它的最高温度时,这个固定温度系统就严格对应于一个对数表;数是不同点所在的温度计的标高,对数是这些点与热源的距离。一般来说,热根据不同类型的物理问题所通用的一个偏微分方程所表示的简单规律使自己分布于物体内部。热辐射与正弦表有一种明显的联系,因为,从受热面的同一点出来的射线彼此非常不同,它们的强度严格与各射线的方向与面元素所成夹角的正弦成正比。
如果我们在一个同质固体物质的每一点上能够观察到每一时刻的温度变化,那么,我们就会在这些系列观察中发现那些象正弦和对数那样的循环级数的性质;例如,它们可能在地球近地表的不同点的日变化温度和年变化温度中被注意到。
我们还可以在弹性介质的振动中,在曲线或曲面的性质中,在星体的运动中,以及在光或流体的运动中,认识到这些同样的结果和一般分析的所有主要的基本原理。在无穷级数的展开中和在数值方程的解中所运用的、通过逐次微分所得到的这些函数,也对应着物理性质。这些函数的第一个,或者准确地说称之为流数(fluxion),在几何学中表示一条曲线正切的倾角 【6】 ,在动力学中表示一个运动物体在这一运动发生变化时的速度;在热的理论中,它计量在一个物体的每一点上经过一个已知面所流过的热量。因此,数学分析与可感知的现象有着必然的联系;它的对象不为人的智力所创造;它是宇宙秩序的一个先在要素(a pre-existent element),并且在任何意义上都不是偶然的或者是意外的;整个自然界到处都打上了它的印记。
21 更精确、更丰富的观察必将弄清热效应是否将由尚未察觉的一些原因来修改,热的理论将在它的结果与实验结果的不断比较中获得进一步的完善;它将阐明我们至今尚不能分析的某些重要现象;它将表明怎样确定太阳光线的所有温度计效应,表明不论是在地球内部还是在大气圈的范围之外,不论是在大洋中还是在大气的不同区域中,在这些与赤道不同距离的位置,怎样确定可能观察到的不变或可变的温度。由此导出由热和重力的综合作用所产生的大规模运动的数学知识。同样这些原理将用来测量不同物体的固有热导率和相对导率,以及它们的比热,用来鉴别使固体表面的热辐射发生变化的一切原因,并且用来改进测温仪。
热的理论,将以其基本原理的严格精确性和它所特有的分析困难,并且首先以它应用的广度和有效性,而永远吸引数学家们的注意力;因为它的一切结果都同时与普通物理学,与工艺效果,与家庭习惯和国民经济有关。
第二节 初始定义和一般概念 【7】
22 关于热的本质只能形成一些不确定的假说,但是关于它的效应所服从的数学规律的知识,却与一切假说无关;它仅仅只需要对一些日常观察所表明、由精确实验已确证的主要事实进行细致的考察就够了。
这样,首先有必要陈述一般的观察结果,对分析的所有要素给出精确定义,并建立作为这种分析之基础的原理。
热的作用常常会使所有物体,固体、液体或气体等都膨胀;这是给出其存在证据的性质。只要固体和液体所含的热量增加,它们的体积就增加 【8】 ,热量减少,其体积也随之减少。
当一个同质固体物质的所有部分,如一个金属物体的所有部分,被同等地加热,并且毫无变化地维持同一热量时,它们也具有并保持相同的密度。这一状态由这样一种说法来表示:在这一物体的整个范围内,分子处处都具有相同和永恒的温度。
23 温度计是使得人们能够鉴别它体积的最小变化的物体;它的作用是以一种流体或一种空气的膨胀来测量温度。我们假定我们精确地知道这个仪器的结构、用法和性能。一个各部分被同样加热并保持其热的物体的温度,就是当温度计是并且保持与所研究的这一物体完全接触(perfect contact)时它所标明的温度。
完全接触就是温度计完全浸没在一流体物质中,一般地,就是该仪器外表面没有任何一点不为其温度待测的固体或流体物质的一点所接触。在实验中,并非总是要求一定要严格保持这一条件;但是为了使定义精确,应当这样假定它。
24 我们确定两个固定温度,即由0来表示的溶冰温度(the temperature of melting ice),以及我们用1来表示的沸水温度(the temperature of boiling water):假定水在一个大气压下沸腾,一个大气压由气压表中的水银为0度时,该气压表的某个高度(76厘米)来表示。
25 不同的热量通过确定它们包含一个作为单位的固定量的多少倍而测得。假定有一个确定重量(1千克)的冰块,其温度为0度,通过增加一定的热量,在同一0度温度下转变成水:这样,所增加的这一热量就被看做为测量单位(the unit of measure)。因此,由数C所表示的热量,就等于把温度为0度的1千克冰在同一0度温度下溶解成水时所需要的热量的C倍。
26 要使有一定重量的金属物体,如1千克铁,从0度上升到1度,就必须有一些新的热量增加到这一物体已有的热量中去。表示这一补充热量的数C,就是铁的比热(Spe cific capacity of iron for heat),数C对于不同的物质有非常不同的值。
27 如果一个定质定量的物体(1千克汞)在0度时有体积V,当它达到1度时,也就是说当它在0度时所包含的热量增加一个等于这一物体比热的新热量时,那么它将占有更大的体积V+∆。但是,如果不是增加这个量C,而是增加量zC(z是一个或正或负的数),那么,新的体积就不是V+∆,而是V+δ。现在,实验表明,如果z=½,则体积的增量δ就只有整个增量∆的一半,并且一般地,当增加的热量是zC时,δ的值就是z∆。
28 所增加的热的这两个量zC和C的比z,与两个体积增量δ和∆的比是相同的,它就是所谓的温度比;因此,表示一个物体有效温度的量代表它的实际体积超过其在溶冰温度下所具有的体积的超出量,1代表对应于水的沸点的体积超过对应于冰溶点的体积的整个超出量。
29 物体体积的增量一般与产生膨胀的热量的增量成正比,但是应当注意,这个比仅仅只在所研究的物体所经受的温度远离那些决定它们状态变化的温度的情况下才是精确的。这些结果不一定能应用于所有液体;特别对于水而言,膨胀并不总伴随热的增加。
一般来说,温度是与所增加的热量成正比的数,就我们所考虑的情况而言,这些数也与体积的增量成正比。
30 假定由有一定面积(1平方米)的平面所界定的物体无论以什么方式使其所有点都同样保持恒定温度1,并且假定所说的这一平面接触保持0度的空气:则从这个平面不断逃逸并进入周围介质中去的热,总是由那种作用在这个物体上的恒定原因所产生的热所补充;因此,由h所表示的一定热量在一个确定时间(1分钟)内流过这一平面。
在一个固定温度下,发生在一个单位平面上的一个连续并且总与自身相同的热流的总量h,就是这个物体的外热导率的量度,也就是说是它的表面向空气传热的能力的量度。
这里的空气被认为是以一个已知的匀速连续移动的;但是,若这一气流的速度增加,则传入介质的热量也会发生变化:若介质的密度增加,同一情况亦会发生。
31 如果这一物体的这一恒定温度超过周围物体温度的超出量不是如所假设的那样等于1,而是一个较小的值,那么,所耗散的热量就比h少。正如我们即将看到的,观察结果是,所失掉的这一热量可以看做是明显与这一物体的温度超过空气和周围物体的温度的超出量成正比的。因此在量h已经由受热面为1度,介质为0度的一个实验所确定时;我们得出结论:如果这个面的温度为z,所有其他情况保持不变,则所耗散的这个热量就是hz 【9】 。当z是一个小分数时,我们肯定可以承认这一结果。
32 经过一个受热面而扩散的这一热量的这个h值随不同物体而异;并且,对于同一物体,它也随这个面的不同状态而变化。这一辐射作用随这个面的光洁度的提高而减少;因此,破坏这个面的光洁度,h值会明显增加。如果一个被加热的金属物体的外表面被涂上一层诸如能完全使其失去金属光泽的黑漆,那么,它就会冷却得更快。
33 从一个物体的表面所逃逸的热辐射线自由地穿过真空空间;它们也在大气中传导:它们的方向不为介入空气(interveningair)中的扰动所干扰:它们可由金属镜反射并集中到金属镜的焦点上。高温物体,在被插进一种液体中时,它们仅仅只直接加热它们的表面所与之接触的那些部分的液体。与这一表面不太近的分子不直接受热,气流体则不一样;在它们之中,热辐射线极快地传到很远的地方,或者是这些射线的那一部分自由地穿过大气层,或者是这些气层迅速传播这些射线而不改变其方向。
34 当把这一受热物体放到保持明显不变的温度的空气中时,传导到这些空气中的热就使离这一物体表面最近的流体层更轻;这一气流层受热愈强,它就上升得愈快,并由其他冷气团所补充。这样,在方向垂直、速度随这一物体的温度更高而更快的空气中形成一股气流。由于这个原因,如果这一物体逐渐自行冷却,则这一气流的速度就随温度而减弱,并且,这一冷却规律和这一物体受一定速气流作用的规律不完全相同。
35 当物体被加热到足以漫射强光时,它们的部分辐射热就与能穿过透明固体或流体,并受产生折射的力的支配的那种光相混合。随着这些物体的炽热光焰逐渐减弱,有这种能力的热量也随之减少;我们可以说,对于极不透明的物体而言,即使它们极度受热,也察觉不出来。一个薄透明片几乎拦截所有由剧热金属体所产生的直热;不过,它随被拦截的射线在它之中的积累而成比例地逐渐被加热;因此,若它由冰组成,则它变成液体;但是,若这一冰片受一条光炬的作用,则它允许相当多的热量随光一起穿过。
36 我们曾经用一个系数h作为一个固体外热导率的量度,它表示在一确定时间(1分钟)内从这一物体表面进入空气的热量。假定这一表面有一个确定的面积(1平方米),这一物体的不变温度是1,空气的不变温度是0,并且受热面受一给定的不变速度的气流的作用。这个h值由观察来确定。由这一系数所表示的热量由两个不同的部分所组成,若无极精确的实验,这两部分热量就不可能被测量出来。它们一部分是以接触的方式向外界空气所传递的热;另一部分,比第一部分少得多,是所发射的辐射热。在我们最初的研究中,我们应当假定,当这一固体的温度和介质的温度以同一充分小量增加时,所失去的热量不变。
37 正如我们所注意到的,固体物质的另一个差别是它们可渗透性的大小;这个性质就是它们的固有热导率(conducibility proper):在论述了热的均匀传导和线性传导之后,我们将给出它的定义和精确量度。液态物质也具有从分子到分子的导热性,并且它们热导率的数值随物质的质而变化:但是这个作用难以在液体中观察到,因为温度一变化,它们的分子就会改变其位置。在物质下部受热源作用最大的所有情况中,在这些液体中的热传导主要靠这种不断的位移来进行。相反,同在我们的几个实验中的情况一样,如果热源作用于物质最上层的那一部分,则热转移非常慢,它不引起任何位移,至少当温度的增加不缩小其体积时,如像在接近于状态变化的一些异常情况中所注意到的那样,情况的确如此。
38 对这些主要观察结果的这一解释应当就温度平衡增加一个一般性的注记;这个注记在于这样一点,位于同一区域的不同物体,若它们各部分都是并且保持等加热,则也达到一共同的永恒温度。
假定一个物体M的所有部分都有一无论以什么原因所保持的共同和不变的温度a;如果一个更小的物体m以完全接触的方式与物体M放在一起,则它将被假定为有共同的温度a。
实际上,除非经过无穷时间,否则这个结果就不可能严格地出现:但是这个命题的准确意思是:若物体m在被置于接触中去之前就有温度a,则它将保持这一温度而不发生任何变化。放得使每一个都分别与物体M完全接触的许多其他物体n,p,q,r的情况亦如此:它们都将达到恒定温度a。因此,一个温度计,若相继用于这些不同的物体m,n,p,q,r,则会指示相同的温度。
39 如果物体m的每一部分都被包含在这一固体M中,如在一包壳中而不接触它的任一部分,那么,所讨论的这一作用就既与接触无关又仍然会发生。例如,如果这一固体是一个有一定厚度、由某种外因保持在温度a上,并且包含一个完全排除空气的空间的球形外壳,如果物体m可以被放到这一圆形空间的任一部分中而不接触包壳的内表面的任一点,那么,它将达到共同温度a,更准确地说,如果它已经在球形包壳中,则它将保持这一温度。对所有其他物体n,p,q,r,无论它们是分别地,还是一起放到这同一球形包壳中,并且还无论它们的物质和形状怎样,其结果都一样。
40 我们对热的作用所提出的所有这些模式看来是最简单的并且是与观察最一致的,提出它们的目的在于把这种作用与光的作用作一个比较。正如发光物体发射它们的光一样,互相分离的分子通过空气相互传递它们的热辐射线。
如果在处处密封,并且由某种外因保持固定温度a的一个包壳内,我们假定放进一些不同的物体,并且这些物体与内边缘任一部分均无接触,那么,随这些被放进这一真空空间的物体受热的多少,我们会观察到不同的作用。在第一种情况中,如果我们只放进一个这样的物体,它的温度和包壳的相同,那么,它从它表面各点发射的热和它从包围它的这一固体那里所得到的热一样多,并且通过这种等量交换保持它的初始状态。
如果我们放进第二个物体,它的温度b小于a,那么,它首先会从处处包围它而不接触它的面得到比它所放出的更大的热量、它将越来越被加热,并且通过它的表面吸收比它在第一种情况中所吸收的更多的热。
初始温度b不断升高,它将不停顿地趋近固定温度a,因此,在某时间之后,这个差将变得微乎其微。如果我们在这同一包壳内放进温度比a高的第三个物体,那么就会有相反的作用。
41 所有物体都有通过其表面发射热的性质;它们愈热,它们就发射得愈多;所发射的辐射线的强度随表面状态而发生相当明显的变化。
42 从周围物体得到热辐射线的每一个面,都反射一部分,保留其余部分:未被反射而进入这个面的热,在这一固体中积累;并且,只要它超过由辐射所耗散的量,那么温度就上升。
43 倾向于离开受热物体的辐射线通过一种把它们的一部分反射到这一物体内部的力而在其表面被俘获。阻止入射线经过这个面,并把这些辐射线分成两部分,一部分被反射,另一部分被保留的那个原因,也以同样的方式作用在从这一物体内部指向外部空间的那些射线上。
如果我们通过改变表面状态而增加它反射入射线的力,那么我们同时也增加了朝这一物体内部反射要离开它的辐射线的力。进入这一物质的入射线和通过其表面而发射的辐射线,在数量上相等地减少。
44 如果在这个包壳内同时放进上面所提到过的一些彼此分离且受热不等的物体,那么它们将得到和发射热辐射线,这样,在每一次交换时,它们的温度将连续变化,并且它们都倾向于变得与这个包壳的固定温度相等。
这个作用与热在固体内被传导时所产生的作用完全相同;因为构成这些物体的分子被真空所隔开,并且有受热,积热和发射热的性质。它们每一个都向各处发出辐射线,并且同时从包围它的那些分子那里得到别的辐射线。
45 由位于一个固体物质内部一点所发出的热只能直接通过一段极短的距离;我们可以说,它被最近的粒子所阻截;这些粒子只直接接受这种热,并且作用在更远的点上。气流体则不同;在它们之中,辐射的直接作用在非常远的距离上都是明显的。
46 因此,虽然从一个固体表面的一部分在各个方向上所逃逸的热在空气中传给非常远的点;但是它们仅仅只由这一固体的那些紧靠其表面的分子所发射。一个被加热的物体上处在与把这一物体和外部空间隔开的表面挨得很近的一个点向外部空间发出无数辐射线,但是它们并不能全部都到达那里;它们被减少由这一固体的中间分子所俘获的所有那些热量。实际弥散到空间中去的那部分辐射线,随它们在这一物体内经历的路程更长而变得更少。因此,垂直于这一表面所逃逸的辐射线,其强度比沿斜向离开这同一点的辐射线要大,倾斜得最狠的辐射线则完全被拦截。
同样的结论适用于离表面充分近,可以参与热辐射的所有那些点,由此必然得出,以法向从表面逃逸出的全部热量,比那些斜向逃逸出的要大得多。我们已经使这一问题能够计算,我们的分析证明,辐射线的强度与它们和面元素所成夹角的正弦成正比。实验已经表明一个相类似的结果。
47 这个定理表示一条与热作用的平衡和热作用的方式有必然联系的一般规律。如果从一个受热面所逃逸出的辐射线在所有方向上都有相同的强度,那么,位于由保持一恒温的一个包壳所处处围定的一个空间的某一个这样的点上的一个温度计,将指示比该包壳高得无比的温度 【10】 。正如我们总是注意到的一样,处于这一包壳内的物体不会取得共同的温度;它们所达到的温度或与它们所处的位置有关,或与它们的形状有关,或与相邻物体的形状有关。
如果人们认为在从同一点所逃逸出的辐射线之间有什么不同于我们所阐明的别的联系,那么或者同样的结果会被观察到,或者别的作用同样与一般经验相反。我们已经认识到,这一规律仅仅只是与辐射热平衡的一般事实相一致的规律。
48 如果一个没有空气的空间由一个其各部分都保持共同且不变的温度a的固体所处处围定,并且如果有有效温度a的一个温度计被放在这一空间的任一点上,那么,它的温度将保持不变。因此,它在每一时刻从这个包壳的内表面所得到的热与它向它所发出的热一样多。严格地说,在一给定空间内,热辐射线的这一作用是温度的量度:不过这个考虑预设了辐射热的数学理论。
如果现在在温度计和这个包壳面的一部分之间放进一个其温度是a的物体M,那么温度计将不再得到来自这个内表面的某一部分的射线,但是这些射线将由它从所插入的物体M处所得到的那些射线所补偿。一个简单的计算表明,这个补偿是严格的,因此,温度计的状态将保持不变。若物体M的温度与这个包壳的温度不同,则情况不一样。当它更高时,所插入的物体M向温度计所发出的,并补偿被拦截的射线的这些射线,就传递比前者更多的热;因此,温度计的温度肯定升高。
相反,如果这个插进去的物体的温度比a低,那么温度计的温度肯定下降;因为,这个物体所拦截的射线由它所发出的、即由比包壳的射线更冷的那些射线所代替;因此,温度计就不能完全得到保持其温度a所必需的热。
49 到目前为止我们还没有考虑所有表面都具有反射一部分向它们所发射的射线的能力。如果忽视这个性质,那么我们就只有很不完整的关于辐射热平衡的思想。
这时,假定在保持一恒温的这个包壳的内表面上有一部分在某种程度上具有所说的这种能力;则这个反射面的每一点都将向空间发出两种射线:一种仅仅从组成这一包壳的物质内部发出,其他则仅仅由它们所对着发出的这同一表面所反射。但是,在这个面排斥外部部分入射线的同时,它在内部保留部分它自身的射线。在这一方面,形成一种严格的补偿,也就是说,这个面所阻止发出的它自身的每一条射线,都由一条相同强度的反射线所代替。
如果反射线的这种能力无论在何种程度上对这个包壳的其他部分起作用,或者对被放进这同一空间,并且已经处于共同温度的物体表面起作用,那么,同样的结果就会发生。
因此,热的反射并不干扰温度平衡,并且,当这种平衡存在时,在离开同一点的射线强度据以随发射角的正弦而相应降低的规律中,它不参与任何变化。
50 假定在所有部分都保持温度a的这同一包壳中,我们放进一个孤立物体M和一个抛光金属面R,当金属面R的凹面朝向这一物体时,它就反射它从这一物体所得到的大部分射线;如果我们在物体M和反射面R之间放一个温度计,随物体M的温度或等于,或大于,或小于共同温度a,在这个镜子的焦点上,我们将会观察到三种不同的作用。
在第一种情况下,温度计保持温度a;它得到1°,来自不为物体M和这个镜子所遮挡的这一包壳所有部分的热辐射;2°,由这一物体所发出的射线;3°,面R向焦点所发出的那些射线,或者它们来自这个镜子本身的物质,或者这个镜子表面只反射它们;在最后这种射线中,我们可以区分由物体M向这个镜子所发出的射线和它从这一包壳那里所得到的射线。由假设,所讨论的所有这些射线都由有共同温度a的表面所产生,因此,温度计严格处于同一状态,仿佛由这一包壳所围成的空间不包含任何别的物体,而只含其自身一样。
在第二种情况下,放在已受热物体M和这个镜子之间的温度计肯定获得比a更高的温度。实际上,它得到和在第一种假设中相同的射线;不过有两个明显的差别:第一个差别产生于这样一个事实:由物体M向镜子所发出,并且反射到温度计上的射线,含有比在第一种情况中更多的热。另一个差别取决于这样一个事实:物体M直接向温度计所发出的射线,含有比前面更多的热。这两个原因,主要是第一个,就促使温度计的温度升高。
在第三种情况下,也就是说,当物体M的温度比a低时,温度计也肯定呈现出比a低的温度。事实上,它再次得到我们在第一种情况中所区分的所有各种射线:不过它们之中有两种所含的热比在第一种情况中要少,即,因由物体M发射,而由镜子反射到温度计上的那些射线,和这同一物体M直接向它所发出的那些射线。因此,温度计不能完全得到它为保持它的初始温度a所需要的热。它发出的热比它所得到的热要多。这样必然就是,它的温度肯定会降到它所得到的射线能够补偿它所失去的射线这样一点上。这最后一种作用就是所谓的冷反射(The reflection of cold),严格地说,它在于过弱热反射(The reflection of too feeble heat)。镜子拦截一定的热量,并且用更少的热量代替它。
51 如果在保持恒温a的这个包壳中放进一个物体M,它的温度a′小于a,那么这个物体的存在将使受到它射线作用的温度计降低温度,并且我们可以注意到,从物体M的表面向温度计所发射的射线,一般来说有两种:即来自这一物体M内部的那些射线,来自这一包壳的不同部分、碰到表面M上、然后反射到温度计上的那些射线。后一种射线有共同温度a,但是属于物体M的那些射线包含的热则少一些,这些都是使温度计降温的射线。如果现在改变物体M的表面状态,例如,破坏其光泽,我们就降低了它所具有的反射入射线的能力,温度计的温度就会降得更低,呈现出比a更低的温度a″。事实上,如若不是物体M发出更多的它自己的射线,并且反射更少的它从包壳那里所得到的射线,那么,所有条件就和前一种情况一样;也就是说,有共同温度的最后这些射线,部分地被更冷的射线所代替。因此,温度计就不能再得到和前面一样多的热。
如果与物体M的表面变化无关,我们放进一个适合于把离开M的射线反射到温度计上的金属镜,那么温度将呈现出比a″更小的值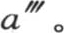 事实上,这个镜子从温度计那里拦截都有温度a的这个包壳的部分射线,并且用三种射线取而代之;即1°,来自这个镜子内部本身,并且有相同温度的那些射线;2°,这个包壳的不同部分以相同温度向镜子所发出,并且被反射到焦点上的那些射线;3°,来自物体M内部,落到镜子上、然后被反射到温度计上的那些射线。最后这种射线的温度比a低;因此温度计不能再得到和它在放进镜子之前所得到的一样多的热。
事实上,这个镜子从温度计那里拦截都有温度a的这个包壳的部分射线,并且用三种射线取而代之;即1°,来自这个镜子内部本身,并且有相同温度的那些射线;2°,这个包壳的不同部分以相同温度向镜子所发出,并且被反射到焦点上的那些射线;3°,来自物体M内部,落到镜子上、然后被反射到温度计上的那些射线。最后这种射线的温度比a低;因此温度计不能再得到和它在放进镜子之前所得到的一样多的热。
最后,如果我们还着手改变镜子的表面状态,通过对它进行更理想的抛光,增加它反射热的能力,那么温度计的温度还会降得更低。事实上,在前面的情况中所出现的所有条件都存在。所发生的只是,镜子更少发出它自己的射线,并且用它所反射的那些射线来代替它们。现在,在最后这些射线中,所有那些从物体M内部所发出的射线的强度都比以前曾从金属镜内部所发出的射线小;因此,温度计所得到的热仍然比前面情况中的更少;因此,它将呈现出比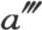 更低的温度
更低的温度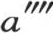 。
。
运用同样这些原理,我们很容易解释热辐射和冷辐射的所有已知事实。
52 决不能把热效应与那些分子处于静止状态的弹性流体的效应相提并论。
试图从这个假设推出我们在本书中已解释的、所有实验已确证的这一传导规律,是徒劳的。热的自由态和光的自由态一样;而这种元素的激活态完全不同于气态物质的激活态。热以同一方式在真空,在弹性流体,以及在液体和固体物质中起作用,它仅仅以辐射的方式传导,不过它的显效应(sensible effects)随物体性质而异。
53 热是一切弹性的源泉;它是保持固体物质的形状和液体体积的斥力。在固体物质中,如果相邻分子的相互吸引作用不为分离它们的热所破坏,那么它们就会产生这种作用。
这种弹力随温度更高而更大;这就是为什么物体在它们的温度升高或降低时就膨胀或收缩的原因。
54 在固体物质内部,热的斥力和分子的引力之间所存在的平衡是稳定的;也就是说,当受到偶然原因干扰时,它就重建它自己的平衡。如果分子被安排在适合于平衡的距离上,并且如果一外力开始增加这一距离而不引起任何温度变化,那么,经过无数次变得愈来愈不明显的振荡之后,引力的作用就开始超过热的作用,并使分子恢复到它们的初始位置。
当一个机械原因使这些分子的初始距离缩小时,就会在相反的意义上产生一种类似的作用;诸如此类的有发出宏亮的声音的物体和柔性物体的振动基点,以及它们所有的弹性作用的振动基点等等。
55 在物质的液态和气态中,外压力是附加到或补充到分子引力上的,并且,作用在外表面时,它们并不抗形变,而只仅仅抗所占据的体积的变化。分析的研究将最恰当地表明抗分子引力或抗外压力的热的斥力怎样参与由一种或多种元素所组成的物体的,固体的或者是液体的合成,怎样决定气流体的弹性;不过,在我们之前,这些研究不属于这一主题,它们出现在动力学理论中。
56 毫无疑问,和光的作用方式一样,热的作用方式总是在于射线的相互传递,并且这一解释在现在已为大多数物理学家所接受;但是,建立热的理论并不需要考虑属于这一方面的现象。在本书中,读者将会看到,作为普通观察的必然结论,在固体或液体物质中,辐射热的平衡与传导怎样独立于任何物理解释而得到严格的论证。
第三节 热传导原理
57 我们现在开始考察实验所教给我们的关于热传导的知识
如果两个相同的分子由相同的物质所组成,并且有相同的温度,那么它们每一个都从另一个那里得到和它向它所发出的一样多的热;这样,它们的相互作用就可以看做为0,因为这种作用的结果不会引起这些分子状态的任何变化。相反,如果第一个比第二个热,那么它向它发出比它从它那里所得到的更多的热;这种相互作用的结果就是这两热量的差。就所有情况而言,我们排除任一对质点相互发出两相等热量这样一种情况。我们设想,只是受热较多的一点作用在另一点上,并且由于这一作用,第一个质点失去由第二个质点所得到的一定的热量。因此,这两个分子的作用,或者最热的分子传递给另一个的热量,就是它们相互发出的两热量的差。
58 假定我们在空气中放一个同质固体,它的不同点有不同的有效温度,则组成这一物体的每一个分子开始都会或者从距离极近的那些分子那里得到热,或者传热给它们。在同一时刻在这一物体的所有点之间所发生的这一作用,会在所有温度中产生一个无穷小的合变化(resultant change):这一固体将在每一时刻受到相似的作用,因此,温度的变化会变得愈来愈明显。
只考虑两个相等且挨得极近的分子m和n的系统,让我们来确定在某一时刻内第一个分子从第二个分子那里所能得到的热量:这样我们就可以把这同样的推理应用到与点m充分近、在第一个时刻内直接作用于它的所有其他点上。
由点n传递给点m的热量取决于这一时刻的长短,取决于这两点之间的这个很短的距离,取决于这两个点的有效温度,并且取决于这一固态物体的质;也就是说,如果这些因素中的某一个发生变化,即使所有其他因素都保持不变,所传导的热仍然会发生变化。目前,实验在这一方面已经揭示出一个一般的结果:它在于,所有其他环境保持不变,这两个分子中的一个从另一个那里所得到的热量,与这两个分子的温差成正比。因此,如果一切其他条件保持不变,点n与点m的温差变成二倍、三倍或四倍的,那么这一热量也是二倍、三倍或四倍的。为了解释这一结果,我们应当认为,n对m作用的大小正好与这两点间温差的大小一样:如果温度相等,这个作用就等于0,但是如果分子n比同样的分子m含有更多的热,也就是说,如果m的温度为v,n的温度就是v+∆,那么,一部分超出热就从n传到m。现在如果热的这个超出量是两倍的,或者,与之等价,如果n的温度是v+2∆,那么,超出热就由两个相等部分所构成,这两部分对应于整个温差的两等分;这两部分的每一部分都有它固有的作用,就好像是单独存在一样:因此,由n所传递给m的热量就和在温差只是∆时所传递的热量的两倍一样多。超出热的这两个不同部分的同时作用,就是构成热传导原理的作用。由此得出:部分作用的和,或者m从n那里所得到的总热量,与这两温度的差成正比。
59 用v和v′表示两个相同分子m和n的温度,用p表示它们的极短距离,用dt表示这一时刻的无穷小长度,那么,m在这一时刻内从n那里所得到的热量就由(v′-v)φ(p)·dt来表示。我们用φ(p)表示距离p的某个函数,在固体和在液体中,当p有一个显著的量时,函数φ(p)就变成0。这个函数对同一给定物体的每一点都是相同的;它随这一物体的质而变化。
60 物体通过它们表面所失去的热量服从于这同一条原理。如果我们用σ表示其所有点都有温度v的这个表面的有限的或无穷小的面积,并且如果a表示大气温度,由于系数h是外热导率的量度,所以我们就可以把σh(v-a)dt作为这个面σ在时刻dt内所传送到空气中去的热量表达式。
当其中一个传给另一个一定热量的这两个分子属于同一固体时,所传导的热的精确表达式就是我们在前一目中所给出的公式;并且,由于这两个分子挨得极近,所以温差极小。当热从一个固体传到一种气态介质中去时,情况就不同了。然而实验使我们认识到,如果这个差是一个充分小的量,那么所传送的热就显然与那个差成正比,并且,在开始的这些研究中 【11】 ,可以把数h看做为这一表面的每一状态所特有的、且与温度无关的、有一个不变值的数。
61 这些与所传导的热量有关的命题已经从不同的观察中导出。作为所讨论的这些表述的一个明显推论,我们首先看到,如果我们用一个共同的量使这一固态物体和它被置于其中的介质的所有温度升高,那么,温度的连续变化就完全相同,如同不曾使初始温度升高一样。现在,这个结果明显地与实验一致;它已经得到首批观察过热作用的物理学家们的承认。
62 如果这一介质保持在一恒温上,并且,如果被放到这一介质中的受热物体的体积充分小,以便在温度愈来愈低时能使这个物体所有点的温度都明显相同,那么,从同样这些命题可以得出,在每一时刻过这一物体表面所逃逸的热量与它的有效温度超过其介质温度的超出量成正比。因此,正如在本书中将会看到的,我们不难得出结论,其横坐标表示历经时间,纵坐标表示对应于那些时间的温度的这条曲线是一条对数曲线:现在,当这个固体的温度超过其介质温度的超出量是一个充分小量时,观察也提供同样的结果。
63 假定这一介质保持恒温0度,这同一物质的不同点a,b,c,d,…的初始温度是α,β,γ,δ,…,在第一时刻结束时它们变成α′,β′,γ′,δ′,…,在第二时刻结束时它们变成α″,β″,γ″,δ″,…,如此类推。根据所阐明的这些命题我们不难得出结论,如果同样这些点的初始温度是gα,gβ,gγ,gδ,…,(g是一个任意数),那么,由于不同点的作用,在第一时刻结束时,它们就变成gα′,gβ′,gγ′,gδ′,…,在第二时刻结束时,它们就变成gα″,gβ″,gγ″,gδ″,…,如此类推。例如,让我们来比较当这些点a,b,c,d,…的初始温度是α,β,γ,δ等等时的情况和当它们的初始温度是2α,2β,2γ,2δ,…时的情况,介质在这两种情况中保持0度。在第二个假定中,任意两点的温差是第一个假定中的两倍,每一点的温度超过介质的每一分子的温度的超出量也是两倍;因此在第二个假定中,任一分子向别的任一分子所发出的热量,或者它所得到的热量,是它若在第一个假定中所发出或者是得到的两倍。由于每一点所经历的温度变化与所得到的热量成正比,由此得出,在第二种情况中,这一变化是它在第一种情况中的两倍。现在我们已经假定,第一点的初始温度为a,它在第一时刻结束时变成a′;因此,如果这一初始温度原本是2a,并且如果所有其他温度都翻一倍,那么它就变成2a′。所有其他分子b,c,d的情况亦如此,并且,如果这个比不是2,而是任一数g,也可以得出类似的结果。这样,从热传导原理得出:如果我们以任一给定的比升高或者是降低所有的初始温度,那么,我们就以同样的比升高或者是降低所有的后续温度。
同前面两个结果一样,这个结果由观察所确证。如若从一个分子传给另一个分子的热量实际上不与温差成正比,那么这个结果就不成立。
64 关于一根金属棒或一个金属环的不同点的永恒温度,以及关于相同物体中和形如球和立方体的几个其他固体中的热传导,我们已经以精密的仪器作了观察。这些实验结果与从前面的例题所导出的结果是一致的。如果从一个固体分子传送到另一个固体分子,或传送到一个空气分子的热量不与温度的超出量成正比,那么它们就会完全不同。首先有必要弄清这一命题的所有严格结论;由此我们确定作为这一问题的目的的那些量的主要部分。这样,通过比较计算值和那些由许多非常精确的实验所给出的值,我们就很容易测量系数的变化,并完善我们第一阶段的研究。
第四节 均匀热运动和线性热运动
65 首先,我们将在最简单的情况中,即在围在两个平行平面之间的一个无穷固体的情况中,考虑均匀的热运动。
我们假定由某种同质物质所组成的一个固体被围在两个无穷平行平面之间;下平面A以任一原因保持恒温a;例如,我们可以设想这一物体被延展,并且平面A是这一固体和这种围住它的物质所共有的一个截面,并且由一个恒定热源加热其所有的点;上平面B也由一个类似原因保持一固定温度b,其值小于a值;问题是要确定,如果它持续无穷时间,那么这一假定的结果会是怎样的。
如果我们假定,这一物体所有部分的初始温度是b,那么显然,离开热源A的热将传得愈来愈远,并且会提高围在这两个平面之间的分子的温度;然而根据假定,由于上平面的温度不能升高得超过b,所以热将在更冷的物质中弥散,通过与这种冷物质接触,使平面B保持恒温b。这一温度系统愈来愈趋近于一个终极状态,这一状态永远不能达到,但是,正如我们将要表明的,只要它一旦形成,它就具有存在和保持自身无变化的性质。
在我们要考虑的这个终极和固定状态中,这一固体的一点的永恒温度显然与平行于基底的同一截面的所有点相同;我们要证明,为一个中间截面的所有点都共有的这一固定温度,以算术级数从基底向上平面递减,也就是说,如果我们用垂直于两个平面之间的距离AB所作的纵坐标Aα和Bβ表示两恒温a和b(见图1),那么中间薄层的固定温度就由连结端点α和β的直线αβ的纵坐标来表示,因此,如果用z表示一个中间截面的高度,或表示它与平面A的垂直距离,用e表示整个高度或距离AB,用v表示其高为z的截面温度,那么,我们肯定有方程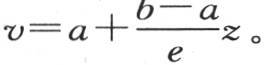
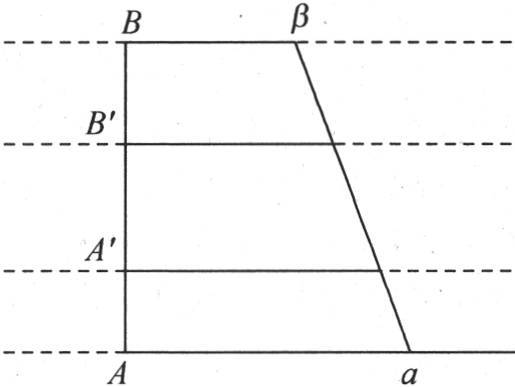
图1
事实上,如果这些温度最初是根据这一规律而形成的,那么,在这一固体的状态中就不会发生任何变化。为了使我们自己确信这一点,只要比较一个中间截面A′所通过的热量和在同一时刻内另一截面B′所通过的热量就够了。
考虑到这一固体的终极状态已经形成并延续,我们看到,这一物体在平面A′以下的这部分肯定向这一平面之上的那部分传热,因为第二部分比第一部分冷。
设想这一固体的两点m和m′,它们相互挨得很近,并且,为使它们在一个无穷小时刻内发生作用,我们以任一方式使其中一个m位于平面A′的下方,另一个m′位于这个平面的上方:较热的点m将经过平面A′向m′传递一定的热量。设x,y,z是点m的直角坐标,x′,y′,z′是点m′的坐标;同样设另外两点n和n′,它们相互挨得很近,并且它们相对于平面B′所处的位置与m和m′相对于平面A′所处的位置相同:也就是说,当用ξ表示两截面A′和B′的垂直距离时,点n的坐标就是x,y,z+ξ,点n′的坐标就是x′,y′,z′+ξ;这两个距离mm′和nn′相等:并且,点m的温度v超过点m′的温度v′的差与两点n和n′的温差相等。事实上,前一个差可以这样来确定:在一般方程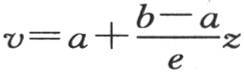 中,先代入z,然后代入z′,并用第一个方程减去第二个方程,因此,这一结果
中,先代入z,然后代入z′,并用第一个方程减去第二个方程,因此,这一结果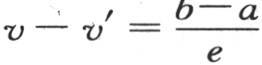
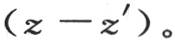 通过z+ξ和z′+ξ的代换,我们会发现,点n的温度超过点n′的温度的超出量,也由
通过z+ξ和z′+ξ的代换,我们会发现,点n的温度超过点n′的温度的超出量,也由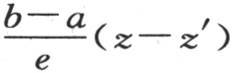 来表示。
来表示。
由此得出,点m向点m′所发出的热量与点n向点n′所发出的热量相等,因为,在确定所传递的热的这个量时,同时起作用的所有这些因素都是相同的。
显然,我们可以把同样的推理应用到经过截面A′或者截面B′而相互传热的每一个两分子系统中去;因此,如果我们能够计算同一时刻内经过截面A′或者截面B′所流过的总热量,我们就会发现,对于这两个截面来说,这个量是相等的。
由此得出,这一固体在A′和B′之间的这一部分总是得到和它所失去的一样多的热,由于这一结果可应用于包含在两个平行截面之间的这一物体的任一部分,所以,显然这一固体的任一部分都不能达到比它目前所处的更高的温度。因此,我们就严格论证了,这一棱柱的状态,正好和它开始时一样,将继续存在。
因此,围在两个无穷平行平面之间的一个固体的不同截面的永恒温度,由一条直线αβ的纵坐标表示,并且满足线性方程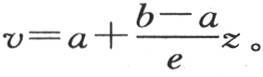
66 如上所述,我们清楚地看到什么因素构成在由两个无穷平行平面所围成的固体中的热传导,这两个平面的每一个都保持一恒温。热经下平面逐渐贯穿到这一物质中去:中间截面的温度被升高,但是,它们决不能超过,甚至也不能完全达到它们愈来愈接近的某个极限:这个极限温度和终极温度对不同的中间薄层来说是不同的,并且以算术级数从下平面的固定温度降至上平面的固定温度。
这种终极温度是为使固体的状态达到永恒而不得不给予固体的那些温度;正如我们即将看到的一样,在它之前的变化状态也服从于分析:不过,我们现在只考虑终极温度或永恒温度系统。在这种最后的状态中,在每一时间间隔内,过一个平行于基底的截面或者是过那个截面的一个确定部分,有一定的热量流过,如果时间间隔相等,则这个量不变。这种均匀流动对于所有中间截面都是相同的;它与从热源所发出的热量相等,并且,根据保持温度不变这一原因,它与在同一时间内从这一固体的上表面所失掉的热量也相等。
67 现在的问题是要测量在一给定时间内,在这一固体中过平行于基底的某一个截面的一个确定部分所均匀传导的热量:正如我们将看到的一样,它取决于两极端温度a和b,取决于固体两边之间的距离e;如果这几个因素中的任何一个开始发生变化,其他因素保持不变,它都会发生变化。假定第二个固体由和第一个固体一样的同一种物质组成,并且被包围在两个无穷平行平面之间,这两个平面的垂直距离是e′(见图2):下边保持固定温度a′,上边保持温度b′;两个固体都被看做是处于具有一旦形成便保持自身不变的性质的终极状态和永恒状态中。因此,对于第一个固体来说,温度规律由方程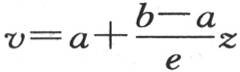 表示,第二个固体,则由方程
表示,第二个固体,则由方程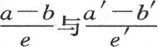 表示,第一个固体中的v和第二个固体中的u是其高为z的截面温度。
表示,第一个固体中的v和第二个固体中的u是其高为z的截面温度。
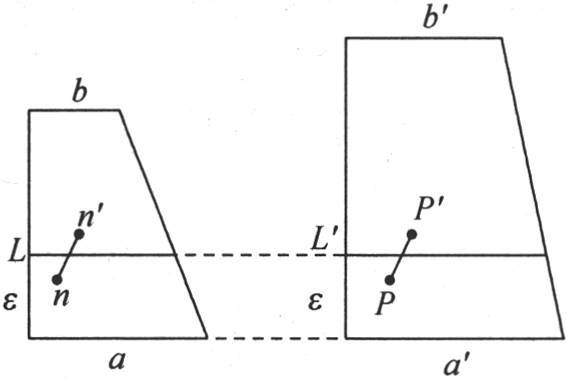
图2
如此,我们将比较在单位时间内过第一个固体的一个中间截面L上的单位面积的热量和在同一时间内过第二个固体的一个截面L′上的相同面积的热量,ε是两个截面的共同高度。就是说,是它们每一个到它们自己基底的距离。我们将在第一个物体中考虑两个很近的点n和n′,其中一点n在平面L下面,另一点n′在这个平面上面:x,y,z是n的坐标,x′,y′,z′是n′的坐标,ε小于z′大于z。
我们在第二个固体中也考虑两点p和p′的瞬时作用,这两点相对于截面L′所处的位置与点n和n′相对于第一个固体的截面L所处的位置相同。因此,在第二个固体中用以表示三直交轴的这同样的坐标x,y,z和x′,y′z′,也确定点p和p′的位置。
现在,点n到点n′的距离与点p到p′的距离相等,并且,由于这两个物体由同一种物质所组成,所以,根据热传导原理我们得出结论,n对n′的作用,或者n所给予n′的热量,以及p对p′的作用,彼此之间的比与温差v-v′和u-u′的比相同。
这样,在属于第一个固体的方程中先代入v,然后代入v′,并相减,我们就有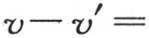
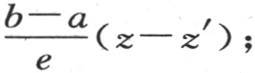 通过第二个方程,我们同样有
通过第二个方程,我们同样有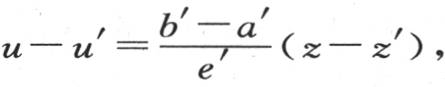 因此,所考虑的这两个作用的比就是
因此,所考虑的这两个作用的比就是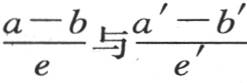 的比。
的比。
现在我们可以设想许多其他的两分子系统,它们中的第一个分子过平面L向第二个分子发出一定的热量,在第一个固体中所选出的每一个这样的系统都可以与位于第二个固体中的对应系统相比较,这个对应系统过截面L′而发生作用;这样,我们可以再次应用前面的推理来证明这两个作用的比总是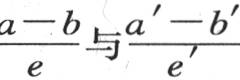 的比。
的比。
于是,在某一时刻内过截面L的总热量,就由其每一个都由两点所组成的无数系统的同时作用所产生;因此,这一热量和在第二个固体中在同一时刻过截面L′的总热量的相互之间的比,也是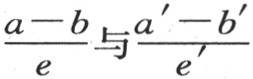 的比。
的比。
这样,我们就容易相互比较这两个固体中所均匀传导的恒定热流量的强度,即在单位时间内,过这两个固体的每一个的单位面积的热量。这两个强度的比是两个商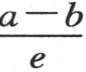 和
和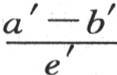 的比。如果这两个商相等,那么,在其他方面,无论a,b,e,a′,b′,e′会取什么值,这两个热流量就相等;一般地,用F表示第一个热流量,用F′表示第二个热流量,我们则有
的比。如果这两个商相等,那么,在其他方面,无论a,b,e,a′,b′,e′会取什么值,这两个热流量就相等;一般地,用F表示第一个热流量,用F′表示第二个热流量,我们则有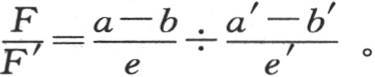
68 假定在第二个固体中,下平面的永恒温度a′是沸水温度1;上平面的这种温度b′是溶冰温度0;两个平面的距离e′是测量单位(1米);如果这一固体由一种已知的物质所组成,那么,让我们用K来表示在单位时间内(1分钟)经过这一固体中单位面积的恒定热流量;K表示一定数量的热量单位,即把1千克冰转化成水所需要的热的一定数量的倍数;一般地,在由相同物质所组成的一个固体中,我们用方程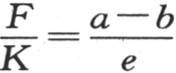 或
或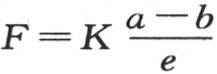 来确定恒定热流量F。
来确定恒定热流量F。
F值表示在一个单位时间内经过平行于基底的截面上的单位面积的热量。
因此,温度计所测得的、由其垂直距离为e、并保持固定温度a和b的两个平行且无穷的平面所围成的固体的状态,由两个方程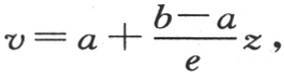 和
和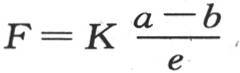 或者
或者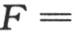
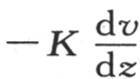 来表示。
来表示。
这两个方程的第一个表示温度从下边降到上边所遵循的规律,第二个指明在一给定时间内经过平行于基底的某一截面的一个确定部分的热量。
69 我们把参与第二个方程的系数K看做是每种物质的热导率的量度;这个数对于不同的物体有非常不同的值。
一般地,它在包围在两个无穷平行平面之间并且由一种已知物质所组成的同质固体中,表示在一分钟内,在平行于这两个极面的一个截面上,过一平方米的面积所流过的热量,同时假定这两个极面一个保持沸水温度,另一个保持溶水温度,并且假定所有中间平面都达到并保持一永恒温度。
我们可以应用另一个热导率的定义,因为,我们可以用把热容量看做是指单位体积而不是指单位物质的方法来计算热容量。所有这些定义,只要它们是清晰和精确的,就同样都是好的。
我们马上要指出怎样通过观察来确定不同物质中的热导率或者是热导性(The con ducibility or conductibility)的K值。
70 要建立我们在第68目中所提到的方程,并不一定要假定发挥其作用的这些点是在极短距离中经过这些平面的。
如果这些点的距离有任一数量,其结果仍然一样;因此,它们也可以应用到在构成这一假定的其他条件都保持相同时热的直接作用在这一物体内部延伸到相当远的距离的情况中去。
我们只需假定,保持固体表面温度的原因,不仅仅对极靠近这一表面的那一部分物质起作用,而且它的作用也延伸到一个有限深度。在这种情况中,方程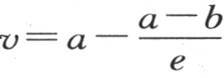 仍然表示固体的永恒温度。这一命题的真正意义是:如果我们对这一物质的所有点都给出由这个方程所表示的温度,并且,如果除开任何原因之外,对这两个极端薄层的作用,总是使它们的每一个分子都保持在这同一个方程对它们所规定的温度上,那么,这一固体的内点将保持它们的初始状态而无任何变化。
仍然表示固体的永恒温度。这一命题的真正意义是:如果我们对这一物质的所有点都给出由这个方程所表示的温度,并且,如果除开任何原因之外,对这两个极端薄层的作用,总是使它们的每一个分子都保持在这同一个方程对它们所规定的温度上,那么,这一固体的内点将保持它们的初始状态而无任何变化。
如果我们假定这一物体一点的作用可以延伸一个有限的距离ε,那么必然地,由外因保持其状态的这两个极端薄层的厚度,就应该至少等于ε。不过事实上,在固体的自然状态中,当量ε仅仅只有一个微不足道的值时,我们就可以不考虑这一厚度;并且它仍然满足这一外因对包围这一固体的这两个极薄薄层的作用。这就是我们始终应当由这一表述所理解的保持表面温度不变的含意。
71 我们继而进一步考察这同一个固体在它的一个极面受保持一种恒温空气的作用时的情况。
假定下平面无论以何种外因保持固定温度a,并且上平面不像以前那样保持较低温度b,而是受保持那种较低温度b的空气的作用,两个平面的垂直距离仍用e来表示:问题是要确定终极温度。
假定在这一固体的初始状态中,它的分子的共同温度是b或者小于b,我们不难设想,从热源A所不停地发出的热贯穿到这一物体中,并且愈来愈提高中间截面的温度;上表面逐渐被加热,它允许已经贯穿到这一固体中的一部分热逃逸到空气中去。这一温度系统不断接近一个终极状态,这一状态一旦形成,就会保持不变;在这个我们要考察的终极状态中,平面B的温度有一个固定的但却是待定的值,我们用β来表示它,并且,由于下平面A也保持一永恒温度a,所以这一温度系统由一般方程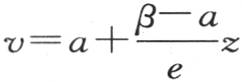 来表示,v仍然表示其高为z的截面的固定温度。在单位时间内,过任一截面的单位面积的热量,都是
来表示,v仍然表示其高为z的截面的固定温度。在单位时间内,过任一截面的单位面积的热量,都是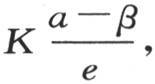 K表示内热导率。
K表示内热导率。
我们现在应当考虑到:其温度为β的上表面B允许一定的热量逃逸到空气中去,这个量肯定严格等于经过这个固体任一截面L的热量。如若不然,则包含在这一截面L和平面B之间的这一部分物质就不能得到等于它所失去的热量;因此,它就不能保持它的状态,这与假设相反;因此,在这个表面上的恒定热流量等于经过这一固体的热流量。现在,在单位时间内从平面B的单位面积所逃逸的热量由h(β-b)来表示,b是空气的固定温度,h是表面B的热导率的量度;因此,我们肯定有方程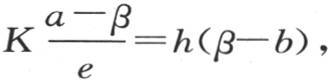 它确定β的值。
它确定β的值。
由此可以推出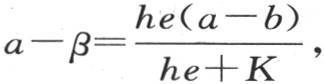 这个方程的右边是已知的;因为温度a和b被给定,量h,K,e同样被给定。
这个方程的右边是已知的;因为温度a和b被给定,量h,K,e同样被给定。
为了表示这个固体任一个截面的温度,当把a-β这个值代到一般方程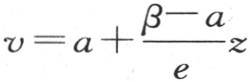 中去时,我们就有方程
中去时,我们就有方程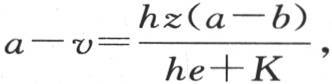 随相应变量v和z而进入这一方程的,只有一些已知量。
随相应变量v和z而进入这一方程的,只有一些已知量。
72 到此,我们就确定了包围在保持不等温的两个无穷平行平面之间的固体温度的终极和永恒的状态。严格地说,这第一种情况就是热的线性传导和均匀传导的情况,因为在与这一固体的边平行的平面上没有热传导;由于这个热流量的值对于所有时刻和所有截面来说都相等,所以,传给这一固体的热是均匀流动的。
我们现在要重新表述从这个问题的考察中所得出的三个主要命题;这三个命题可以应用于许多地方,并且构成我们的理论的最基本的原理。
第一,如果在这个固体厚度为e的两极,我们作表示这两个边的温度a和b的垂线,并且,如果我们引连结这两个初始纵坐标端点的直线,那么,所有中间温度就都与这条直线的纵坐标成正比;它们由一般方程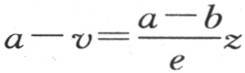 来表示,v表示其高为z的截面温度。
来表示,v表示其高为z的截面温度。
第二,由于其他一切条件都相同,所以,在单位时间内,在平行于两个极面的任一截面上的单位面积内所流过的热量与极端温度的差a-b成正比,与分离这两个面的距离e成反比。这个热量由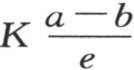 来表示,或者,如果我们从这个一般方程推出恒定值
来表示,或者,如果我们从这个一般方程推出恒定值 则由
则由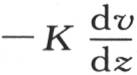 表示;对于一种已知的物质,在所考察的这一固体中,这个均匀热流量总可以由垂线e和其纵坐标表示温度的这条直线之间的夹角的正切来表示。
表示;对于一种已知的物质,在所考察的这一固体中,这个均匀热流量总可以由垂线e和其纵坐标表示温度的这条直线之间的夹角的正切来表示。
第三,由于这个固体的两个极面中的一个始终受温度a的作用,所以,如果另一个极面受保持固定温度b的空气的作用;那么,同前一种情况一样,与空气接触的这个面就达到一固定温度β,它大于b,并且这个面允许一热量在单位时间内过一个单位面积逃逸到空气中去,这个量由h(β-b)来表示,h表示这个面的外热导率。
这同一热流量h(β-b)与过这一棱柱、其值为K(a-β)的热流量相等;因此,我们有方程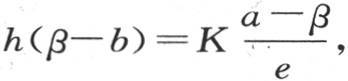 它给出β的值。
它给出β的值。
第五节 细棱柱中永恒温度的规律
73 我们很容易把刚才所解释的原理应用到下述问题中去,这个问题本身很简单,但是把它的解建立在精确理论之上,却是一个重要问题。
形如无穷长的长方体的一个金属棒受一个热源的作用,这个热源使它末端A的所有点都产生一恒温。我们需要确定这根棒的不同截面的固定温度。
假定垂直于轴的截面是一个正方形,这个正方形的边2l非常小,以至于我们可以认为同一个截面上不同点的温度相等而不会有明显的误差。金属棒周围的空气保持恒温0度,并且以匀速气流流动。
在这个固体内部,热将陆续经过位于热源右边 【12】 的所有部分,并且不直接受它的作用;它们将愈来愈被加热,但是每一点的温度不会升得超过某个极限。这个最高温度对于每一个截面都是不同的;一般地,它随截面到原点距离的增加而下降:我们用v表示垂直于轴并且与原点A的距离为x的截面的固定温度。
在这固体的每一点都达到它的最高热度之前,温度系统将不断变化,并且愈来愈接近于一个固定状态,这个状态就是我们所要考察的状态。这个终极状态一旦形成,它就保持自身不变。为了使温度系统成为永恒的,在单位时间内,经过一个与原点距离为x的截面的热量,就应当与在同一时间内,经过位于这同一截面右边的那一部分棱柱外表面所逃逸的所有热量完全平衡。其厚为dx,其外面积为8ldx的薄层,在单位时间内,允许逃逸到空气中去的热量,用8hlv·dx来表示,h是棱柱外热导率的量度。因此,取从x=0到x=∞的积分∫8hlv·dx,我们就得到在单位时间内从这根棒的整个表面所逃逸的热量;如果我们取从x=0到x=x的相同积分,我们就得到经过包含在热源和距离为x的截面之间的那部分面积所失去的热量。用C表示其值不变的第一个积分,用∫8hlv·dx表示第二个积分的变化值,差C-∫8hlv·dx就表示经过这一截面右边的那部分表面所逃逸到空气中去的全部热量。另一方面,包围在距离为x和x+dx的两个无穷近的截面之间的这个固体的薄层,肯定类似于一个无穷固体,这个无穷固体由两个平行平面所界定,这两个平行平面有固定温度v+dv,因为由假定,这个温度在这同一截面的整个范围中不发生变化。这个固体的厚是dx,这个截面面积是4l2 :因此,由前面的原理,在单位时间内,经过这个固体的一个截面所均匀流过的热量,是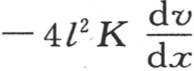 【13】 ,k是内热导率:因此,我们肯定有方程
【13】 ,k是内热导率:因此,我们肯定有方程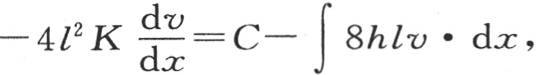 即
即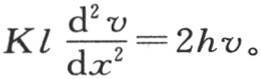
74 通过考虑包围在距离为x和x+dx的两个截面之间的一个无穷薄薄层中的热平衡,我们会得到同样的结果。事实上,在单位时间内,经过位于距离为x的第一个截面的热量,是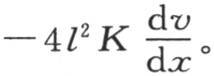 为了得出在同一时间内经过位于距离为x+dx的第二个截面所流过的热量,我们应当在上面的式子中把x变成x+dx;结果得到
为了得出在同一时间内经过位于距离为x+dx的第二个截面所流过的热量,我们应当在上面的式子中把x变成x+dx;结果得到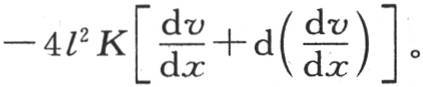 如果我们从第一个式子中减去第二个式子,我们就求出由这两个截面所围成的这一薄层在单位时间内得到多少热量;并且,由于这一薄层的状态是永恒的,所以由此可见,所获得的全部热量经过这同一薄层的外表面8ldx而被耗散到空气中去;既然最后的热量是8hlvdx:因此,我们得到同样的方程
如果我们从第一个式子中减去第二个式子,我们就求出由这两个截面所围成的这一薄层在单位时间内得到多少热量;并且,由于这一薄层的状态是永恒的,所以由此可见,所获得的全部热量经过这同一薄层的外表面8ldx而被耗散到空气中去;既然最后的热量是8hlvdx:因此,我们得到同样的方程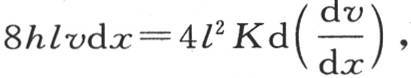 从而
从而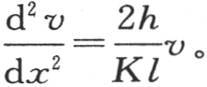
75 这个方程无论以什么方式组成,我们都有必要注意,进入其厚为dx的这个薄层的热量都有一个有限值,它的精确表达式是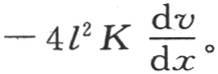 由于这个薄层包围在两个表面之间,其中第一个有温度v,第二个有较低温度v′,所以我们看到,它通过第一个面所得到的热量依赖于差v-v′,并且与它成正比,但是,这个注记还不足以完成这个计算。所讨论的这个量不是一个微分:它有一个有限值,因为它等价于经过位于这个截面右边这一棱柱的那部分表面所逃逸的全部热量。为了形成一个关于它的精确思想,我们应当比较其厚为dx的薄层和由其距离为e、并且保持不相等的温度a和b的两个平行平面所限定的固体。经过较热的面而进入这样一个棱柱的热量事实上与极端温度的差a-b成正比,但是它不仅仅依赖于这个差:由于所有其他条件相同,所以当棱柱愈厚时,它就愈少,一般地,它与
由于这个薄层包围在两个表面之间,其中第一个有温度v,第二个有较低温度v′,所以我们看到,它通过第一个面所得到的热量依赖于差v-v′,并且与它成正比,但是,这个注记还不足以完成这个计算。所讨论的这个量不是一个微分:它有一个有限值,因为它等价于经过位于这个截面右边这一棱柱的那部分表面所逃逸的全部热量。为了形成一个关于它的精确思想,我们应当比较其厚为dx的薄层和由其距离为e、并且保持不相等的温度a和b的两个平行平面所限定的固体。经过较热的面而进入这样一个棱柱的热量事实上与极端温度的差a-b成正比,但是它不仅仅依赖于这个差:由于所有其他条件相同,所以当棱柱愈厚时,它就愈少,一般地,它与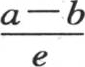 成正比。这就是为什么经过第一个面而进入这个其厚为dx的薄层的热量与
成正比。这就是为什么经过第一个面而进入这个其厚为dx的薄层的热量与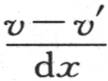 成正比的原因。
成正比的原因。
我们强调这个注记,因为忽视它是建立这一理论的第一个障碍。如果我们不对这个问题的基础作彻底的分析,那么我们得到的方程就不是齐次的,更何况就不能建立表示更复杂的情况的热运动方程了。
为了使我们不至于把观察在特殊情况下所提供的结论看做是一般的,还必需在这个计算中考虑棱柱的大小。这样,通过实验我们发现,一端受热的一根铁棒,在与热源距离6英尺处,不能得到1度的温度(80进制温标 【14】 );因为要产生这一作用,热源的热就必须大大超过铁的溶点;不过这个结果依赖于所使用的这个棱柱的粗细。如果它愈粗,那么热就被传导到愈远的距离,也就是说,由于所有条件都保持不变,所以当这根棒愈粗时,它达到1度的固定温度的那个点就离热源愈远。通过加热一根铁棒的一端,我们总可以在这一固体的另一端升高1度的温度;我们只需使它的基底半径充分大就行了:我们可以说,这是显然的,此外,读者可在这个问题的解中找到一个证明(第78目)。
76 【15】 上述方程的积分是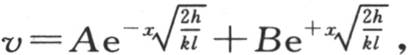 A和B是两个任意常数;现在,如果我们假定距离x是无穷的,那么温度值v就肯定无穷地小;因此,项
A和B是两个任意常数;现在,如果我们假定距离x是无穷的,那么温度值v就肯定无穷地小;因此,项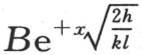 在积分中就没有了:这样,方程
在积分中就没有了:这样,方程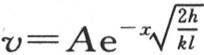 就表示这个固体的永恒状态;在原点的温度由常数A所表示,因为那是当x为0时的v值。
就表示这个固体的永恒状态;在原点的温度由常数A所表示,因为那是当x为0时的v值。
温度下降所遵循的这个规律和实验所给出的规律相同;有几个物理学家已经观察过一根金属棒的一端受一热源的恒定作用时这根金属棒在不同点的固定温度,并且他们已经确定,与原点的距离表示对数,温度表示相应的数。
77 * 由于两相邻温度的恒商的数值由观察所确定,所以我们容易推出比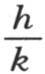 的值;因为,用v1 ,v2 表示对应于距离x1 ,x2 的温度,我们有
的值;因为,用v1 ,v2 表示对应于距离x1 ,x2 的温度,我们有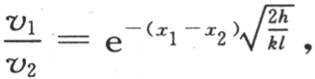 因此,
因此,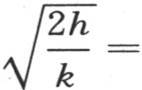
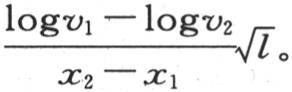
至于h和k这两个独立的值,它们不能由这种实验来确定:我们还应当观察变化的热运动。
78 【16】 假定相同物质不同粗细的两根棒在它们的端点受到相同温度A的作用;设l1 是第一根棒的某一个截面的边,l2 是第二根棒的某一个截面的边,为了表示这两个固体的温度,我们有方程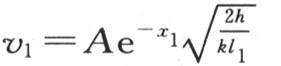 和
和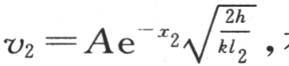 在第一个固体中,v1 表示由距离x1 所给出的一个截面的温度,在第二个固体中,v2 表示由距离x2 所给出的截面温度。
在第一个固体中,v1 表示由距离x1 所给出的一个截面的温度,在第二个固体中,v2 表示由距离x2 所给出的截面温度。
当这两根棒达到一个固定状态时,第一根棒离热源一定距离的截面温度与第二根棒离热源相同距离的截面温度是不等的;为了使这两个固体的温度相等,距离应当是不同的。如果我们想相互比较从原点到这两根棒达到相同温度的点的距离x1 和x2 ,我们就应当使这两个方程的右边相等,由此我们得出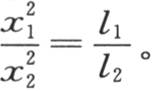 因此,所讨论的这两个距离相互之间的比和粗细的平方根的比相同。
因此,所讨论的这两个距离相互之间的比和粗细的平方根的比相同。
79 【17】 如果粗细相等而所组成的物质不同的两个金属棒被涂上相同的敷层,因而使它们有相同的外热导率 【18】 ,并且如果它们在它们的端点受到相同温度的作用,那么,热就因得到最大热导率而最容易被传导,并且传到离原点最远的距离。为了相互比较从共同原点到获得同一固定温度的点的距离x1 和x2 ,在用k1 和k2 表示这两种物质各自的热导率后,我们应当解方程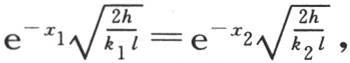 所以,
所以,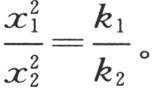
因此,两个热导率的比是从共同原点到获得同一固定温度的点的距离的平方的比。
80 容易确定在单位时间内有多少热流过达到其固定状态的这根棒的一个截面:这个量由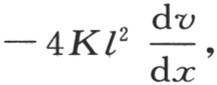 或者是
或者是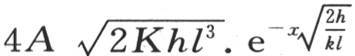 来表示,并且,如果我们在原点取它的值,我们就把
来表示,并且,如果我们在原点取它的值,我们就把 作为在单位时间内从热源流进这一固体的热量的量度;因此,在所有其他条件相同时,热源的消耗与粗细的立方的平方根成正比。
作为在单位时间内从热源流进这一固体的热量的量度;因此,在所有其他条件相同时,热源的消耗与粗细的立方的平方根成正比。
从x为0到x为无穷取积分∫8hlv·dx,我们会得到相同的结果。
第六节 闭空间的加热
81 在下面的问题中我们再利用第72目中的定理,这个问题的解提供有益的应用;它在于确定闭空间的加热程度。
设想任一形式的一个闭空间,它充满空气,且处处封闭,边界的所有部分都是同质的,并且有共同的厚度e,厚度e非常小,以至于外表面与内表面的比和1相差无几。这个边界所限定的这一空间由一个其作用恒定的热源加热;例如,通过一个保持恒温α、面积为σ的面来加热。
此处我们只考虑包含在这个空间中的空气的平均温度,而不考虑这个气团的不均匀分布,因此我们假定,有某种原因不断混合这团空气的所有部分,并使它们的温度变成均匀的。
我们首先看到,不断离开热源、在周围空气中扩散自己、并且贯穿到这个边界所围成的这一气团中去的热,部分地弥散到表面,并进入外部空气,我们假定外部空气保持较低且永恒的温度n。内部空气愈来愈被加热,这个固体的边界亦如此:这个温度系统逐渐趋近于一个终极状态,这个终极状态是这个问题的目的,并且,只要热源面σ保持温度α,外部空气保持温度n,它就具有自行存在并保持自身不变的性质。
在我们所希望确定的这个永恒状态中,空气保持一固定温度m;这个固体边界的内表面s的温度也有一个固定值a;最后,限定这个包壳的外表面s保持一小于a但大于n的温度b。量σ,α,s,e和n是已知的,量m,a和b是未知的。
加热程度在于温度m超过外部空气温度n的超出量;这个超出量显然依赖于加热面的面积σ,并且依赖于它的温度α;它也依赖于这个包壳的厚度e,依赖于界定它的面的面积s,依赖于热据以贯穿到内表面或与之相反的能力;最后,依赖于组成这个包壳实体的热导率:因为,如果这些因素中任何一个被改变而其他因素保持不变,那么加热程度仍然会发生变化。问题是要确定所有这些量怎样结合到m-n的值中去。
82 这个固体的边界由各保持一固定温度的两个相等的面所限定;因此,包围在这两个面的两个相对部分和围绕这两部分基底的周线所作的法线之间的每一棱柱基元都处在相同的状态之中,就像它属于包围在两个保持不同温度的平行平面之间的一个无穷固体一样。组成边界的所有棱柱基元沿它们的整个长度相接触。与内表面等距的这个物体的那些点,无论它们属于哪一个棱柱,都有相同的温度;所以,在与这些棱柱的长垂直的方向上,不可能有任何热传导。因此,这种情况与我们已经讨论过的情况相同,并且,我们应当对它应用在前面几目中所叙述过的线性方程。
83 因此,在我们要考虑的这个永恒状态中,在单位时间内由面σ所提供的热流量与在相同时间内从内部空气进入这个包壳的内表面的热流量相等;它也与在单位时间内过这个固体包壳内的一个中间截面的热流量相等,这个中间截面由一个与围成这个包壳的面相等且平行的面所构成;最后,这同一热流量还与过这个固体包壳外表面而从这个固体包壳流过并被耗散到空气中去的热量相等。如若这4个热流量不等,那么某种变化就必然在温度的这个状态中出现,这与假定矛盾。
第一个量由σ(a-m)g来表示,g表示属于热源面σ的外热导率。
第二个量是s(m-a)h,系数h是受热源作用的面s的外热导率的量度。
第三个量是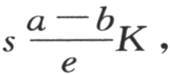 系数K是形成这个边界的同质物质的固有热导率的量度。
系数K是形成这个边界的同质物质的固有热导率的量度。
第四个量是s(b-n)H,H表示面s的外热导率,热离开这个面而被耗散到空气中去。由于围成这个包壳的这两个面的状态差,所以系数h和H可能有非常不同的值;它们被假定为是已知的,系数K也一样:这时,为了确定三个未知量m,σ和b,我们有三个方程:σ(a-m)g=s(m-a)h,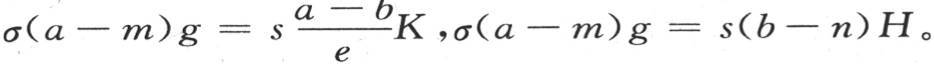
84 m的值是这个问题的特殊对象。它可以通过把这些方程写成如下形式而得到: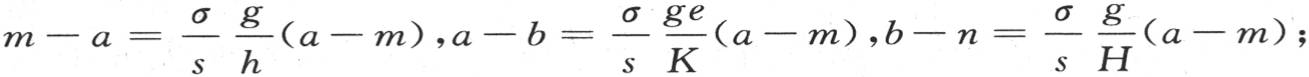 相加,并用P表示已知是
相加,并用P表示已知是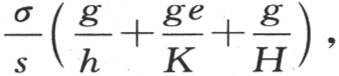 则有m-n=(α-m)P;因此我们得到
则有m-n=(α-m)P;因此我们得到
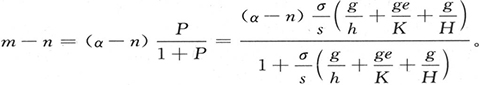
85 这个结果表明,加热程度m-n怎样依赖于构成这个假定的已知量。我们要指出由它导出的一些主要结果 【19】 。
第一,加热程度m-n与热源温度超过外界空气温度的超出最成正比。
第二,m-n的值不依赖于包壳的形状,也不依赖于它的体积,而只依赖于热所由之发出的面和得到它的面的比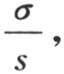 还依赖于这个边界的厚度e。
还依赖于这个边界的厚度e。
如果我们使热源面σ增加一倍,则加热程度不会翻倍,它只是根据这个方程所表示的某个规律而增加。
第三,规定热作用的所有特定系数,即g,K,H和h,与厚度e一起,在m-n的值中构成一个单一的因素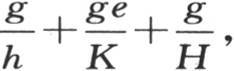 它的值可以通过观察来确定。
它的值可以通过观察来确定。
如果我们使这个边界的厚度e增加一倍,那么如果在构成这个边界时,我们用了其固有热导率是原来两倍的物质,则我们会得到同样的结果。因此,若使用的是不良导热物质,则允许我们的边界厚度就小;所得到的这个效应只依赖于比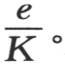
第四,如果热导率K是0,我们得到m=α;即内部空气呈热源温度:如果H为0,或者h为0,情况亦如此。换言之,由于这时热不能耗散到外部空气中去,所以这些推论是显然的。
第五,正如我们在后面将要表明的那样,我们假定已知量g,H,h,K和α的值可以直接由实验来确定;不过在实际问题中注意到对应于已知的σ值和α值的m-n的值就够了,并且,借助于方程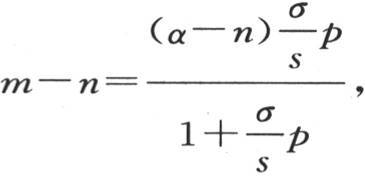 我们可以用这个值来确定整个系数
我们可以用这个值来确定整个系数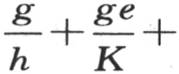
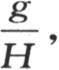 方程中的p表示所求的这个系数。在这个方程中,我们应当不用
方程中的p表示所求的这个系数。在这个方程中,我们应当不用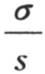 和α-n而代之以我们假定为已知的这些量的值和观察将使之成为已知的m-n的值。由此可以导出p的值,然后我们可以把这个公式应用到任何其他的情况中去。
和α-n而代之以我们假定为已知的这些量的值和观察将使之成为已知的m-n的值。由此可以导出p的值,然后我们可以把这个公式应用到任何其他的情况中去。
第六,系数H以和系数h同样的方式结合到m-n的值中;所以,无论这个面指的是内表面还是外表面,它的状态,或者覆盖它的这个包壳的状态,都产生同样的作用。
如果我们在这里不处理一些其结果可能有直接用处的全新问题,我们可能会认为注意这些不同的结论没有什么用。
86 我们知道,有生命的物体保持一明显固定的温度,我们可以把它看做是与它们生活于其中的介质温度无关的。正如其燃烧已变成均匀的燃烧物质一样,这些物体也可以说是恒定的热源。这样,借助于前面那些注记,我们就可以精确地预见和控制在人员大量集中的场所的温升。如果在这里我们观察到在给定环境下的温度计的高度,那么如果当集中在这同一空间的人数变得非常大时,我们就可以预先确定这个温度计的高度将是怎样的。
实际上,有几个次要条件左右这个结果,例如包壳各部分的不同的厚度,它们形状的差异,开口所产生的影响,空气中不同的热分布等。因此,我们不能严格应用由分析所给出的这些规律;不过这些规律本身是有价值的,因为它们包含这个问题的真正原理:它们拒斥含糊推理和无用的或混乱的努力。
87 如果这同一空间由两个或更多的不同类型的热源所加热,或者,如果第一个包壳本身包含在第二个包壳中,并且由一层空气将它们分开,那么同样地,我们能够很容易地确定加热程度和各表面的温度。
如果我们假定,除第一个热源σ之外,还存在第二个加热面π,它的恒定温度是β,外热导率为j,那么,在所有其他名称都保持不变时,我们有下面的方程:

如果我们只假定一个热源σ,并且如果第一个包壳本身包含在第二个之中,s,h,K,H,e表示第一个包壳的各因素,与之对应,s′,h′,K′,H′,e′表示第二个包壳中的各因素,p表示围绕第二个包壳外表面的空气的温度,那么,我们就得到如下的方程: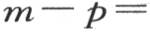
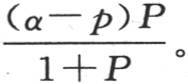 量P表示
量P表示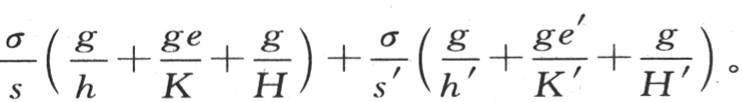 如果我们有三个或更多的连续包壳,我们会得到一个类似的结果;由此我们得出结论,由空气分开的这些固体包壳,尽管它们的厚度可能很小,但却非常有助于增加加热的程度。
如果我们有三个或更多的连续包壳,我们会得到一个类似的结果;由此我们得出结论,由空气分开的这些固体包壳,尽管它们的厚度可能很小,但却非常有助于增加加热的程度。
88 为了使这个注记更明显,我们比较从受热面所逃逸的热量,和若包围这同一固体的这个面以一个充满空气的间隙与这个固体分开时这个固体所失去的热量。
如果物体A由一个恒定原因加热,因此它的表面保持一固定温度b,空气保持较低的温度a,那么,在单位时间内过单位面积逃逸到空气中去的热量就由h(b-a)来表示,h是外热导率的量度。因此,为了使这个物体保持固定温度b,这一热源,无论它怎样,都应当提供与hS(b-a)相等的热量,S表示这个固体的面积。
假定一个极薄的壳层从物体A上给拆下来,由一个充满空气的间隙使它与这个固体分开;并且假定这同一固体A的表面仍保持温度b。我们看到,保持在这个壳层和这个物体之间的空气将受热,并得到比a更高的温度a′。这个壳层本身将达到一个永恒状态,并向固定温度为a的外部空气传导这个物体所失掉的所有的热。因此,从这个固体所逃逸的热量不是hS(b-a),而是hS(b-a′),因为我们假定,这个固体的新的表面和界定这个壳层的两个面也有相同的外热导率h。显然,热源的消耗会比它开始时要少。问题是要确定这些量的精确比。
89 设e是这个壳层的厚度,m是它内表面的固定温度,n是它外表面的温度,K是它的内热导率。作为经过这个固体表面而离开这个固体的热量表达式,我们有hS(b-a′)。
作为贯穿到这个壳层内表面的热量表达式,我们有hS(a′-m)。
过这同一壳层任一截面的热量表达式,是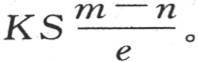
最后,过外表面而进入空气的热量表达式,是hS(n-a)。
所有这些量肯定相等,因此,我们有下述方程: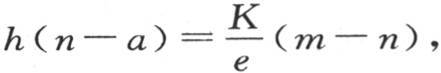 h(n-a)=h(a′-m),h(n-a)=h(b-a′)。
h(n-a)=h(a′-m),h(n-a)=h(b-a′)。
此外,如果我们写出恒等方程h(n-a)=h(n-a),并以下述形式整理它们:n-a=n-a,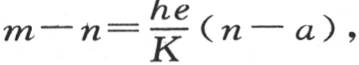 a′-m=n-a,b-a′=n-a,那么相加,我们就得到
a′-m=n-a,b-a′=n-a,那么相加,我们就得到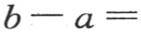
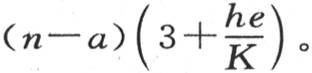
在原来这个固体的表面与空气自由连通时,它所失去的热量是hS(b-a),现在它是hS(b-a′)或hS(n-a),它等于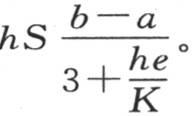
在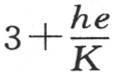 比1的这个比中,第一个量比第二个量大。
比1的这个比中,第一个量比第二个量大。
因此,其表面直接与空气连通的一个固体,为了保持温度b,所需要的热应当比当它的极面不是附在这个固体上,而是由任意小的充满空气的间隙使它与这个固体分开时,为保持它的温度b所需要的热,多三倍多。
如果我们假定厚度e无穷小,那么所失去的热量比就是3,若K无穷大,则这个比仍是这个值。
我们不难解释这个结果,因为,由于热不贯穿几个面就不能逃逸到外部空气中去,所以当插入面的数目增加时,流出的热量就肯定减少;不过,如果我们还不能使这个问题纳入分析,那么我们就仍然不能得到对这种情况的任何精确的判断。
90 在上一目中,我们没有考虑经过分开这两个面的空气层的辐射作用;然而因存在一部分直接穿过这种中间空气的热,所以这个条件会使这个问题有所改变。这样,为了使这个分析目的更清晰,我们假定两个面之间的间隙没有空气,这个受热物体由任意多个彼此分开的平行薄层包住。
如果经过保持温度b的这个固体的表面而逃离这个固体的热本身在真空中自由膨胀,并由保持较低温度a的平行面所接受,那么,在单位时间内经过单位面积所扩散的热量就与这两恒温的差(b-a)成正比:这个量由H(b-a)表示,H是与h不同的相对热导率的值。
因此,使这个固体保持其初始状态的热源,在每一单位时间内,都应当提供与HS(b-a)相等的热量。
现在,在总是假定这个固体受任一使它表面保持温度b的外因作用时,在由真空间隙分开的几个连续薄层包住这一物体表面的情况中,我们应当确定这个消耗的新值。
设想这整个温度系统已经成为固定的;设m是第一个薄层的内表面的温度,这个面必然与这个固体的表面相对,设n是这同一薄层的外表面的温度,e是这个薄层的厚度,K是它的热导率;同时用m1 ,n1 ,m2 ,n2 ,m3 ,n3 ,m4 ,n4 等等表示不同薄层的内表面和外表面的温度,用K,e表示这些薄层的热导率和厚度;最后,假定所有这些面都处在与这个固体表面相同的状态中,因此,系数H的值对于它们是相同的。
贯穿到对应于任一下标i的一个薄层的内表面的热量是HS(ni-1 -mi ),过这个薄层的热量是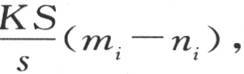 从它外表面所逃逸的热量是HS(ni -mi+1 )。这三个量,以及属于其他薄层的所有这样的量,都相等;所以,通过比较所研究的所有这些量和它们的第一个量HS(b-m1 ),我们可以建立方程;因此,用j表示薄层数,则我们有:
从它外表面所逃逸的热量是HS(ni -mi+1 )。这三个量,以及属于其他薄层的所有这样的量,都相等;所以,通过比较所研究的所有这些量和它们的第一个量HS(b-m1 ),我们可以建立方程;因此,用j表示薄层数,则我们有:
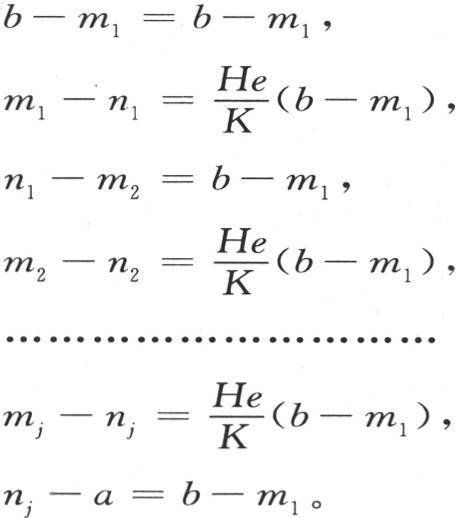
把这些方程相加,我们得到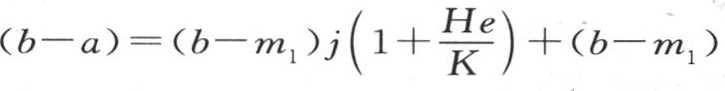 。 【20】
。 【20】
当物体A的表面向保持温度a的一个固定面发射其射线时,热源为使物体A的表面保持温度b所应当消耗的热量,是HS(b-a)。当我们在这个物体A的表面和保持温度a的固定面之间放进j个单独薄层时,这个消耗量是HS(b-m1 )或者是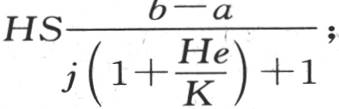 因此,热源在第二种假设中所应当提供的热量,比在第一种假设中所要提供的少得多,这两个量的比是
因此,热源在第二种假设中所应当提供的热量,比在第一种假设中所要提供的少得多,这两个量的比是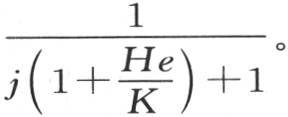 如果我们假定这些薄层的厚度e是无穷小的,这个比就是
如果我们假定这些薄层的厚度e是无穷小的,这个比就是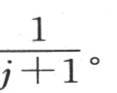 这样,热源的消耗就与包住这个固体表面的薄层数成反比。
这样,热源的消耗就与包住这个固体表面的薄层数成反比。
91 对这些结果,以及对在连续包壳之间的间隙被空气填满时我们对所获得的那些结果的考察,清楚地解释为什么这种表面分开和空气介入非常有助于保热。
另外,在我们假定热源是外部的,并且从热源所发出的热连续经过不同的可以透热的包壳和它们所包住的空气时,分析提供类似的结论。这就是当实验者使温度计受太阳光的作用,并且温度计被几层玻璃罩罩住,其中各层都包住一些空气时所发生的情况。
由于类似的原因,较高的大气层的温度就比地球表面的温度要低得多。
一般来说,关于闭空间中空气的加热的这些定理可以推广到许多不同的问题上去。如在温室、烘房、羊圈和车间等的情况中,或者在诸如医院、营房和会堂等许多土木建筑中,在我们希望精确预见和控制温度时,回到这些定理上来是有用的。
在这些不同的应用中,我们应当注意一些改变这些分析结果的其他附加情况,如包壳不同部分的厚度不等,空气的介入等等;不过,这些细节会使我们离开我们的主要目的,我们的主要目的是一般原理的严格论证。
至于其他方面,如刚才所说,我们只考虑了闭空间中温度的永恒状态。此外,我们也能用分析来表示在这之前的变化状态,或者当热源撤掉后开始发生的状态,由此可见,我们也可以确定我们所运用的这些物体的特性或尺寸怎样影响加热的进程和时间;不过,这些研究需要一种不同的分析,这种分析原理我们将在下面几章中解释。
第七节 三维的均匀热运动
92 到此为止,我们考虑的只是一维情况下的均匀热运动,不过,我们很容易把这同样的原理运用到热在三个垂直方向均匀传导的情况中去。
假定由六个直角面所包围的一个固体的不同的点有由线性方程v=A+ax+by+cz所表示的不同的有效温度,x,y,z是温度为v的一个分子的直角坐标。再假定作用在这个棱柱的六个面上的任一外因使位于这个表面的每一个分子都保持由一般方程

所表示的有效温度,我们要证明,假定使这个固体各个外表面保持它们初始温度的同样这些原因,也足以保持每一个内部分子的有效温度,因此它们的温度也不得不由这个线性方程来表示。
对这个问题的考察是这个一般理论的一个组成部分,它将用来确定任一形状的固体内的变化的热运动的规律,因为,组成这个物体的每个棱柱状分子在一个无穷小的时间内都处在与这个线性方程(a)所表示的相类似的状态中。这样,根据微分学的一般原理,我们很容易从均匀运动的概念导出变化运动的一般方程。
93 为了证明在这个固体的各外表面维持它们的温度时这个物体内部不可能发生变化,只要相互比较在同一时刻内经过两个平行平面的热量就够了。
设b是我们首先假定的与x和y的水平面平行的这两个平面的垂直距离。设m和m′是两个挨得无穷近的分子,其中一个在第一个水平面的上方,另一个在其下方:设x y,z是第一个分子的坐标,x′,y′,z′是第二个的坐标。同样,设M和M′表示由第二个水平面所分开的两个无穷近的分子,相对于这个平面,它们处于与m和m′相对于第一个平面的完全相同的位置;也就是说,M的坐标是x,y,z+b,M′的坐标是x′,y′,z′+b,显然,分子m和m′的距离mm′与分子M和M′的距离MM′相等;另外,设v是m的温度,v′是m′的温度,同样,设V和V′是M和M′的温度,不难看到,两个差v-v′和V-V′相等;事实上,先在一般方程v=A+ax+by+cz中代入m和m′的坐标,我们得到v-v′=a(x-x′)+b(y-y′)+c(z-z′)然后代入M和M′的坐标,我们同样得到V-V′=a(x-x′)+b(y-y′)+c(z-z′)。现在m向m′所发出的热量依赖于使这两个分子分开的距离mm′,并且它与它们的温差v-v′成正比。所传导的热量可以由q(v-v′)dt来表示,系数q的值在某种意义上依赖于距离mm′,且依赖于形成这个固体的物质的质,dt是这一时刻的长度。从M传导到M′的热量,或者是M对M′的作用,同样由q(V-V′)dt来表示,系数q与表达式q(v-v′)dt中的相同,因为距离MM′与mm′相等,并且这两个作用发生在这同一固体中:此外,V-V′与v-v′相等,因此,这两个作用相等。
如果我们选择相互挨得很近的另外两点n和n′,它们经过第一个水平面而传热,那么我们将以同样的方式得到它们的作用与经过第二个水平面传热的相应两点N和N′的作用相等。因此我们得出,在同一时刻内,经过第一个平面的全部热量与经过第二个平面的全部热量相等。从平行于x和z的平面的两个平面、以及从平行于y和z的平面的另外两个平面的比较中,我们可以得到同样的结果。所以,包围在六个直角面之间的这个固体的任何部分,从其每一面所得到的热量,与它通过其相对的面所失去的热量一样多;因此,这个固体的任何部分都不会有温度的变化。
94 由此我们看到,流过所讨论的这些平面之一的一个热流量,在所有时刻内,都是一样的,它对于所有其他平行截面,也是一样的。
为了确定这个恒流量的值,我们把它与已经讨论过的最简单情形中所均匀流过的热量比较一下。这种最简单的情形就是包围在两个无穷平面之间且保持一恒定状态的无穷固体的情况。我们已经看到,在这种情况中,这个物体的不同点的温度由方程v=A+cz来表示;我们继续证明,在这个无穷固体中,在垂直方向上所传导的均匀热流量,与在相同方向中经过六直角面所包围的棱柱所流过的热量是相等的。如果属于第一个固体的方程v=A+cz中的系数c与表示这个棱柱状态的更一般的方程v=A+ax+by+cz中的系数c相同,那么这个等式就必然成立。事实上,由H所表示的这个棱柱中的一个平面垂直于z,由m和μ所表示的两个分子相互挨得很近,其中第一个m在这个平面H的下方,第二个在这个平面的上方,设v是坐标为x,y,z的m的温度,w是坐标为x+α,y+β,z+γ的μ的温度。取第三个分子μ′,它的坐标是x-α,x-β,z+γ,它的温度可以由w′表示。我们看到,μ和μ′在同一水平面上,从连接这两点的线段μμ′的中点所作的垂线经过点m,因此,距离mμ和mμ′相等。m对μ的作用,或者这两个分子中的第一个过平面H向另一个所发出的热量,取决于它们的温差v-w。同样,m对μ′的作用取决于这两个分子的温差v-w′,因为,m和μ的距离与m和μ′的距离是相等的。因此,当用q(v-w)表示在单位时间内m对μ的作用时,我们就用q(v-w′)表示m对μ′的作用,q是一个共同的未知因子,它取决于距离mμ,也取决于这个固体的质。因此,在单位时间内所产生的这两个作用的和是q(v-w+v-w′)。
如果在一般方程v=A+ax+by+cz中,我们用m的坐标,然后用μ和μ′的坐标代替x,y和z,那么我们得到v-w=-aα-bβ-cγ,v-w′=+aα+bβ-cγ。因此,m对μ和m对μ′的这个两作用的和是-2qcγ。
这样,假定平面H属于其温度方程为v=A+cz的无穷固体,也假定我们用m,μ和μ′表示这个固体中的三个分子,第一个分子的坐标是x,y,z,第二个的坐标是x+α,y+β,z+γ,第三个的坐标是x-α,y—β,z+γ;那么,和前一种情况一样,我们有v-w+v-w′=-2cγ。因此,m对μ和m对μ′的这两个作用的和,同无穷固体中由六直角平面所包围的棱柱中的情况相同。
如果我们考虑这个平面H下方另外一点n,对位于该平面上方同样高度的另外两点ν和ν′的作用,则我们会得到一个类似的结果。因此,过这个平面H所产生的所有这种作用的和,也就是说,由于这个表面所分开的这些挨得很近的分子的作用而在单位时间内经过这个面的上边的全部热量,在这两个固体中总相等。
95 这两个固体的第二个,由两个无穷平面所界定,温度方程是v=A+cz,在这个固体中,我们知道在单位时间内流过任一水平截面的单位面积的热量是-cK,c是z的系数,K是热导率;因此,在由六直角平面所包围的这个棱柱中,当表示这个棱柱温度的线性方程是v=A+ax+by+cz时,在单位时间内经过任一水平截面的单位面积的热量,也是-cK。用同样的方法可以证明,在单位时间内均匀流过任一垂直于x的截面的单位面积的热量,由-aK表示,在单位时间内经过垂直于y的一个截面的单位面积的全部热量,由-bK表示。
我们在本目和前两目中所论证的这些定理假定物质内部的热的直接作用限制在极小的距离内,然而,若由每个分子所发出的热辐射线能直接贯穿相当远的距离,则它们仍然成立,不过正如我们在第70目中所注意到的,在这种情形下,必须假定保持这个固体各表面温度的原因在这一物体中总是部分地延伸一有限的深度。
第八节 在已知固体的一个已知点的热运动的量度
96 我们仍然需要确定热理论的某个基本原理,它在于严格定义和测量过一个方向已知的平面而经过实体每一点的热量。
如果热被不均匀地分布在同一物体的分子之间,那么任一点的温度将时刻发生变化。用t表示历经时间,用v表示t时后由坐标为x,y,z的一个无穷小的分子所达到的温度;则这个固体的变化状态就由像v=F(x,y,z,t)这样的一个方程所表示。假定函数F已知,因而我们可以在每一时刻确定任一点的温度;设想我们过点m作平行于x和y平面的一个水平面,并设想我们在这个水平面上引一个其圆心在m上的无穷小圆ω;我们需要确定在时刻dt内从这个固体在这个平面下方的部分经过该圆ω而进入在这个平面上方的那一部分的热量。
与点m挨得极近并且在这个平面之下的所有点,在无穷小时刻dt内,都对在这个平面之上并且与点m挨得极近的所有点发生作用,即位于这个平面一边的每一点都向位于另一边的每一点传热。
我们把向这个平面上方传递一定热量的作用看做是正的,把使热经过平面下方的作用看做是负的。过圆ω所发生的所有部分作用的和,即过该圆任一点从这个平面下方的这个固体的部分进入其上方这一部分的所有热量的和,构成其表达式待求的这个热流量。
不难想到,这个热流量在这个固体的整个范围内可能不一样,并且,如果我们在另一点m′引一个等于前一个的水平圆ω′,那么,在同一时刻内,在这两个平面ω和ω′的上方所出现的两个热量可能不等:这两个量可以互相比较,它们的比是不难确定的数。
97 我们已经知道线性运动和均匀运动情形下这个恒流量的值;因此,在由两个无穷的水平面所包围的固体中,其中一个面保持温度a,另一个保持温度b,对于这个物体的每一部分,这个热流量都是相同的;我们可以把它看做是仅仅发生在垂直方向上的。对应于单位面积和单位时间的这个值,是 e表示这两个平面的垂直距离,K表示热导率:这个固体不同点的温度由方程
e表示这两个平面的垂直距离,K表示热导率:这个固体不同点的温度由方程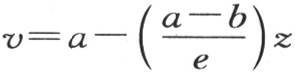 来表示。
来表示。
当问题是由六直角平面构成一个固体,其中这六直角平面两两平行,并且不同点的温度由方程v=A+ax+by+cz表示时,则这种传导就同时沿x,y和z的方向发生;流过平行于x和y平面的一个平面的一个确定部分的热量,在这个棱柱的整个范围内相同;它对应于单位面积和单位时间的值,在z的方向上是-cK,在y的方向上是-bK,在x的方向上则是-aK。
一般地,在我们刚才所引述的两种情形中,垂直流量的值仅仅取决于z的系数和热导率K;这个值总等于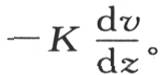
在时刻dt内,流过面积为ω的一个无穷小水平圆、并如此从该圆平面下方的这个固体的一部分进入其在上方这一部分的热量表达式,在所说的这两种情形中,是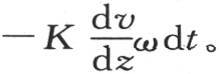
98 现在不难使这个结果一般化,并不难认识到,在由方程v=F(x,y,z,t)所表示的变化的热运动的每一种情形中,它都成立。
事实上,让我们用x′,y′,z′表示这一点m的坐标,用v′表示它的有效温度。设x′+ξ,y′+η,z′+ζ是与点m挨得无穷近的点μ的坐标,它的温度是w;ξ,η,ζ是加到坐标x′,y′,z′上的无穷小量;它们以与x,y和z平行、原点在m上的三直交轴来确定与点m挨得无穷近的分子的位置。对方程v=F(x,y,z,t)微分,并用ξ,η,ζ代替这些微分,我们就得到表示等于v+dv的w值的线性方程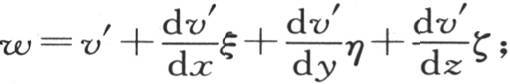 系数v′,
系数v′,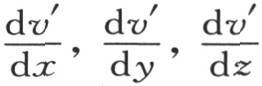 是x,y,z,t的一些函数,其中,属于点m的已知常数值x′,y′,z′代替x,y,z。
是x,y,z,t的一些函数,其中,属于点m的已知常数值x′,y′,z′代替x,y,z。
假定同一点m也属于由六直角平面所包围的一个固体,体积有限的这个棱柱的各个点的有效温度由线性方程w=A+aξ+bη+cζ表示;位于界定这个固体的各个面的分子由某种外因保持这个线性方程所规定的温度。ξ,η,ζ是这个棱柱的一个分子的直角坐标,它们表示原点在m的三个轴,这个分子的温度是w。
如此,如果我们把属于这个微分方程的量v′,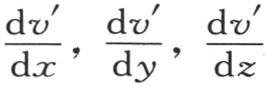 看做是进入这个棱柱方程的常系数A,a,b,c,那么,由方程
看做是进入这个棱柱方程的常系数A,a,b,c,那么,由方程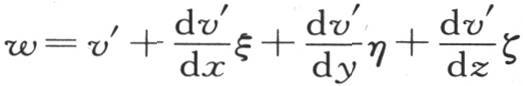 所表示的这个棱柱的状态,就尽可能接近地与这个固体的状态重合;即所有与点m挨得无穷近的分子,无论我们认为是在这个固体中还是在这个棱柱中,都有相同的温度。这个固体与这个棱柱的重合完全类似于曲面和与它们相切的平面的重合。
所表示的这个棱柱的状态,就尽可能接近地与这个固体的状态重合;即所有与点m挨得无穷近的分子,无论我们认为是在这个固体中还是在这个棱柱中,都有相同的温度。这个固体与这个棱柱的重合完全类似于曲面和与它们相切的平面的重合。
由此显然得到,在时刻dt内,在这个固体中流过圆ω的热量与在这个棱柱中流过这同一个圆的热量是相同的;其作用发生在任一效应中的所有这些分子在这两个固体中都有相同的温度。因此,在这两个固体的任一个当中,所讨论的热量都由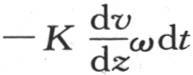 来表示。若圆心为m的圆ω与y轴垂直,则它就是
来表示。若圆心为m的圆ω与y轴垂直,则它就是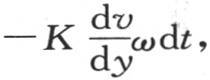 若该圆与x轴垂直,则它是
若该圆与x轴垂直,则它是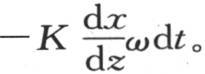
我们刚才所确定的这个热流量的值在这个固体中点点均不相同,它也随时间而异。要是我们设想它在一个单位面积的所有点上都有和点m相同的值,并在单位时间内保持这个值,则这个热流量就由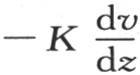 来表示,在y的方向上,它是
来表示,在y的方向上,它是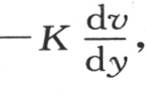 在x的方向上,就是
在x的方向上,就是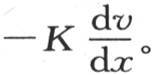 因此,我们在计算中通常采用相对于单位时间单位面积的这个热流量的值。
因此,我们在计算中通常采用相对于单位时间单位面积的这个热流量的值。
99 这个定理一般用于测量热据以经过以任一方式位于其温度随时间变化的一个固体内部的一个平面的一个已知点的速度。过这个已知点m,我们应当在这个平面上作一条垂线,在这条垂线的每一点上,应当做表示它的不同点的有效温度的纵坐标。因此,我们就形成一条平面曲线A,它的横轴是这条垂线。这条曲线的纵坐标的流数,与点m相一致,取异号,表示热经过这个平面时的速度。纵坐标的这个流数被理解为是这条曲线的微元与这个横轴的一条平行线所成夹角的正切。
我们刚才所解释的这个结果是在热理论中最经常应用的结果。我们要讨论这些不同的问题,就不能不对在温度可变的一个物体的每一点的热流量的值形成一个非常精确的思想。必须坚持这个基本见解;我们将要谈的一个例子会更清楚地表明在分析中曾经作出的这种应用。
100 假定边长为π的一个立方体的物质的不同点有由方程v=cosx cosy cosz所表示的不同的有效温度。坐标x,y,z根据三个直交轴来测量,这三个直交轴与该立方体的各个面垂直,原点在这个立方体的中心。这个固体外表面各点的有效温度为0度,还假定有一些外因使得所有这些点都保持有效温度0。在这个假定下,这个物体将愈来愈冷,处在这个物体内部的所有点的温度将发生变化,并且在一个有限时间之后,它们都将达到表面温度0。
现在我们要证明,这个固体的变化状态由方程v=e-gt cosx cosy cosz来表示,系数g等于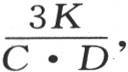 K是形成这个固体物质的热导率,D为密度,C为比热;t是历经时间。
K是形成这个固体物质的热导率,D为密度,C为比热;t是历经时间。
这里我们假定这个方程成立,我们继而考查对它可能作出的应用,以求出过平行于三个直角平面之一的一个已知平面的热量。如果通过坐标为x,y,z的点m,我们作一个垂直于z的平面,那么仿照上一目的方法,我们会发现,在这一点上并过这个平面的热流量的值是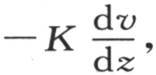 或者是Ke-gt cosx·cosy·sinz。在时刻dt内,过处在这个平面上并且边长为dx和dy的一个无穷小矩形的热量,是Ke-gt cosx cosy sinz dx dy dt。
或者是Ke-gt cosx·cosy·sinz。在时刻dt内,过处在这个平面上并且边长为dx和dy的一个无穷小矩形的热量,是Ke-gt cosx cosy sinz dx dy dt。
因此,在时刻dt内,过这同一平面的全面积的总热量,是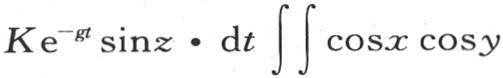
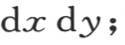 这个二重积分从
这个二重积分从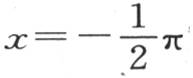 取到
取到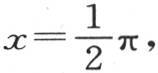 从
从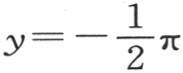 取到
取到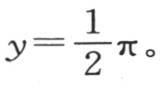 这样,我们就得到作为这个总热量的表达式,4Ke-gt sinz·dt。
这样,我们就得到作为这个总热量的表达式,4Ke-gt sinz·dt。
这时,如果我们相对t从t=0到t=t取积分,那么我们就得到自冷却开始到实际时刻为止的过这同一平面的热量。这个积分是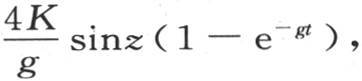 它在表面上的值是
它在表面上的值是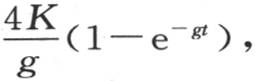 因此,在一无穷时间之后,通过这些面中的某个面所失去的热量是
因此,在一无穷时间之后,通过这些面中的某个面所失去的热量是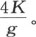 由于这同一推理可用于这六个面中的每一个,因此我们得出,这个固体到完全冷却时所失去的全部热量等于
由于这同一推理可用于这六个面中的每一个,因此我们得出,这个固体到完全冷却时所失去的全部热量等于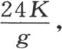 或者是8CD,因为g等于
或者是8CD,因为g等于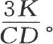 冷却期间所耗散的总热量肯定应当与热导率K无关,因为K只会或多或少地影响冷却速度。
冷却期间所耗散的总热量肯定应当与热导率K无关,因为K只会或多或少地影响冷却速度。
100A 我们可以用另一种方法来确定这个固体在一给定时间内所失去的热量,这将在某种程度上起到检验上述运算的作用。事实上,尺寸为dx,dy,dz的矩形分子的物质是D dx dy dz,因此,为使它从0度变为沸水温度而必须给予它的热量,是CD dx dy dz,如果所需要的是使这个分子升温至v,那么热量的消耗应当是vCD dx dy dz。
由此得到,为了求这个固体在时间t之后的热超过它在0度时所保持的热的超出量,我们应当在区间 之间取多重积分
之间取多重积分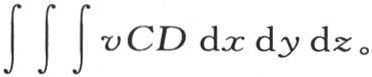
因此,只要用它的值代替v,即用e-gt cosx cosy cosz代替v,我们就得到实际热量超过属于温度0的热量的超出量8CD(1-e-gt );或者,正如我们以前所得到的,在无穷时间之后,是8CD。
在本导言中,我们叙述了为解决与固体中的热运动有关的不同问题所必须了解的所有基本原理,为表明在分析中运用它们的方式,我们给出了它们的某些应用;我们对它们所能作出的最重要的应用,就是由它们导出热传导的一般方程,这是下一章的主题。
第76目注。福布斯(J. D. Farbes)对一端受热的一根长铁棒的温度的研究明确表明,传导率K不是不变的,而是随温度的上升而减少。——《爱丁堡皇家协会会刊》(Transactions of the Rogal Society of Edinburgh),第23卷,第133—146页,第24卷,第73—110页。
第98目注。拉梅(Lamé)在他的《热的解析理论》〔(Théorie Analytique de la Chaleur),第1—8页〕一书中研究了关于在热导率随热流方向而变化的一个物体内热量的一般表达式。——A. F.
注释
【1】 该词各处均可见,传导率(Conductivity)
【2】 它们容量的反比。
【3】 关于这些方程的现代处理,请查阅
黎曼(von B. Riemann),《偏微分方程》(Partielle Differentialgleichungen),不伦瑞克,第二版,1876。第4节,“固体中的热运动”(Bewegung der Wärme in festen Körpern)。
马蒂厄(E. Matthieu),《数学物理教程》(Cours de physique mathématique),巴黎,1873。与热理论的微分方程有关的部分。
托德亨特(I. Todhunter),《拉普拉斯、拉梅和贝塞尔函数》(The Funtions of Laplace, Lamé and Bessel),伦敦,1875。第21、25—29章,它们给出了某些拉梅方法。
韦尔德(E. Verdet),《物理演讲》(Conférences Physique),巴黎,1872〔《全集》,第4卷,第1部分〕。《传导性热扩散教程》(Lecons sur la propagation de la chaleur par conductibilité)。这两本书后附有一个非常广泛的关于热传导的整个领域的文献目录。
对于傅立叶理论的一个有意义的概述和应用,见
麦克斯韦(Maxwell)教授,《热的理论》(Theory of Heat),伦敦,1875(第4版)。第18章,论传导性的热扩散(On the diffusion of heat by conduction)。
汤姆森(W. Thomson)爵士和泰特(Tait)教授,《自然哲学》(Natural Philosophy),第1卷,牛津,1867。第7章,附录D,地球的长期冷却(On the secular cooling of the earth)——A. F.
【4】 《科学院研究报告》,第5卷,巴黎,1826年,第179—213页。——A. F.
【5】 傅立叶在当时所说的“自然哲学”(La Philosophie naturelle),就是我们今天所说的科学,或者是理论科学。——汉译者
【6】 但是在傅立叶1807年的研究报告的注文中说到,热流量与“曲线倾角的正切”成正比。见I. Grattan-Guinness,Josepli Fourier 1768—1830,p98,脚注13。
【7】 此处标题与目录中的不一致,第二章第四节的标题亦如此。——汉译者
【8】 在大多数情况下
【9】 在英译本和法文《文集》本中,这句话都是:“这个量就是hz”。从行文看,“这个量”指的是前文所说的“所耗散的热量就比h少”的那个量。所以,为便于理解,我们加上“所耗散的”。——汉译者
【10】 见傅立叶先生的证明,《物理学化学年鉴》,系列2,第4卷,第128页。——A. F.
【11】 杜隆(Dulong)和珀蒂(Petit)在实验上所研究的更精确的冷却定律,可以在《综合工艺学校学报》〔(the Jour nal de l'Ecole Polytechnique),第11卷,第234—294页,巴黎,1820年〕中,或在雅曼(Jamin)的《物理教程》(Cours de Physique)第47讲中找到。——A. F.
【12】 或左边(临时地)
【13】 英文版中l没有平方,现根据法文《文集》本加上。——汉译者
【14】 列氏〔列奥米尔(Reaumur)〕温标。——A. F.
【15】 k=K
【16】 k=K
【17】 k=K
【18】 因根豪茨(Ingenhousz)(1789),“论导热材料”(Sur les métaux comme conducteurs de la chaleur),《物理学学报》(Journal de Physique),第34卷,第68、380页。格林《物理学学报》(Journal der PhysiK),第1卷。——A. F.
【19】 作者在他发表于《巴黎科普协会通报》(Bulletin par la Société Philomatique de Paris,1818年,第1—11页)的原始论文的摘要中,以一种相当不同的方法表述了这些结果。——A. F.
【20】 在英译本中,此式是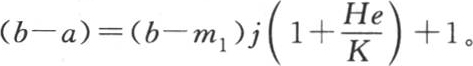
此处依法文《文集》本及其勘误表改正。——汉译者
