第5章　自组织

稳定性、分支和突变

在上一章里我们已看到，随着偏离平衡态的距离的远近，热力学描述采取不同的形式。对于我们来说特别重要的事实是：在远离平衡态时，含有催化机制的化学系统可以导致耗散结构。如将表明的那样，耗散结构对于诸如这类系统的大小和形状，加在其界面上的边界条件等带全局性的特性特别敏感。所有这些特性对于会导致耗散结构的那类不稳定性有着决定性的影响。在有些情况下，外部条件的作用可能会更强，例如宏观尺度上的涨落可能导致不稳定性的新类型。

因此在远离平衡态时，化学动力学和反应系统的时空结构之间出现了意想不到的关系。虽然，决定有关动力学常数和输运系数值的那些相互作用是短程作用（如价键力、氢键、范德瓦尔斯力）。但是，除此之外，有关方程的解还依赖于全局性的特点。这种对全局特性的依赖在靠近平衡态的热力学分支上是无关紧要的，但在工作于远离平衡态条件下的化学系统中，它就变成决定性的了。例如，耗散结构的发生通常要求系统的大小超过某个临界值，而这个临界值是反应扩散过程各参数的一个复杂函数。因此我们可以说，化学不稳定性包含了长程有序性，通过这种长程有序性，系统作为一个整体起作用。

这种全局性的行为使空间和时间的含义深刻化了。几何学和物理学的许多理论都基于通常与欧几里得和伽利略连在一起的关于空间和时间的简单概念上，在这种简单概念中时间是均匀的。时间的平移变换对于物理事件可以不起任何作用。同样，空间也是均匀的，而且是各向同性的，平移和旋转变换也不改变对物理世界的描述。显然，这个空间和时间的简单概念会因耗散结构的发生而打破。耗散结构一旦形成，时间以及空间的均匀性可能就遭到破坏。我们更加接近于亚里士多德所提出的“生物学”的时空观，这我们在序言中已作了简要的叙述。

如果考虑扩散，这些问题的数学表述将涉及到对于偏微分方程的研究。这时组分X_i 的演化将由如下形式的方程组给出

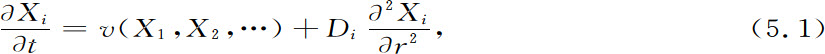
这里的第一项来自化学反应，并且通常具有简单多项式的形式（如第4章“化学反应中的应用”一节中那样），而第二项表示沿坐标r的扩散。为简化记法我们只用了一个坐标r，而一般说来扩散是发生在三维几何空间中的。这些方程还必须附加边界条件（通常给出在边界上的浓度或流）。

能用这类反应扩散方程描述的现象，其种类之繁多实在令人吃惊。这正是为什么要把对应于热力学分支的那个解看做是“基本解”的原因。其他的解可以由逐级的不稳定性求得，这些逐级的不稳定性是在离平衡态的距离增加的时候发生的。不稳定性的这些类型可以用所谓分支理论的方法来研究（Nicolis，Prigogine，1977）。从原则上说，很简单，所谓“分支”就是方程对于某个临界值出现了新的解。例如，假设我们有一个化学反应，对应于如下的速率方程（McNeil，Walls，1974）：

很清楚，对于R＜0，唯一与时间无关的解是X＝0。在点R＝0处，我们有一个新的分支，出现一个新解即X＝R（参见图5.1），并且用第4章“化学反应中的应用”一节所讲解的线性稳定性的方法可以证明，解X＝0将变得不稳定，而解X＝R将是稳定的。通常，在增加某特征参数p（如布鲁塞尔器模式中的B）的值时，我们得到逐级分支。在图5.2中，对于值p₁ 我们有一个解，而对于值p₂ 有多重解。

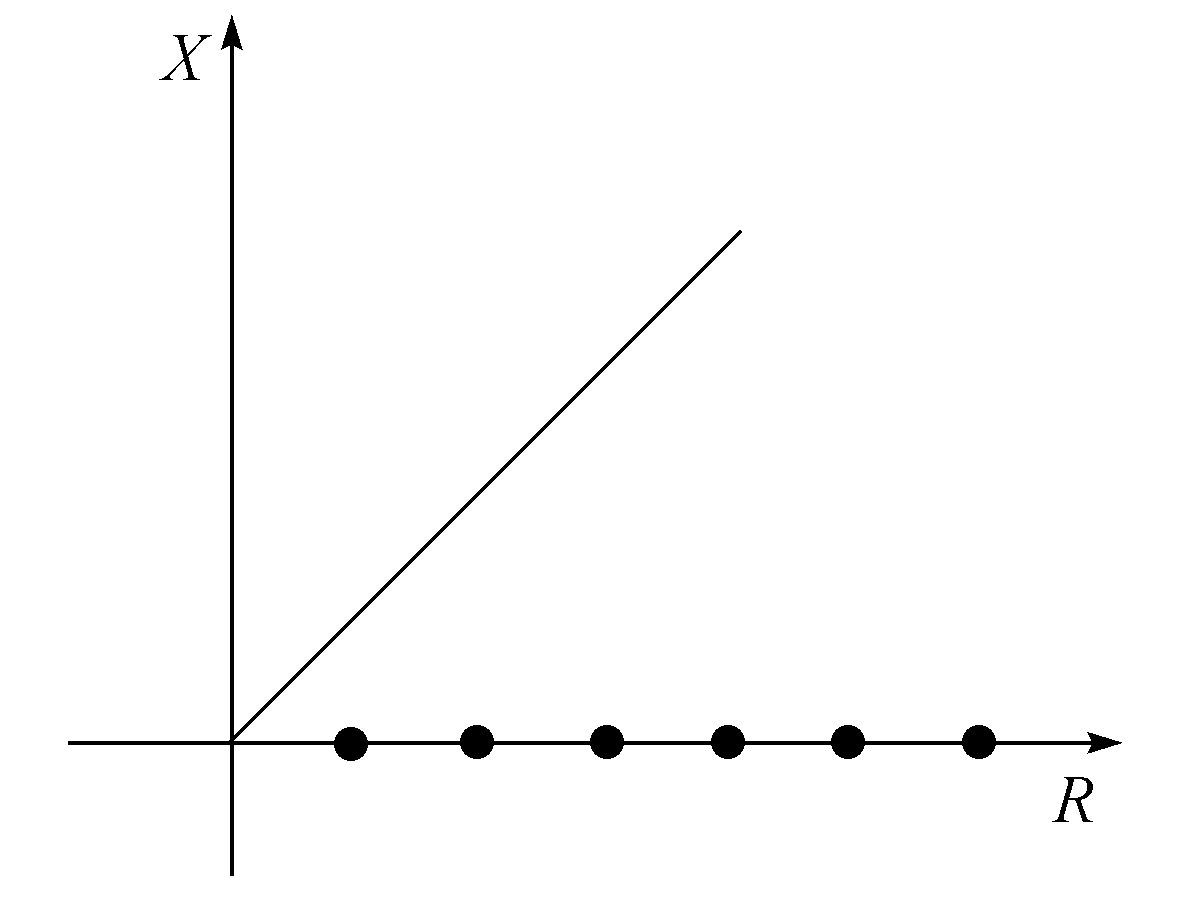
图5.1　方程5.2的分支图

粗实线和点分别表示稳定分支和不稳定分支。

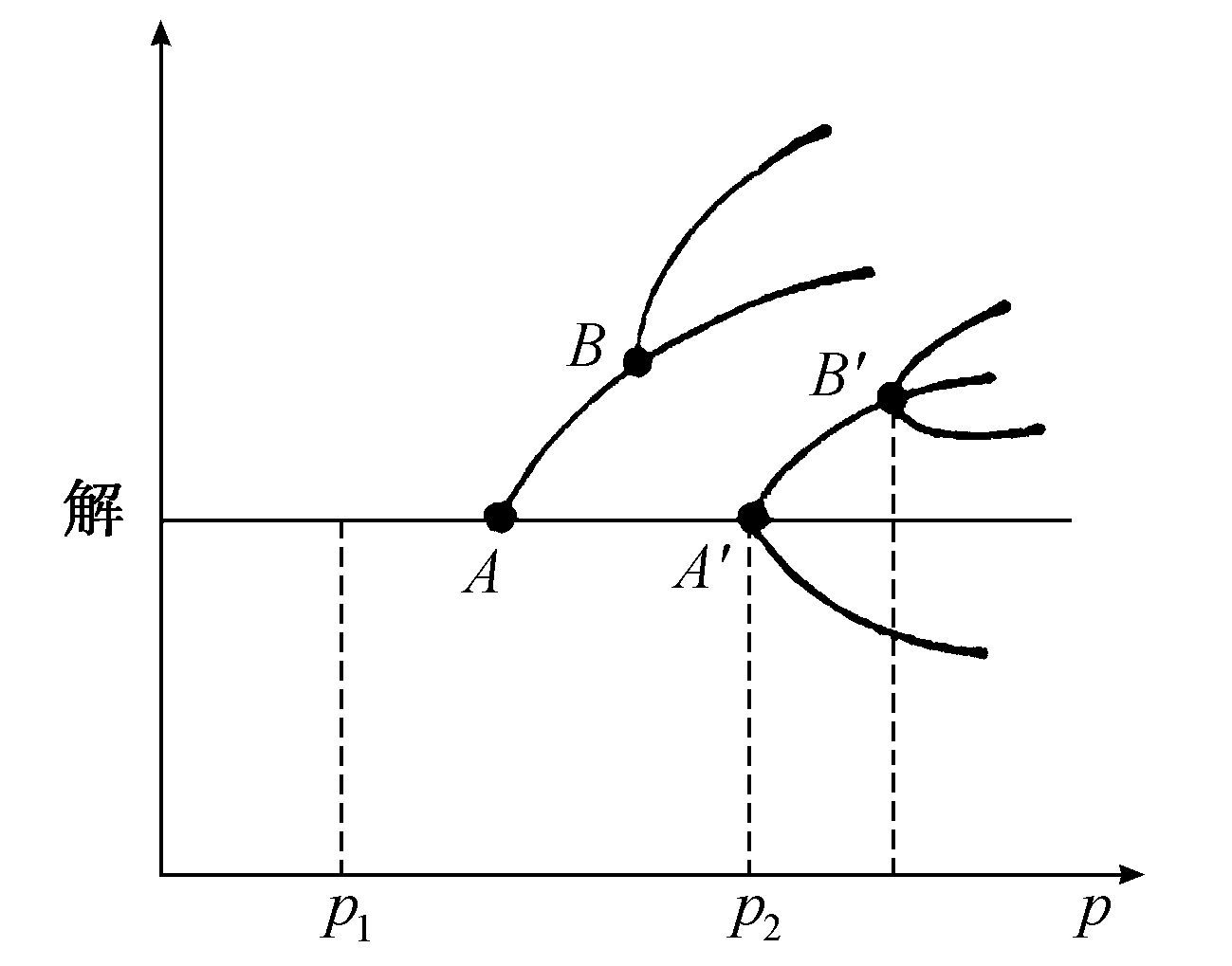
图5.2　逐级分支

A和A′代表来自热力学分支的一级分支点。B和B′代表二级分支点。

有趣的是，在某种意义上说，分支把历史引入到物理学及化学中来，而“历史”这个要素过去似乎只是留给研究生物、社会以及文化现象的学科用的。考虑图5.2的分支图所代表的系统，假设由观察所知，该系统处在C态，而且是通过p值的增加到达这里的，那么对这个C态的解释就暗含了对于该系统先前历史的了解，即该系统一定通过了分支点A和B。

对于具有分支的系统的任何描述都同时含有决定论的和概率论的两种因素。系统在两个分支点之间遵守诸如化学动力学定律之类的决定论规律；但在分支点的邻域内，则涨落起着根本的作用，并且决定系统将要遵循的“分支”。对此我们将在第6章作详细探讨。分支的数学理论通常是非常复杂的，它常包含十分枯燥的展开式。但也有一些情况，可以使用精确的解。这种系统的一个非常简单的情况是由托姆（René Thom，1975）的突变理论给出的。当在方程5.1中忽略扩散的时候，以及当这些方程是从势函数中导出的时候，可以应用这个突变理论。就是说，方程取如下形式：

其中V是一种“势函数”。这是一种很例外的情况。但是只要能满足这个理论的条件，就可以通过寻找使定态的稳定性发生变化的那些点来对方程5.3的解进行一般的分类。托姆把这些点称为“突变的系综”。

稍后，我们将在本章“分支的可解模型”一节中叙述另一类型可以使用精确的分支理论的系统。

最后，在自组织理论中起重要作用的另一个一般的概念是结构稳定性的概念。作为一个简单说明，我们考查和所谓“捕获物-捕获者竞争”相应的洛特卡-沃尔特拉方程的一个简化形式：

在（x，y）相空间中我们有一个由无穷个闭合轨道所组成的集合包围着原点（图5.3）。现在我们把方程5.4的解和方程

的解对比一下，在后一种情况，甚至对于参数a（a＜0）的最小值，点x＝0，y＝0，也是渐近稳定的。该点作为相空间中所有轨道收敛的端点，如图5.4所示。按定义，方程5.4叫做对“涨落”是“结构不稳定”的。这个涨落略为改变了x和y之间相互作用的机制，引入了类似出现在方程5.5中的项（不过这些项很小）。

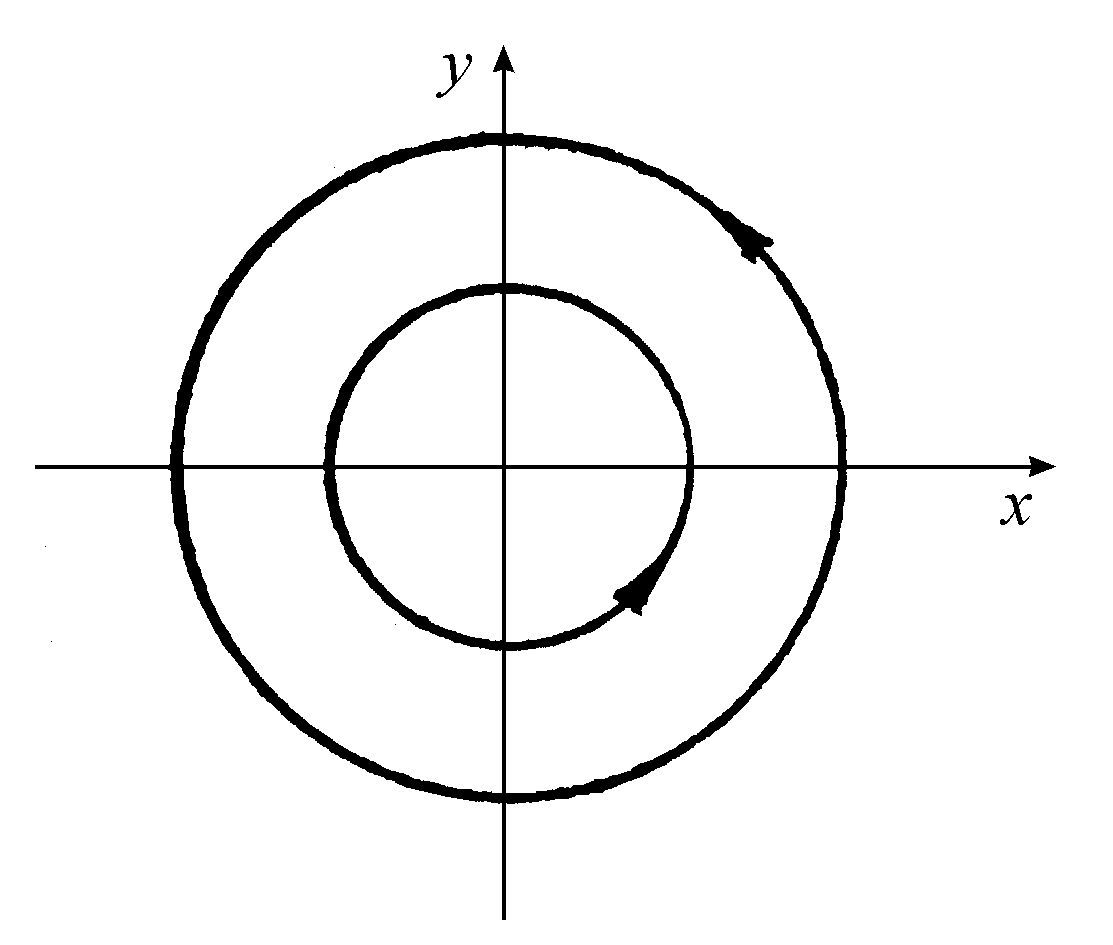
图5.3　方程5.4的轨道

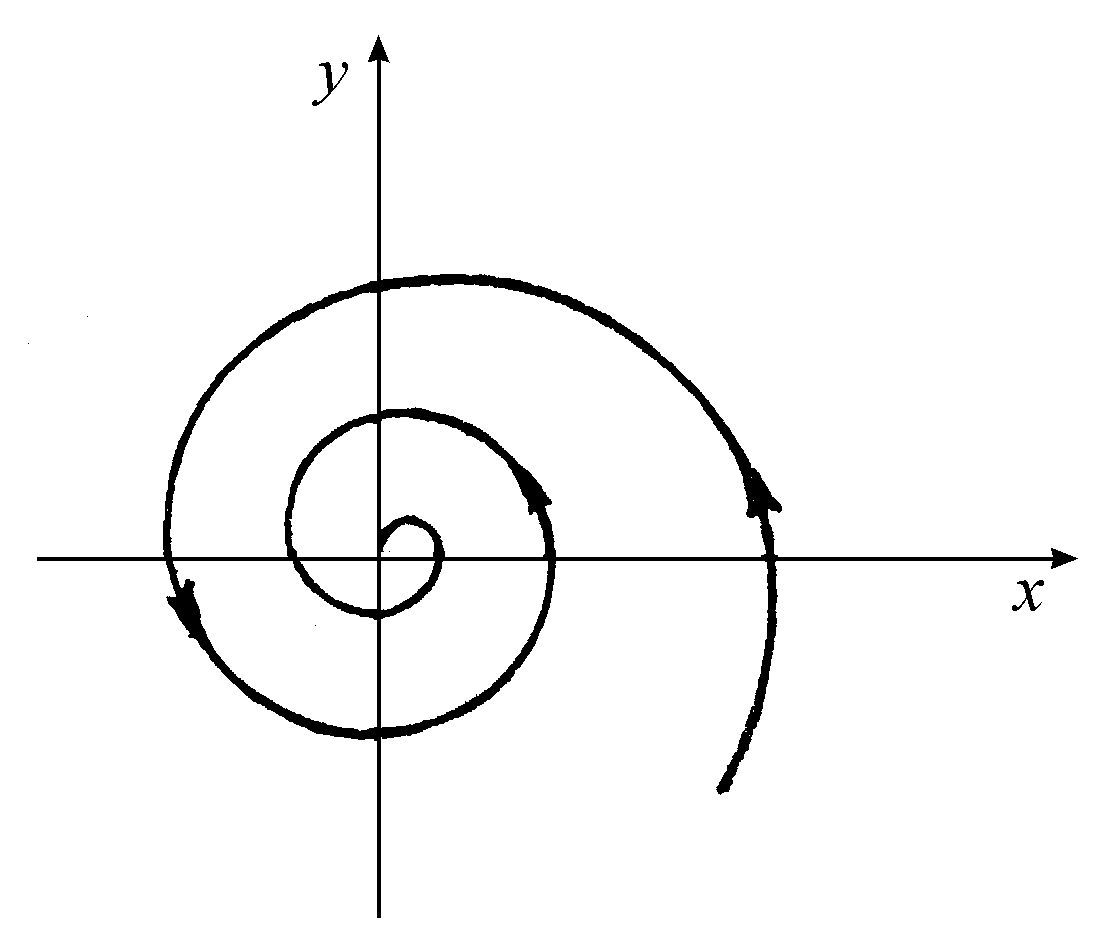
图5.4　方程5.5的轨道

这个例子似乎有点人为的性质，但是用它可以考虑某种聚合过程的化学反应模式，其中聚合物是由泵入系统的分子A和B组成的。假设该聚合物有如下的分子构型：

A B A B A B …

假设产生这种聚合物的反应是自催化的，那么如果发生了错误，并出现了如下的变态聚合物

A B A A B B A B A …

则由于修改了自催化机制，这种变态聚合物就可能在系统中增殖。艾根（Manfred Eigen）提出了包括这种特性的有益的模型，并且证明了在理想情况下，对于聚合物复制时所发生的错误，系统将向着最佳稳定性进化（Eigen，Winkler，1975）。他的模型基于“交叉催化”的思想。核苷酸产生蛋白质，蛋白质又反过来产生核苷酸。

这种导致生成反应的环状网络被称做超环。当这样的网络彼此竞争时，它们显示出通过变异和复制向更大的复杂性进化的能力。艾根和舒斯特在最近的工作中（Eigen，Schuster，1978）提出了与原始复制和翻译装置的分子组织作用有关的“现实性超环”模型。

结构稳定性的概念看来是用最紧凑的方法表达了创新的思想，显示系统出现了原来没有的新机制和新物种。我们将在本章关于生态学的一节中给出一些这方面的简单例子。

分支：布鲁塞尔器

我们已在第4章中介绍过这个模型。它的重要性来自这样的事实：它给出各种各样的解（如极限环、非均匀定态、化学波），这些解正具有我们在离平衡足够远的现实世界的系统中所观察到的类型。如果包括扩散，布鲁塞尔器的反应扩散方程取如下形式（见式4.58和4.59，详见Nicolis，Prigogine，1977）：

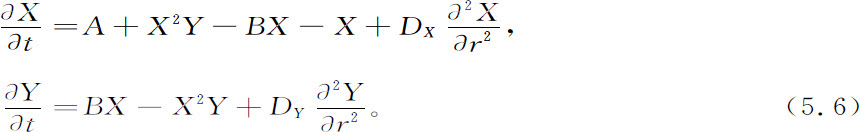
假如给出边界上的浓度值，然后我们寻找下面形式的解（见式4.60）：

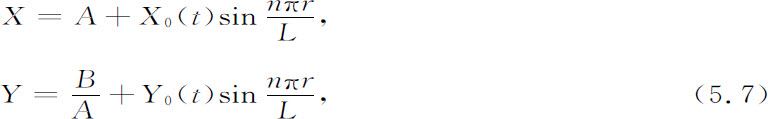
其中n为整数，且X₀ ，Y₀ 仍和时间有关。这些解满足边界条件：对于r＝0和r＝L，有X＝A，Y＝B/A。于是我们可以应用线性稳定性分析并得到色散方程，它把ω和由式5.7中整数n所给出的空间相关性关联起来。

结果如下：不稳定性可以用不同的方式出现。两个色散方程可以有两个共轭的复根，并且在某点，这些根的实部为零。这就是引起第4章中所研究的极限环的情况，在文献中常称做霍普夫分支（Hopf，1942）。第二种可能性是，我们得到两个实根，其中之一在某临界点处变为正的。这就是引起空间非均匀定态的情况，我们可以称之为图林分支，因为是图林第一个在他关于形态发生学的经典论文中（Turing，1952）注意到这种化学动力学里的分支的可能性。

现象的多样性甚至还要大些，因为极限环还可以是与空间有关的，那样就会引起化学波。图5.5中画出了和图林分支对应的化学非均匀定态，而在图5.6中示出了化学波的模拟情况。这些相干现象中究竟哪一个能够实现，要取决于扩散系数D的值，或者说得更好一点，取决于比值D/L² 。当这个参数变成零时，我们得到极限环，即“化学钟”，而非均匀定态只能出现在D/L² 足够大的时候。

图5.5　定态耗散结构

实线为计算的结果，虚线为计算机模拟的结果，其参数为：D_x ＝1.6×10^-3 ，D_y ＝8×10^-3 ，A＝2，B＝4.17。

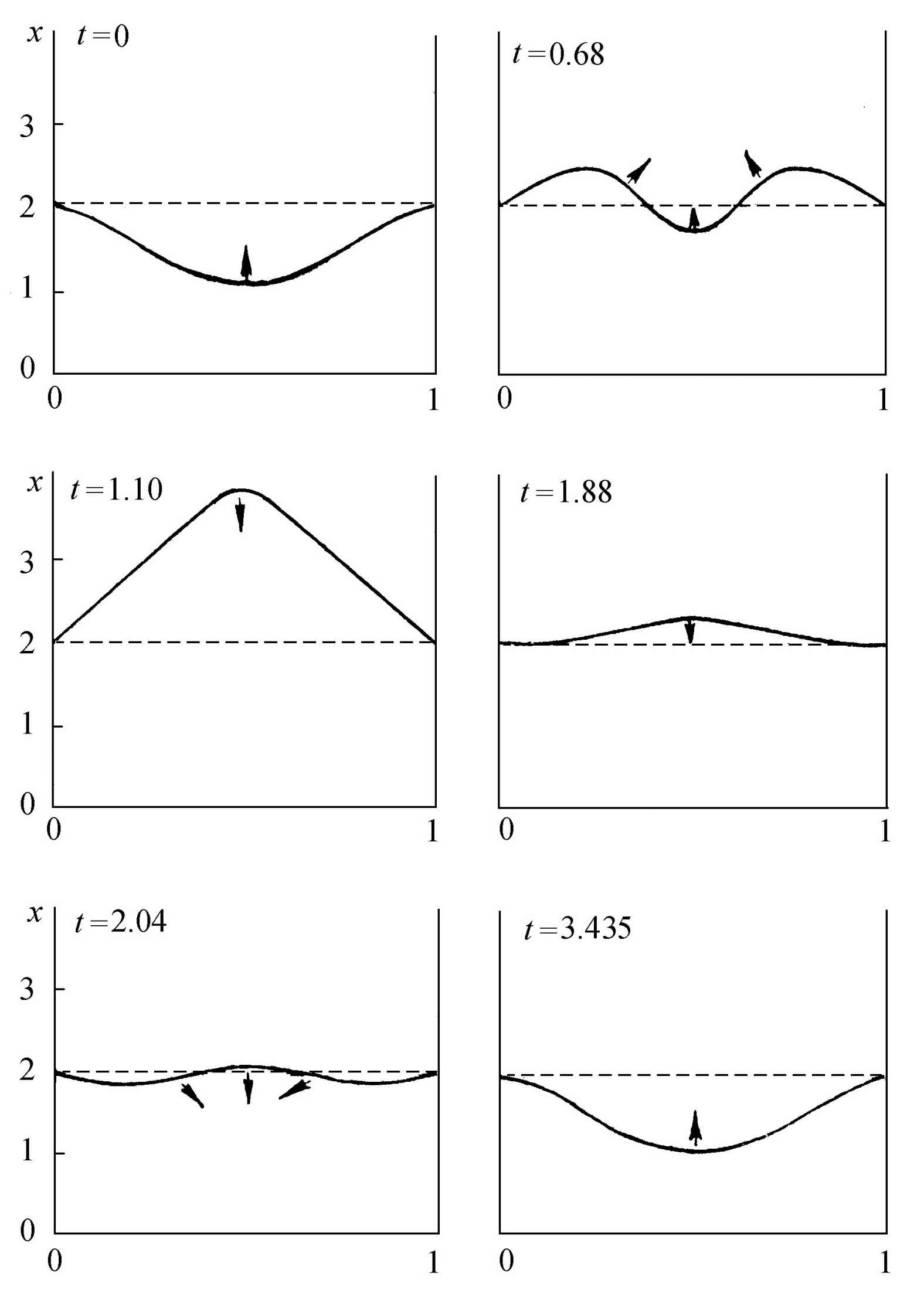
图5.6　计算机模拟的一个化学波

其参数为：D_x ＝8×10^-3 ，D_y ＝4×10^-3 ，A＝2，B＝5.45。

局部化的结构也可以从这个反应的模式得出，只要我们把初始物质A和B（见方程4.57）通过系统而扩散考虑在内。

当然，如果考虑二维或三维的情况，耗散结构的丰富程度还会极大地增长。例如在至今所讨论的均匀系统中，我们还会看到极性的出现。图5.7和图5.8示出在具有不同扩散系数值的二维圆系统中的第一分支。在图5.7中，浓度保持径向的各向同性。而在图5.8中我们看到出现了所谓的优惠增益（Privileged access）。这对于形态学的应用是很有趣的。在那里，第一阶段中的一步对应着在原来处于球对称态的系统中出现了梯度。

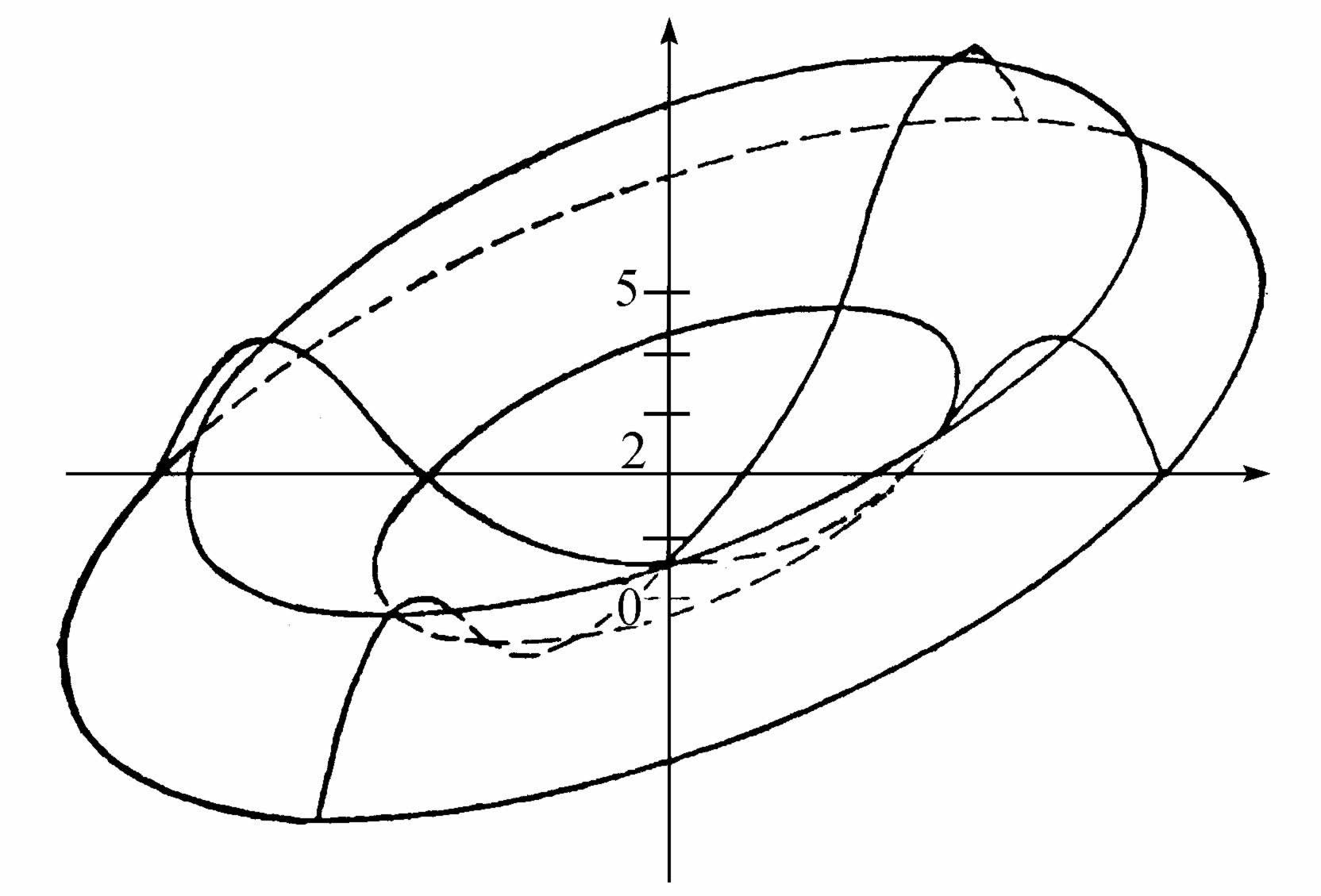
图5.7　圆柱形对称的二维定态耗散结构（由计算机模拟得出）

其参数为：D_x ＝1.6×10^-3 ，D_y ＝5×10^-3 ，A＝2，B＝4.6，圆半径R＝0.2。

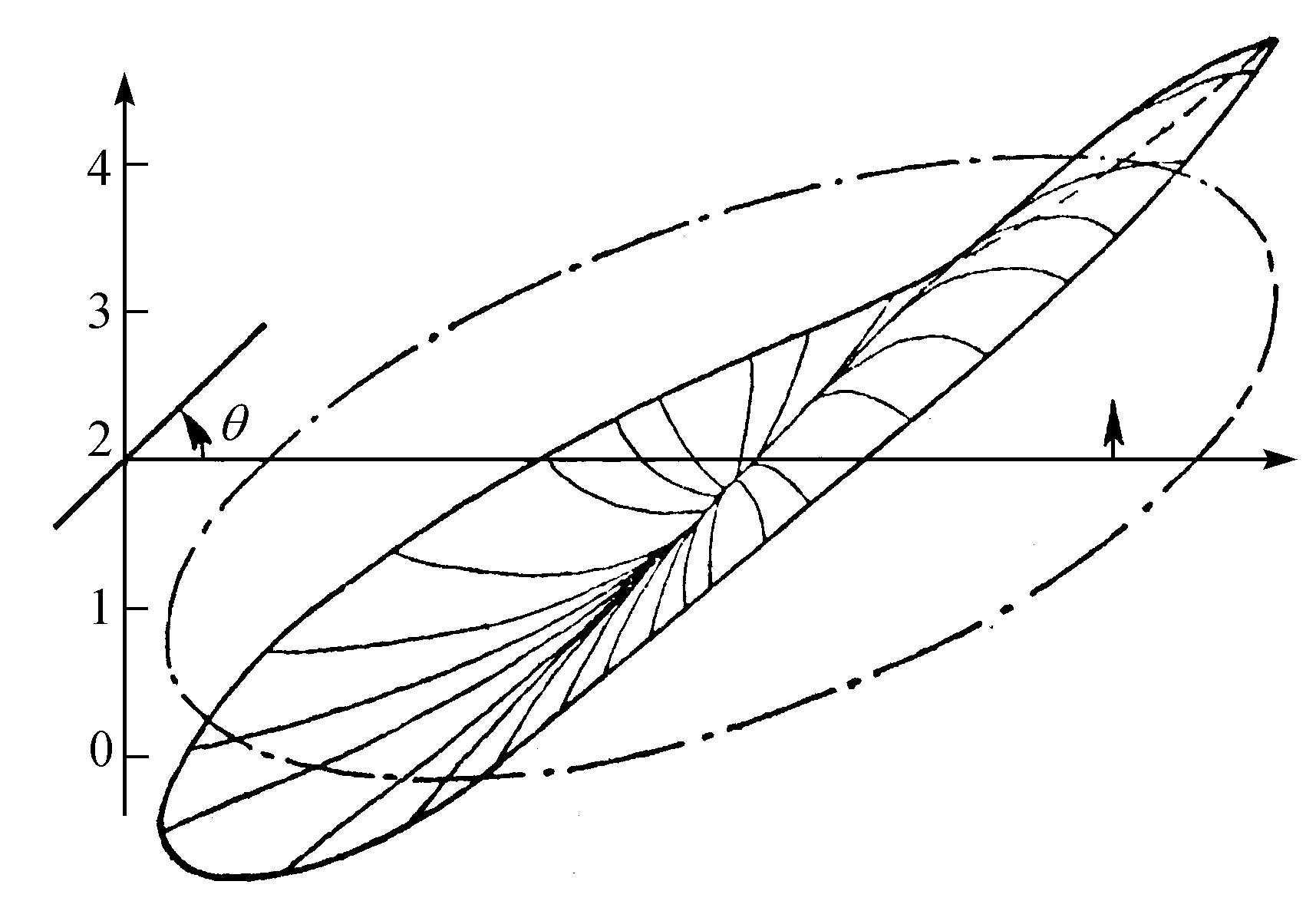
图5.8　二维极化定态耗散结构（由计算机模拟得出）

其参数为：D_x ＝3.25×10^-3 ，D_y ＝1.62×10^-2 ，A＝2，B＝4.6，R＝0.1。

逐级分支可能也是有趣的，例如图5.9所示。在B₀ 之前我们有热力学分支，而在B₀ 处开始了极限环行为。热力学分支仍是不稳定的，不过在B₁ 点分支为两个新解，它们也是不稳定的，但在点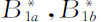 变为稳定的。这两个新解对应于化学波。

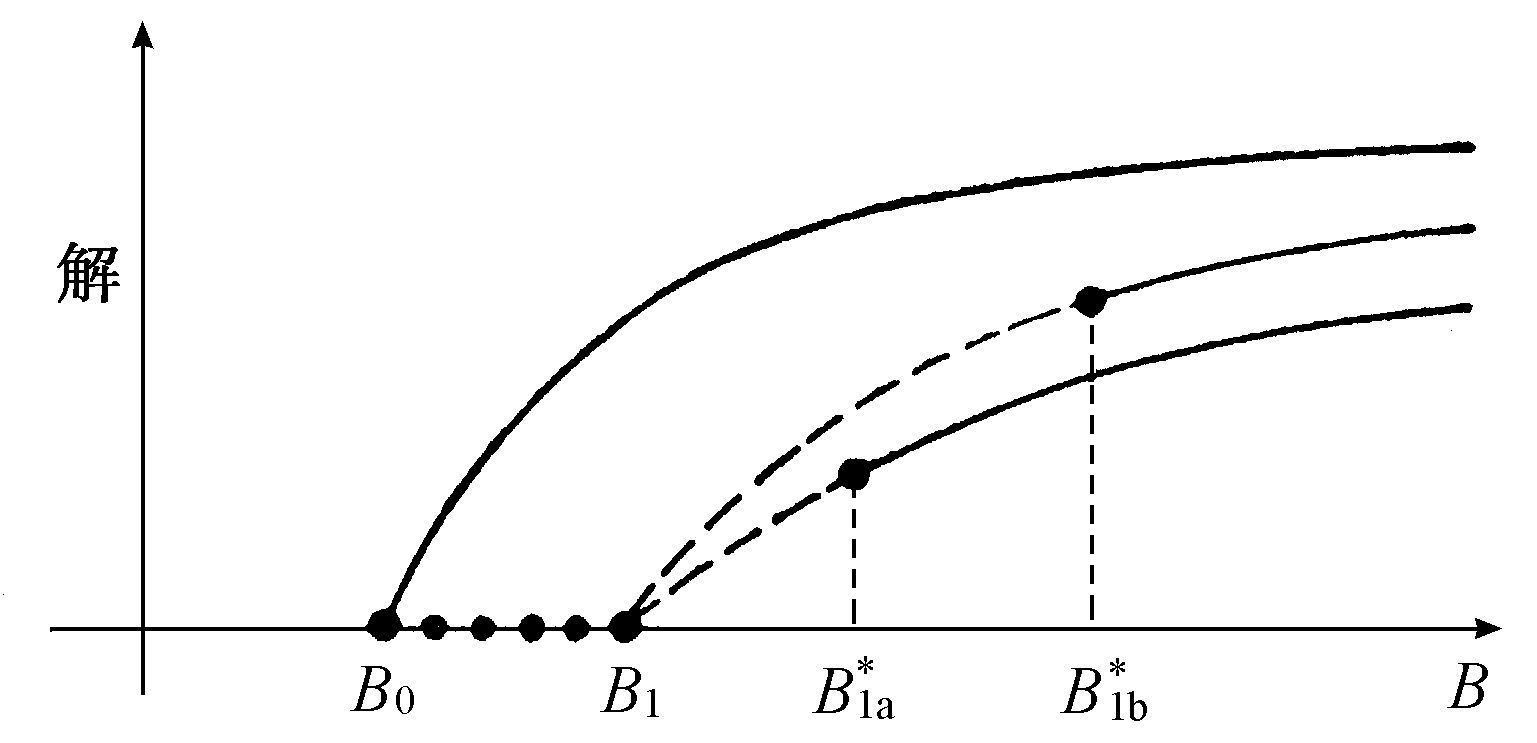
图5.9　引出各种类型波行为的逐级分支

一种类型的波是有一个对称面的波（图5.10），而另一种类型则对应于旋转波（图5.11）。特别值得指出的是，这种情况确实已在化学反应的实验中被观察到了（见本章“化学和生物学中的相干结构”一节）。

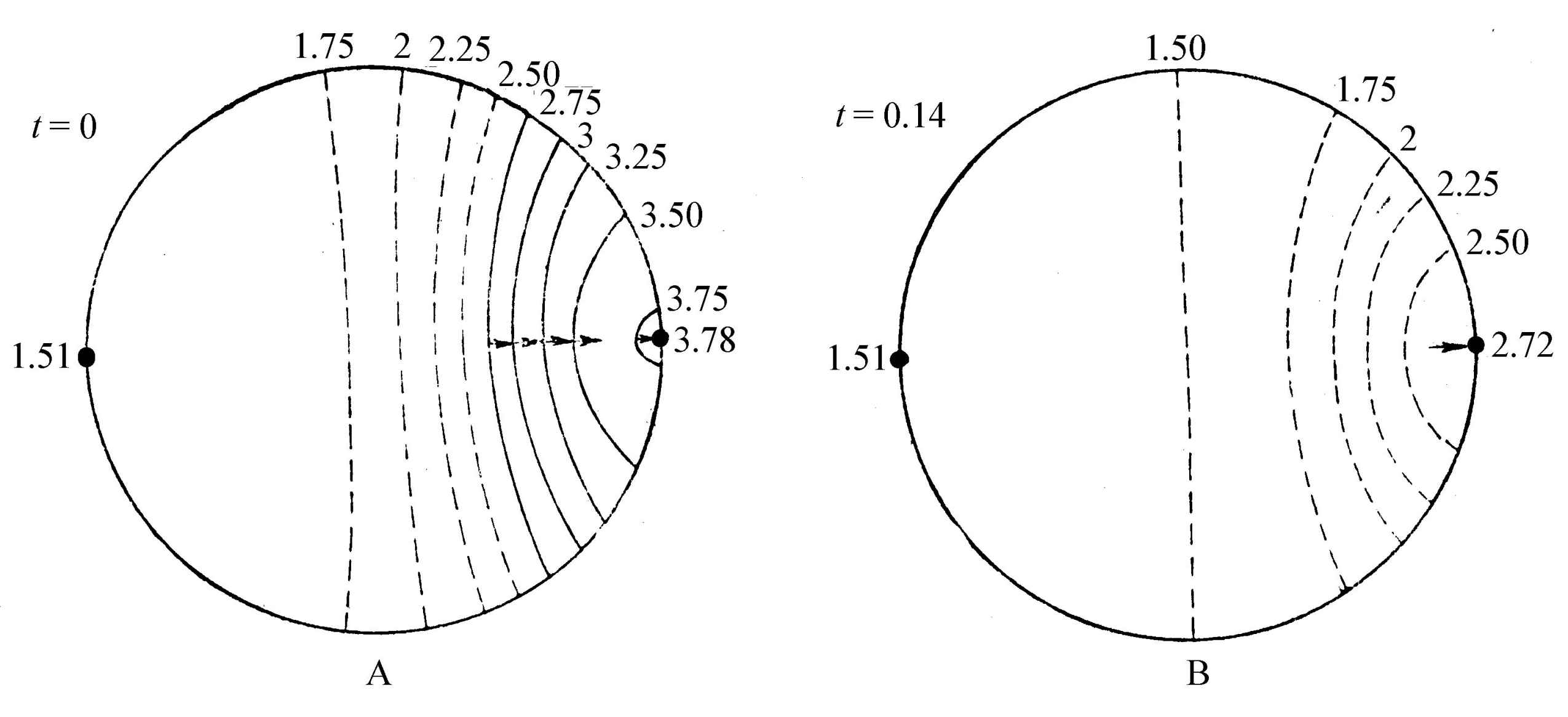
图5.10　三分子模型中X的等浓度曲线

在半径R＝0.5861的圆内，满足零流的边界条件。实线和虚线分别代表浓度大于或小于（不稳的）定态值X₀ ＝2，A＝2，D₁ ＝8×10^-3 ，D₂ ＝4×10^-3 ，B＝5.4。A和B描述周期解的不同阶段上的浓度花纹。

图5.11　三分子模型的旋转解

条件与图5.10相同，但有更大的分支超临界值，即参数B＝5.8。

分支的可解模型

在一个分支之后出现非均匀稳定解的现象是如此出人意料，以至很值得花时间在严格的可解模型中去检验它们的形成（Lefever，Herschkowitz-Kaufman，Turner，1977）。现在我们考虑一个由如下反应模式描述的化学系统：

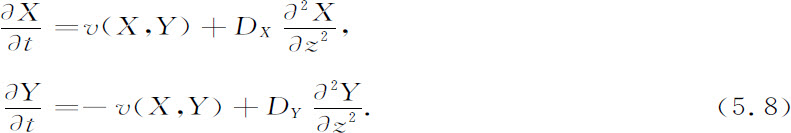
作为例子，我们可以考虑

这是布鲁塞尔器的简化形式，其中式4.57里的反应A→X被略去了。这样的描述出现在涉及膜上酶反应的耗散结构理论中，在膜上，组分X的存在是由扩散保证的，而不是通过“源”A保证的。我们还利用固定的边界条件

这种反应模式的特别简化的特点是存在着一个“守恒量”，这一点可以通过式5.8中两个方程的相加而看出。消去其中的一个变量并积分后，我们得到在定态有效的方程

这里K是积分常数，且

Φ（ω）是ω的某个多项式。这里对它的确切形式不感兴趣，只注意对于ω＝0，有Φ（ω）＝0。十分有趣的是，把这个公式和在方程2.1或2.2中的哈密顿量比较一下，在这里我们把它写成

我们看到，为了从式5.13中的哈密顿量变到方程5.11，我们必须用浓度代替坐标q，而用坐标r代替时间。还要注意，在系统的边界处，ω＝0。

现在让我们考虑两种情况，分别表示在图5.12和图5.13中。如果我们处于图5.12的情况，这时对于ω＝0，Φ（ω）有最大值，只有热力学分支可能稳定。假设我们从ω＝0开始向右，Φ（ω）变为负的，这意味着按照方程5.11，梯度（dω/dr）² 将随离开边界距离的增大而稳定增加。因此我们可以满足第二边界条件。

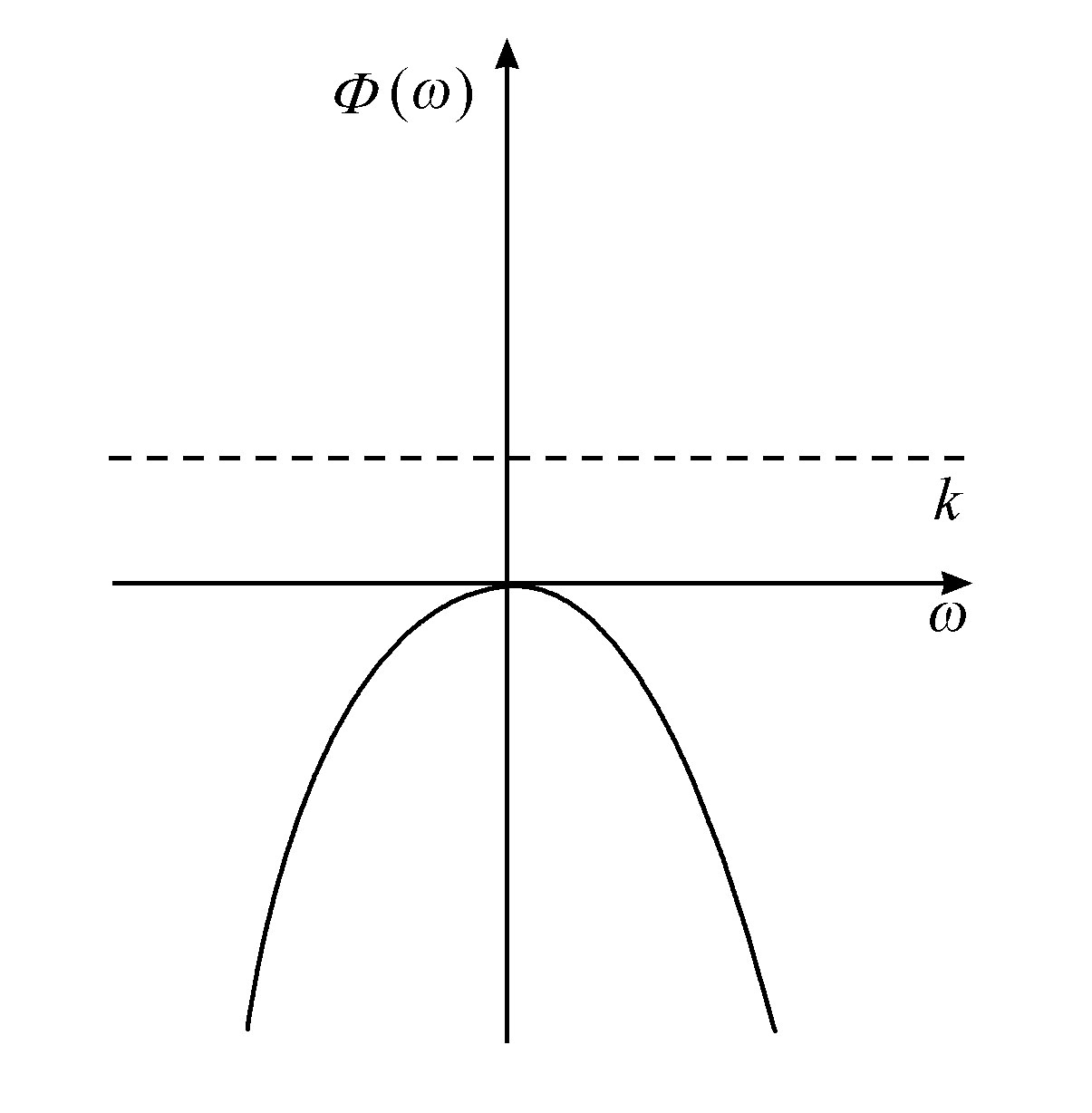
图5.12　相应于没有分支的情况

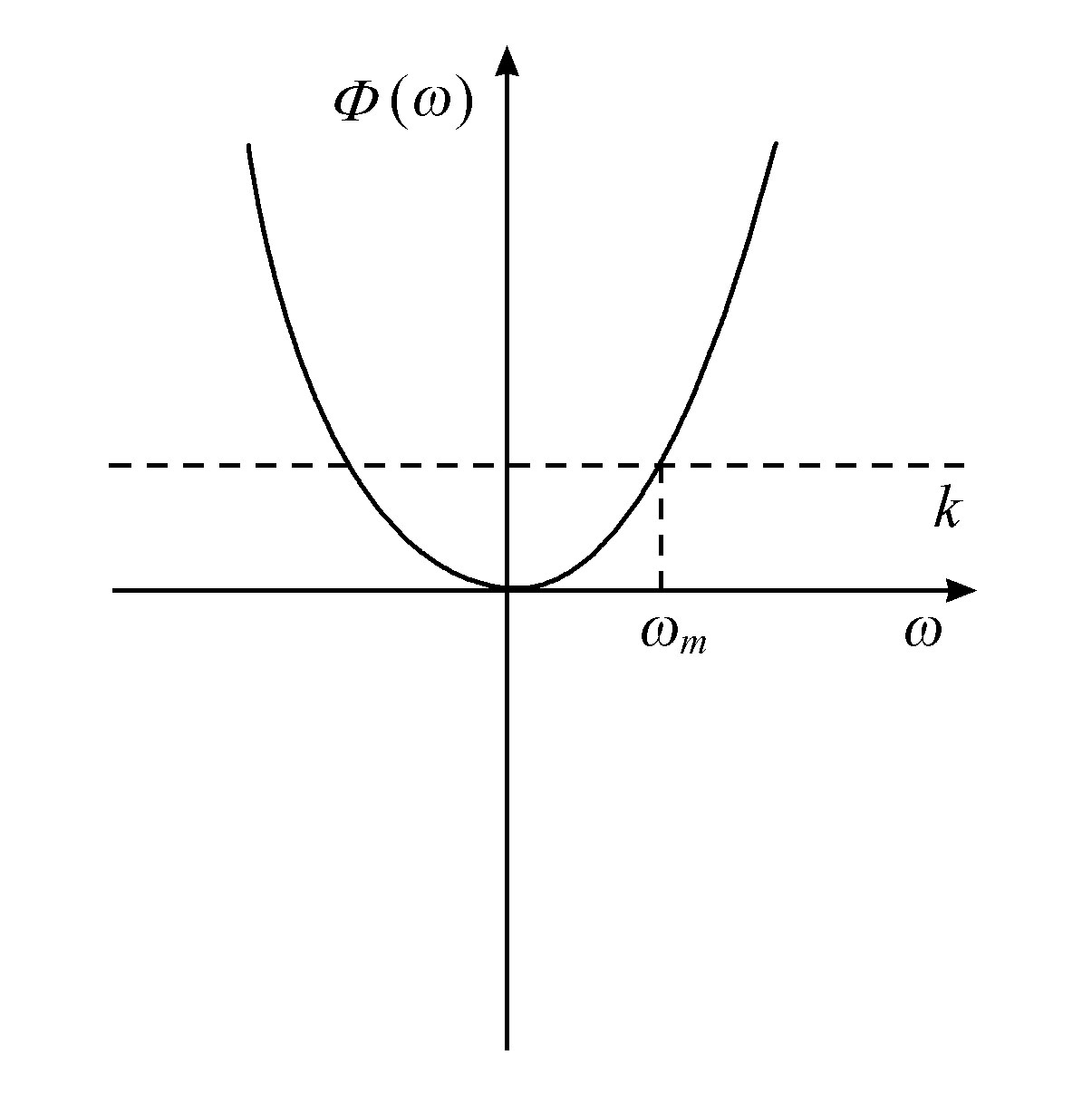
图5.13　相应于分支的情况

当我们考虑对于ω＝0，Φ（ω）有最小值的时候，情况就完全变了。这时我们比方说向右走，就可以一直走到和水平线k的交点。在这个点ω_m 处，梯度dω/dr将为零，因此我们可以用返回到原点ω＝0的方法达到第二边界。这样我们就得到带有单极值的分支解。

显然，其他的更为复杂的解可以用同样的方法建立。我相信，这样就以最简单的方式为我们提供了有效地建立反应扩散系统分支解的办法。有趣的是，经典摆问题中的时间周期性引出了分支解的空间周期性。

如果选择反应空间的特征长度L作为分支参数，就会看到在非线性系统的与时间无关但在空间是非均匀的解同时间周期解之间有着更为引人的类似。结果是，如果L足够小，那么对于自然边界条件，只有空间均匀态存在，而且是稳定的。但是在临界值L_c1 以上，就会出现图5.8所示的那种稳定的单调梯度，并且一直维持到达到第二临界值L′_c1 ，于是，这种花样便消失了（Babloyantz，Hiernaux，1975）。对于空间自组织来说，这个有限长度的存在将和一个有限频率的出现相对照，这个有限频率的出现伴随着如极限环这样的时间周期解的分支（参见刚讨论过的可解模型）。如果L进一步增加，在某个L_c2 处（L_c2 ＞L_c1 ，但有可能＜L′_c1 ），将得到第二花样，它给出一个非单调的浓度剖面。进一步增长还会出现更复杂的浓度花样。它们的相对稳定性将依赖于第二级和更高级分支的发生。

在这个图景中，生长过程和形态学相联系的事实，使人想起早期胚胎发育中形态生成的某些方面。例如繁殖力很强的果蝇（Drosophila），在其蛹的早期发育阶段，“成虫盘”一边生长，一边分到由非常尖锐的边界所分开的小间隔中。这个问题最近由考夫曼及其同事（Kauffman，Shymko，Trabert，1978）用如上所述的在更高长度上多次出现分支的方法进行了分析。

由于存在着第二分支参数L，加上在大多数系统中还存在着动力学分支参数p（图5.2）或B（图5.9），这就使我们能够对空间非均匀耗散结构进行某种系统的（尽管是初步的）分类。如图5.14，分支现象是以单参数描述的，只示出了初级分支后的那些分支。在分支点附近，它们的行为是已经知道的。具体地说，第一分支是稳定的（如果是超临界的，即如果它在p＞p_c1 时出现的话）。其他分支则是不稳定的。更高的分支未示出，因为它们通常在离分支点的有限距离上出现。

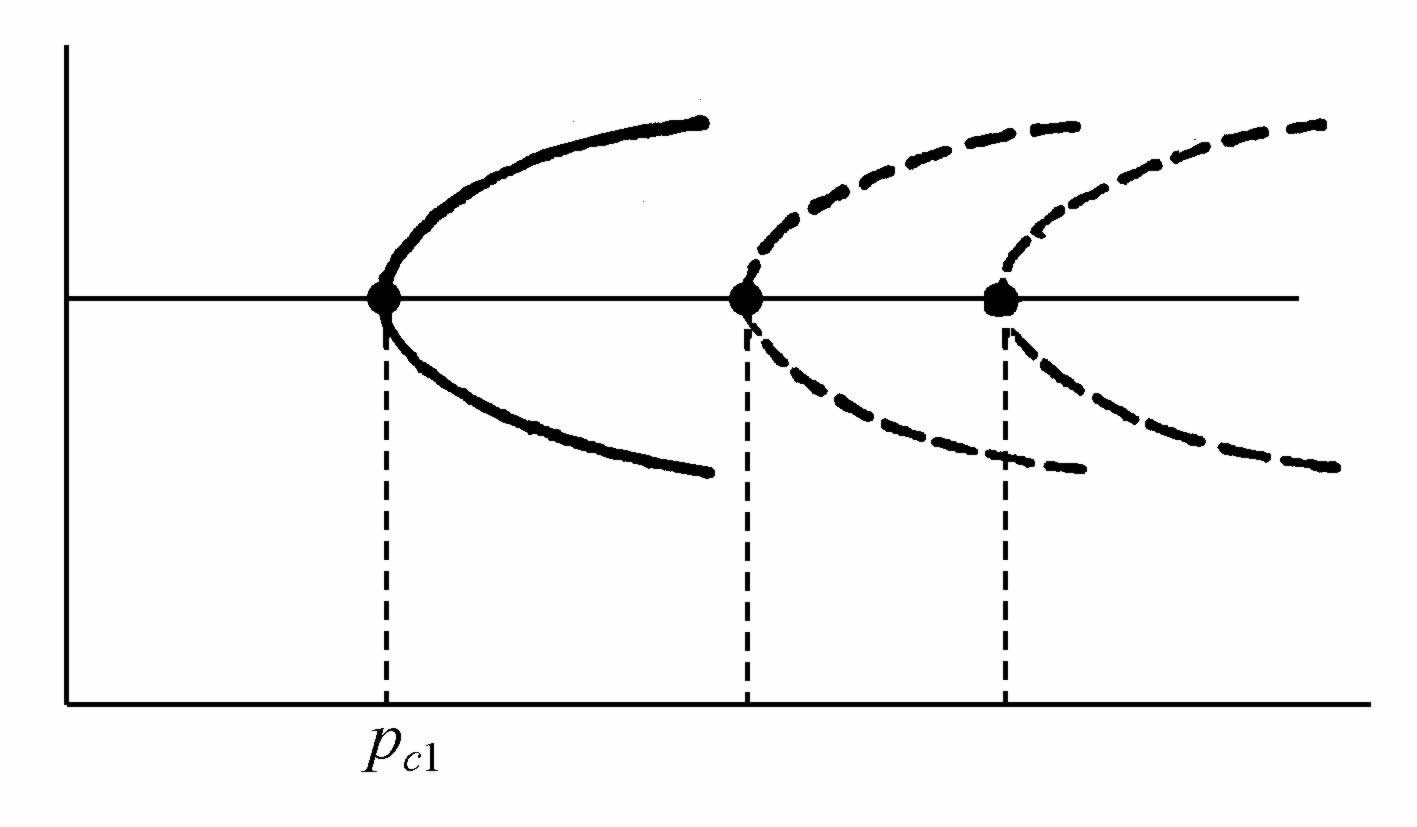
图5.14　从热力学分支得到的逐次初级分支

实线表示稳定分支；虚线表示不稳定分支。

如果在p和L两者的空间中跟踪分支，情况就改变了。对于p与L的一定组合，可能会在线性化算符的倍本征值处出现简并分支，从而分支合并在一起。相反，如果p和L对这种简并状态稍有变化，就能把分支劈开，并可能产生第二级和更高级的分支（Golubitsky，Schaeffer，1979）。问题在于，所有这些可能性都可以进行完全的分类，只要它们仍然靠近简并分支。这种情况开始像突变理论了，虽然一般地说还没有研究从势函数导出的系统。

化学和生物学中的相干结构

1958年，贝洛索夫（Belousov）提出了一个振荡化学反应的报告，这个反应就是在四价铈-三价铈离子对的催化下，溴酸钾氧化柠檬酸。扎鲍廷斯基（Zhabotinski）继续了这一研究（Noyes，Field，1974；Nicolis，Prigogine，1977）。通常，贝洛索夫-扎鲍廷斯基反应需要一个在25℃左右的反应混合物，由溴酸钾、丙二酸或溴丙二酸，以及溶于柠檬酸的硫酸铈（或硫酸铈的某种等效化合物）所组成。这个反应被许多人从实验上和理论上进行了研究。它在实验研究方面所起的作用正和布鲁塞尔器在理论研究方面所起的作用相同。随着条件的改变，各种现象已在很宽的范围内被研究过。例如，观察过均匀混合物中周期的数量级为分钟的振荡现象，还观察过类似波的活性。这个反应的机制，在很大程度上已由诺伊斯及其同事解释清楚（Noyes，Field，1974）。令

是三种关键物质的浓度，而且我们设

那么，诺伊斯机制可以用下列步骤表达：

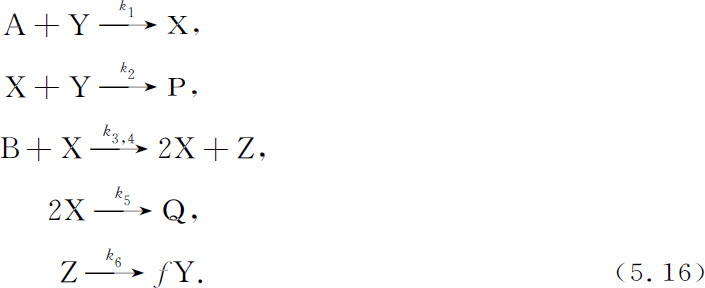
这通常称为俄勒冈器（Oregonator） ⁽¹⁾ 。重要的是，这里存在着交叉催化，比如Y产生X，X产生Z，Z又反过来产生Y，就像在布鲁塞尔器中的情形一样。

许多具有同样类型的其他振荡反应也被研究过了。一个较早的例子是过氧化氢在碘酸-碘氧化偶（即 ）的催化下的分解（Bray，1921；Sharma，Noyes，1976）。最近，布里格斯和劳舍尔（Briggs，Rausher，1973）报告了包括过氧化氢、丙二酸、碘酸钾（KIO₃ ）、硫酸锰（MnSO₄ ）和高氯酸（HClO₄ ）反应的振荡现象，可以看做是贝洛索夫-扎鲍廷斯基和布雷（Bray）反应物的一种“混合”。帕考特（Pacault）及其同事在开放系统的条件下，对这个反应进行了系统的研究（Pacault，de Kepper，Hanusse，1975）。最后，克罗斯（Körös 1978）报告了简单芳香族化合物的一个完整系列（苯、苯胺及其衍生物）和酸性溴酸盐反应，能够在没有金属离子（如铈离子或锰离子）的催化作用的情况下产生振荡现象。而金属离子的催化作用，大家知道，在贝洛索夫-扎鲍廷斯基反应中起着重要作用。虽然在无机化学的领域内振荡反应是极罕见的，但是在生物学有组织作用的各种水平上，从分子水平直到超细胞水平，都已观察到振荡现象。

在最重要的振荡现象里，有一些是代谢振荡，它们和酶的活性有关，它们的振荡周期为分钟的数量级。还有一些是所谓胚胎渐成振荡器（epigenetic osillator），有着数量级为小时的振荡周期。人们了解得最多的代谢振荡的例子是糖酵解循环，它是对于活细胞的力能学最为重要的现象（Goldbeter，Caplan，1976）。这个循环包括一个分子葡萄糖的降解，以及借助一个线性系列的酶催化反应而形成两个分子ATP（三磷酸腺甙）总产量的过程，是酶的活性中的合作效应引起了对振荡反应的催化效应。值得注意的是，在一定的酵解底物注入速率下，链中的一切代谢物浓度都观察到有振荡现象。更值得注意的是，所有酵解的中间产物都以同样的周期但不同的位相进行振荡。酶在反应中的作用有点和光学实验中的尼科耳棱镜一样。它们引起化学振荡中的相移。化学反应的振荡景象在酵解循环中尤为惊人，因为可以从实验上追寻振荡的周期和位相方面各种因素的影响。

胚胎渐成类型的振荡反应也是众所周知的。它们是在细胞水平上的调节过程的结果，蛋白质通常是稳定分子，而催化反应是非常快的过程。一个细胞里蛋白质的水平趋于过高的情况并非是不寻常的。于是，有机体使用某些物质来抑制大分子的合成，这种反馈就引起振荡。这种现象已被仔细地研究过，例如大肠杆菌中乳糖操纵子的调节作用。还可以援引许多其他例子，比如粘菌中的群集过程，含有膜边界处的酶的反应等等。感兴趣的读者可参看有关文献（请查Nicolis，Prigogine，1977）。

看来，几乎所有的生物活动都包括某些机制，这些机制表明生命中含有超出热力学分支稳定性阈值的、远离平衡态的条件。因此，它诱使人们猜想，生命的起源可能和逐级不稳定性有关，这和引起相干性不断增加的物态的逐级分支有些类似。

贝洛索夫-扎鲍廷斯基反应：化学卷曲波

当贝洛索夫-扎鲍廷斯基反应物被放在浅盘中时，显现出螺旋状的化学波。该波可以自发地出现，也可用使其表面与热灯丝接触的方法启动，如上面照片中的那样。其中那个小圆圈是该反应所演化出的二氧化碳的泡。

这组连续照片依次在第一张照片拍摄后的0.5，1.0，1.5.3.5，4.5，5.5，6.5和8.0秒时拍摄。

生　态　学

现在让我们讨论稳定性理论可应用于结构稳定性的一些方面（Prigogine，Herman，Allen，1977）。我们考虑一个简单的例子。群体X在给定培养基中的生长通常可用下式表达：

其中K和出生率有关，d和死亡率有关，N是供养该群体的环境容量的量度。方程5.17的解可以借助于图5.15中的逻辑曲线（logistic curve）来表示。

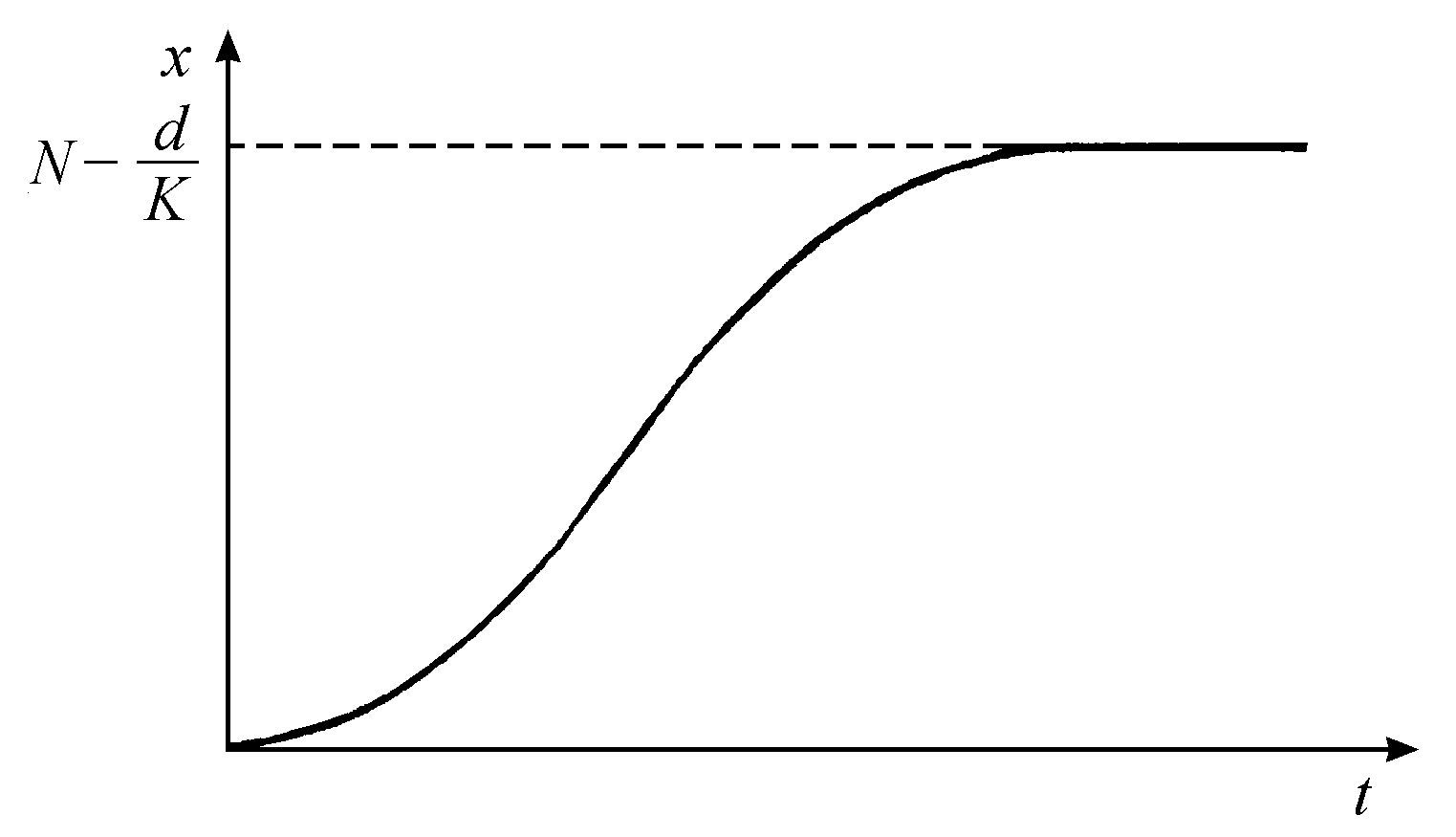
图5.15　逻辑曲线

这个进化完全是决定论的。即当环境被饱和时，群体就停止增长。但是在该模型所不能控制的事件发生后，也可能在同一环境中出现新的物种（具有另外的生态参数K，N和d），它们起初数量很少。这是一种生态涨落，它引起结构稳定性的问题：这个新的物种或者可能消失，或者可能取代原来的物种。利用线性稳定性的分析很容易证明，仅当满足

时，新物种才能取代原来的物种。假定物种对所谓生态小生境的占据取如图5.16所示的形式。

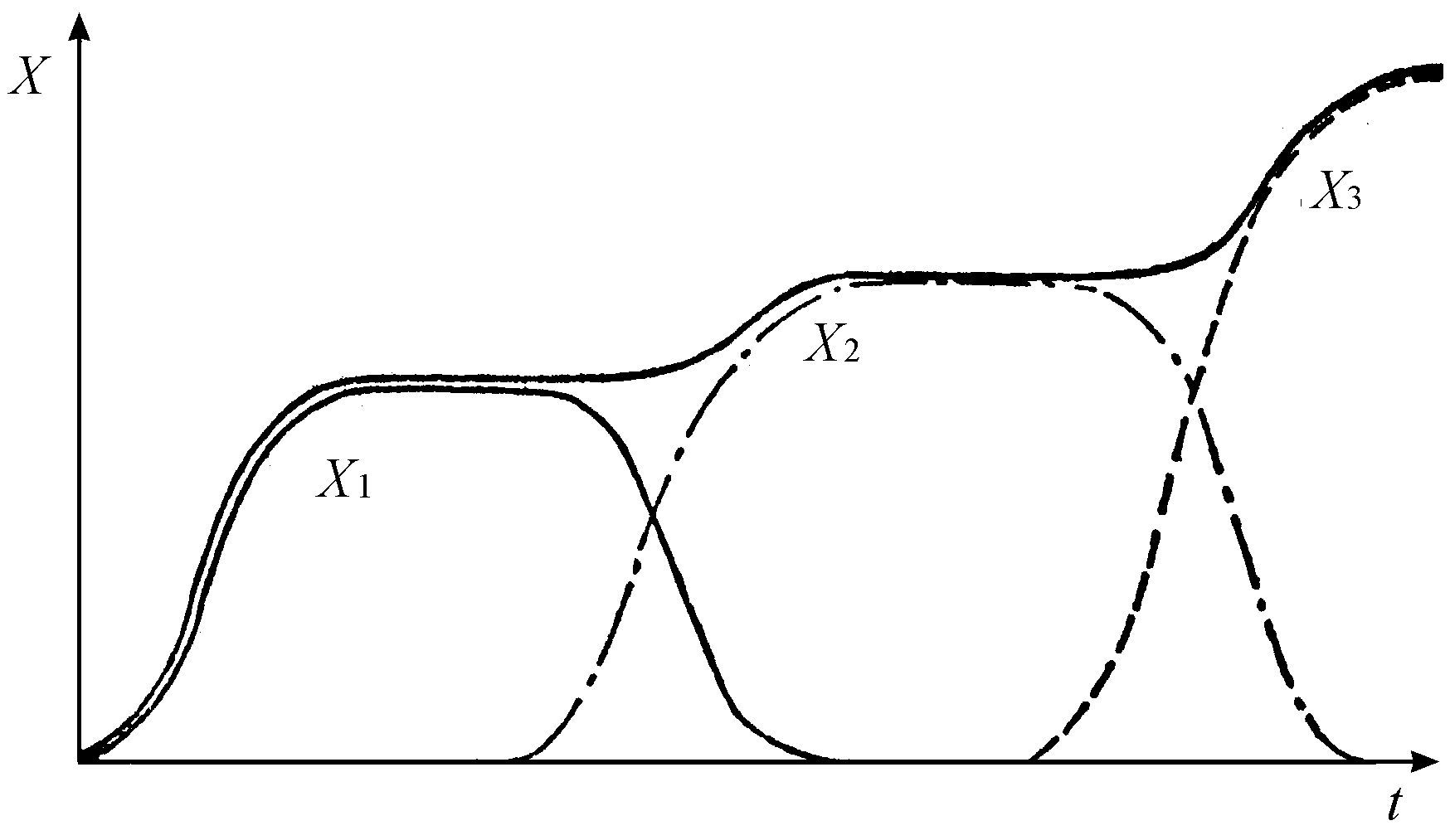
图5.16　生态小生境被后继物种占据

这个模型定量地描述了“适者生存”原理在开发某个给定的生态小生境问题中的意义。

考虑到群体为其生存下来而使用的各种可能的策略，就可以引入各种各样的这类模型。例如，我们可以区分食用多品种食物的物种（所谓“多面手”）以及其他的食物范围很窄的物种（所谓“专门家”）。我们也可以考虑这样的事实，即某些群体固定其群集的一部分用于“非生产性”职能，例如“士兵”。这和昆虫的群居多态性密切相关。

还可以把结构稳定性和通过涨落达到有序的概念用于更复杂的问题中，而且甚至可以用来极为粗略地研究人类的进化。作为一个例子，我们从这种观点考虑都市进化的问题（Allen，1977）。用逻辑方程5.17来说，都市区域的特点在于它的容量N随着经济职能的增加而增加。令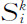 表示在点i（比如说“城市”是i）的第k种经济职能。于是我们得到取代式5.17的如下形式方程：

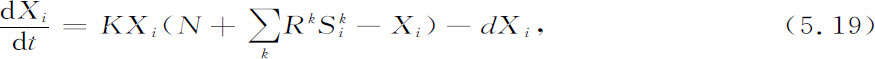
其中R^k 是比例系数。不过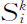， 本身伴随人口X_i 的增长是以复杂的方式进行的：它起着自催化作用，但这个自催化的速率取决于在点i对于职能 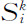所提供的产品k的需求量（来自某个区域的需求量受到随着对i的距离而增加的运输费用的限制），以及和位于另一点的对手单位的竞争。

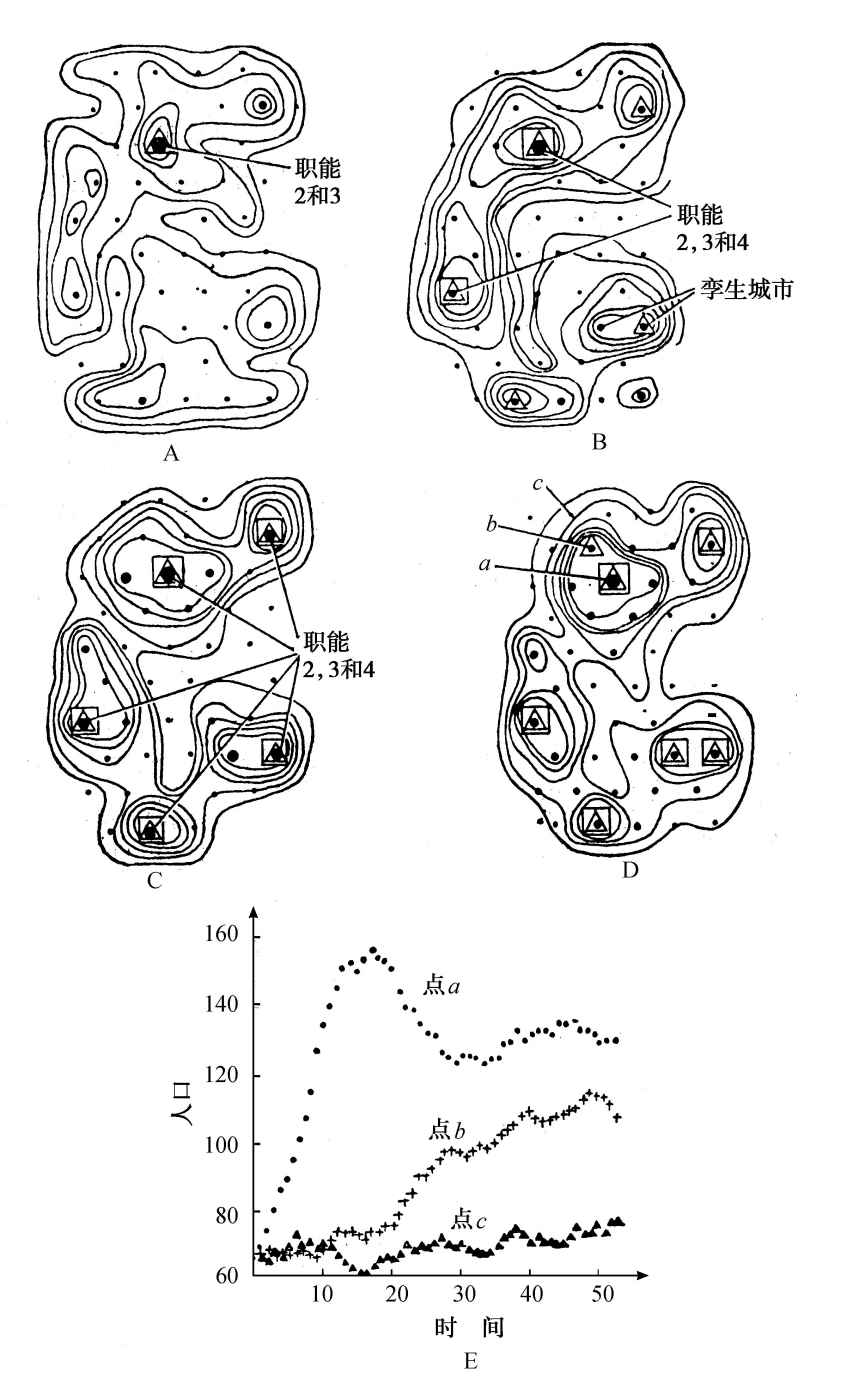
图5.17　都市化的一种可能的“历史”

在这个地区上，最初具有均匀的人口。把这个地区分为50个小区域，组成一个网络。在每个网点上可以看到四种经济职能，在一个随机的时间序列中，各种各样的企图一个接着一个地发生。

A 在时间t＝4时，50个点的格阵上的人口分布。在t＝0时，每个点的人口是67。

B 在t＝12时，正在出现基本的都市结构，该地区具有5个人口迅速增长的中心。

C 到了t＝20时，都市结构已经巩固，并且最大的中心显示了在市郊住宅区出现的“都市延伸”。

D 在t＝34时，都市中心增长缓慢，而在都市之间的地带出现“平均值以上的增长”，其结果是削弱都市化。

E 在图D中标明的点a，b和c上，人口在整个模拟过程中的增长。

在这个模型中，一个经济职能的出现可以比作一个涨落。这个经济职能的出现将通过开创就业机会从而使人口集中于一点的方法打破人口分布的初始均匀性。为了维持下去，就业机会将使相邻一些点的要求枯竭。当介入已经都市化了的区域时，它们可能会被类似的然而发展得更好或更为合适的经济职能的竞争所挤垮；它们也可能在共存中发展；或者以这些经济职能中的一种或另一种的毁灭为代价而发展。

图5.17说明了初始均匀区域都市化的一种可能的历史，在该区域中，可以在50个地点的网络中的每个点上找到四种经济职能的发展，各种尝试在一个随机的暂时序列中彼此追逐。最终结果以复杂的方式依赖于决定论的经济法则和随机的涨落演替之间的相互作用。任何一个特殊模拟的细节都和该区域的精确“历史”有关，因此我们只粗略地考虑结构形成的一定的平均性质。例如，对于虽经历了不同历史但具有同样参数值的系统来说，大中心的数目以及平均间隔是近似相同的。这样的模型可以用来估计较长时期的有关运输、投资等决策的后果，因为这些活动经历了该系统的各个相互作用环节，而且发生了不同经理人员先后所作的调整。一般地说，我们看到由于系统的许多经营者所起的作用（选择），由于至少部分地具有评价这些作用（有用的职能）的互相依赖的判据，这样的模型为理解“结构”问题提供了一个新的基础。

结　　语

上节中所研究的几个例子已经把我们引到了距离经典力学和量子力学简单系统相当远的地方。我们应注意，结构的稳定性是没有限制的，只要引入合适的扰动，任何系统都可以呈现不稳定性。因此，不会有历史的终点。马格列夫在其出色的讨论中指出了所谓“自然世界的巴罗克” ⁽²⁾ （Margalef，1976）。他的意思是说，生态系统所包括的物种比单纯把生物学效能作为组织原则时所“必须”有的物种要多得多。这个自然界的“超创造力”当然出自我们这里所提出的描述模式，“变异”和“创新”随机地发生，而且被瞬间奏效的决定论关系归集到系统之中。因此，在这种看法下，我们得到“新类型”和“新思想”的不断产生，它们可以纳入系统结构中去，引起系统结构的不断进化。

————————————————————

(1) 因诺伊斯等是在美国俄勒冈（Oregon）大学研究此问题而得名。——译者注。

(2) 巴罗克（baroque）指建筑或艺术上的一种风格，其特点是过于雕琢和怪诞。——译者注。