第七章　根据公理Ⅰ～Ⅳ的几何作图

Chapter VII. Geometric Constructions Based on Axioms I～IV

§36　利用直尺和迁线器 ^（1） 的几何作图

设有一种空间几何，在这几何中全体公理Ⅰ～Ⅳ都成立；为简单起见，我们在本章中只考虑这空间几何中的平面 几何，研究这平面几何中哪些初等作图问题一定能够解决（假设有适当的实际工具）。

根据公理Ⅰ，Ⅱ，Ⅳ，恒能够解决下述问题：

问题1 　作一直线连结两点；求非平行的两直线的交点。

根据合同公理Ⅲ，能够迁移线段和角，即在我们的几何中恒能够解决下列问题：

问题2 　迁移一给定的线段到一直线上的一给定的点处，并且在这点的给定的一侧。

问题3 　迁移一给定的角，到沿着一给定的直线，以这直线上的一给定点作顶点，并且在这直线的给定的一侧，或者作一直线，交一给定的直线于一给定的点，并且交于一给定的角。

显然，在用公理Ⅰ～Ⅳ作根据时，只有那些可化为上述问题1～3的作图问题才能够解决。

在基本的问题1～3之外，我们再增添下列两个问题：

问题4 　作一直线通过一给定的点，平行于一给定的直线。

问题5 　作一给定的直线的垂线。

我们立刻知道，这两个问题能够用不同的方式化为问题1～3。

问题1的实际作图需要直尺 。为了问题2～5的实际作图，如同下面将要证明的，直尺之外还需要应用迁线器 ；迁线器是一个工具，它能够迁移唯一的一条完全确定了的线段 ^（2） ，例如单位线段。因此有下述结果：

定理63 　根据公理I～Ⅳ所能解决的几何作图问题，一定可以利用直尺和迁线器实际作图。

证明 　要实际解决问题4（图78），连接这给定的点P 和给定的直线a 上的任意一点A ，而且用迁线器继续两次迁移单位线段到a 上的点A 处，先到点B ，再从B 到C 。再设D 是AP 上任意一点，但既非A 又非P ，而且使得BD 不平行于PC 。因而CP 和BD 交于一点E ，而且AE 和CD 交于一点F 。如同施泰因纳尔（Steiner）曾经指出的^【74】 ，PF 就是所求的a 的平行线。

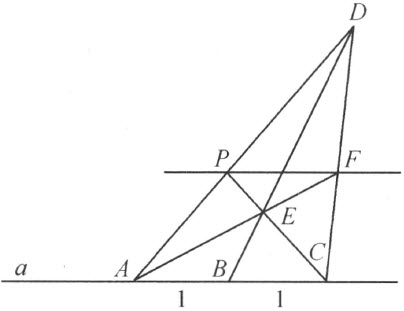
图　78

我们解决问题5如下（图79）：设A 是给定的直线上的任意一点；然后用迁线器迁移单位线段到这直线上的点A 的两侧，得到AB 和AC ；再在通过A 的任意另外两条直线上决定点E 和D ，使得线段AD 和AE 也等于单位线段。直线BD 和CE 交于一点F ，直线BE 和CD 交于一点H ，则FH 是所求的垂线。事实上：角∠BDC 和∠BEC 都是在直径BC 上的半圆的圆周角，因而都是直角；把三角形的三高线共点的定理应用到三角形BCF ，得知FH 也垂直于BC 。

图　79

根据问题4和问题5，恒能够从给定的直线a 外的给定的点D ，作a 的垂线，或者通过a 上的一点A ，作a 的垂线。

现在能够只用直尺和迁线器解决问题3；我们采取下述方法，这方法只需要作给定的直线的平行线和垂线：设β 是要迁移的角（图80），A 是这个角的顶点。通过A ，作直线l 平行于给定的直线，即给定的角β 要迁移到的直线。从β 的两边的任意一边上的任意一点B ，作到β 的另一边和到l 的两条垂线。设这两条垂线的垂足是D 和C ，C 和D 不是同一点，而且A 不在CD 上。能从A 作CD 的垂线；设垂足是E 。根据本书所证明的定理，∠CAE ＝β 。若B 是取在给定的角的另一边上，E 就落在l 的另一侧。通过给定的直线上的给定的点，作AE 的平行线；于是问题3解决了。

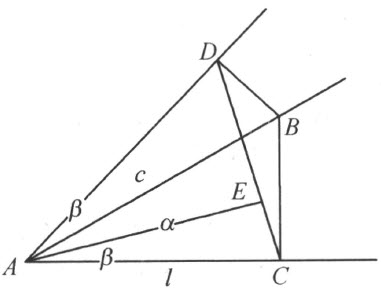
图　80

最后，要解决问题2，我们用下述的，魁尔夏克（J，Kürschák）所给的简单作图法：设AB 是要迁移的线段（图81），而且P 是给定的直线l 上的给定的点。通过P 作AB 的平行线，用迁线器迁移单位线段到这平行线上的点尸处，在AP 的B 侧，到一点C ；再迁移单位线段到l 上的点P 处，在给定的那一侧，到一点D 。通过B 作AP 的平行线，交直线PC 于Q ，通过Q 作CD 的平行线，交l 于E ：则PE ＝AB 。若l 和直线PQ 重合，而且Q 不在P 的那给定的一侧，作图法能够容易修正。

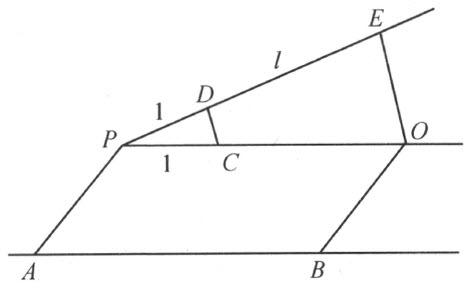
图　81

如是证明了，问题1～5全体能用直尺和迁线器解决，从而定理63完全证明了。

§37　几何作图能否用直尺和迁线器作出的准则

在§36中所处理的初等几何问题之外，还有一系列很多的其他问题，它们的解决也只需要作直线和迁移线段。要想对于所有的能如此解决的问题有一个概括的了解，我们用一个直角坐标系作我们以后讨论的基础，而且，如同通常一样的，把点的坐标看做是实数或者某些任意参数的函数。要想能够求得全体能作图的点，我们作如下的考虑：

设给定了一组确定的点；这些点的坐标产生一个有理域R ^【75】 ，它含有某些实数和某些任意参数P 。再设想从给定的这组点，通过作直线和迁移线段所能作的全体点。把这些点的坐标所作成的域叫做Q （R ）；它也含有某些实数和这些任意参数P 的某些函数。

我们在§17中的讨论表明：直线和平行线的作图可以解析地化为线段的加乘减除；再者，已知的§9中给出的旋转的公式告诉我们，迁移一线段到任意一直线上所需要的解析运算，只是求两个平方的和的平方根，而这两个平方的底是已经作出来了的。反过来，根据毕达哥拉斯定理，利用一个直角三角形，我们恒能够通过迁移线段作出两个线段的平方的和的平方根。

从这些考虑就得到，域Q （R ）所含有的实数和参数P 的函数，是而且只是那些从R 中的实数和参数的函数，经过有限次下列五种运算所产生的；四种初等运算和求两个平方的和的平方根这五种运算。这些结果叙述如下：

定理64 　一个几何作图问题能通过作直线和迁移线段解决，即能利用直尺和迁线器解决，其充分必要条件如下：在用解析方法处理这问题时，所求的点的坐标是给定点的坐标的这样的函数，它们的建立只需要有理运算和求两个平方的和的平方根这个运算，而且只需要应用有限次的这五种运算。

从这定理立刻知道，不是每一个用圆规能解决的问题也能只用直尺和迁线器解决。为此，我们从§9中利用代数数域Q 所建立的那种几何出发；在这几何中只有能用直尺和迁线器作出的线段，即由域Q 的数所决定的线段。

设ω 是Q 中的任意一个数，从域Q 的定义，很容易知道，每一个和ω共轭的代数数必定也在Q 中；而且，既然域Q 中的数都显然是实数，所以域Q 只能含有完全实数^【76】 ；所谓完全实数，指的是只有实共轭数的实代数数。

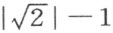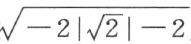现在，我们提出下述问题：作一个直角三角形，其弦是1而且一股是 。表出另一股的数值是代数 ；它不在Q 中出现，因为它的共轭数 成为虚数。如是所提出的问题在我们据以出发的几何中不能解决，从而也不能用直尺和迁线器解决，虽然它是可以利用圆规立刻解决的。

我们的考虑也可以反转过来，即有：

自有理数经过实平方根所得的每一个完全实数都在域Q 中，因此每一条由这样的数所决定的线段都能够利用直尺和迁线器作出 ^（3） 。这定理的证明将从更普遍的考虑得来。实际上我们将要找出一个准则，使对于一个能用直尺和圆规解决的几何作图问题，能直接从这问题的解析性质和它的解来判断它是否也能只用直尺和迁线器来解决。下述定理就提供给我们这个准则：

定理65 　设有一个几何作图问题，在解析的处理时，其中所求的点的坐标，只要通过有理运算和开平方，就能从给定的点的坐标求出。设n 是足够用来计算点的坐标的平方根的最少个数。我们的作图问题可以只经过作直线和迁移线段实际解决的充分必要条件如下：对于给定的点的所有 的位置，即对于作为任意参数的给定的点的坐标的所有 的值，这个几何问题恰好有2ⁿ 个实解 ^（4） ，无穷解也计算在内。

根据本节开始时的考虑，所说的准则的必要性显然。至于准则的充分性，由于下述的定理：

定理66 　设参数P ₁ ，…，P _n 的一个函数f （P ₁ ，…，P _n ）是经过有理运算和开平方而作成的。若对于参数的每一组 实数值，这函数都是一个完全实数 ，则这函数属于域Q （R ）。这里的域是从1，P ₁ ，…，P _n 出发，经过初等运算和两个平方的和 的开平方而得到的。

先注意：在域Q （R ）的定义中，只 取两个 平方的这个限制可以去掉。事实上，公式

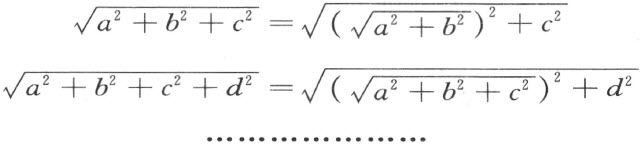
表明任意多个平方的和的开平方可以化为继续两个平方的和的开平方。

因此，设一个有理数域是由逐次附加在函数f （P ₁ ，…，P _n ）的构造中每次居于最里面的平方根扩张而成的。在考虑这种的一个有理数域时，只需要证明，这些平方根的每一个的被开方数，在前一个有理数域中都可以表为平方和，这个证明根据于下述的代数定理：

定理67 　若一个以有理数为系数的有理函数ρ （P ₁ ，…，P _n ），对于参数的所有的实值，都取非负值，它就可以表成以有理数为系数的、变数P ₁ ，…，P _n 的有理函数的平方的和 ^（5） 。

我们把这条定理述成下式：

定理68 　在由1，P ₁ ，…，P _n 决定的有理数域中，每一个永远非负（对于变数的每一组实数值都非负）的函数是一个平方和。

现在设有一个函数f （P ₁ ，…，P _n ），它具有定理66中所说的性质。附加构造函数f 所必需的平方根，逐步地作扩张，就得到一个域。我们能推广上述的论断，使得它在这域中成立。即对于这个域有下述事实。若一个函数和它的所有的共轭函数都永远非负，它就可以表为这域中的函数的平方和。

用数学归纳法证明。首先考虑经过附加f 中的最里面的一个平方根扩张R 而成的一个域。这个平方根的被开方数是一个有理函数 f ₁ （P ₁ ，…，P _n ）。设f ₂ （P ₁ ，…，P _n ）是经过这个扩展而成的域（R 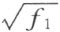， ）中的一个函数，它和它的所有的共轭函数都只取非负值，而且它不恒等于零；它有 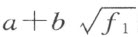的形式，其中的a 和b 以及f ₁ 都是有理函数。从关于f ₁ 所作的假设，可知函数 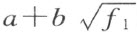和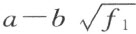 的和φ与积ψ都只取非负值。函数

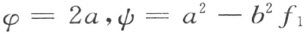
还是有理的，所以根据定理68可以表为R 中的函数的平方和。此外，φ 不能恒等于零。

从f ₂ 所满足的方程

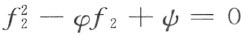
得到

根据关于φ 和ψ 所说的，所以f ₂ 可以表为域（R 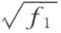， ）中的函数的平方和。这里对于域（R 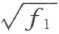， ）所得到的结果相当于对于域R 而言的定理68。对于其余的扩张，重复上面应用的步骤，我们最后得到下述结果：在作成函数f 所得到的诸域的每一个中，若一个函数和它的所有的共轭函数都永远非负，则它就是从对应域中取的函数的平方和。现在考虑任意一个在f 中出现的平方根式，它和它的所有共轭函数应该都是实的，所以被开方式以及它的所有的共轭式，在它所在的域中，应该都是永远非负的函数，因此这个被开方式是这域中的平方和。因此定理66证明了；所以，定理65所给出的准则也是充分的。

能用直尺和圆规作图的正多边形是定理65的应用的例子。在这情形下，没有任意参数p 出现，所要作的式子都是代数数。我们容易看出，定理65的准则满足了^【77】 ，因此，只通过作直线和迁移线段，就能做出每一个正多边形。这个结果也可以从圆周等分理论直接得到。

其他有关初等几何中的已知的作图问题，这里我们只提马耳发提（MaLfatti）问题^【78】 能只用直尺和迁线器解决，而亚波隆尼亚（Apollonius）相切问题^【79】 则不能 ^（6） 。

————————————————————

（1） 希尔伯特在配合他的公理系统作图时设计一个作图工具，他将这个工具叫“ ”。1902年美国人汤森德（E. J. Townsend）将第一版德文原著译成英文时，根据此字的意义译为“Transferer Of segments”。今根据此英译名词译作“迁线器”。——译者注

（2） 只需要要求能够迁移唯一 的一条线段，是魁尔夏克（J.Kürɜchák）注意到的；参看他的“线段的迁移”（Das　Strechenabtragen，Math．Ann．卷55。1902）。

（3） 此处在第七版中所出现的错误系由巴赫曼所指出。

（4） 此处参看补篇Ⅳ₂ 。

（5） 在一个 变数时，我最先讨论这个问题，然后兰道（E．Landau）完成了对于一个变数的这条定理的证明，而且用的是很简单的和初等的工具，Math. Ann. 卷57，1903。近来阿廷丁（Artin）得到了完全的证明，Hamburger Abhandlungen，卷5，1927。

（6） 关于其他用直尺和迁线器的几何作图问题，参看M. FEldblum。“关于初等几何作图”，就职论文，Göttingin，1899。