第二章 热运动方程
·Chapter II Equations of the Movement of Heat·
傅立叶导出的热传导方程及其求解过程中使用的变量分离法已成为现代偏微分方程基础理论的重要组成部分;傅立叶积分也是用封闭形式解偏微分方程的主要方法。这一思想在他1811年的获奖论文中已体现出来,后来又在1822年的专著中总结了如何用这个积分求解各种类型的微分方程;傅立叶工作的另一重要影响是促进了数学中的函数概念及有关概念的发展。

在荣纳河东岸所看到的让欧塞尔人引以自豪的圣·热尔曼修道院全景
第一节 环中变化的热运动方程
101 我们可以建立表示任一形状的固体物质中热运动的一般方程,并把它们应用到特殊情况中去。不过,这种方法常常会涉及很复杂的计算,这种计算不难避免。有几个问题我们最好以表示适合于它们的条件的特殊方法来处理;我们现在就采取这一步骤,并分别考察导言第一节所阐明的问题。开始我们只局限于建立微分方程,随后几章将给出它们的积分。
102 我们已经考虑过一端浸入一个恒定热源的细棱柱棒中的均匀热运动。这第一种情况不会有任何困难,因为除了温度的永恒状态外不涉及别的任何问题,表示它们的方程不难积分。下面的问题则需要更深入的研究;它的目的是要确定其不同的点已经得到完全任意的初始温度的一个固体环的变化状态。
这个固体环或臂环由一个矩形截面绕一个垂直于环平面的轴旋转而成(见图3),l是面积为S的这个截面的周长,系数h计量外热导率,K计量内热导率,C是比热,D是密度。曲线oxx′x″表示这个臂环的中周,或者是表示通过所有这些截面图形中心的那条曲线。一个截面与原点的距离由长为x的弧所测定;R是中周的半径。
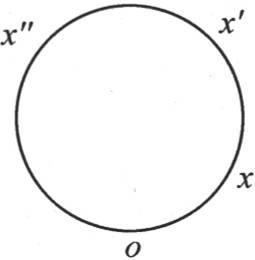
图3
假定鉴于这个截面的微小面积和形状,我们可以认为同一截面不同点的温度相等。
103 设想这个臂环的不同截面的任意初始温度已经给定,然后这个固体受保持0度且以定速移动的空气的作用;这个温度系统将不断变化,热将在这个环中传导,并在表面耗散:需要的是确定这个固体在任一给定时刻的状态。
设v是距离为x的截面在历经时间t后所获得的温度;v是x和t的某个函数,所有初始温度也应当进入该函数中:这就是待求的函数。
104 我们要考虑在由一个距离为x的截面和另一个距离为x+dx的截面之间所围成的一个无穷小薄片中的热运动。对某一时刻的长度来说,这个薄片的状态就是由保持不等温的两个平行平面所限定的一个无穷固体的状态;因此,根据导言中所建立的原理,在这个时刻dt内过第一个截面、并由此从这个薄片前面的这个固体的部分进入这个薄片本身的热量,由四个因子的积来计算,即由热导率K,截面面积S,比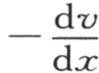 和时刻长度的积来计算,其表达式是
和时刻长度的积来计算,其表达式是 为确定从这同一薄片过第二个截面所逃逸、并进入这个固体毗邻部分的热量,只需在前一表达式中把x变成x+dx,或者同样地,把它对x的微分加到这个表达式中就够了;因此,这个薄片通过它的第一个面所得到的热量等于
为确定从这同一薄片过第二个截面所逃逸、并进入这个固体毗邻部分的热量,只需在前一表达式中把x变成x+dx,或者同样地,把它对x的微分加到这个表达式中就够了;因此,这个薄片通过它的第一个面所得到的热量等于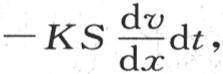 过相对的面所失去的热量由
过相对的面所失去的热量由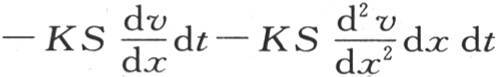 来表示。因此,由于这个薄片的位置,它得到等于前两个量的差的热量,即
来表示。因此,由于这个薄片的位置,它得到等于前两个量的差的热量,即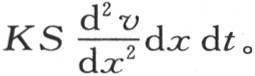
另一方面,外表面为ldx,温度与v相差无穷小的这同一薄片,允许等于hlv dx dt的热量在时刻dx内逃逸到空气中去;由此得出,固体的这个无穷小部分实际保留由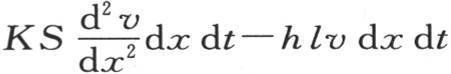 所表示的热量,这个量使它的温度发生变化。我们应当考察这个变化的总量。
所表示的热量,这个量使它的温度发生变化。我们应当考察这个变化的总量。
105 系数C表示把所说的单位重量的这种物质从0度提高到1度需要多少热;所以,用密度D乘这个无穷小薄片的体积Sdx,得到它的重量,再乘以比热C,我们就得到作为使这个薄片的体积从0度升高到1度的热量CDSdx。因此,引起增加等于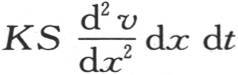
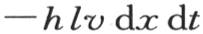 的热量的温度增量,由最后这个量除以CDSdx而得到。因此,按惯例,用
的热量的温度增量,由最后这个量除以CDSdx而得到。因此,按惯例,用
表示在时刻dt内所发生的温度的增量,我们有方程

我们将在后面阐明为确定通解而可能对这个方程所作的运用,并且阐明这个问题的困难之所在;此处我们只给出与这个臂环的永恒温度有关的一个注记。
106 假定由于环平面是水平的,因而发挥一个恒定作用的每一个热源被放在不同点m,n,p,q,等等的下面;热将在这个固体中传导,并且由于通过表面而被消耗的热不断由热源所发出的热来补偿,所以,这个固体的每一截面温度将愈来愈趋近于一个随不同截面而异的定值。为了用方程(a)表示若一旦产生,它们就自行存在的这后一种温度的规律,我们应当假定量v不随t而变化;这就消去了项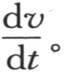
因此我们有方程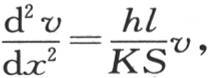 所以
所以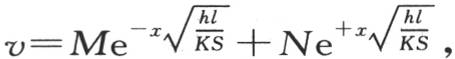 M和N是两个常数 【1】 。
M和N是两个常数 【1】 。
107 假定位于两个相邻热源之间的部分环周长被分成若干等份,分界点与原点的距离为x1 ,x2 ,x3 ,x4 ,…,用v1 ,v2 ,v3 ,v4 ,…表示分界点的温度;当两个常数由对应于热源的两个值确定之后,v和x之间的关系就由前述方程给出。用α表示量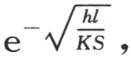 用λ表示两个相邻的分界点的距离x2 -x1 ,我们有方程:v1 =Mαx1 +Nα-x1 ,v2 =Mαλ ·αx1 +Nα-λ α-x1 ,v3 =Mα2λ αx1 +Mα-2λ α-x1 ,因此我们得出下述关系
用λ表示两个相邻的分界点的距离x2 -x1 ,我们有方程:v1 =Mαx1 +Nα-x1 ,v2 =Mαλ ·αx1 +Nα-λ α-x1 ,v3 =Mα2λ αx1 +Mα-2λ α-x1 ,因此我们得出下述关系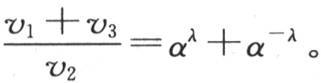
对于温度为v2 ,v3 ,v4 的三个点,一般地,对于任何相邻的三个点,我们都会得到一个类似的结果。由此得到,如果我们观察均处在同样两个热源m和n之间、且由一个恒定间隔λ分开的几个相邻点的温度v1 ,v2 ,v3 ,v4 ,v5 ,…,那么我们会看到,任何三个相邻的温度都是这样的:两端之和除以中点的温度得一个常数商αλ +α-λ 。
108 如果在包含在任何别的两个热源n和p之间的空间中我们观察由同一间隔λ分开的别的不同点的温度,那么我们同样会得到,对于任何三个相邻的点,两端温度之和除以中点的温度得同一常数商αλ +α-λ 。这个商值既与热源位置无关,也与热源强度无关。
109 设q是这个常数值,我们有方程v3 =qv2 -v;由此我们看到,当周长被分成几等份时,包含在两个相邻热源之间的分界点的温度,由一个循环级数的那些项来表示,这个级数的相关比(scale of relation)由q和-1两项组成。
实验已经充分确证了这个结果。我们曾让一个金属环受不同热源的恒定且同时的作用,我们观察由若干恒定间隔分开的几点的恒定温度;我们总发现,不脱离一个热源的任何三个相邻点的温度,都有所说的这个关系。即使热源增加,且无论怎样安排它们,商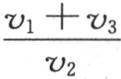 的数值都不会发生任何变化;它仅仅取决于环的尺寸和质,而与这个固体的受热方式无关。
的数值都不会发生任何变化;它仅仅取决于环的尺寸和质,而与这个固体的受热方式无关。
110 当我们由观察得到常数商q或者是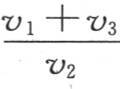 时,通过方程αλ +α-λ =q,就可以从中导出αλ 的值。这个方程的一个根是αλ ,另一个是α-λ 。由于这个量被确定,我们就可以由它导出比
时,通过方程αλ +α-λ =q,就可以从中导出αλ 的值。这个方程的一个根是αλ ,另一个是α-λ 。由于这个量被确定,我们就可以由它导出比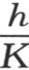 的值,这个值是
的值,这个值是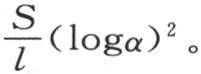 用ω表示αλ ,我们有ω2 -qω+1=0。因此,用方程ω2 -qω+1=0的一个根的双曲对数的平方乘
用ω表示αλ ,我们有ω2 -qω+1=0。因此,用方程ω2 -qω+1=0的一个根的双曲对数的平方乘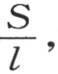 并且用λ2 除这个积,我们就得到两个热导率的比。
并且用λ2 除这个积,我们就得到两个热导率的比。
第二节 实心球中变化的热运动方程
111 形如球体的一个同质固体物质,在保持永恒温度1的一种介质中浸泡无穷时间,然后让它受保持0度并且以一定速移动的空气的作用;需要确定这个物体在整个冷却时间内的连续状态。
用x表示任一点与球心的距离,用v表示在历经时间t之后这同一点的温度;为使这个问题更一般化,假定处在与球心距离为x的所有点的共同初始温度随不同的x值而异;若浸泡尚未持续无穷时间,则就是这种情况。
这个固体与球心等距的那些点有相同的温度,因此,v是x和t的某个函数。当我们假定t=0时,这个函数的值就应当与完全任意给定的初始状态一致。
112 我们要考虑由半径为x和x+dx的两个球面所围成的无穷薄壳层中的瞬时热运动:在一个无穷小时刻dt内,过半径为x的较小的面,并从这个固体最靠近球心的部分进入这个球形壳层的热量,等于四个因子的积,这四个因子是热导率K,时间dt,壳面面积4πx2 ,以及比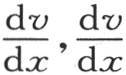 取负号;这个积由
取负号;这个积由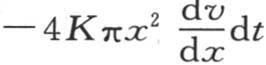 来表示。
来表示。
为了确定在这同一时刻内流过这同一壳层的第二个面、并从这个壳层进入包围它的这个固体的这一部分的热量,就应当在前一个表达式中,把x变成x+dx:即应当把项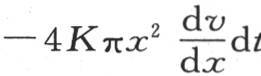 对x的微分加到这一项上去。因此我们得到作为经过第二个面而离开这个球形壳层的热量表达式
对x的微分加到这一项上去。因此我们得到作为经过第二个面而离开这个球形壳层的热量表达式 ;如果我们从进入第一个面的量中减去这个量,我们就有
;如果我们从进入第一个面的量中减去这个量,我们就有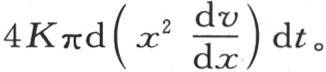 显然,这个差就是积聚在这个中间壳层中的热量,这个热量的作用会改变它的温度。
显然,这个差就是积聚在这个中间壳层中的热量,这个热量的作用会改变它的温度。
113 系数C表示使一个确定重量的单位从0度升至1度所需要的热量;D是单位重量的体积,4πx2 dx2 是中间薄层的体积,它与它只相差一个可以忽略不计的量:所以,4πCDx2 dx是使中间壳层从0度升至1度所需要的热量。因此,必须用4πCDx2 dx除这个壳层中所积聚的热量,这样,我们得到它的温度v在时间dt内的增量。因此,我们得到方程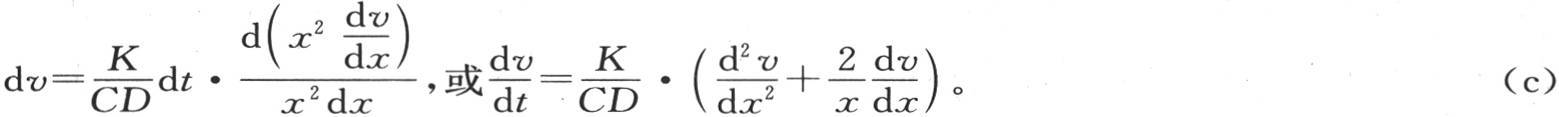
114 上述方程表示这个固体内部的热运动规律,不过表面上的点的温度还受到我们应当表示的一个特殊条件的支配。与表面状态有关的这个条件可随所讨论的问题的性质而变化:例如我们可以假定在加热这个球体并使它的分子升至沸水温度后,再对表面上所有的点给定0度温度,并且以任一外因使它们保持这个0度温度,从而使冷却发生作用。在这种情况下,我们可以设想一个球,这个球的变化状态是需要确定的,这个球由一个极薄的壳层所覆盖,冷却因素就是在这个壳层上发挥它的作用的,我们可以假定,1°,这个无穷薄的壳层附着在这个固体上,其物质与这个固体的物质相同,并且像这个物体其他部分一样成为这个物体的一部分,2°,这个壳层的所有分子都处于0度,它由始终防止这一温度高于或低于0度的一个原因所维持。为了从理论上表述这个条件,当我们对x给定等于球半径的全值X时,无论t取什么值,我们都应当让包含x和t的这个函数v变成0。在这个假定下,如果我们用φ(x,t)表示x和t的这个函数,它表示v的值,那么我们就有两个方程: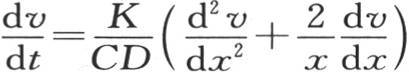 和φ(X,t)=0。此外,初始状态应当由这同一个方程φ(x,t)来表示:因此我们有作为第二个条件的φ(x,0)=1。这样,在我们开始已经描述过的这个假定下,一个固体球的变化状态就由应当满足上面三个方程的一个函数v来表示。第一个条件是一般的,它在每一时刻都属于这个物体的所有点;第二个只对表面分子起作用,第三个则仅仅属于初始温度。
和φ(X,t)=0。此外,初始状态应当由这同一个方程φ(x,t)来表示:因此我们有作为第二个条件的φ(x,0)=1。这样,在我们开始已经描述过的这个假定下,一个固体球的变化状态就由应当满足上面三个方程的一个函数v来表示。第一个条件是一般的,它在每一时刻都属于这个物体的所有点;第二个只对表面分子起作用,第三个则仅仅属于初始温度。
115 如果这个固体在空气中冷却,则第二个方程就不一样了;这时,我们应当设想这个极薄壳层由某一外因保持在如像下述情况的一种状态中:每一时刻从球体逃逸掉等于有介质时介质会从中带走的热量。
现在,在一个无穷小时刻dt内,在这个固体内部流过位于距离为x的球面的热量,等于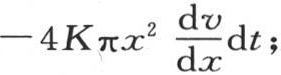 这个一般表达式适用于所有x的值。因此,假定x=X,我们就可以确定在这个球的变化状态中流过形成它的边界的极薄壳层的热量;另一方面,这个固体的外表面有一变化的温度,我们用v来表示这一温度,这个外表面,允许一定的热量逃逸到空气中去,这个热量与温度,与表面面积4πX2 成正比。这个量的值是4hπX2 Vdt。
这个一般表达式适用于所有x的值。因此,假定x=X,我们就可以确定在这个球的变化状态中流过形成它的边界的极薄壳层的热量;另一方面,这个固体的外表面有一变化的温度,我们用v来表示这一温度,这个外表面,允许一定的热量逃逸到空气中去,这个热量与温度,与表面面积4πX2 成正比。这个量的值是4hπX2 Vdt。
如假设,为了表示这个壳层的作用在每一时刻内代替介质的存在所产生的作用,只需要使量4hπX2 Vdt等于表达式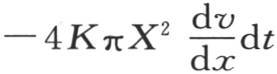 在我们对x给定其全值X时所得到的值就够了。因此我们得到方程
在我们对x给定其全值X时所得到的值就够了。因此我们得到方程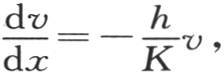 当我们在
当我们在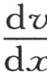 和v这两个函数中用x的值X代替x时,这个方程肯定成立,我们用
和v这两个函数中用x的值X代替x时,这个方程肯定成立,我们用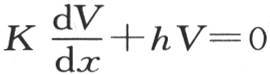 的形式表示它。
的形式表示它。
116 因此,在x=X时,所取的这个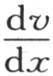 的值,与对应于同一点的v值,肯定有一个常数比
的值,与对应于同一点的v值,肯定有一个常数比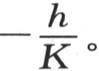 这样,我们假定这个冷却的外因始终以下述方式决定这个极薄壳层的状态;对应于x=X,由这个状态所产生的
这样,我们假定这个冷却的外因始终以下述方式决定这个极薄壳层的状态;对应于x=X,由这个状态所产生的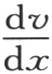 的值与v的值成正比,这两个量的常数比是
的值与v的值成正比,这两个量的常数比是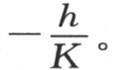 由于这个条件因始终存在使
由于这个条件因始终存在使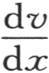 的极值不是别的而只能是
的极值不是别的而只能是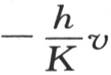 的某种原因而被满足,所以,这个壳层的作用将代替空气的作用。
的某种原因而被满足,所以,这个壳层的作用将代替空气的作用。
不必假定这个壳层是极薄的,在后面我们将看到,它可以有一个不定的厚度。此处把厚度看做无穷小,是为了把注意力集中在这个固体的表面状态上。
117 因此,用以确定函数φ(x,t)或者是v的三个方程如下: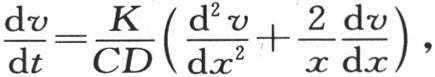
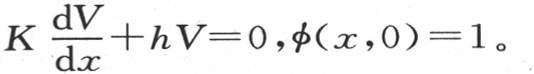
第一个适用于x和t的所有可能的值;无论t取何值,当x=X时,第二个方程成立;无论x取何值,当t=0时,第三个方程成立。
应当假定,在初始状态中,所有球形薄层均无相同的温度:倘若设想浸泡尚未持续无穷长的时间,则必然会出现这种情况。在比前述情况更一般的这种情况下,这个被给定的函数,表示处在与球心的距离为x的分子的初始温度,用F(x)来表示;这样,第三个方程就由φ(x,0)这样一个方程代替。
剩下的只是一个纯分析问题,它的解将在下面几章的一章中给出。它主要是借助于这个一般条件和它所服从的两个具体条件来求v的值。
第三节 实圆柱中变化的热运动方程
118 一个无穷长的实圆柱,它的边与它的圆形基底垂直,由于完全浸没在温度处处相同的某种液体中,而逐渐被加热,加热的方式是这样的:与轴等距的所有点都得到相同的温度;随后让它受一种较冷的气流的作用;需要确定的是在一个给定的时间之后不同薄层的温度。
x表示某个圆柱面的半径,这个圆柱面上的所有点与轴等距;X是这个圆柱体的半径;自冷却开始时,在历经由t所表示的某个时间之后,这个圆柱体的那些处在与轴相距x的点的温度,是v。因此,v是x和t的函数,如果在这个函数中使t等于0,则由此得到的这个x的函数必然满足初始状态,初始状态是任意的。
119 考虑在一个半径为x的面和另一个半径为x+dx的面之间的这个圆柱的一个无穷薄的部分中的热运动。在时刻dt内,这一部分从它所围住的这个固体的那一部分中所得到的热量,即在同一时间内,经过其半径为x、其长度 【2】 假定与单位相等的这个圆柱面的热量,由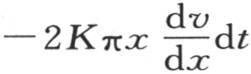 来表示。
来表示。
为了求过半径为x+dx的第二个面而从这个无穷薄的壳层进入围住它的这个固体的那部分的热量,我们应当在前一个表达式中,把x变成x+dx,或者是同样地,把项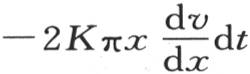 对x的微分加到该项上去。这样,所得到的热和所失去的热的差,或者是说聚集在这个无穷薄的壳层中决定着温度变化的热量,是取反号的这同一个微分,或者是
对x的微分加到该项上去。这样,所得到的热和所失去的热的差,或者是说聚集在这个无穷薄的壳层中决定着温度变化的热量,是取反号的这同一个微分,或者是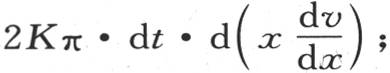
另一方面,这个中间壳层的体积是2πxdx,并且2CDπxdx表示把它从0度升至1度所需要的热量,C是比热,D是密度。因此,商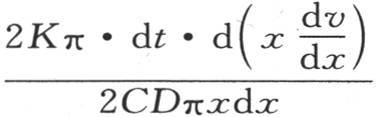 是这一温度在时刻dt内所得到的增量。因此我们得到方程
是这一温度在时刻dt内所得到的增量。因此我们得到方程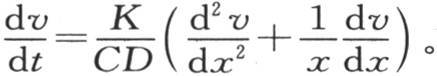
120 由于在时刻dt内,经过半径为x的圆柱面的热量,一般地,由 来表示,所以,在前一值中使x=X,则我们就得到在同一时间内从这个固体表面所逃逸的热量;另一方面,弥散到空气中去的这个相同的量,根据热传导原理,等于2πXhvdt;因此,在这个面上,我们肯定有定义方程
来表示,所以,在前一值中使x=X,则我们就得到在同一时间内从这个固体表面所逃逸的热量;另一方面,弥散到空气中去的这个相同的量,根据热传导原理,等于2πXhvdt;因此,在这个面上,我们肯定有定义方程 我们在关于球的那些目中,或者是在对任一形状的物体给出一般方程的那些目中,以更大的篇幅解释了这些方程的性质,因此,表示无穷圆柱中的热运动的函数v应当满足,
我们在关于球的那些目中,或者是在对任一形状的物体给出一般方程的那些目中,以更大的篇幅解释了这些方程的性质,因此,表示无穷圆柱中的热运动的函数v应当满足,
第一,一般方程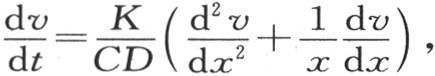 无论x和t如何,它都适用;
无论x和t如何,它都适用;
第二,定义方程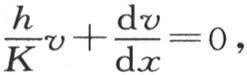 当x=X时,无论变量t如何,它都成立;
当x=X时,无论变量t如何,它都成立;
第三,定义方程v=F(x)。当使t=0时,无论变量x如何,v的所有值都应当满足最后这个条件。任意函数F(x)被看做是已知的;它对应于初始状态。
第四节 无穷长实棱柱中的均匀热运动方程
121 一个棱柱棒的一端浸在使该端保持温度A的一个恒定热源中;这根棒的长度无穷的其余部分不断受到保持0度的均匀气流的作用;需要确定的是这根棒的一个已知点所能达到的最高温度。
这个问题与第73目的问题不同,因为,为了得到一个精确的解,我们现在必须计及这个固体的所有方面。
的确,我们曾经假定,在一根很细的棒中,同一个截面的所有点都得到明显相等的温度;然而,某种不可靠性可能会隐含在这一假定的结果中。因此,最好是严格地解决这个问题,然后用分析来考查到什么时候,在什么条件下,我们才可以认为同一截面上的不同点的温度是相等的。
122 与这根棒的长成直角的截面是边为2l的一个正方形,这根棒的轴是x轴,原点在端面A上。这根棒上的一点的三个直角坐标是x,y,z,v表示同一点的固定温度。
问题在于要确定,只要与热源相连通的端面A的所有点都一直受到永恒温度A的作用,为使这根棒上的不同点的温度能够继续存在而无任何变化,我们应当对这些不同的点赋予怎样的一些温度;因此,v是x,y和z的一个函数。
123 考虑围在与x,y和z的这三个轴垂直的六个平面之间的一个棱柱分子中的热运动。前三个面经过坐标为x,y,z的点m,另外三个经过坐标为x+dx,y+dy,z+dz的点m′。
为了求在单位时间内通过点m并且与x轴垂直地经过第一个面而进入这个分子的热量,我们应当记住,在这个面上的这个分子的表面积是dy dz,流过这个面积的热量,根据第98目的定理,等于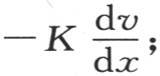 因此,这个分子所得到的通过矩形dy dz并且经过点m的一个热量由
因此,这个分子所得到的通过矩形dy dz并且经过点m的一个热量由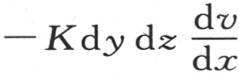 来表示。为了求过其对面而从这个分子所逃逸的热量,我们应当在前一个式子中,用x+dx代替x,或者同样地,在这个式子中再加上它只对x的微分;由此我们得到,这个分子在它与x轴垂直的第二个面上所失掉的热量等于
来表示。为了求过其对面而从这个分子所逃逸的热量,我们应当在前一个式子中,用x+dx代替x,或者同样地,在这个式子中再加上它只对x的微分;由此我们得到,这个分子在它与x轴垂直的第二个面上所失掉的热量等于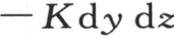
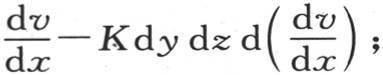 因此,我们应当从在对面所进入的热量中减去这个量;这两个量的差是
因此,我们应当从在对面所进入的热量中减去这个量;这两个量的差是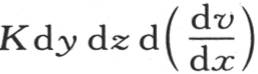 或
或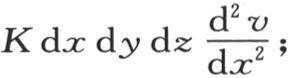 由于是沿x轴的方向传导,所以这个式子表示在这个分子中所聚积的热量;如果它不能与在别的方向上所失去的热量平衡,那么所聚积的热就会使这个分子的温度发生变化。
由于是沿x轴的方向传导,所以这个式子表示在这个分子中所聚积的热量;如果它不能与在别的方向上所失去的热量平衡,那么所聚积的热就会使这个分子的温度发生变化。
用同样的方法得到,等于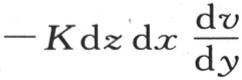 的热量经过垂直于y轴的这个平面上的点m而进入这个分子,从对面所逃逸的热量是
的热量经过垂直于y轴的这个平面上的点m而进入这个分子,从对面所逃逸的热量是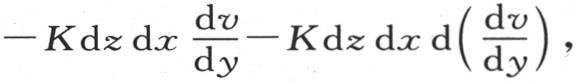 最后的微分只对y取。这样,这两个量的差,或
最后的微分只对y取。这样,这两个量的差,或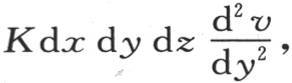 由于是沿y轴的方向传导,就表示这个分子所得到的热量。
由于是沿y轴的方向传导,就表示这个分子所得到的热量。
最后,我们用同样的方法证明,由于是沿z轴的方向传导,这个分子得到等于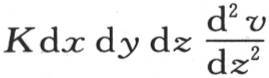 的热量。现在,为使温度不至于发生任何变化,这个分子就应当保持和它开始时所保持的一样多的热,因此,它在某一个方向所得到的热就应当与它在另一个方向所失去的热平衡。这样,所得到的这三个热量的和就应当等于0;因此,我们建立方程
的热量。现在,为使温度不至于发生任何变化,这个分子就应当保持和它开始时所保持的一样多的热,因此,它在某一个方向所得到的热就应当与它在另一个方向所失去的热平衡。这样,所得到的这三个热量的和就应当等于0;因此,我们建立方程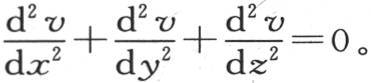
124 现在剩下的是表示与这个表面有关的一些条件。如果我们假定点m属于这个棱柱棒的某个面,这个面与z轴垂直,那么我们会看到,在单位时间内,矩形dx dy允许等于Vh dx dy的热量逃逸到空气中去,V表示这个表面上的点m的温度,即表示在使得z等于这个棱柱的直径的一半l时所要求的这个函数φ(x,y,z)所达到的值。另一方面,由于这些棱柱分子的作用,在单位时间内,经过位于这个棱柱内且与z轴垂直的无穷小的面ω的热量,根据上面提供的定理,等于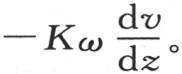 这个表达式是一般的,并且,当把它应用于坐标z得到其全值l的那些点时,我们由此得到,在函数
这个表达式是一般的,并且,当把它应用于坐标z得到其全值l的那些点时,我们由此得到,在函数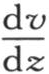 中,对z给定其全值l,则经过这个面上的矩形dx dy的热量,是
中,对z给定其全值l,则经过这个面上的矩形dx dy的热量,是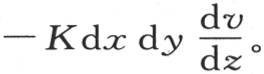 因此,为使这些分子的作用能与介质的作用一致,这两个量
因此,为使这些分子的作用能与介质的作用一致,这两个量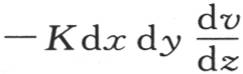 和h dx dy v就应当相等。当我们在函数
和h dx dy v就应当相等。当我们在函数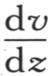 和v中,对z给定它在所考虑过的第一个面的对面所具有的值-l时,这个等式也应当成立。此外,由于经过垂直于y轴的一个无穷小的面ω的热量是
和v中,对z给定它在所考虑过的第一个面的对面所具有的值-l时,这个等式也应当成立。此外,由于经过垂直于y轴的一个无穷小的面ω的热量是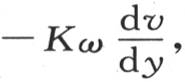 因此,在函数
因此,在函数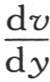 中对y给定其全值l时,则经过与y轴垂直的这个棱柱的某一个面上的矩形dz dx的热量,是
中对y给定其全值l时,则经过与y轴垂直的这个棱柱的某一个面上的矩形dz dx的热量,是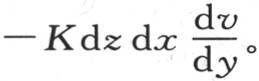 现在,这个矩形dz dx允许由h vdx dy所表示的热量逃逸到空气中去;因此,当在函数v和
现在,这个矩形dz dx允许由h vdx dy所表示的热量逃逸到空气中去;因此,当在函数v和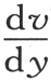 中使y等于l或者-l时,方程
中使y等于l或者-l时,方程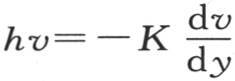 必然成立。
必然成立。
125 由假设,当我们假定x=0时,无论y和z的值如何,函数v的值都必然等于A。因此,所求的函数v由下述条件确定:
第一,对x,y,z的所有值,它满足一般方程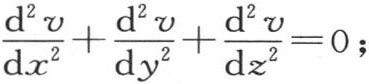
第二,当y等于l或者-l时,无论x和z如何,它满足方程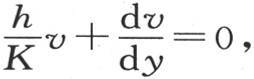 或者,当z等于l或者-l时,无论x和y如何,它满足方程
或者,当z等于l或者-l时,无论x和y如何,它满足方程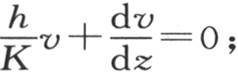
第三,当x=0时,无论y和z如何,它满足方程v=A。
第五节 实立方体中变化的热运动方程
126 把一个所有点都达到相同温度的实立方体放在保持0度的均匀气流中。需要确定的是这个物体在整个冷却期间的连续状态。
取这个立方体的中心为直角坐标系的原点;从这一点到各面的垂线为x,y,z轴;立方体的边为2l,v是坐标为x,y,z的一点自冷却开始到历经时间t之后所降至的温度。问题在于确定依x,y,z而定的函数v。
127 为了建立v所应当满足的一般方程,我们应当确定这个固体的一个无穷小部分,在时刻dt内,由于与它挨得极近的那些分子的作用,所应当经历的温度变化。这样,我们考虑围在六直角平面内的一个棱柱分子;六直角平面的前三个面经过坐标为x,y,z的点m,另外三个面经过坐标为x+dx,y+dy,z+dz的点m′。
在时刻dt内,过垂直于x的第一个矩形dy dz而进入这个分子的热量,是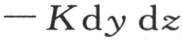
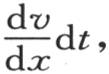 并且在同一时间内,过对面而从这个分子中所逃逸的热量,由在前一表达式中用x+dx代替x而得到,它是
并且在同一时间内,过对面而从这个分子中所逃逸的热量,由在前一表达式中用x+dx代替x而得到,它是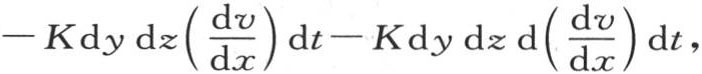 这个微分只对x取。在时刻dt内,过垂直于y轴的第一个矩形dz dx而进入这个分子的热量,是
这个微分只对x取。在时刻dt内,过垂直于y轴的第一个矩形dz dx而进入这个分子的热量,是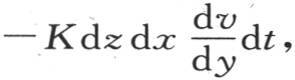 在同一时间内,过对面而从这个分子中所逃逸的热量,是
在同一时间内,过对面而从这个分子中所逃逸的热量,是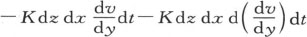 这个微分只对y取。在时刻dt内,这个分子过它垂直于z轴的下平面所得到的热量,是
这个微分只对y取。在时刻dt内,这个分子过它垂直于z轴的下平面所得到的热量,是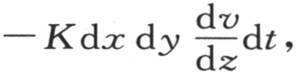 而过其对面所失去的热量,是
而过其对面所失去的热量,是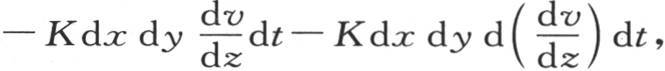 这个微分只对z取。
这个微分只对z取。
现在,我们应当从这个分子所得到的热量的和中,减去从它那里所逃逸的全部热量的和,差是确定它在这个时刻内的温度增量的量:这个差是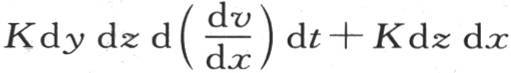
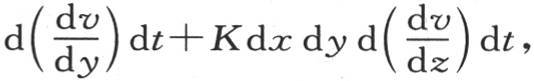 或者是
或者是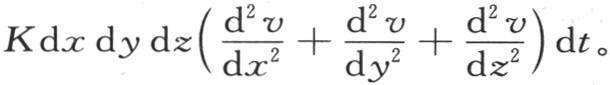
128 如果用使这个分子从0度升至1度所需的量除刚才得到的这个量,那么在时刻dt内所产生的温度增量就成为已知的。现在这前一个量是CD dx dy dz:C表示这一物质的热容量;D表示其密度,dx dy dz表示这个分子的体积。因此,这个固体内部的热运动由方程
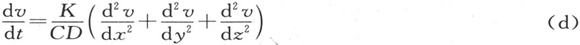
来表示。
129 剩下的问题是建立关于表面状态的方程,根据我们已经建立的原理,这不会有任何困难。事实上,在时刻dt内,过处在与x轴垂直的一个平面上的矩形dz dy的热量,是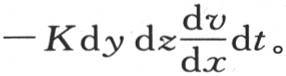 当x的值等于这个棱柱厚度的一半l时,这个结果应当成立,它适用于这个固体的所有点。在这种情况下,由于矩形dy dz在表面上,所以,在时刻dt内,过它并弥散到空气中去的热量,由hv dy dz dt来表示,因此当x=l时,我们应当有方程
当x的值等于这个棱柱厚度的一半l时,这个结果应当成立,它适用于这个固体的所有点。在这种情况下,由于矩形dy dz在表面上,所以,在时刻dt内,过它并弥散到空气中去的热量,由hv dy dz dt来表示,因此当x=l时,我们应当有方程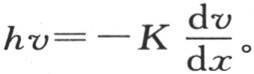 当x=-l时这一条件亦被满足。
当x=-l时这一条件亦被满足。
我们还可以得到,由于过处于与y轴垂直的一个平面上的矩形dy dx的热量,一般地,是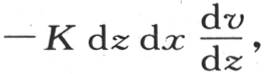 并且过这同一矩形而从表面逃逸到空气中去的热量是hv dz dx dt,所以,当y=l或者是-l时,我们肯定有方程
并且过这同一矩形而从表面逃逸到空气中去的热量是hv dz dx dt,所以,当y=l或者是-l时,我们肯定有方程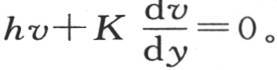 最后,我们以同样的方法得到定义方程
最后,我们以同样的方法得到定义方程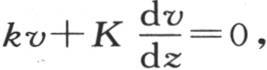 它在z=l或者是-l时成立。
它在z=l或者是-l时成立。
130 因此,表示在实立方体的固体内变化的热运动的这个所求方程,应当以下述条件来确定:
第一,它满足一般方程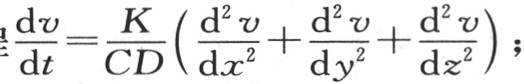
第二,它满足三个定义方程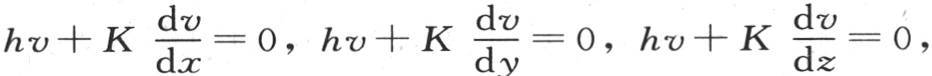 它们在x=±l,y=±l,z=±l时成立;
它们在x=±l,y=±l,z=±l时成立;
第三,如果在包含x,y,z,t的函数v中,无论x,y和z的值如何,我们都取t=0,那么,由假定,我们应当有v=A,它是温度的初始值和公共值。
131 在前述问题中所得到的这个方程表示所有固体内部的热运动。事实上,无论物体形状如何,显然,通过把它们分解成棱柱状的分子,我们就可以得到这个结果。因此,我们可以只限于以这种方式来论证热传导方程。然而,为了使原理的展示更全面,为了使我们能把用来建立固体内部的热传导的一般方程和关于表面状态的方程的定理在少数几个相邻的目中集中起来,我们将在下面两节中开始研究这些方程而不涉及任何特殊的问题,也不回到我们在导言中解释过的基本命题上来。
第六节 固体内热传导的一般方程
132 定理1. 如果围在六直角平面之间的一个同质固体的不同点有由线性方程

所确定的有效温度,如果处在界定这个棱柱的六个平面的外表面上的分子以任一原因保持由方程(a)所表示的温度:那么,处在这个物体内部的所有分子将自行保持它们的有效温度,因此这个棱柱的状态不发生任何变化。
v表示坐标为x,y,z的点的有效温度,A,a,b,c是常系数。
为了证明这个命题,考虑这个固体中处在同一直线mμ上的任意三点m,M,μ,点M把这条直线分成两等份;用x,y,z表示点M的坐标,用v表示其温度,用x+α,y+β,z+γ表示点μ的坐标,用w表示其温度,x-α,y-β,z-γ表示点m的坐标,u表示它的温度,我们有v=A-ax-by-cz,w=A-a(x+α)-b(y+β)-c(z+γ),u=A-a(x-α)-b(y-β)-c(z-γ),所以我们得到,v-w=aα+bβ+cγ,和u-v=aα+bβ+cγ;因此v-w=u-v。
现在,一点从另一点所得到的热量取决于这两点间的距离和它们的温差。这样,点M对μ的作用等于m对M的作用;因此,点M从m处得到与它向点μ所放出的一样多的热。
无论经过点M并且被分成两等份的这条直线的方向和长度如何,我们都得到同样的结果。因此,对于这一点来说,不可能改变它的温度,因为它从所有部分得到的热同它放出的热一样多。
同样的推理适用于所有别的点;因此,这个固体的状态不会发生任何变化。
133 推论1. 一个固体被包围在两个无穷平行平面A和B之间,如果假定它的不同点的有效温度由方程v=1-z来表示,围住它的两个平面以任一原因保持A为1、B为0的温度;那么,倘若我们使A=1,a=0,b=0,c=1,则这个特例包含在上述定理中。
134 推论2. 如果在这同一固体内,我们设想平行于界定它的那些面的一个平面M,那么我们会看到,一定的热量在单位时间内流过这个平面;因为,挨得很近的两点,如m和n,其中一个在这个平面下方,另一个在它上方,受热不等;因此,温度高的第一点在每一时刻内肯定向第二点发出一定的热量,根据这个物体的质和这两个分子的距离,在某些情况下,这个热量可能很小,甚至难以察觉。
对于由这个平面分开的任何两点,它同样成立。受热多的分子向别的分子发出一定的热量,这些部分作用的和,或者说过这个平面所发出的所有热量,构成一个其值不变的连续热流量,因为所有分子都保持其自己的温度。容易证明,这个热流量,或者说在单位时间内,过平面M的热量,等于在同一时间内过平行于第一个平面的另一个平面N的热流量。事实上,围在两个平面M和N之间的这个物体的部分不断过面M得到和它过面N所失去的一样多的热。如果过面M而进入所考虑的物质的这个部分的热量不等于过对面N所逃逸的热量,那么,围在这两个平面之间的这个固体就会得到新的热,或者会失去它所有的一部分热,它的温度就不是不变的,这与前述定理矛盾。
135 一个给定的物体的热导率的量度,被看做是在组成这个物体、并且围在两个平行平面之间的一个无穷固体中,在单位时间内,流过平行于外平面的任一中间平面上的单位面积的热量,这两个外平面之间的距离等于单位长度,其中一个保持1度,另一个保持0度。过这个棱柱全面积的这个恒定热流量,由系数K表示,它是热导率的量度。
136 引理. 如果我们假定上一目所讨论的这个固体的所有温度都乘以任一数g,因此温度方程是v=g-gz,而不是v=1-z,如果两个外平面一个保持g度,另一个保持0度,那么,在这第二种假定下,这一恒定热流量,或在单位时间内,过平行于这两个基底的中间平面上的单位面积的热量,就等于前一热流量与g的积。
事实上,由于所有温度都以1与g的比增加,所以,任两点m和μ的温差都以同一个比增加。因此,根据热传导原理,为了确定m在第二种假定下向μ所发出的热量,我们应当用g乘同一点m在第一种假定下向μ所发出的热量。对于任何别的两点,这同样成立。现在,过一个平面M的热量,等于处在这个平面同一边的点 作用于处在另一边的点
作用于处在另一边的点 的所有作用的和。因此,如果在第一种假定下的这个恒定热流量用K表示,那么,当我们用g乘所有这些温度时,它等于gK。
的所有作用的和。因此,如果在第一种假定下的这个恒定热流量用K表示,那么,当我们用g乘所有这些温度时,它等于gK。
137 定理2. 如果有一个棱柱,它的不变温度由方程v=A-ax-by-cz来表示,并且它由六直角平面所固定,它的所有点都保持由前一个方程所确定的不变温度,在这样一个棱柱中,在单位时间内,经过在垂直于z轴的任一中间平面上的单位面积的热量,与包围在两个无穷平行平面之间,其不变温度的方程是v=c-cy的一个同质固体中的不变热流量相同。
为证此,让我们考虑在这个棱柱中,和在这个无穷固体中,由垂直于z轴的平面M所分开的两个极近的点m和μ;μ在这个平面的上方,m在它的下方(见图4),在这同一平面的下方,让我们取一点m′,使得从点μ到这个平面的垂线也垂直于距离mm′,并交于这个距离的中点h。用x,y,z+h表示点μ的坐标,它的温度是w,用x-α,y-β,z表示点m的坐标,其温度为v,用x+α,y+β,z表示m′的坐标,它的温度为v′。
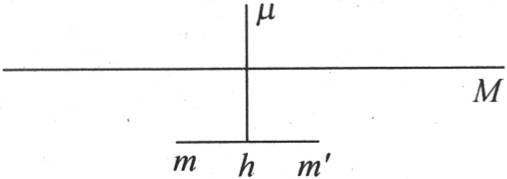
图4
m对μ的作用,或者说m在一定时间内向μ所发出的热量,可以用q(v-w)来表示。因子q取决于距离mμ和这个物体的质。因此,m′对μ的作用由q(v′-w)表示;因子q与前一个表达式中的相同;这样,m对μ和m′对μ的这两个作用的和,或μ从m和m′那里所得到的热量,由q(v-w+v′-w)来表示。现在,如果点m,μ,m′属于这个棱柱,那么我们有w=A-ax-by-c(z+h),v=A-a(x-α)-b(y-β)-cz,和v′=A-a(x+α)-b(y+β)-cz;如果同样这几点属于一个无穷固体,那么由假定,我们有w=c-c(z+h),v=c-cz,和v′=c-cz。在第一种情况中,我们得到q(v-w+v′-w)≡2qch,在第二种情况中,我们仍然有相同的结果。因此,当恒温方程是v=A-ax-by-cz时,在第一种假定下,μ从m和m′那里所得到的热量,与当恒温方程是v=c-cz时,μ从m和m′那里所得到的热量相等。
对于任意的其他三点m′,μ,m″,只要第二点μ′处在与其他两点相等的距离上,并且这个等腰三角形m′,μ′,m″的高与z轴平行,则可以得出同样的结论。现在,过任一平面M的热量,等于位于这个平面一边的所有点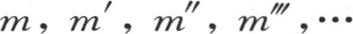 对位于另一边的所有点
对位于另一边的所有点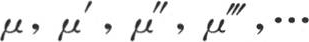 所施加的作用的和:因此,在单位时间内,过这个无穷固体中的平面M的一个确定部分的恒定热流量,等于在这同一时间内,流过这个棱柱中的平面M的相同部分的热量,这个棱柱的所有温度都由方程v=A-ax-by-cz来表示。
所施加的作用的和:因此,在单位时间内,过这个无穷固体中的平面M的一个确定部分的恒定热流量,等于在这同一时间内,流过这个棱柱中的平面M的相同部分的热量,这个棱柱的所有温度都由方程v=A-ax-by-cz来表示。
138 推论. 当这个热流量所经过的这个平面的部分是单位面积时,它在这个无穷固体中取值cK,它在这个棱柱中也取相同的值cK或者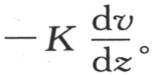 用同样的方法可以证明:在单位时间内,在这同一棱柱中过垂直于y轴的任一平面上的单位面积所产生的恒定热流量,等于bK或者
用同样的方法可以证明:在单位时间内,在这同一棱柱中过垂直于y轴的任一平面上的单位面积所产生的恒定热流量,等于bK或者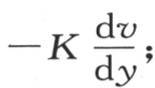 过垂直于x轴的一个平面的这种热流量取值aK或者
过垂直于x轴的一个平面的这种热流量取值aK或者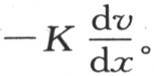
139 我们在前几目中所证明的这些命题也适用于分子的瞬时作用在物体内部可以影响到一段明显的距离时的情况。在这种情况中,我们应当假定,使这个物体外层保持由这个线性方程所表示的状态的原因,影响这个物体到一个有限深度。所有的观察都证明,在固体或者是在液体中,所讨论的这个距离都非常小。
140 定理3. 如果一个固体的点的温度由方程v=f(x,y,z)表示,其中x,y,z是在历经时间t后温度等于v的一个分子的坐标;那么,过引自这个固体中垂直于某一个轴的一个平面的一部分的热流量,就不再是恒定的了;它的值随这个平面的不同部分而异,也随时间而异。这个变量可由分析来确定。
设ω是圆心与这个固体的点m重合、面与纵坐标z垂直的一个无穷小的圆;在时刻dt内,有一定的热量流过这个圆,它们从这个圆平面下面的圆的部分而进入上面的部分。这个热流由离开下面一点过这个小平面ω的一点而到达上面一点的所有热辐射线组成。我们要证明,这个热流量的值的表达式是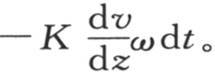
让我们用x′,y′,z′表示温度为v′的点m的坐标;假定所有别的分子都以这一点m作为平行于前坐标轴的新的轴原点:设ξ,η,ζ是相对于原点m的一点的三个坐标;为表示与点m挨得无穷近的一个分子的有效温度w,我们有线性方程
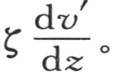 系数v′,
系数v′,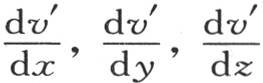 是在函数v,
是在函数v,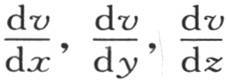 中用常量x′,y′,z′代替变量x,y,z所得到的值,x′,y′,z′是点m到前三个坐标x,y,z的距离。
中用常量x′,y′,z′代替变量x,y,z所得到的值,x′,y′,z′是点m到前三个坐标x,y,z的距离。
现在假定点m也是围在六直角平面中的一个矩形棱柱的内分子,这六直角平面与原点为m的三条轴垂直;体积有限的这个棱柱的每一个分子的有效温度w,由线性方程w=A+aξ+bη+cζ来表示,界定这个棱柱的这六个面保持最后这个方程所赋予它们的固定温度。这些内分子的状态也是永恒的,并且,由表达式-Kcwdt所测定的一个热量在时刻dt内流过这个圆ω。
如此,如果我们把量v′,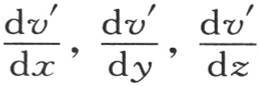 作为常数A,a,b,c的值,那么这个棱柱的固定状态就由方程
作为常数A,a,b,c的值,那么这个棱柱的固定状态就由方程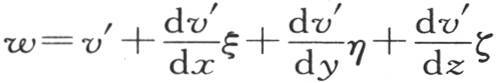 来表示。
来表示。
因此,与点m挨得无穷近的分子,在时刻t内,在状态变化着的这个固体中,和在状态为恒定的这个棱柱中,就有相同的有效温度。这样,在时刻dt内,过无穷小圆ω而存在于点m上的热流量,在这每一个固体中都相同;因此,它由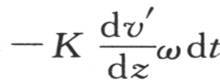 表示。
表示。
由此我们得到下述命题:
如果在内部温度根据分子的作用而随时间变化的一个固体中,我们引任一条直线,并在这条直线的不同点上作等于这些点在同一瞬间所得温度的一个平面曲线的纵坐标pm(见图5);那么,在这条直线的每一点p的热流量,与这条曲线元素和横坐标的平行线所成夹角α的正切成正比;即,如果我们把垂直于这条直线的一个无穷小圆ω的圆心放在点p上,那么,在时刻dt内,在横坐标op的延长线的方向上流过这个圆的热量,由四个因子的积来测定,这四个因子是,角α的正切,常系数K,圆面积ω,和时刻长度dt。
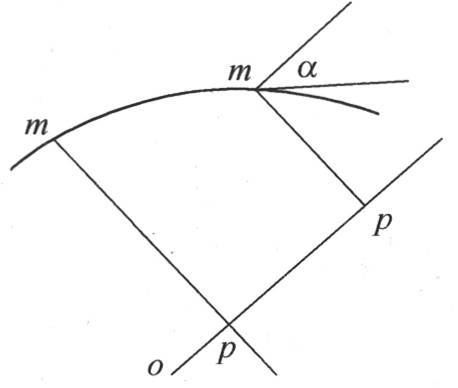
图5 【3】
141 推论. 如果我们用ε表示这条曲线的横坐标或者是这条直线的一点p与一个定点o的距离,用v表示代表点p的温度的纵坐标,那么,v随距离ε而变化,并且是这段距离的某个函数f(ε);流过位于点p并且与这条直线垂直的圆ω的热量,是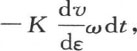 或者当用f′(ε)表示函数
或者当用f′(ε)表示函数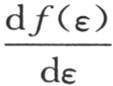 时,是-Kf′(ε)ωdt。
时,是-Kf′(ε)ωdt。
我们可以以便于应用的下述方式来表示这个结果。
为了得到在温度随分子的作用而变化的一个固体中所作的一条直线上一点p的有效热流量,我们应当用与点p挨得无穷近的两个点之间的距离除这两点的温差。这个热流量与这个商成正比。
142 定理4. 根据前面的定理,容易推出热传导的一般方程。
假定任一形状的一个同质固体的不同点已经得到由于分子相互作用的影响而连续变化的初始温度,假定方程v=f(x,y,z,t)表示这个固体的连续状态,那么,现在可以表明,一个有四个变量的函数v必然满足方程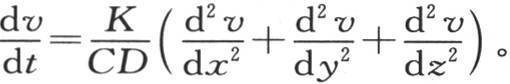
事实上,让我们考虑围在与x,y和z轴成直角的六个平面之间的一个分子的热运动;这些面的前三个经过坐标为x,y,z的点m,另外三个经过坐标为x+dx,y+dy,z+dz的点m′。
在时刻dt内,这个分子过经过点m的下矩形dx dy得到等于 的热量。为得到这个分子由对面所逃逸的热量,只需在前一表达式中把z变成z+dz,即把这个表达式仅对z所取的微分加到这个表达式本身中去就够了;这样,我们把
的热量。为得到这个分子由对面所逃逸的热量,只需在前一表达式中把z变成z+dz,即把这个表达式仅对z所取的微分加到这个表达式本身中去就够了;这样,我们把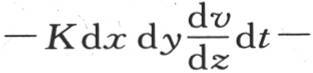
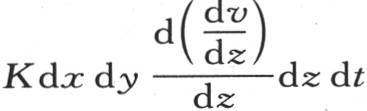 作为过上矩形所逃逸的热量的值。这同一分子也过经过点m的第一个矩形dz dx而得到等于
作为过上矩形所逃逸的热量的值。这同一分子也过经过点m的第一个矩形dz dx而得到等于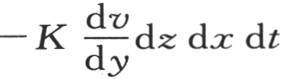 的热量;如果我们把它仅对y所取的微分加到这个表达式本身中去,则我们得到,过对面dz dx所逃逸的热量由
的热量;如果我们把它仅对y所取的微分加到这个表达式本身中去,则我们得到,过对面dz dx所逃逸的热量由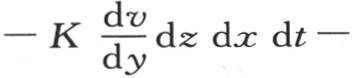
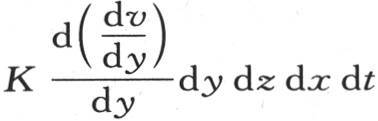 来表示。
来表示。
最后,这个分子经过第一个矩形dy dz而得到等于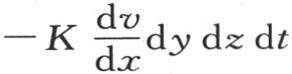 的热量,它过经过m′的对面的矩形所失去的热量由
的热量,它过经过m′的对面的矩形所失去的热量由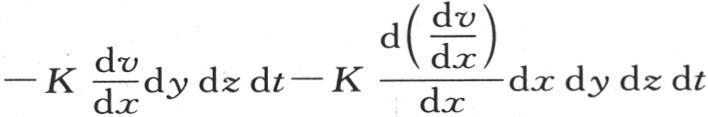 来表示。
来表示。
现在,我们应当取这个分子所得到的热量的和,并从中减去它所失去的热量的和。因此,在时刻dt内,聚积在这个分子内的总热量等于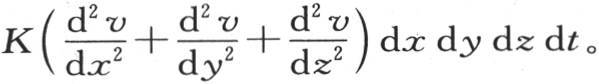 剩下的只是求由这个附加热所必然引起的温度的增量。
剩下的只是求由这个附加热所必然引起的温度的增量。
由于D是这个固体的密度或者是单位体积的重量,C是热容量或者是使单位重量从0度升至1度的热量;所以CDdx dy dz表示使体积为dx dy dz的这个分子从0度升至1度所需要的热量。所以,用这个积除这个分子所恰好得到的热量,我们就得到它的温度增量。因此,我们得到一般方程

它是所有固体内部的热传导方程。
143 与这个方程无关,这个温度系统常常受几个确定条件的支配,不可能给出这些条件的一般表达式,因为这些条件依赖于这个问题的性质。
如果热在其中传导的这个物体的体积有限,如果它的表面由于某个特殊原因保持一个给定的状态;例如,如果它所有的点由于那个原因保持恒定温度0,那么,用φ(x,y,z,t)表示未知函数v,我们就有条件方程φ(x,y,z,t)=0;无论t值如何,所有属于外表面的点x,y,z的值都肯定满足这个方程。此外,如果我们假定这个物体的初始温度由已知函数F(x,y,z)表示,那么,我们还有方程φ(x,y,z,0)=F(x,y,z);由这个方程所表示的条件肯定被属于这个固体的任一点的坐标x,y,z的所有值满足。
144 不用使这个物体的表面受恒温作用,我们可以代而假定这个表面的不同点的温度是不相同的,它依一条已知的规律随时间而变化;这条规律就是在地球温度问题中所发生的规律。在这种情况下,与表面有关的这个方程包含变量t。
145 为了从一个很一般的观点来单独考查热传导问题,我们应当假定初始状态被给定的这个固体的长、宽、高都是无穷的;这样,就没有任何特殊条件干扰热扩散了,这个原理所服从的规律就变得更明显;它由一般方程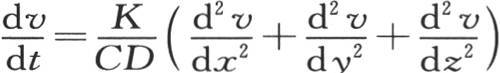 来表示,对于这个方程,我们应当加上与这个固体的任意初始状态有关的方程。
来表示,对于这个方程,我们应当加上与这个固体的任意初始状态有关的方程。
假定坐标为x,y,z的一个分子的初始温度是一个已知函数F(x,y,z),用φ(x,y,z)表示未知值v,我们有定义方程φ(x,y,z,0)=F(x,y,z);因此,这个问题以在时间为0时它可适合包含任意函数F的方程这样一种方式简化为一般方程(A)的积分。
第七节 与表面有关的一般方程
146 如果固体有一个确定的形状,如果它的初始温度被逐渐扩散到保持恒温的空气中,那么一般方程(A)和表示初始状态的方程就应当加上与表面状态有关的第三个条件。
在下面几目中,我们来考查表示这第三个条件的方程的性质。
考虑把热扩散到保持固定温度0度的空气中去的一个固体的变化状态。设ω是外表面的一个无穷小部分,μ是ω的一点,过这一点向这个表面作一条法线,这条线的不同点在同一时刻有不同的温度。
设v是点μ在一个确定时刻所得到的有效温度,w是这个固体在法线上一点ν所得到的相应的温度,点ν与点μ有一个无穷小量α的距离。用x,y,z表示点μ的坐标,点ν的坐标用x+δx,y+δy,z+δz来表示;设f(x,y,z)=0是适合于这个固体表面的一个已知方程,v=φ(x,y,z)是给出四变量函数ν的值的一般方程。对方程f(x,y,z)=0微分,我们有mdx+ndy+pdz=0;m,n,p是x,y,z的函数。
由第141目所阐明的推论得到,在法线方向上的热流量,或者说在面ω处在法线任一点上并且与法线垂直时在时刻dt内流过面ω的热量,与挨得无穷近的两个点的温差除以它们的距离所得的商成正比。所以,法线末端的这个热流量的表达式是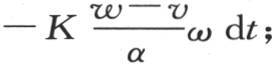 K表示这个物体的热导率。另一方面,面ω允许一定的热量逃逸到空气中去,在单位时间内,这个量等于hv ω dt;h是对应于空气的热导率。因此,法线末端的热流量有两个不同的表达式,即:hv ω dt和
K表示这个物体的热导率。另一方面,面ω允许一定的热量逃逸到空气中去,在单位时间内,这个量等于hv ω dt;h是对应于空气的热导率。因此,法线末端的热流量有两个不同的表达式,即:hv ω dt和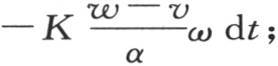 所以这两个量相等;与表面有关的条件正是通过这个等价性而被引入分析的。
所以这两个量相等;与表面有关的条件正是通过这个等价性而被引入分析的。
147 我们有 现在,由几何学的一些原理得到,坐标δx,δy,δz,它们确定与点μ所对应的法线上的点ν的位置,满足下面这些条件:pδx=mδz,pδy=nδz。
现在,由几何学的一些原理得到,坐标δx,δy,δz,它们确定与点μ所对应的法线上的点ν的位置,满足下面这些条件:pδx=mδz,pδy=nδz。
因此我们有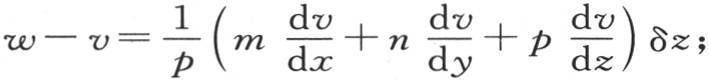 我们也有
我们也有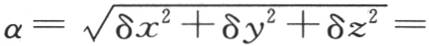
 或者是用q表示量
或者是用q表示量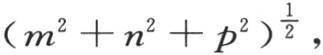 则有
则有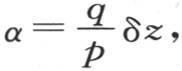 所以
所以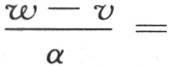
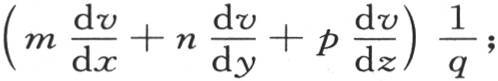 因此方程
因此方程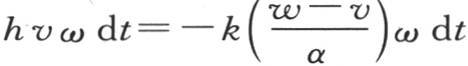 变成如下形式 【4】
变成如下形式 【4】
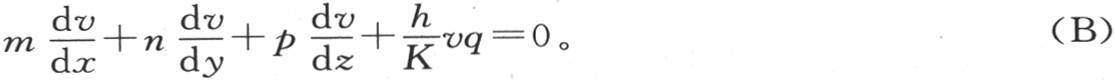
这个方程是确定的,并且只适用于表面上的点;它正是应当补充到热传导的一般方程(A)和确定这个固体初始状态的条件中去的方程;m,n,p,q是表面上的点的坐标的函数。
148 一般地,方程(B)表明在固体界面的法方向上的温降是这样进行的:因分子的作用而趋于逃逸的热量,总等于这个物体在介质中肯定会失去的热量。
我们可以设想这个固体物质以这样一种方式被延长:表面不是受空气的作用,而是属于它所界定的这个固体,同时也属于包含它的一个固体壳层的物体。在这个假定下,如果任一原因在每一时刻规定着这个固体壳层的温降,并且以方程(B)所表示的条件总被满足这样一种方式决定这种温降,那么,这个壳层的作用就代替空气的作用,并且热运动在这两种情况中相同:这样,我们可以假定这个原因存在,并且在这个假定下确定这个固体的变化状态;这就是在运用这两个方程(A)和(B)时所要做的。
由此可见,在使这个固体服从一个附加条件时,物体的中断和介质的作用怎样干扰热扩散。
149 我们也可以从另一种观点来考虑与表面状态有关的方程(B):不过,我们应当首先从定理3(第140目)推出一个值得注意的结论。我们保持同一定理的推论中所表示的结构(第141目)。设x,y,z是点p的坐标,x+δx,y+δy,z+δz是与点p挨得无穷近、并且取自所说的直线上一点q的坐标:如果我们用v和w表示这两点p和q在同一时刻所得到的温度,那么我们有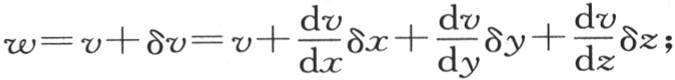 所以,商
所以,商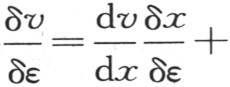
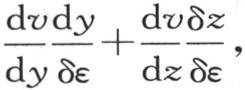 且
且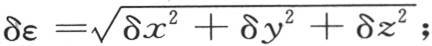 因此,流过位于点m并且与这条直线垂直的面ω的热量,是
因此,流过位于点m并且与这条直线垂直的面ω的热量,是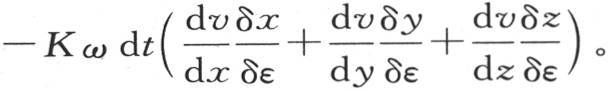
第一项是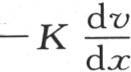 与dt和
与dt和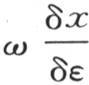 的积,根据几何原理,这后一个量是ω在y和z平面上的投影面积,如果这个投影面积在点p并且与x轴垂直,那么这个积就表示流过这个投影面积的热量。
的积,根据几何原理,这后一个量是ω在y和z平面上的投影面积,如果这个投影面积在点p并且与x轴垂直,那么这个积就表示流过这个投影面积的热量。
如果这个投影在点p并且与ω本身平行,那么,第二项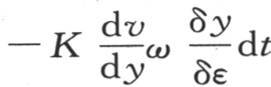 就表示经过在x和z平面上所作的ω的投影的热量。
就表示经过在x和z平面上所作的ω的投影的热量。
最后,如果这个投影在点p并且与纵坐标z垂直,那么第三项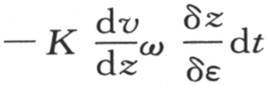 就表示在时刻dt内流过x和y平面上ω的投影的热量。
就表示在时刻dt内流过x和y平面上ω的投影的热量。
由此可见,流过在这个固体内部所作的一个面上的每个无穷小部分的热量,总可以分解成另外三个热流量,它们沿垂直于那些投影平面的方向而贯穿到这个面的三个正投影上。这个结果导致类似于在力的理论中所注意到的那些性质。
150 由于流过形状和位置已知的一个无穷小平面ω的热量等于经过它的三个正投影的热量,所以由此得到,如果我们设想固体内部一个任一形状的微元,那么从这个多面体的不同的面而进入其中的热量就相互补偿:更准确地说,进入由这个分子所得到的热量表达式的一阶项的和为零;因此,实际上聚积在这个分子中并且使其温度发生变化的热,只能由比那些一阶项无穷小的项来表示。
当一般方程(A)已经建立时,考虑一个棱柱形分子的热运动我们就可以明显地看到这个结果(第127和142目);用这个分子的三个投影所得到的热量代替过每个面所得到的热量,则这个论证可以扩展到任一形状的分子上去。
从其他方面来看也必然如此:因为,如果这个固体的某个分子在每一时刻内得到由一阶项所表示的热量,那么它的温度变化就比其他分子的变化无穷地大,即在每一无穷小时刻内,它的温度或者增加或者减少一个有限量,这与经验矛盾。
151 我们现在把这个注记运用到处在固体外表面的分子上去。
过在x和y平面上的一点a(见图6),作两个平面,一个与x轴垂直,另一个与y轴垂直。过这同一平面上与a挨得无穷近的点b,作与前两个平面平行的另外两个平面;从点a,b,c,d一直上升到固体外表面的纵坐标z,在外表面标出四个点a′,b′,c′,d′,并且成为其底为矩形abcd的棱柱的边。如果过表示四个点a′,b′,c′,d′的最小高度a′作一个平行于x和y平面的平面,那么它将从这个截棱柱上截下一个分子,这个分子的某个面,即a′b′c′d′,与这个固体的表面重合。四个纵坐标aa′,cc′,dd′,bb′的值如下:aa′=z,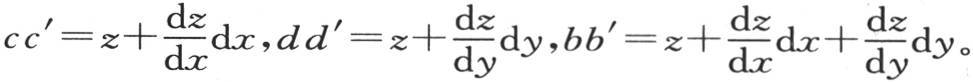
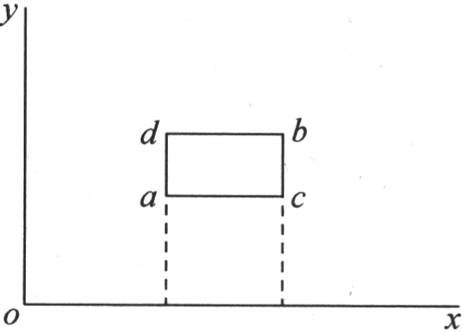
图6
152 垂直于x轴的某个面是一个三角形,其对面是一梯形。这个三角形的面积是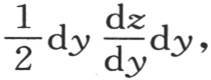 由于垂直于这个面的方向的热量是
由于垂直于这个面的方向的热量是 所以,忽略因子dt,我们把
所以,忽略因子dt,我们把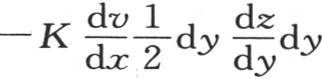 作为在某一时刻内过所说的这个三角形而进入这个分子的热量表达式。
作为在某一时刻内过所说的这个三角形而进入这个分子的热量表达式。
其对面的面积是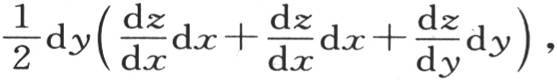 去掉比一阶项无穷小的二阶项,垂直于这个面的热流量也是
去掉比一阶项无穷小的二阶项,垂直于这个面的热流量也是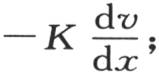 从经过第一个面而进入的热量中减去经过第二个面所逃逸的热量,我们得到
从经过第一个面而进入的热量中减去经过第二个面所逃逸的热量,我们得到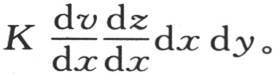
这个项表示这个分子通过垂直于x的两个面所得到的热量。
由一个类似的过程,我们可以得到这同一分子过垂直于y的两个面所得到的热量等于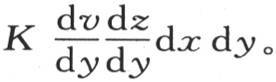
这个分子过矩形基底所得到的热量是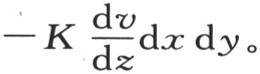 最后,过上表面a′b′c′d′有一定的热量逃逸掉,它等于进入那个外表面面积ω的积hv。根据已知的原理,ω的值与dx dy乘以比
最后,过上表面a′b′c′d′有一定的热量逃逸掉,它等于进入那个外表面面积ω的积hv。根据已知的原理,ω的值与dx dy乘以比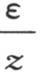 的值相同;ε表示外表面与x和y平面之间的法线长,且
的值相同;ε表示外表面与x和y平面之间的法线长,且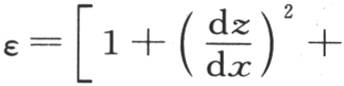
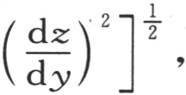 所以,这个分子过面a′b′c′d′失去等于
所以,这个分子过面a′b′c′d′失去等于 的热量。
的热量。
现在,为了使温度的变化在每一时刻不可能是一个有限量,进入由这个分子所得到的总热量的表达式的一阶项就应当相互抵消;这样,我们必定有方程
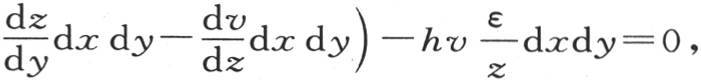 或者是
或者是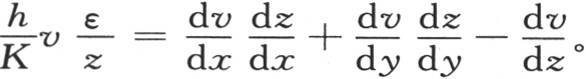
153 用由方程mdx+ndy+pdz=0所导出的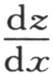 和
和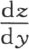 的值代替
的值代替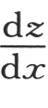 和
和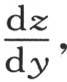 并且用q表示量
并且用q表示量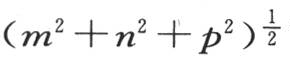 【5】 ,我们有
【5】 ,我们有
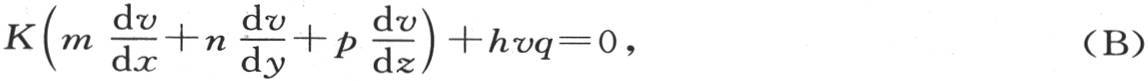
因此,我们显然知道由这个方程的每一项所表示的意义。
对所有这些项取异号,并且用dx dy来乘它们,则第一项表示这个分子过垂直于x的两个面得到多少热,第二项表示它过垂直于y的两个平面得到多少热,第三项表示它过垂直于z的面得到多少热,第四项表示它从介质那里得到多少热。因此,这个方程表示,所有一阶项的和为零,所得到的热只能由二阶项表示,而不能由别的项表示。
154 事实上,为了得到方程(B),我们把其基底在这个固体表面的一个分子看做是过它的不同的面而受热或失热的一个容器。这个方程表明,进入已经得到的热的表达式的所有一阶项相互抵消;因此热增益只能由二阶项表示。我们可以对这个分子赋予一个其轴与固体表面垂直的直棱柱的形状,或一个截棱柱的形状,或任一别的形状。
一般方程(A)(第142目)假定所有一阶项在这个物体内相互抵消,这对于被围在固体中的棱柱状分子是显然的。对于位于物体界面上的分子,方程(B)(第147目)表示同样的结果。
这些就是我们考查这一部分热理论的一般观点。
方程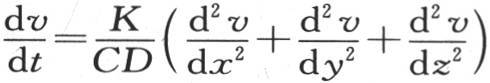 表示物体内部的热运动。它能使我们确定所有固体和液体物质每时每刻的分布,由此我们可以导出属于每一种特殊情况的方程。
表示物体内部的热运动。它能使我们确定所有固体和液体物质每时每刻的分布,由此我们可以导出属于每一种特殊情况的方程。
在下面两目中,我们将对圆柱和球的问题作出这种应用。
第八节 一般方程的应用
155 让我们用r表示任一圆柱形壳层的可变半径,如前面118目一样,假定所有与轴等距的分子在每一时刻有一共同的温度;v是r和t的函数;r是由方程r2 =y2 +z2 给定的y和z的函数。显然,首先v相对于x的变化为零;因此,项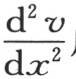 应当省略。这样,根据微分学的一些原理,我们有方程
应当省略。这样,根据微分学的一些原理,我们有方程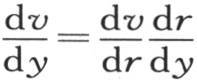 和
和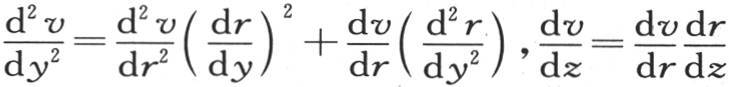 和
和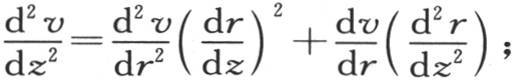 所以
所以
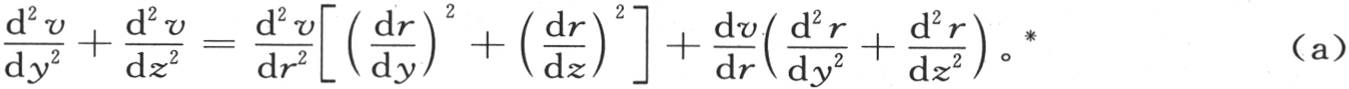
* 英文版中,方程(a)为: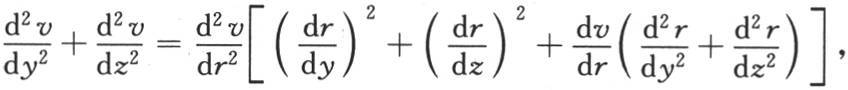 即大括号把等式右边
即大括号把等式右边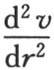 后的所有项都包含进去了,有误。现在的这个方程依法文《文集》版改正。——汉译者
后的所有项都包含进去了,有误。现在的这个方程依法文《文集》版改正。——汉译者
在这个方程的右边,量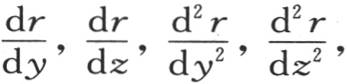 应当以它们各自的值来代替;为此,我们从方程y2 +z2 =r2 推出
应当以它们各自的值来代替;为此,我们从方程y2 +z2 =r2 推出 和
和 和
和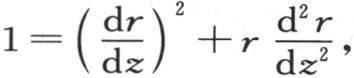 因此
因此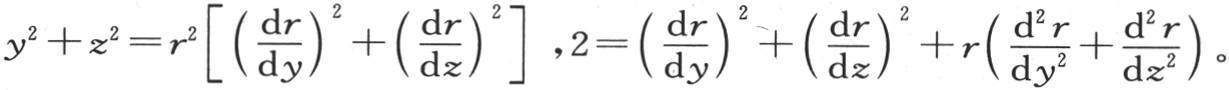 第一个方程的左边等于r2 ,所以它给出
第一个方程的左边等于r2 ,所以它给出

不用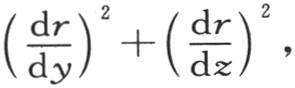 而取它的值1,则第二个方程给出
而取它的值1,则第二个方程给出

如果现在把方程(b)和(c)所给出的值代入(a),则我们有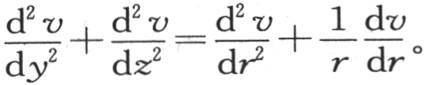 所以,正如在前面第119目所得到的,表示圆柱体中的热运动的方程是
所以,正如在前面第119目所得到的,表示圆柱体中的热运动的方程是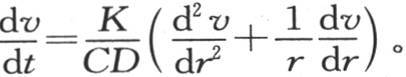
我们也可以假定与圆心等距的粒子没有得到相同的初始温度;在这种情况下,我们可以得到更一般得多的方程。
156 为了用方程(a)来确定已经浸没在一种液体中的一个球的热运动,我们把v看做是r和t的一个函数;由于r是壳层的可变半径,所以r是由方程r2 =x2 +y2 +z2 所给定的x,y,z的一个函数。这样,我们有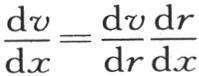 和
和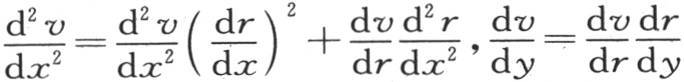 和
和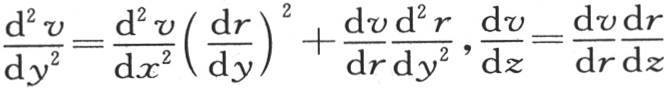 和
和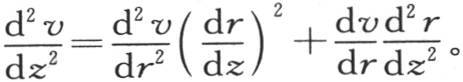
在方程 中作这些代换,则我们有
中作这些代换,则我们有
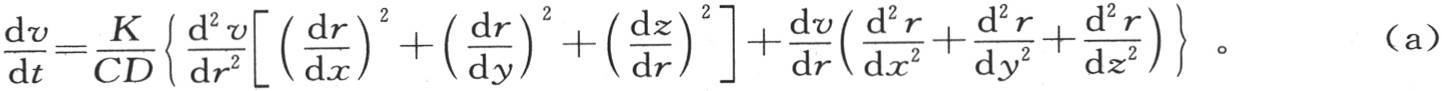
方程x2 +y2 +z2 =r2 给出下述结果;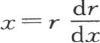 和
和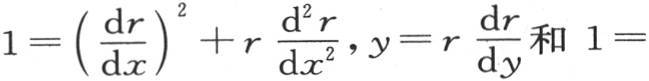

三个一阶方程给出: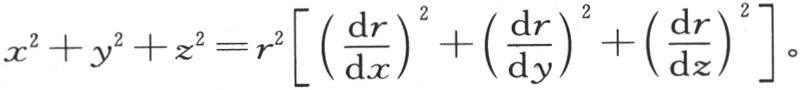
或者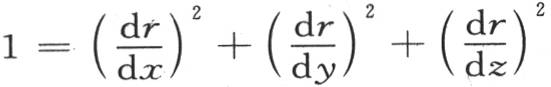 。 【6】
。 【6】
三个二阶方程给出: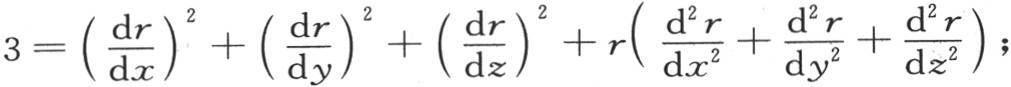 若不用
若不用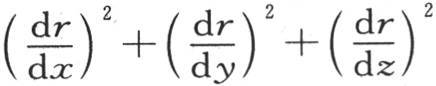 而取它的值1,则我们有
而取它的值1,则我们有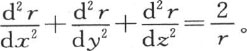
在方程(a)中作这些代换,我们有方程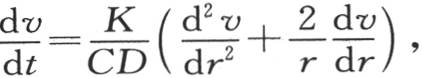 它与第114目中的方程相同。
它与第114目中的方程相同。
如果我们假定与球心等距的分子没有得到相同的初始温度,那么这个方程包含的项数就更多。
我们还可以从定义方程(B)推出在我们假定形状一定的固体向空气传热的特殊情况下,表示表面状态的方程;不过在大多数情况下,如果坐标选得恰当,这些方程就会立刻出现,并且它们的形式很简单。
第九节 一般注记
157 现在,固体中热运动规律的研究在于我们所建立的方程的积分;这是下面几章的事。我们对进入我们分析的那些量的性质给出几个一般的考虑,从而结束本章。
为了计量这些量并且用数值来表示它们,就应当使它们与不同的单位进行比较,这样的单位有五个,即长度单位,时间单位,温度单位,重量单位,最后是用于计量热量的单位。对于最后这个单位,我们本来可以选择使体积一定的某种物质从0度升至1度的热量。从许多方面看,选择这个单位,比选择使一个重量已知的冰块在0度时转变成相同物质的水而不使温度升高所需要的热量这样一种单位更好。我们采用后一种单位只是因为它在某种意义上已经在几本物理学的著作中早就被选定了;此外,这个假定可以使我们不用作任何改变而直接应用这些分析结果。
158 在每个物体中,确定热的可测作用的特殊要素总共有三个,即物体的固有热导率,对空气的热导率,以及热容量。表示这些量的数,和比重一样,是许多不同物质所特有的自然特征。
我们在第36目已经注意到,如果我们对真空中的辐射热的作用有更充分的观察,那么表面热导率就可能以更精确的方式测得。
正如在第一章第1节第11目所叙述的,我们可以看到,只有三个待定系数K,h,C进入这一研究;它们以观察来确定;我们将在最后指出可以精确测定它们的实验。
159 进入分析的数C,总是乘以密度D,即乘以等于单位体积重量的单位重量数;因此,积CD可以由系数c来代替。在这种情况下,我们应当把热容量理解为是使一种给定物质的单位体积,而不是那种物质的单位重量,从0度升至1度所需要的热量。
为了不违背通常的定义,我们曾认为热容量属于重量而非属于体积;然而,最好是用我们刚才所定义的系数c;这样,由单位重量所测定的数值就不进入分析式子了;我们要考虑的只是,第一,长度x,温度v,和时间t;第二,系数c,h,和K。前三个量是待定的,另外三个量对于每一种物质都是实验确定的常因素。至于单位面积和单位体积,它们不是绝对的,而取决于单位长度。
160 现在应当注意,每个待定量或者是常量都有本身固有的量纲(dimension),如果同一个方程的项没有相同的量纲指数(exponent of dimension),那么它们就不能比较。为了使我们的定义更精确,也为了检验这一分析,我们已经把这个考虑引入热理论。这个考虑来自关于量的基本概念;由于这个原因,它相当于希腊人未经证明而留给我们的基本引理。
161 在热的解析理论中,每个方程(E)都表示这些现存的量x,t,v,c,h,K之间的一种必然联系。这种联系决不依赖于长度单位的选择,从性质上看,长度单位的选择完全是偶然的,也就是说,如果我们用一个不同的单位测量长度,那么方程(E)仍然相同。于是,我们假定长度单位变了,并且它的第二个值等于第一个值除以m。在方程(E)中,表示某条线段ab,因而表示单位长度的某个倍数的任一个量x,对应于同一长度ab,就变成mx;时间值t和温度值v不变;特定因素h,K,c就不同了,第一个,h,变成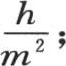 因为它表示在单位时间内从温度为1的单位面积所逃逸的热量。如果我们注意考察系数K的性质,那么正如我们在第68目和135目中曾经定义它的那样,我们会看出,它变成
因为它表示在单位时间内从温度为1的单位面积所逃逸的热量。如果我们注意考察系数K的性质,那么正如我们在第68目和135目中曾经定义它的那样,我们会看出,它变成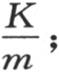 因为热流量与表面积成正比,与两个无穷平面之间的距离成反比(第72目)。至于表示积CD的系数c,它也取决于长度单位,并且变成
因为热流量与表面积成正比,与两个无穷平面之间的距离成反比(第72目)。至于表示积CD的系数c,它也取决于长度单位,并且变成 因此,当我们用mx代替x,同时用
因此,当我们用mx代替x,同时用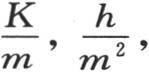
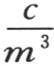 代替K,h,c时,方程(E)肯定不会发生任何变化;在作了这些代换之后,数m就消掉了:因此,x相对于长度单位的量纲是1,K的量纲是-1,h的量纲是-2,c的量纲是-3。如果我们把每个量本身的量纲指数赋予这各个量,那么这个方程是齐次的,因为每项都有相同的总指数。像S这样的一些数,它们表示面或者是立体,在第一种情况下是二维的,在第二种情况下,它是三维的。根据分析原理,角,正弦,以及其他三角函数,幂的对数和指数等,是不随长度单位而变化的绝对数(absolute numbers);因此,它们的量纲应当看做是0,这是所有绝对数的量纲。
代替K,h,c时,方程(E)肯定不会发生任何变化;在作了这些代换之后,数m就消掉了:因此,x相对于长度单位的量纲是1,K的量纲是-1,h的量纲是-2,c的量纲是-3。如果我们把每个量本身的量纲指数赋予这各个量,那么这个方程是齐次的,因为每项都有相同的总指数。像S这样的一些数,它们表示面或者是立体,在第一种情况下是二维的,在第二种情况下,它是三维的。根据分析原理,角,正弦,以及其他三角函数,幂的对数和指数等,是不随长度单位而变化的绝对数(absolute numbers);因此,它们的量纲应当看做是0,这是所有绝对数的量纲。
如果时间单位原来是1,现在变成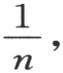 那么数t现在就变成nt,而数x和v不变。系数K,h,c则变成
那么数t现在就变成nt,而数x和v不变。系数K,h,c则变成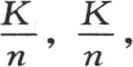 c。因此,x,t,v相对于时间单位的量纲是0,1,0;K,h,c的量纲是-1,-1,0。
c。因此,x,t,v相对于时间单位的量纲是0,1,0;K,h,c的量纲是-1,-1,0。
如果温度单位被改变,因而温度1变成对应于一种并非沸水效应的温度;并且如果那种效应需要更低的温度,这一温度相对于沸水温度是1比数p,那么,v就变成vp,x和t保持它们的值不变,系数K,h,c变成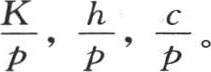
下表指明三个待定量和三个常量对于每种单位的量纲。
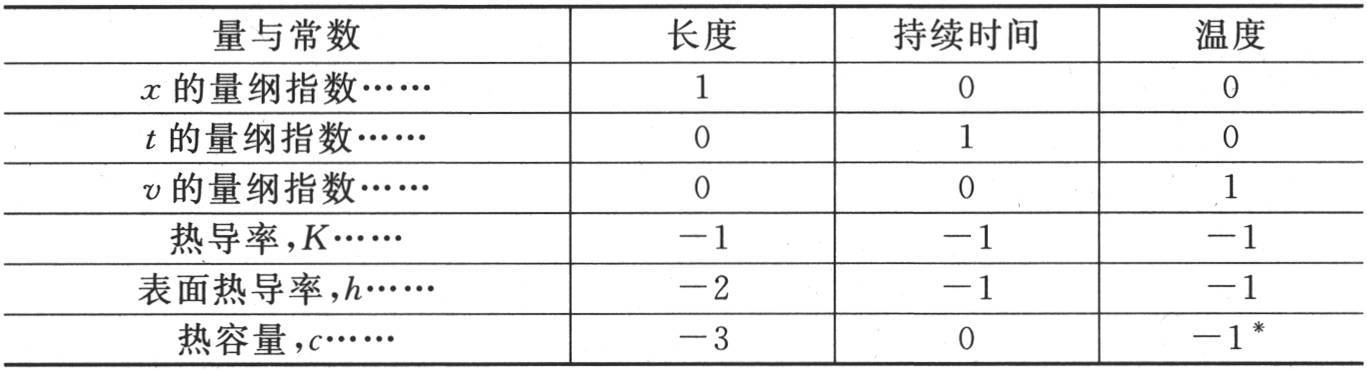
* 在英文本中,这里是1,有误。现根据法文《文集》本改正。——汉译者
162 如果我们保持系数C和D不动,它们的积曾由c来表示,那么,我们就不得不考虑重量单位,并且我们会得到,相对于长度单位,密度D的量纲指数是-3,C的量纲指数是0。
一但把上述规则运用到不同的方程和它们的变换上,我们就得到,它们相对于每种单位都是齐次的,每一个角量或者是指数量的量纲是零。如若不然,则要么是在分析中犯了错误,要么是引进了一些简化式。
例如,如果我们取第105目的方程(b),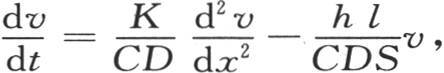 那么我们得到,相对于长度单位,这三项中每一项的量纲都是0;温度单位的量纲是1,时间单位的是-1。
那么我们得到,相对于长度单位,这三项中每一项的量纲都是0;温度单位的量纲是1,时间单位的是-1。
在第76目的方程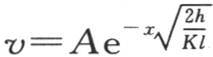 中,每一项的线性量纲是0。显然,无论长度单位和温度单位如何,指数
中,每一项的线性量纲是0。显然,无论长度单位和温度单位如何,指数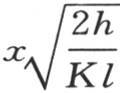 的量纲均为0。
的量纲均为0。
注释
【1】 除此处l表示面积为S的一个截面的周长外,这个方程与表示一端受热的一根有限长的棒的恒定温度的方程相同(第76目)。在这种有限长的棒的情况下,我们可以确定常数M和N之间的两个关系:因为,如果V是热源温度,在那里,x=0,则V=M+N;如果在这根棒远离热源的那一端,此时x=l,假定我们取与该端距离为dx的一个截面,那么,在单位时间内,过这个截面的热流量是 这与通过周边和这个薄片自由端的热耗散,即hv(ldx+S)相等;因此,最后当dx变为0时,
这与通过周边和这个薄片自由端的热耗散,即hv(ldx+S)相等;因此,最后当dx变为0时,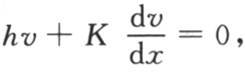 这时x=L,即
这时x=L,即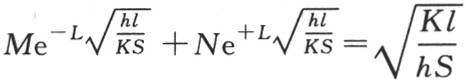
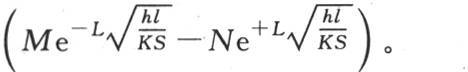
参见韦尔德,《物理演讲》,第37页。——A. F.
【2】 长度(length),看来在这里是指圆柱的高。——汉译者
【3】 在英文版中,图中的α是d,现根据法文《文集》本改定。——汉译者
【4】 设N是这条法线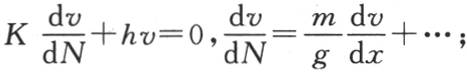 其余如原文。——R. L. E.
其余如原文。——R. L. E.
【5】 此式在英译本中为(m2 +n2 +p2 ),有误。现根据法文《文集》本改正。——汉译者
【6】 英文版没有这一行。这是根据法文《文集》版添加的。——汉译者
